\[ \def\read{\mathsf{read}} \def\write{\mathsf{write}} \def\reads{\mathsf{reads}} \def\writes{\mathsf{writes}} \def\Writes{\mathsf{Writes}} \def\SER{\mathsf{SER}} \def\SI{\mathsf{SI}} \def\PC{\mathsf{PC}} \def\CC{\mathsf{CC}} \def\RC{\mathsf{RC}} \def\RA{\mathsf{RA}} \def\po{\mathsf{\textcolor{red}{po}}} \def\so{\mathsf{\textcolor{purple}{so}}} \def\wr{\mathsf{\textcolor{teal}{wr}}} \def\ww{\mathsf{\textcolor{red}{ww}}} \def\rw{\mathsf{\textcolor{blue}{rw}}} \def\co{\mathsf{\textcolor{orange}{co}}} \def\SO{\mathsf{\textcolor{purple}{SO}}} \def\VIS{\mathsf{\textcolor{teal}{VIS}}} \def\antiVIS{\mathsf{\overline{\VIS^{-1}}}} \def\AR{\mathsf{\textcolor{orange}{AR}}} \def\CO{\mathsf{\textcolor{orange}{CO}}} \def\WR{\mathsf{\textcolor{teal}{WR}}} \def\WW{\mathsf{\textcolor{red}{WW}}} \def\RW{\mathsf{\textcolor{blue}{RW}}} \def\H{\mathcal{H}} \def\T{\mathcal{T}} \def\X{\mathcal{X}} \def\G{\mathcal{G}} \def\P{\mathcal{P}} \def\Int{\mathtt{Int}} \def\Ext{\mathtt{Ext}} \def\Session{\mathtt{Session}} \def\Prefix{\mathtt{Prefix}} \def\NoConflict{\mathtt{NoConflict}} \def\TotalVis{\mathtt{TotalVis}} \def\PreExecSI{\mathsf{PreExecSI}} \def\Executions{\mathsf{Executions}} \def\modelOf{\mathsf{modelOf}} \def\ExecSI{\mathsf{ExecSI}} \def\ExecSER{\mathsf{ExecSER}} \def\HistSI{\mathsf{HistSI}} \def\HistSER{\mathsf{HistSER}} \def\GraphSER{\mathsf{GraphSER}} \def\GraphSI{\mathsf{GraphSI}} \def\graph{\mathsf{graph}} \def\splice{\mathsf{splice}} \def\DCG{\mathsf{DCG}} \]
摘要
现代分布式系统通常依赖于所谓的弱一致性数据库,这种数据库通过削弱分布式事务处理的一致性保证来实现可扩展性。这种数据库的语义已被形式化为两种不同的风格,一种基于抽象执行,另一种基于依赖图。这两种风格的选择是根据预期应用做出的。前者用于指定和验证数据库的实现,而后者用于证明数据库客户端程序的属性。在本文中,我们提出了一组新的代数定律(不等式),将这两种规范风格联系起来。这些定律将基于抽象执行的规范中使用的二元关系与基于依赖图的规范中使用的二元关系联系起来。然后我们表明,这种代数联系产生了所谓的鲁棒性标准:确保弱一致性数据库的客户端程序不会因弱一致性而表现出异常行为的条件。这些标准使得推理这些客户端程序变得容易,并可能成为动态或静态程序分析的基础。对于某一类一致性模型规范,我们证明了连接两种规范风格的完整抽象结果。
作者:
- Andrea Cerone, IMDEA Software Institute
- Alexey Gotsman, IMDEA Software Institute
- Hongseok Yang, University of Oxford, UK
Introduction
现代分布式系统通常依赖于通过削弱分布式事务处理的一致性保证来实现可扩展性的数据库。这些数据库被认为实现了弱一致性模型。这种弱一致性数据库允许更快的事务处理,但会表现出异常行为,而这些行为在具有强一致性保证的数据库中不会出现,例如可序列化性。弱一致性数据库有两个重要问题:
- 找到其一致性模型的优雅形式规范,并证明这些规范已由数据库中使用的协议正确实现;
- 为在这些数据库上运行的应用程序开发有效的推理技术。
这些问题已经通过使用两种不同的形式化方法来解决,它们以不同的方式对弱一致性数据库的运行时行为进行建模。
当目标是验证实现弱一致性模型的协议的正确性时,分布式数据库的运行时行为通常用抽象执行 [13] 来描述,抽象执行抽象出了数据库的低级实现细节(第 2 节)。图 1 中的细边描述了一个抽象执行的示例。
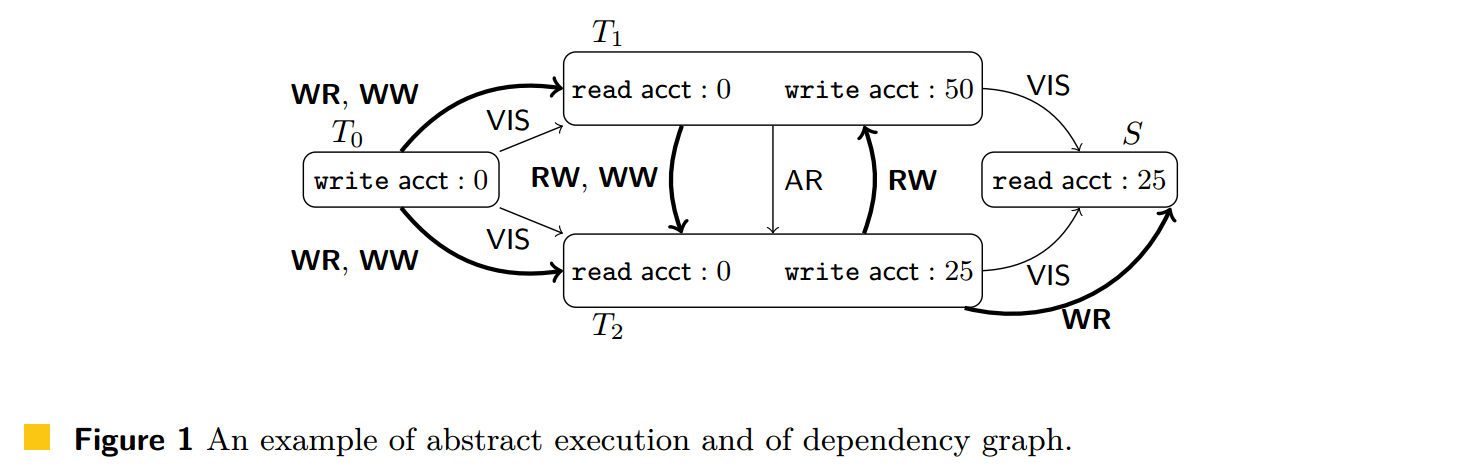
图 1 中的历史是不符合 SER 的,因为无法选择一个合适的 \(\VIS\),使得最终的抽象执行把 \(T_1, T_2\) 关联起来且结果的读操作和可见的更新一致。
使用抽象执行的一致性模型规范已被用于证明实现弱一致性模型的协议的正确性,以及证明这些模型的操作性和依赖于实现的描述[11, 12, 13, 15]。
另一种形式化方法使用依赖图来定义弱隔离级别,它已用于证明在弱一致性数据库上运行的客户端程序的属性。在图 4 中用粗边表示。
使用依赖图时,一致性模型被指定为事务集,其中存在满足某些属性的 \(\WR, \WW, \RW\) 关系,通常表述为非循环的特定关系 [7, 16];例如,可以通过要求依赖图是非循环的来指定可序列化性。由于事务的依赖关系在编译时可能被过度近似,因此依赖图方面的一致性模型规范已广泛用于手动或自动推理弱一致性数据库的客户端程序的属性 [19, 27]。它们还被用于验证一致性模型实现的复杂性和不可判定性结果 [9]。
我们的最终目标是揭示这两种指定弱一致性模型的风格之间的深层联系,这在文献中已暗示了特定的一致性模型。例如,这种联系将为我们提供一种系统的方法,从基于抽象执行的规范中推导出基于依赖图的弱一致性模型的规范,同时确保原始规范和派生规范在某种意义上是等价的。这样,即使数据库的一致性模型是根据抽象执行来指定的,我们也可以使用基于依赖图的技术 [9, 16, 18] 来证明弱一致性数据库的客户端程序的属性。
在本文中,我们介绍了朝着这一最终目标迈出的第一步。首先,我们观察到每个抽象执行都确定了一个底层依赖图。然后,我们在代数层面研究这两个结构之间的联系。我们提出了一组代数定律,这些定律在原始抽象执行所属的一致性模型的规范中是参数化的(第 4 节)。这些定律可用于推导形式为 \(R_G \subseteq R_A\) 的属性:这里 \(R_G\) 是来自带测试的 Kleene 代数 [22] 的表达式,其基本项是事务的运行时依赖关系,测试是事务的属性。关系 \(R_A\) 是抽象执行的基本关系之一:\(\VIS, \AR\) 或我们称之为反可见性的新关系 \(\antiVIS = \set{(T, S) \mid \lnot(S \xrightarrow{\VIS} T)}\)。我们提出的一些代数定律表明,每种依赖关系与抽象执行关系之间存在直接联系:\(\WR \subseteq \VIS, \WW \subseteq \AR, \RW \subseteq \antiVIS\)。其他定律捕捉了抽象执行关系 \(\VIS, \AR, \antiVIS\) 之间的联系。这种联系的确切性质取决于所考虑的抽象执行的一致性模型的规范。
我们特别感兴趣的是推导 \(R_G \subseteq \AR\) 形式的属性。这种形式的属性产生了所谓的客户端程序鲁棒性标准,这些条件确保程序即使在弱一致性模型下运行时也只表现出可序列化的行为 [7, 10, 19]。由于 \(\AR\) 是全序,这意味着 \(R_G\) 必须是无环的,因此所有环都必须是 \(R_G\) 的补集。然后我们可以在编译时检查是否存在此类关键环:由于可序列化数据库的依赖图始终是无环的,因此这确保了所述应用程序仅表现出可序列化的行为。
另一项贡献是,我们表明,对于相关的一类一致性模型,我们的代数定律可用于推导此类模型中的依赖图不仅必要而且充分的属性(第 5 节)。
Abstract Executions
定义 1
历史 \(\T = \set{T_1, T_2, \dots, T_n}\) 是事务的集合。
一致性模型 \(\Gamma\) 是客户端程序与数据库交互时可能出现的一组历史记录。为了正式定义 \(\Gamma\),我们用两个关系(称为可见性 \(\VIS\) 和仲裁 \(\AR\))来扩充历史记录。
定义 2
抽象执行 \(\X = (\T, \VIS, \AR)\)。其中 \(\VIS \subseteq \AR\),并且 \(\AR\) 是全序。
定义 3
抽象执行 \(\X = (\T, \VIS, \AR)\) 应该有 Last Write Win(LWW)性质,即若事务 \(T \ni (\read \ x : n)\),则集合 \(\T' = \set{\VIS^{-1}(T) \cap \Writes_x}\) 非空,且 \(\max_\AR (\T') \ni (\write \ x : n)\)。
定义 4
如果抽象执行 \(\X = (\T, \VIS, \AR)\) 中 \(\VIS\) 有传递性,则称该执行尊重因果(respect causality)。若抽象执行有 LWW 和尊重因果两种性质,则该执行是合法的(valid)。
除非另有说明,否则我们始终假设抽象执行是有效的。几个有趣的一致性模型允许的所有抽象执行都尊重因果关系。它们还简化了我们结果的数学发展。在 [17,附录 B] 中,我们解释了如何将我们的结果推广到不尊重因果关系的一致性模型。我们还讨论了如何将模型推广到考虑会话和会话保证 [29]。
我们可以分两步使用抽象执行来指定一致性模型。首先,我们确定抽象执行或公理的属性,这些属性正式表达了非正式的一致性保证,并形成一个满足属性的抽象执行集合。
接下来,我们将这个集合中的抽象执行投影到底层历史记录,并将一致性模型 \(\Gamma\) 定义为结果历史记录的集合。抽象执行隐藏了客户端程序和弱一致性数据库之间交互的低级操作细节。这一优势已被用于证明此类数据库实现了预期的一致性模型[11、12、13、15、20]。
Specification of Weak Consistency Models
在本节中,我们将介绍一个使用上面讨论的规范风格来指定一致性模型的简单框架。在我们的框架中,一致性模型的公理通过下面这种形式为的不等式将可见性和仲裁关系关联起来:
\[ R_1 ; AR_\X ; R_2 \subseteq VIS_\X \]
其中 \(R_1\) 和 \(R_2\) 是事务之间的特殊关系,\(\X\) 是抽象执行。正如我们稍后将解释的那样,这种形式的公理为抽象执行 X 中的两个事务通过 VISX 关联建立了必要条件,即它们不能同时执行。
尽管它很简单,但该框架具有足够的表达能力来捕获分布式数据库的几种一致性模型 [15, 23];正如我们将在第 4 节中展示的那样,这种简单性的好处之一是我们可以系统地推断一致性模型的鲁棒性标准。
正如我们将看到的,上述形式的公理中的关系 \(R_1, R_2\) 可能取决于抽象执行 \(\X\) 的可见性关系。为了定义这种关系,我们引入了规范函数的概念。
定义 5
函数 \(\rho : 2^{\mathbb{T} \times \mathbb{T}} \to 2^{\mathbb{T} \times \mathbb{T}}\) 是一个规范函数(specification function),若对于每个历史 \(\T\) 和关系 \(R \subseteq \T \times \T\),都有 \(\rho(R) = \rho(\T \times \T) \cap R?\)。其中 \(R?\) 是 \(R\) 的传递闭包。一致性保证(consistency guarantee),或者简称保证(guarantee),是一对规范函数 \((\rho、\pi)\)。
我们总是把规范函数应用到非传递性的关系上,尽管应用的结果是传递性的。
每个一致性保证 \((\rho, \pi)\) 定义了如下形式的公理:
\[ \rho(\VIS_\X) ; \AR_\X ; \pi(\VIS_\X) \subseteq \VIS_\X \]
若 \(\X\) 满足该公理,我们称其满足一致性保证 \((\rho, \pi)\)。一致性保证限制了 \(\X\) 中的两个事务 \(T, S\) 不能并发执行,即它们必须通过 \(\VIS_\X\) 边连接。根据定义,在抽象执行中 \(\VIS\) 边不能与 \(\AR\) 边相矛盾,因此,上述事务 \(T, S\) 的执行顺序自然由 \(\AR\) 决定:事实上,规范函数的定义确保了 \(\rho(\VIS_\X) \subseteq \VIS_\X?\) 和 \(\pi(\VIS_\X) \subseteq \VIS_\X?\) ,以便 \(\rho(\VIS_\X) ; \AR_\X ; \pi(\VIS_\X) \subseteq \AR_\X\) 对所有 \(\X\) 成立。
定义 6
一致性模型规范 \(\Sigma\) 或 x-specification 是一致性保证的集合 \(\set{(\rho_i, \pi_i)}_{i \in I}\),其中 \(I\) 是某个 index set(这是什么?)。
我们定义 \(\Executions(\Sigma)\) 为在 \(\Sigma\) 下所有合法的抽象执行的集合。令 \(\modelOf(\Sigma) := \set{\T_\X \mid \X \in \Executions(\Sigma)}\)。
Examples of Consistency Model Specifications
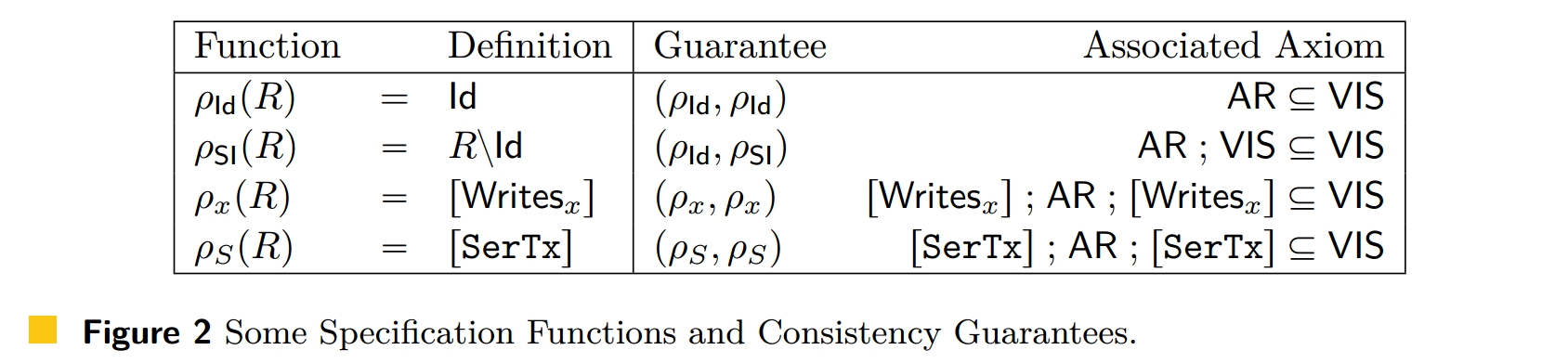
图 2 显示了规范函数和一致性保证的几个示例。在图中,我们使用关系 \([\T] := \set{(T, T) \mid T \in \T}, [o] := \set{(T, T) \mid T \ni o}\)。图中的保证可以组合在一起,以指定 [15] 中考虑的几个一致性模型:我们在下面给出了一些示例。这些一致性模型中的每一个都允许不同类型的异常:由于篇幅不足,这些在 [17,附录 A] 中进行了说明。
Causal Consistency
Red-Blue Consistency
Parallel Snapshot Isolation (PSI)
Snapshot Isolation (SI)
Serialisability
Dependency Graphs
我们提出了另一种基于依赖图的一致性模型规范样式,该样式在 [1] 中引入。这些结构捕获了访问同一对象的事务之间的数据依赖关系。此类依赖关系在编译时可能被过度近似。因此,它们已在针对在弱一致性模型下运行的程序的静态分析 [7、16、18、19] 中得到使用。
定义 7
依赖图 \(\G = (\T, \WR, \WW, \RW)\)。
Specification of Consistency Models using Dependency Graphs
Examples of g-specifications of consistency models.
Algebraic Laws for Weak Consistency
Weak Correspondence Problem
Strong Correspondence Problem
General Methodology
Presentation of the Laws
Applications
Characterisation of Simple Consistency Models
Characterisation of Simple x-specifications
Conclusion
我们在代数层面探索了两种不同风格弱一致性模型规范之间的联系。我们提出了几条定律,并应用这些定律设计了一致性模型的几个鲁棒性标准。据我们所知,这是第一个用于证明弱一致性模型鲁棒性的通用证明技术。我们已经证明,对于特定类别的一致性模型,我们的代数方法可以精确地用依赖图来描述一致性模型。
Related Work
Burckhardt 在 [12] 中引入了抽象执行,以模拟最终一致的数据存储的行为;它们已被用来捕获复制数据类型(Gotsman 等人 [13])、地理复制数据库(Cerone 等人 [15])和非事务性分布式存储系统(Viotti 等人 [30])的行为。
依赖图由 Adya [1] 引入;自那时起,它们就被用来推理在弱一致性模型下运行的程序。Bernardi 等人使用依赖图推导出几个一致性模型的稳健性标准 [7],包括 PSI 和红蓝;与我们的工作相比,其中包含的证明并不依赖于通用技术。Brutschy 等人将依赖图的概念推广到复制数据类型,并提出了最终一致性的稳健性标准 [10]。
弱一致性也出现在共享内存系统 [4] 的背景下。Alglave 等人在 [4] 中提出了用于指定弱内存模型的 CAT 语言,该语言还将弱内存模型指定为执行数据依赖关系上的一组非自反关系。Castellan [14] 和 Jeffrey 等人 [21] 提出了通过事件结构对弱内存模型进行不同形式化的方法。检查应用程序稳健性的问题也已在弱内存模型中得到解决 [2, 3, 8]。
Bouajjani 等人在 [9] 中也强调了强对应问题(第 5 节):作者强调需要通用技术来识别依赖图等结构中可能出现的所有不良模式。我们在 [16] 中解决了 SI 的强对应问题。

