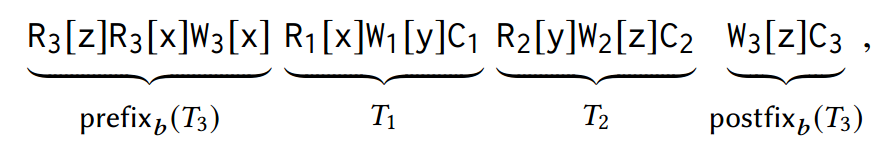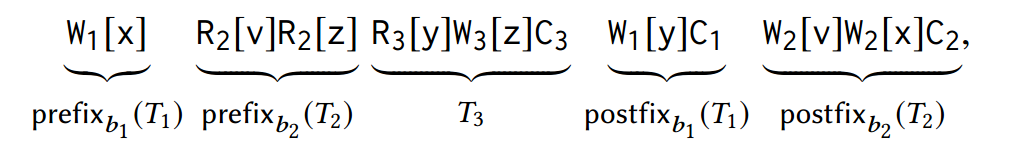\[ \def\Tuples{\mathbf} \def\ReadSet{\mathsf} \def\WriteSet{\mathsf} \def\prefix{\mathsf{prefix}} \def\postfix{\mathsf{postfix}} \def\pcfg{\textrm{prefix-confilct-free-graph}} \def\R{\mathsf{R}} \def\W{\mathsf{W}} \def\U{\mathsf{U}} \def\C{\mathsf{C}} \def\t{\mathsf{t}} \def\v{\mathsf{v}} \def\T{\mathcal{T}} \def\I{\mathcal{I}} \def\P{\mathcal{P}} \]
摘要
虽然可串行化始终保证应用程序的正确性,但可以选择较低的隔离级别来提高事务吞吐量,但风险是引入某些异常。如果在指定的隔离级别下,所有可能的事务交错都是可串行化的,则一组事务对给定的隔离级别具有鲁棒性。因此,鲁棒性始终保证应用程序的正确性,同时具有较低隔离级别的性能优势。虽然鲁棒性问题在文献中受到了广泛关注,但只获得了充分条件。最值得注意的例外是 Fekete 的开创性工作,他获得了确定针对 SI 的鲁棒性的特征。在本文中,我们解决了较低 SQL 隔离级别 RU 和 RC 的鲁棒性问题,它们是根据禁止的脏写和脏读模式定义的。本文的第一个主要贡献是,我们根据特定形式(拆分和多拆分调度 )的反例调度 的缺失以及满足各种属性的干涉图中的环的缺失来表征针对这两个隔离级别的鲁棒性。与 Fekete 的工作的一个关键区别是,本文获得的环属性必须考虑事务内操作的相对顺序,因为 RU 和 RC 不满足原子可见性要求。一个特殊的结果是后者导致了针对 RC coNP-complete 的鲁棒性问题。本文的第二个主要贡献是 coNP-hardness 证明。对于 RU,我们获得了 LOGSPACE-completeness。
作者:
- Bas Ketsman, Vrije Universiteit Brussel, Belgium
- Christoph Koch, École Polytechnique Fédérale de Lausanne, Switzerland
- Frank Neven, UHasselt, Data Science Institute, ACSL, Belgium
- Brecht Vandevoort, UHasselt, Data Science Institute, ACSL, Belgium
INTRODUCTION
为了保证事务并发执行期间的一致性,大多数数据库管理系统都提供可序列化的隔离级别。可序列化确保事务并发执行的效果始终等同于事务按顺序一个接一个地执行的串行执行。因此,数据库系统保证每个事务都具有完美的隔离性。对于应用程序程序员来说,完美的隔离性非常重要,因为这意味着他们只需要推断单个事务的正确性属性。然而,确保可序列化的代价是相当高的性能成本 [20]。因此,数据库系统通过提供各种隔离级别,提供了在隔离保证和性能提升之间进行权衡的能力。尽管通常默认配置了低于可序列化的隔离级别(例如,参见 [4]),但在这种隔离级别下并发执行事务并非没有风险,因为它可能会引入某些异常。然而,有时可以在低于可序列化的隔离级别下执行一组事务而不会引入任何异常。例如,在快照隔离下运行的 TPC-C 基准测试应用程序 [19] 就是这种情况。在这种情况下,事务集被认为对特定隔离级别具有鲁棒性。更正式地说,如果在指定隔离级别下允许的所有可能的事务交错都是可序列化的,则事务集对给定隔离级别具有鲁棒性。检测鲁棒性是非常可取的,因为它允许以较低隔离级别的性能为代价来保证完美的隔离。
Fekete 等人 [15] 在快照隔离的背景下发起了对稳健性的研究,将其称为可接受性问题,并提供了静态依赖图(我们和 Fekete [14] 称之为干涉图 interference graph)中不存在具有特定类型边的环的充分条件。 Bernardi 和 Gotsman [9] 扩展了这一结果,提供了充分条件来决定针对不同隔离级别的稳健性,这些隔离级别可以在 Cerone 等人 [10] 引入的声明性框架中定义。该框架提供了各种隔离级别(包括快照隔离)的统一规范,这些隔离级别允许原子可见性,该条件要求每个事务的所有更新对其他事务都可见或都不可见。原子可见性假设是关键,因为它允许通过事务级别上的一致性公理来指定隔离级别,而不是每个事务中各个操作的粒度。充分条件再次基于不存在具有某些类型边的环。
在一篇开创性的论文中,Fekete [14] 获得了一种用于确定针对快照隔离的稳健性的特征,这与上面提到的仅提供充分条件的工作形成了对比。在本文中,我们扩展了前者的工作,提供了针对较低 SQL 隔离级别( RU 和读取已提交)的稳健性特征,这些隔离级别是根据禁止脏写和脏读模式定义的 [8]。读取已提交是一种特别相关的隔离级别,因为它是相当多数据库系统的默认隔离级别 [5],也是为数不多的提供高可用性事务的隔离级别之一 [4]。此外,由于读取已提交以及扩展的 RU 提供的性能损失较低,建立针对这些隔离级别的稳健性可以实现快速并发执行,同时保证完美的隔离。Alomari 和 Fekete [3] 已经研究了针对读取已提交的稳健性,并提供了一个充分条件,但不是必要条件。
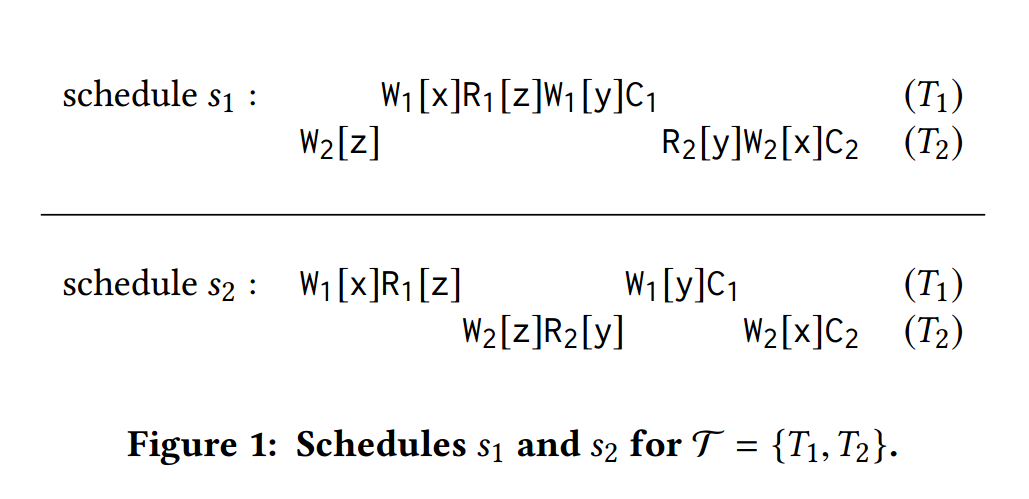
为了深入了解技术挑战,我们通过示例介绍了一些术语(正式定义在第 2 节中给出)。通常,事务是一系列对对象的读写操作,然后进行提交。例如,考虑事务集 T = {T1,T2},其中 T1 = W1[x]R1[z]W1[y]C1 和 T2 = W2[z]R2[y]W2[x]C2。这里,Wi[x] 和 Ri[x] 表示事务 Ti 对对象 x 的读写操作,而 Ci 是 Ti 的提交操作。那么,T 的调度就是 T 中事务中发生的所有操作的排序。例如,图 1 中显示的 s1 和 s2 是 T 的调度。当调度表现出脏写时,隔离级别 RU 下不允许执行调度:形式为 W1[x] · · · W2[x] · · · C1 的模式,即,T2 写入已被尚未提交的事务 T1 修改的对象。在 RU 下允许 s1 和 s2。隔离级别读取已提交禁止脏写和脏读。后者的形式为 W2[z] · · · R1[z] · · · C2。即,T1 读取已被尚未提交的事务 T2 修改的对象。在读取已提交下不允许调度 s1。请注意,s1 和 s2 不是冲突可序列化的,因为它们的冲突图允许环。事实上,考虑 s1,W2[z] 出现在 s1 中的 R1[z] 之前意味着在任何冲突中,等效顺序调度 T2 应该出现在 T1 之前,而 W1[x] 出现在 s1 中的 W2[x] 之前则意味着相反。
我们首先研究对 RU 的稳健性。这意味着对于给定的一组事务,我们需要检查是否存在一个反例调度,该调度在未提交读的情况下是允许的,并且不可序列化,即在其冲突图中包含一个环。请注意,对于上面定义的 T = {T1,T2},s1 构成了这样一个反例。此外,s1 的形式非常特殊。实际上,s1 可以看作是通过将 T2 拆分为两部分(W2[z] 和 R2[y]W2[x]C2)并将完整的事务 T1 置于两者之间而构建的调度。我们将此类调度称为拆分调度。它们也可以通过将一个事务拆分为两部分并将所有其他事务置于两者之间来定义由两个以上事务组成的事务集(参见图 2)。我们表明,具有拆分调度形式的反例调度的存在为决定对未提交读的稳健性提供了必要和充分条件。
Fekete [14] 引入了一组事务的干涉图概念,并获得了一种表征,该表征通过不存在具有某些类型边的环来确定对快照隔离的鲁棒性。我们模仿了他的结果,获得了另一种表征,该表征通过不存在前缀写冲突的干涉图中的环来确定对读未提交的鲁棒性。需要指出的是,它与 Fekete 的工作的主要区别在于:快照隔离承认原子可见性,这意味着干涉图中的环可以参考事务的全局顺序,并且可以忽略事务内操作的顺序。对于读未提交,我们不能依赖原子可见性,而需要考虑在干涉图中生成边的特定冲突操作。此外,前缀写入无冲突环的概念需要隔离单个事务(见证可转化性的事务,参见第 3 节以及将在反例调度 中拆分的事务)并确定此事务的前缀不存在写入冲突(因此操作顺序很重要)。话虽如此,由于我们表明它是 LOGSPACE-complete,因此可以非常有效地完成针对 RU 的稳健性的测试复杂性。
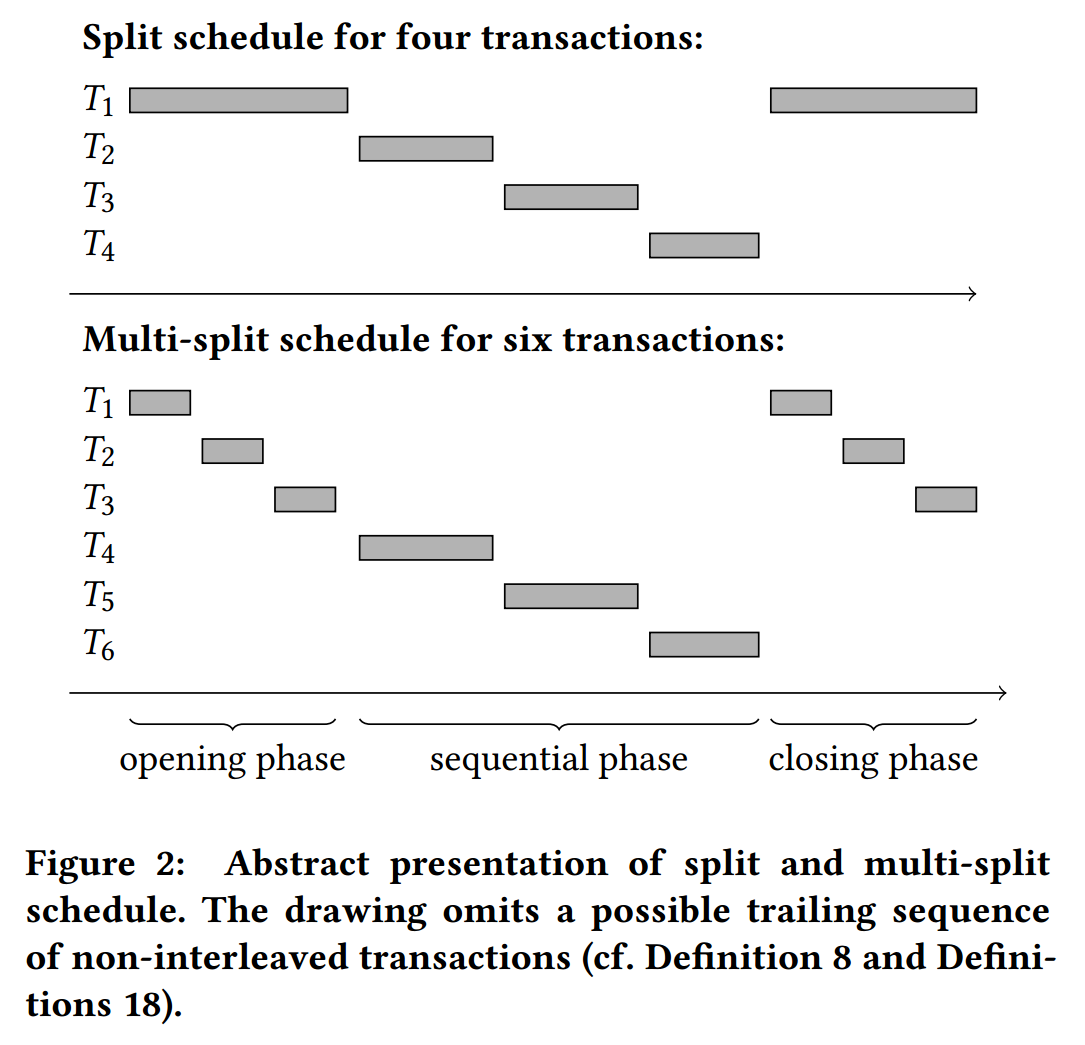
接下来,我们讨论对 RC 的稳健性。图 1 中所示的调度 s2 在 RC 下是允许的,并且不可序列化。因此,它是一个反例,表明 T 对读取已提交不稳健。请注意,s2 不是拆分调度。事实上,可以说,在读取已提交的情况下,T 不存在允许的拆分调度。这意味着以拆分调度形式存在的反例调度并不是决定对读取已提交的稳健性的必要条件。我们表明反例也不需要采用任意形式。我们获得了一个决定对读取已提交的稳健性的表征,其反例调度的形式为多拆分调度,如图 2 所示。与拆分调度(其中拆分一个事务并插入所有其他事务)相比,多拆分调度可以打开多个这样的事务,但需要按顺序关闭它们。
我们获得了干涉图中不存在多前缀无冲突环的等效特征。后者是环的一个相当复杂的属性,它比前面提到的前缀写无冲突概念更依赖于事务内操作的顺序。使用这个概念,我们表明决定对读取提交的鲁棒性是 conp-complete。下限证明是从 3SAT 中得出的一个相当复杂的简化,它与第 5.2 节中讨论的 ProperlyColoredCycle 问题的 np-hardness 证明中的思想有关。后者应该与对快照隔离的鲁棒性形成对比,[14] 中的算法暗示了 ptime 的上限。
继 Fekete [14] 的工作之后,我们首次获得了针对所考虑的隔离级别的鲁棒性的完整表征。本文的主要贡献可以总结如下:
- 提供针对 RU 和 RC(TODO:论文这里写错了)的鲁棒性判定表征,这些表征体现在不存在(i)各种形式的反例调度和(ii)各种形式的干涉图中的环;这些表征为判定鲁棒性的复杂性提供了直接的上限;
- 判定读取已提交的鲁棒性的复杂性。
概要。我们在第 2 节中介绍了必要的定义。我们在第 3 节中介绍了无隔离级别下的稳健性方面的关键概念。我们分别在第 4 节和第 5 节中考虑了针对读未提交和读已提交的稳健性。我们在第 6 节中讨论了相关工作,并在第 7 节中总结。
DEFINITIONS
Transactions and Schedules
Conflict Serializability
定义 1 冲突可串行化
如果调度 \(s\) 与串行调度冲突等价,则该调度是冲突可串行化的。
定理 2 [16] 冲突可串行化判定定理
当且仅当 \(s\) 的冲突图是无环的,则调度 \(s\) 是冲突可串行化的。
Isolation Levels
定义 3
如果调度没有表现出脏写,则允许在隔离级别 RU 下执行调度。在此之上,如果调度也没有表现出脏读,则允许在隔离级别 RC 下执行调度。为方便起见,我们使用术语“无隔离(no isolation)”来指代允许所有调度的隔离级别。
简言之,RU 不允许脏写,RC 不允许脏读和脏写。
Robustness
接下来,我们定义健壮性属性[9](在[14,15]中也称为可接受性),它保证在给定隔离级别下,给定一组事务的所有调度的可序列化性。
定义 4 鲁棒性
如果事务集 \(\T\) 在某个隔离级别下允许的每个调度都是冲突可序列化的,则该事务集 \(\T\) 对于该隔离级别是稳健的。
对于隔离级别 I,稳健性(I)是决定给定的一组事务 T 是否对 I 具有稳健性的问题。以下是直接的观察结果:
引理 5
假设 \(\T\) 为一组事务。假设 \(\I\) 和 \(\I'\) 为隔离级别,且 \(\I \subseteq \I'\)。则 \(\T\) 对 \(\I'\) 具有鲁棒性意味着 \(\T\) 对 \(\I\) 具有鲁棒性。
NO ISOLATION LEVEL
我们首先研究允许所有调度的无隔离隔离级别。本节作为本文其余部分的热身,并允许在简化的环境中讨论干涉图、可转化周期和拆分调度等关键概念。
我们使用 Fekete [14] 引入的干涉图的变体,它本质上将冲突图的概念从调度提升到事务集。与我们对冲突图的定义一致,我们通过显式标记边来揭示冲突操作。
定义 6 干涉图
对于一组事务 \(\T\),\(\T\) 的干涉图 \(IG(\T)\) 是这样的图,其节点为 \(\T\) 中的事务,并且如果 \(T_i\) 中的某个操作与 \(T_j\) 中的某个操作相冲突,则存在一条从 \(T_i\) 到 \(T_j\) 的边。同样,我们假设一个标记函数 \(\lambda\) 将每条边映射到一组冲突操作对。正式地说,\((b_i, a_j) \in \lambda(T_i,T_j)\) 当且仅当存在一个操作 \(b_i \in T_i\) 与操作 \(a_j \in T_j\) 相冲突。
显然,干涉图是无向图,或者说图中每条边都有对应的反向边。每个 \(CG(s)\) 都是 \(IG(\T)\) 的子图,前者的环也会出现在后者中。有时 \(IG(\T)\) 中的某个环不会在任何一个调度的冲突图中被翻译成相应的冲突环。因此我们要在干涉图中引入概念“可转化的环”,并在引理 10 中展示。当 \(IG(\T)\) 中有可转化的环时,一定存在一个拆分调度(定义 8)\(s\),该调度在 \(CG(s)\) 中允许一个环。
定义 7 可转化的环
事务集合 \(\T\),\(C\) 是 \(IG(\T)\) 中的一个环。若存在两条边 \((T_i, b_i, a_j, T_j), (T_j, b_j, a_k, T_k)\),其中 \(b_j \neq a_j\),则称 \(C\) 是非平凡的(non-trival)。进而,如果 \(b_j <_{T_j} a_j\),则称 \(C\) 是可转化(transferable)的。我们也称 \(C\) 在 \(T_j\) 中的操作 \((b_j, a_j)\) 上是可转化的。如果每个事务按照定义在一个环中恰好出现两次,则这个环是良定义的(well-defined)。若环中某个事务出现不止两次,则该环不是基本环,该环包括一个更小的基本环。
当环在 \(T\) 中的 \((b, a)\) 上可转化时,我们通过在 \(b\) 和 \(a\) 之间拆分 \(T\) 来创建拆分调度,将环中的所有其他事务插入到被创建的开头,同时保持它们的顺序,并在末尾以任意顺序附加未在环中发生的所有其他事务。请注意,拆分调度在其冲突图中显示一个环。拆分调度的正式定义如下:
定义 8 拆分调度
\(C\) 是 \(IG(\T)\) 中的一个可转化的环,\(\T\) 的一个基于 \(C\) 的拆分调度有如下的形式:
\[ \prefix_{b_1}(T_1) \cdot T_2 \cdot ... \cdot T_m \cdot \postfix_{b_1}(T_1) \cdot T_{m+1} \cdot ... \cdot T_n \]
其中,
- \((T_m, b_m, a, T_1), (T_1, b, a_2, T_2)\) 是 \(C\) 的一对边,并且 \(C\) 在 \(T\) 中的 \((b, a)\) 上是可转化的;
- \(T_1, \dots, T_m\) 是 \(C[T_1]\) 中的事务,且按顺序出现;
- \(T_{m+1} , \dots, T_n\) 是 \(\T\) 中剩余的事务,按照任意顺序排列。
更准确地说,我们称上述调度是对于 \(\T\) 的,在 \(C, T_1, b\) 上的一个拆分调度。
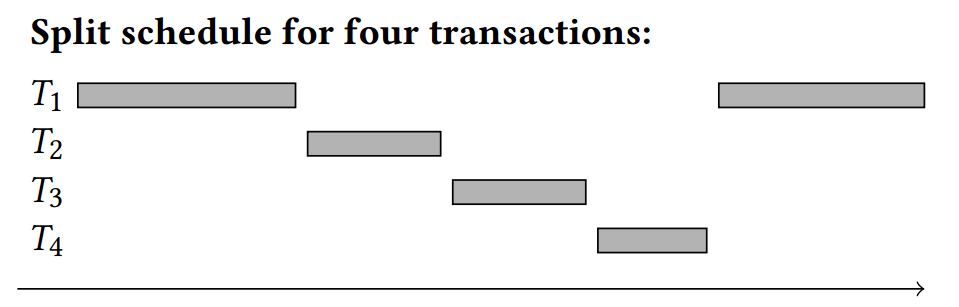
如果对于 \(\T\) 存在 \(IG(\T)\) 中的一个环 \(C\),使得 \(s\) 是 \(\T\) 的一个基于 \(C\) 的可拆分调度,则我们称 \(s\) 是 \(\T\) 的一个可拆分调度。图 2 提供了省略尾随序列 \(T_{m+1} \dots T_n\) 的拆分调度的抽象视图。
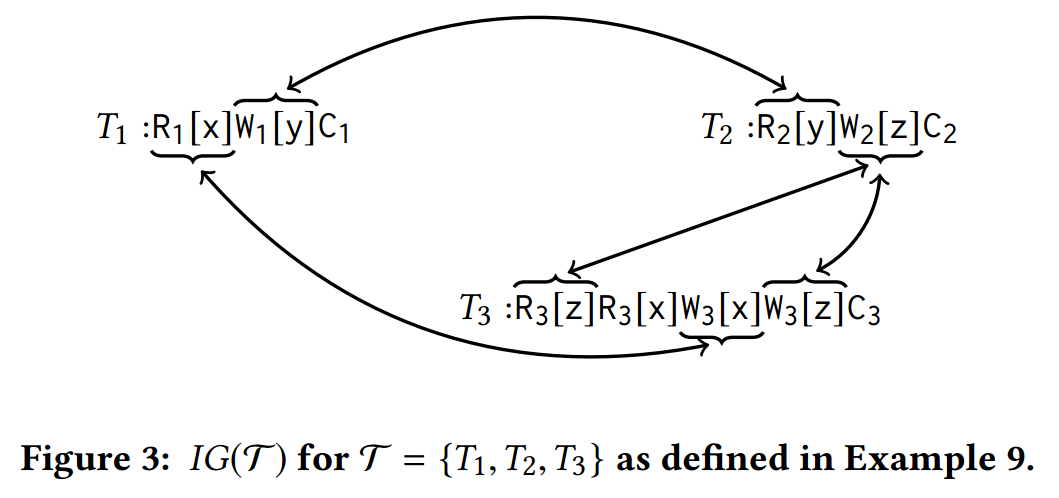
示例 9
如图 3 所示,\(C_1 = (T_1, \W_1[y], \R_2[y],T_2), (T_2, \W_2[z], \W_3[z],T_3), (T_3, \W_3[x], \R_1[x],T_1)\) 是一个可转化的环,而 \(C_2 = (T_1, \W_1[y], \R_2[y],T_2), (T_2, \W_2[z], \R_3[z],T_3), (T_3, \W_3[x], \R_1[x],T_1)\) 不是可转化的环。基于 \(C_1, T_3, \W_3[x]\) 的拆分调度 \(s_1\) 为:
其中,\(b = \W_3[x]\)。
下面的引理总结了事务的一些有趣的性质:
引理 10
对于事务集合 \(\T\):
- 若调度 \(s\) 的冲突图中有一个环 \(C\),则 \(C\) 在 \(IG(\T)\) 中是一个可转化的环;
- 若 \(IG(\T)\) 中存在一个非平凡的环 \(C\),则也存在一个可转化的环 \(C'\);
- 对于 \(\T\) 中一个基于 \(IG(\T)\) 中可转化环 \(C\) 的拆分调度 \(s\),\(C\) 是 \(CG(s)\) 中的一个环。
现在我们准备制定一个定理,该定理为确定无隔离的鲁棒性提供了特征:
引理 11 NI 下鲁棒性判定充要条件
事务集合 \(\T\) 对无隔离是不鲁棒的,当且仅当 \(IG(\T)\) 包含非平凡的环。
对于事务集合 \(\T\),下面的命题是等价的:
- \(\T\) 对无隔离不鲁棒;
- \(IG(\T)\) 包含非平凡的环;
- \(\T\) 存在拆分调度 \(s\)。
证明在论文原文,此处略。
接下来,我们讨论确定鲁棒性的复杂度。由于事务集 \(\T\) 的干涉图 \(IG(\T)\) 是双向的,因此它具有自然的无向解释。在下一个定理中,上限基于无向可达性在对数空间(logspace)中的结果 [17]。下限是通过 logspace-complete 全无向无环问题 [13] 的 fo-reduction(FO 应该是一阶谓词逻辑)得出的。
定理 12
鲁棒性(无隔离)是对数空间完全的。
READ UNCOMITTED
在本节中,我们讨论针对读取未提交的稳健性。这意味着反例调度不能再采用任意形式,而必须遵守读取未提交的隔离级别(在定义 3 中,RU 不允许脏写)。因此,除了干扰图中环的非平凡性之外,我们还需要其他要求。
不考虑导致这些冲突的具体操作的情况下,它们中发生的冲突类型。冲突类型包括事务之间的写-写、写-读和读写依赖关系。从这个角度来看,人们可能很容易认为,可以通过 \(IG(\T)\) 中不存在写-写冲突的可转化环来找到对抗读未提交的鲁棒性特征。但是,考虑 \(T = \set{\W_1[x]\R_1[y]\W_1[z]\C_1, \W_2[x]\R_2[z]\W_2[y]C2}\)。然后,有一个可转化环 \((T_1, \R_1[y], \W_2[y],T_2), (T_2, \R_2[z], \W_1[z],T_1)\),没有写-写冲突,但由于在 \(T_1\) 和 \(T_2\) 中都存在对 \(x\) 的前置写入,因此找不到在读未提交下允许的反例调度。此外,在读未提交下允许的调度的环仍然可能存在写-写冲突。实际上,由于没有脏写,所以允许在读取未提交的情况下执行调度 \(s_1 = \R_1[x]\W_2[x]\W_2[y]\C_2\W_1[y]\C_1\),但是 \(CG(s_1)\) 中的(唯一)环在 \(y\) 上存在写入-写入冲突。
为什么需要推理操作而不是事务的更高层次的解释是,隔离级别读未提交(和读已提交)不保证原子可见性,原子可见性要求每个事务的所有更新或者所有更新都对其他事务可见。更正式地说,事务集合 \(\T\) 上的调度 \(s\) 保证原子可见性,意味着对于所有的 \(T_i , T_j \in \T\),\(\W_i[x] <_s \R_j[x]\) 当且仅当 \(\W_i[y] <_s \R_j[y]\)。例如,调度 \(s_2 = \R_1[x]\R_2[y]\W_2[x]\W_2[y]\C_2\R_1[y]\C_1\) 在读未提交下是允许的,但不保证原子可见性,因为 \(\R_1[x] <_{s_2} \W_2[x]\) 而是 \(\W_2[y] <_{s_2} \R_1[y]\)。当隔离级别保证原子可见性时,只需在事务级别上推理,而不是在事务中发生的操作顺序上推理 [10]。对于读未提交(和读已提交),我们确实需要考虑各个事务中的操作顺序,这一点在接下来定义的前缀写冲突无环概念中将变得明显。
定义 13 无前缀写冲突
假设 \(\T\) 为一组事务,假设 \(C\) 为 \(IG(\T)\) 中的一个环。假设 \(T \in \T\) 且 \(b, a \in T\) 。那么,如果 \(C\) 在 \(T\) 上对操作 \((b, a)\) 是可转化的,并且 \(\prefix_b(T)\) 中不存在与 \(C \setminus \set{T}\) 中的事务中的写操作冲突(这里的冲突其实就是 ww 冲突,避免脏写)的写操作,则 \(C\) 在 \(T\) 上对操作 \((b, a)\) 是无前缀写冲突的(prefix-write-conflict-free)。
此外,如果对于某个 \(T \in \T\) 以及某些操作 \(b, a \in \T\) ,\(C\) 在 \(T\) 上的 \((b, a)\) 是无前缀写冲突的,则 \(C\) 是无前缀写冲突的。
示例 14
示例 9 中的环 \(C_1\) 在 \(T_3\) 中对操作 \((W3[x], W3[z])\) 不发生前缀写入冲突。实际上,在 \(T_2\) 或 \(T_1\) 中没有对对象 \(x\) 的写入操作。请注意,示例 9 中的拆分调度 \(s_1\) 在读取未提交的情况下是允许的。下一个引理表明情况总是如此。
引理 15
假设 \(\T\) 为一组事务。假设 \(C\) 为 \(IG(\T)\) 中的一个无前缀写冲突环。那么,存在一个基于 \(C\) 的 \(T\) 拆分调度,该调度在隔离级别 RU 下是允许的。
证明
发生脏写的唯一可能性是 \(\prefix_b(T)\) 中的写操作和 \(C\) 中不同于 \(T\) 的另一个事务的写操作都引用同一对象。由于 \(C\) 在 \(T\) 上的 \((b, a)\) 中无前缀写冲突,因此不可能出现这种情况。因此 \(s\) 符合 RU。
现在我们准备制定一个定理,该定理提供了一个特征,用于根据前缀写入无冲突环的存在来决定针对未提交读的鲁棒性。从引理 15 和引理 10(3) 很容易得出,前缀写入无冲突环的存在是反例调度存在的充分条件。下一个定理确定它也是一个必要条件,此外,总是可以找到一个以拆分调度形式出现的反例。
定理 16 RU 下鲁棒性判定充要条件
假设 \(\T\) 是一组事务。以下是等价的:
- \(\T\) 对隔离级别 RU 不具有鲁棒性;
- \(IG(\T)\) 包含一个无前缀写冲突环;
- 存在一个在 RU 下允许的 \(\T\) 的拆分调度 \(s\)。
READ COMITTED
接下来,我们讨论针对已提交读的稳健性,这意味着反例调度必须遵守已提交读的隔离级别。本节包含两个主要结果:
- 用多拆分调度和多前缀无冲突环来描述针对已提交读的稳健性(定理 23);
- 相关决策问题的复杂性(定理 27)。
Multi-split schedules

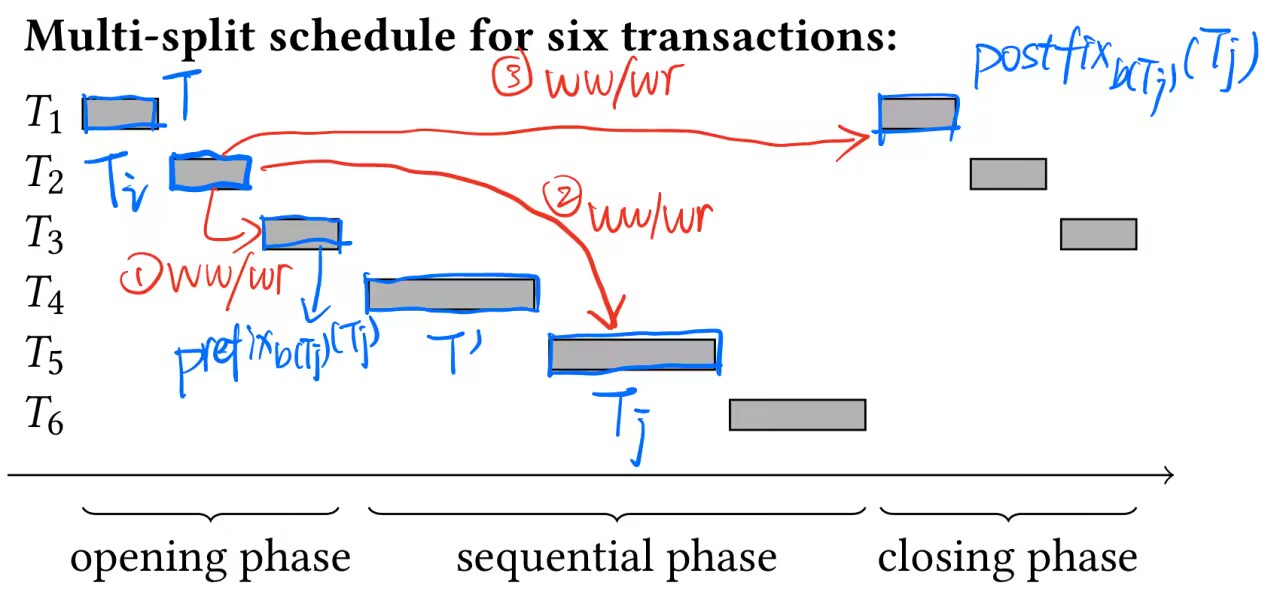
我们首先说明,当存在反例调度时,它始终可以采用基于可转化环的多拆分调度的形式,如下所定义。与拆分调度(其中拆分打开一项事务,并按照环中出现的顺序将所有其他事务插入其中)不同,多拆分调度可以打开环中连续出现的多项事务,但需要按顺序关闭它们。图 2 提供了拆分调度的抽象视图,其中省略了可能的非交错事务的尾随序列。为了便于定义多拆分调度,我们假设该调度所基于的环中的第一项事务是第一个打开的事务。
TODO:为什么要用多拆分调度代替拆分调度?
定义 18 多拆分调度
假设 \(\T\) 是一组事务,\(C\) 是 \(IG(\T)\) 中的一个环,该环在其第一个事务 \(T_1\) 中可在操作 \((b_1, a_1)\) 上转化。基于 \(C\) 的 \(T\) 多拆分调度是任何形式如下的调度
\[ \prefix_{\epsilon(T_1)}(T_1) \cdot ... \cdot \prefix_{\epsilon(T_m)}(T_m) \cdot \postfix_{\epsilon(T_1)}(T_1) \cdot ... \postfix_{\epsilon(T_m)}(T_m) \cdot T_{m+1} \cdot ... T_n \]
其中 \(T_1, \dots , T_m\) 表示 \(C\) 中按发生顺序排列的事务,\(T_{m+1}, \dots ,T_n\) 表示 \(\T\) 中按任意顺序排列的剩余事务。其中,\(\epsilon\) 是一个函数,它将 \(C\) 中发生的每个事务映射到其中的一个操作,并满足以下条件:对于每个 \(i > 1\):
- \(\epsilon(T_1) = b_1\) (\(T_1\) 打开);
- 若 \(\epsilon(T_{i-1}) = \C_{i-1}\),则 \(\epsilon(T_{i}) = \C_{i}\) (若上一个关闭,则这一个关闭);
- 若 \(\epsilon(T_{i-1}) \ne \C_{i-1}\),则 \(\epsilon(T_{i}) = b_i\) 或 \(\epsilon(T_{i}) = \C_{i}\) (若上一个打开,则这一个打开或关闭),且存在某个 \(j\),边 \((T_i, b_i, a_j, T_j)\) 在 \(C\) 中。
当 \(\epsilon(T_i) \ne \C_i\) 时,事务 \(T_i\) 称为打开,否则称为关闭。请注意,对于关闭的事务 \(T_i\) ,\(\prefix_{\epsilon(T_i)}(T_i) = T_i\) 且 \(\postfix_{\epsilon(T_i)}(T_i)\) 为空。当所有事务都打开时,多拆分调度完全拆分,即对于所有 \(i \in [1, m], \epsilon \in(T_i) \ne \C_i\)。
如果 \(s\) 是基于某个环 \(C\) 的 \(\T\) 多拆分调度,则我们称 \(s\) 为 \(\T\) 的多拆分调度。请注意,总有一个数字 \(k > 0\),使得 \(C\) 中发生的前 \(k\) 个事务打开状态,而其他事务(如果有)关闭。在完全拆分(fully split)调度中,没有已关闭的事务。
下一个引理证明,多拆分调度会在相应的冲突图中产生环。
引理 19
假设 \(s\) 是基于 \(IG(\T)\) 中的环 \(C\) 的事务集 \(\T\) 的多分裂调度。则 \(C\) 也是 \(CG(s)\) 中的一个环。
前面的引理并不意味着在读提交的情况下允许 \(s\)。为此,我们引入了多前缀无冲突环的定义。首先,我们定义以下概念。令 \(\T\) 为一组事务,\(C\) 为干扰图 \(IG(T)\) 中的环,\(T\) 为 \(\T\) 中的事务。那么对于某个 \(b \in T, T' \in \T, a \in T'\),\(C\) 中恰好存在一个形式为 \((T, b, a, T')\) 的边。为了便于表示,我们用 \(b_C(T)\) 表示 \(b\),用 \(a_C(T)\) 表示 \(a\)。当 \(C\) 从上下文中清楚时,我们还分别用 \(a(T)\) 和 \(b(T)\) 表示 \(a_C(T)\) 和 \(b_C(T)\)。
在以下定义中,\(T\) 和 \(T'\) 直观地指的是可以从多前缀无冲突环构造的多拆分调度中第一个打开的事务和最后一个打开的事务。
定义 20 无多前缀冲突
令 \(\T\) 为一组事务,令 \(C[T]\) 为 \(IG(\T)\) 中包含事务 \(T\) 和 \(T'\) 的一个环。则若 \(C\) 在 \(\T\) 中可转化,且对于 \(C[T]\) 中每个等于 \(T'\) 或在 \(T'\) 之前发生的事务 \(T_i\),不存在 \(\prefix_{b(T_i)}(T_i)\) 中的写操作,则 \(C\) 在 \(T\) 和 \(T'\) 中是无多前缀冲突(multi-prefix-conflict-free)的:
- 与 \(C[T]\) 中 \(T_i\) 之后但在 \(T'\) 之前或等于 \(T'\) 的某个事务 \(T_j\) 在 \(\prefix_{b(T_j)}(T_j)\) 中的读或写操作冲突(ww 或 wr 冲突);或,
- 与 \(C[T]\) 中 \(T'\) 之后发生的某个事务 \(T_j\) 的读或写操作冲突(ww 或 wr 冲突);或,
- 与 \(C[T]\) 中严格在 \(T_i\) 之前发生的某个事务 \(T_j\) 在 \(\postfix_{b(T_j)}(Tj)\) 中的读或写操作冲突(ww 或 wr 冲突)。
按照笔者的理解,其中这三条可以概括为“\(T_i\) 不能与其后的且在 \(T_i\) 关闭之前的块发生 ww 或 wr 冲突”,这是为看了避免脏读和脏写。
下图直观展示了三种不允许的冲突关系,使用红色箭头标注:
下一个引理表明,当可以找到一个无多前缀冲突的循环时,可以构造一个相应的反例多拆分调度,该调度见证了对读提交的非鲁棒性。在定理 23 中,我们证明了后者也是一个必要条件。
引理 21 多拆分调度
假设 \(\T\) 为一组事务。假设 \(C\) 为 \(IG(\T)\) 中的一个环,且该环在 \(T\) 和 \(T'\) 中无多前缀冲突。则存在一个 \(T\) 的基于 \(C\) 的多拆分调度,且该调度在隔离级别 RC 下是允许的。
示例 22
考虑 \(\T = \set{T_1, T_2, T_3}\),其中 \(T_1 = W_1[x]W_1[y]C_1, T_2 = \R_2[v]\R_2[z]\W_2[v]\W_2[x]\C_2, T_3 = \R_3[y]\W_3[z]\C_3\)。则 \(IG(\T)\) 如图 4 所示。由以下边 \((T_1, \W_1[x], \W_2[x],T_2), (T_2, \R_2[z], \W_3[z],T_3), (T_3, \R_3[y], \W_1[y],T_1)\) 组成的环 \(C\) 在 \(T_1\) 和 \(T_2\) 中无多前缀冲突。\(\T\) 的基于 \(C\) 的多拆分调度 \(s\)(其中 \(T_1\) 和 \(T_2\) 为开放状态,\(T_3\) 为封闭状态)如下所示:
其中 \(b_1 = \W_1[x]\) 且 \(b_2 = \R_2[z]\)。请注意,\(s\) 在 RC 的情况下是允许的。
在定理 23 的证明中,我们表明,任何见证对读取提交的非稳健性的反例调度都可以转换为多拆分调度。基本上,在多拆分调度中,每个事务都由一个或两个连续操作块表示。实际上,打开的事务由两个块表示,而关闭的事务以及尾随事务由一个块表示。我们将事务中的此类连续操作块称为块(chunk)。正式地,在 \(T\) 的调度 \(s\) 中,我们将来自同一事务 \(T\) 的极大连续操作序列称为 \(T\) 在 \(s\) 中的块。例如,在图 1 中,\(T_1\) 在 \(s_1\) 中由一个块(\(\W_1[x]\R_1[z]\W_1[y]\C_1\))表示,而 T2 由两个块(\(\W_2[z] 和 \R_2[y]\W_2[x]\C_2\))表示。
定理 23 RC 下鲁棒性判定充要条件
假设 \(\T\) 是一组事务。以下是等价的:
- \(\T\) 对隔离级别 RC 不具有鲁棒性;
- \(IG(\T)\) 包含一个无多前缀冲突循环;
- 存在一个 RC 允许的 \(\T\) 多拆分调度 \(s\)。
证明在论文原文,此处略。
Intermezzo: Properly colored cycles
在本节中,我们研究彩色图上的决策问题的复杂性。尽管该问题与决定鲁棒性没有直接关系,但我们提出的归约方法提供了简洁的直觉,这将是接下来第 5.3 节中介绍的更复杂的归约方法的核心。
conp-completeness
接下来,我们转到本节的主要结果,表明鲁棒性(RC)是 conp-complete。本节的其余部分致力于证明以下定理:
定理 27
鲁棒性(RC)是 conp-complete。
RA 及更强的隔离级别
挖掘鲁棒性充要条件的思想
\(\T\) 在某隔离级别 \(I\) 下不鲁棒 \(\iff\) \(I\) 下存在某个具有特性 D 的反例调度 \(s\) \(\iff\) \(s\) 符合特定限制 A 以满足 \(I\) \(\wedge\) \(CG(s)\) 中存在某个环 \(C\) 以违反 SER \(\iff\) \(s\) 符合特定限制 A 以满足 \(I\) \(\wedge\) \(IG(\T)\) 中存在符合特定限制 B的环 \(C\) \(\iff\) \(IG(\T)\) 中存在符合特定限制 C 的环 \(C\)
- “特定限制 A”与隔离级别 \(I\) 相关,以“XX 拆分调度”的形式给出
- “特定限制 B”与隔离击毙无关,被称为“可转化的环”
- “特定限制 C=A+B”由前两个限制共同决定,将“特定限制 A”从调度转化到 \(IG(\T)\) 上
\(\T\) 在 NI 下鲁棒 \(\Rightarrow\) \(\T\) 在 RU 下鲁棒 \(\Rightarrow\) \(\T\) 在 RC 下鲁棒 \(\Rightarrow\) \(\T\) 在更强隔离级别下鲁棒
\(\T\) 在更强隔离基本下不鲁棒 \(\Rightarrow\) \(\T\) 在 RC 下不鲁棒 \(\Rightarrow\) \(\T\) 在 RU 下不鲁棒 \(\Rightarrow\) \(\T\) 在 NI 下不鲁棒
隔离级别对比
本节内容来自:数据库事务发展史和 SSI 隔离级别原理。
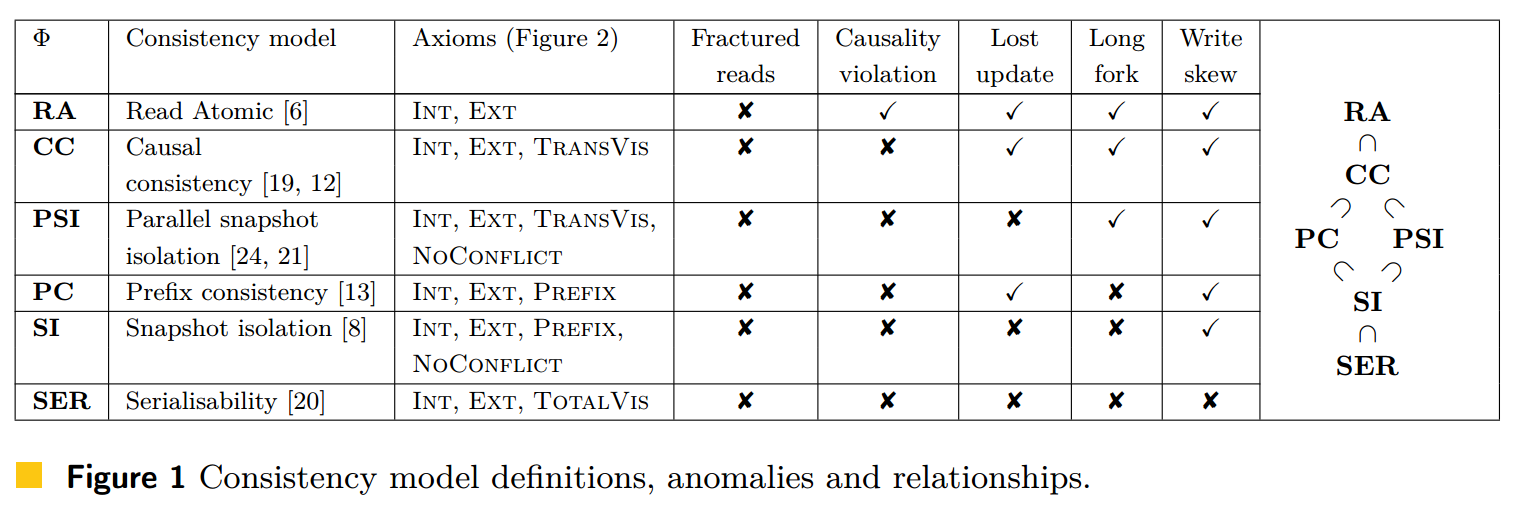
| Isolation Level(* for distributed) | P0 Dirty Write | P1 Dirty Read | P4 Lost Update | P2 Fuzzy Read | P3 Phantom | A5A Read Skew | A5B Write Skew |
|---|---|---|---|---|---|---|---|
| No Isolation | 允许 | 允许 | 允许 | 允许 | 允许 | 允许 | 允许 |
| Read Uncommitted | 不允许 | 允许 | 允许 | 允许 | 允许 | 允许 | 允许 |
| Read Comitted | 不允许 | 不允许 | 允许 | 允许 | 允许 | 允许 | 允许 |
| Repeatable Read (Read Atomic*) | 不允许 | 不允许 | 不允许 | 不允许 | 允许 | 不允许 | 允许 |
| Casual Consistency* | 不允许 | 不允许 | ? | 不允许 | ? | ? | 允许 |
| Parallel Snapshot Isolation* | |||||||
| Snapshot Isolation | 不允许 | 不允许 | 不允许 | 不允许 | 有时允许 | 不允许 | 允许 |
| Serializable | 不允许 | 不允许 | 不允许 | 不允许 | 不允许 | 不允许 | 不允许 |
不同隔离级别下不鲁棒充要条件对比
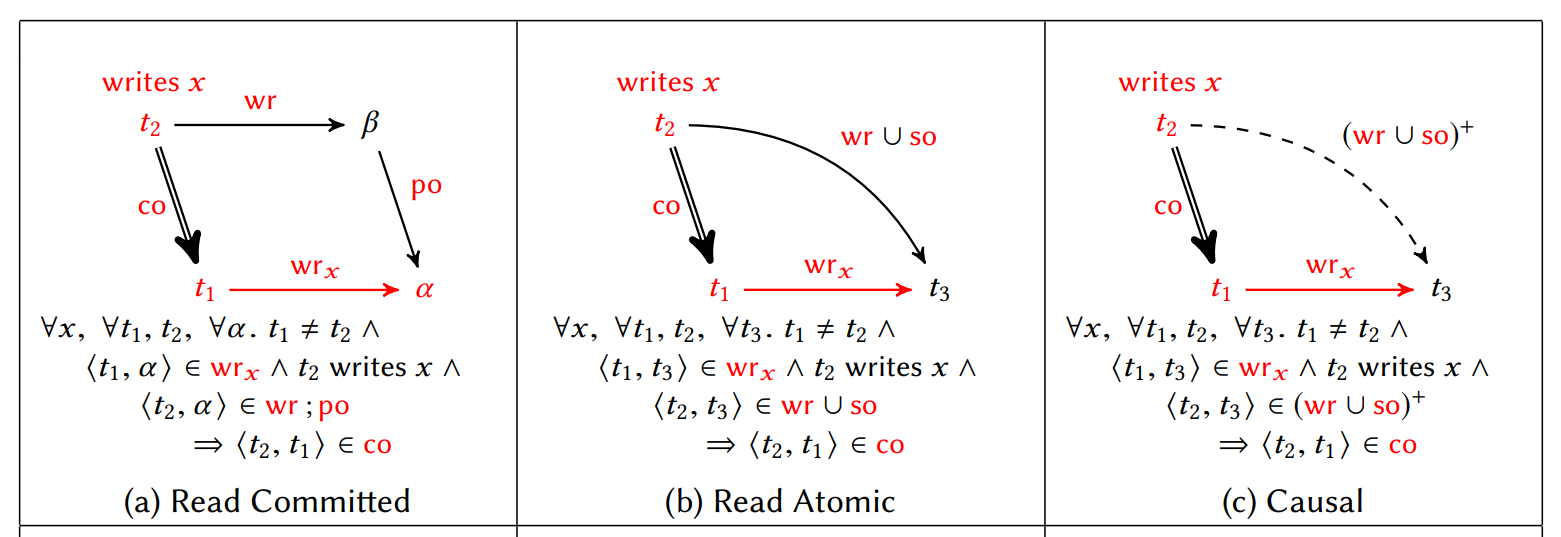
- NI、RU、RC 不支持原子可见性,因此需要在操作层面(而不是事务层面)进行推理;
- 对于支持原子可见性的隔离级别,只需要在事务层面推理;
- 相比于 RC,RA 不允许不可重复读(Non-Repeatable Read)异常:
\[ r1[x] \dots w2[x] \dots c2 \dots r1[x] \dots c1 \]
| 隔离级别 | 不允许的异常 | \(IG(\T)\) 中的环(限制 C) | 存在反例调度(特性 D) |
|---|---|---|---|
| NI | 无 | 非平凡环 | 拆分调度 |
| RU | 脏读 | 无前缀写冲突环 | RU 下允许的拆分调度 |
| RC | 脏写 | 无多前缀冲突循环 | RC 下允许的多拆分调度 |
| RA(如果有) | 不可重复读 | 更多限制的环 | 多拆分调度+禁止不可重复读 |
\(\T\) 在 NI 下鲁棒 \(\Rightarrow\) \(\T\) 在 RU 下鲁棒 \(\Rightarrow\) \(\T\) 在 RC 下鲁棒 \(\Rightarrow\) \(\T\) 在更强隔离基本下鲁棒
\(\T\) 在更强隔离基本下不鲁棒 \(\Rightarrow\) \(\T\) 在 RC 下不鲁棒 \(\Rightarrow\) \(\T\) 在 RU 下不鲁棒 \(\Rightarrow\) \(\T\) 在 NI 下不鲁棒
RELATED WORK
在本节中,我们讨论考虑鲁棒性问题(变体)的论文。
Sufficient conditions
Fekete 等人 [15] 通过扩展传统冲突图,添加关于每种冲突类型的额外信息,研究了快照隔离的稳健性问题。与我们的干扰图相比,这些静态依赖图仅捕获事务之间可能存在的冲突类型,而没有捕获导致这些冲突的具体操作。基于这些图,提出了针对快照隔离的稳健性的充分条件,以及在无法保证稳健性时如何修改事务的可能方法。Alomari 等人 [2] 研究了这些方法的性能。Alomari 和 Fekete [3] 提供了针对基于锁和多版本语义的读取提交的稳健性的充分条件。这项工作使用与 [15] 相同的图形方法。但是,提供的条件不是必要条件,因此不能用于表征针对读取提交的稳健性。
Cerone 等人 [10, CONCUR'15] 提供了一个框架,用于以声明方式统一指定不同的隔离级别。其框架中的一个关键假设是原子可见性,要求每个事务的所有更新对其他事务都是可见的,或者所有更新都对其他事务都是不可见的。此假设有助于对隔离级别进行推理,因为这些隔离级别可以通过事务级别的一致性公理来指定,而不是通过每个事务内的单个操作来指定。Bernardi 和 Gotsman [9] 扩展了 Fekete 等人 [15] 的工作,提供了针对此框架可定义的不同隔离级别的稳健性的充分条件。继续这项工作,Cerone、Gotsman 和 Yang [12] 研究了限制一组事务允许的调度的一致性公理与该组事务的静态依赖图中可能环的结果属性之间的关系。特别是,他们提供了一种更直接的方法,可以根据一致性公理指定的任意隔离级别从静态依赖图推导出稳健性标准。 Cerone 和 Gotsman [11] 后来改进了 Fekete 等人 [15] 首次获得的针对快照隔离的稳健性的充分条件。此外,他们还获得了针对快照隔离的针对并行快照隔离的稳健性的充分条件(即,对于给定的工作负载,在并行快照隔离下允许的每个调度是否在快照隔离下都允许)。但是,声明性框架是按事务级别而不是每个事务内的单个操作进行的。Bernardi 和 Gotsman [9] 扩展了 Fekete 等人 [15] 的工作,通过提供针对该框架可以定义的不同隔离级别的稳健性的充分条件。继续这项工作,Cerone、Gotsman 和 Yang [12] 研究了限制一组事务允许的调度的一致性公理与该组事务的静态依赖图中可能环的结果属性之间的关系。特别是,他们提供了一种更直接的方法,可以根据一致性公理指定的任意隔离级别从静态依赖图推导出稳健性标准。 Cerone 和 Gotsman [11] 后来改进了 Fekete 等人 [15] 首次获得的针对快照隔离的鲁棒性的充分条件。此外,他们还获得了针对快照隔离的针对并行快照隔离的鲁棒性的充分条件(即,对于给定的工作负载,在并行快照隔离下允许的每个调度是否在快照隔离下都允许)。然而,Cerone 等人 [10] 的声明性框架为上述工作提供了基础,但它不能用于研究 RC(因此 RU),因为它不承认原子可见性条件。
Characterizations
如前所述,Fekete [14] 是第一项提供必要和充分条件来决定对快照隔离的稳健性的工作。具体来说,这项工作为当每个事务在快照隔离或严格两相锁定 (S2PL) 下运行时的可接受分配提供了特征。当所有符合分配隔离级别的可能执行都是可序列化时,分配就是可接受的。作为附带结果,这项工作间接提供了对快照隔离的稳健性的必要和充分条件,因为当且仅当每个事务分配给快照隔离的分配是可接受的时,对快照隔离的稳健性才成立。
Beillahi 等人使用一种算法方法来决定对因果一致性 [7] 和快照隔离 [6] 的鲁棒性,方法是将这些问题简化为顺序一致共享内存上事务程序的可达性问题。他们的设置与我们的设置略有不同,因为它们允许事务的非确定性执行。此外,它们将事务分组到不同的进程下。在执行期间,每个进程依次但与其他进程同时运行其事务。由于这种不同的设置,他们获得的复杂性界限比我们的复杂性结果高得多。特别是,他们表明,决定对因果一致性和快照隔离的鲁棒性通常是 expspace-complete 的,如果站点数量或进程数量分别是固定的,则是 pspace-complete 的。
Transaction chopping
除了削弱隔离级别,事务还可以拆分成更小的部分以获得性能优势。然而,这种方法带来了新的挑战,因为这些切碎事务的每次可序列化执行不一定等同于原始事务的某些可序列化执行。如果对于切碎的每次可序列化执行,都存在原始事务的等效可序列化执行,则对一组事务的切碎是正确的。Shasha 等人 [18] 为这个正确性问题提供了基于图的表征。值得注意的是,对无隔离的稳健性对应于完全切碎事务的正确性。
事实上,如果我们将每个事务的每个操作切碎成自己的切碎事务,那么这种切碎的每个可序列化调度显然对应于无隔离下允许的原始事务的调度,反之亦然。然而,当考虑对读未提交和读已提交的稳健性时,这种关系不再是微不足道的。具体来说,我们不应该期望事务斩断正确性和针对读取提交的鲁棒性之间存在对应关系,因为前者是在多项式时间内可判定的[18],而我们证明了后者是 conp-complete。
CONCLUSIONS
在本文中,我们提供了针对隔离级别 RU 和读取已提交的稳健性的特征,并利用这些特征确定了相关决策问题复杂性的上限。我们还获得了匹配的下限。所获得的特征让我们深入了解了稳健性在这些设置中的含义以及在什么情况下会出现。
虽然本文中的特征不限于 SQL 隔离级别的传统基于锁的语义,因为它们是根据禁用模式 [8] 定义的,但看看在隔离级别的多版本定义 [1] 方面可以找到什么样的稳健性特征将会很有趣。第二个直接的问题涉及 conp-hardness 结果:是否存在使问题易于处理的自然限制。在具有数百万个事务的在线环境中,测试针对已提交读取的稳健性显然是不可行的,并且易于处理的限制或近似值是可取的。另一方面,在离线环境中,事务集是通过一组有限(且小)的事务程序生成的,如下所述,难处理性不一定是个问题。
研究稳健性的最初动机在于通过在较弱的隔离级别执行事务而获得的性能改进,而不会引入异常的危险 [15]。需要指出的是,稳健性在可以将事务分组在一起或事先知道可能的事务集的设置中最有意义。后者的自然发生是当事务由一组有限的参数化事务程序生成时,例如在银行应用程序中,客户可以进行固定数量的金融事务。考虑参数化事务 \(\tau = R[v]W[v]R[w]R[w]\),它表示从帐户 \(v\) 到帐户 \(w\) 的转账,其中 \(v\) 和 \(w\) 是变量。任何事务 \(T = R[x]W[x]R[y]R[y]\) 其中 \(x, y \in \Obj\) 都是 \(\tau\) 的一个实例。对于这个例子,用同一个对象 \(x\) 来解释 \(v\) 和 \(w\) 甚至是有意义的。然而,在某些情况下,不允许同一个对象解释不同的变量是有意义的。在未来的工作中,我们将研究参数化事务形式化的鲁棒性问题。在这样的设置中,相同的特征仍然成立,但干涉图变得无限大。初步结果表明,根据特定强制不相交变量域约束,可以获得与本文相同的鲁棒性复杂性。
稳健性是一个二元属性:一组事务在给定的隔离级别下是稳健的,或者不是。当不具备稳健性时,可以设计方法使一组事务变得稳健,或者将事务拆分为最大程度稳健的子集。这些问题已在快照隔离中考虑过 [11, 15],考虑数据库系统中出现的不同隔离级别是有意义的 [4]。一个正交的、无疑更具挑战性的设置是脱离每个事务都必须在同一隔离级别执行的要求。也就是说,对于给定的一组事务程序,将每个事务分配给最佳隔离级别以获得合适的优化概念。对最优性的直接解释可能是每个事务的尽可能弱的隔离级别,以保证整个集合的整体稳健性。Fekete [14] 研究并解决了快照隔离和严格两相锁定的分配问题,但对于其他隔离级别没有得到这种结果。