$$ \def\P{\mathcal{P}} \def\Tr{\mathsf{Tr}} \def\PO{\mathsf{\textcolor{black}{PO}}} \def\WR{\mathsf{\textcolor{green}{WR}}} \def\WW{\mathsf{\textcolor{red}{WW}}} \def\RW{\mathsf{\textcolor{blue}{RW}}} \def\CO{\mathsf{\textcolor{orange}{CO}}} \def\ARB{\mathsf{\textcolor{pink}{ARB}}} \def\CC{\mathtt{CC}} \def\PC{\mathtt{PC}} \def\SI{\mathtt{SI}} \def\SER{\mathtt{SER}} \def\assume{\mathtt{assume}} \def\CountTickets{\mathtt{CountTickets}} \def\Register{\mathtt{Register}} \def\CreateEvent{\mathtt{CreateEvent}} \def\assume{\mathtt{assume}} \def\Password{\mathtt{Password}} \def\AxPrefix{\mathsf{AxPrefix}} $$
摘要
对数据库的并发访问通常封装在事务中,以便与其他并发计算隔离并具有对故障的恢复能力。现代数据库为事务提供了各种语义,这些语义对应于一致性和可用性之间的不同权衡。由于较弱的一致性模型提供了更好的性能,因此一个重要的问题是研究给定程序所需的最弱一致性级别(以满足其规范)。作为处理此问题的一种方法,我们研究了在用较弱的一致性模型替换一致性模型时检查给定程序是否具有相同的行为集的问题。这种称为鲁棒性的属性通常意味着在削弱一致性时程序的任何规范都会得到保留。我们专注于比标准可序列化性更弱的一致性模型的鲁棒性问题,即因果一致性、前缀一致性和快照隔离。我们表明,检查这些模型之间的鲁棒性是多项式时间可归结为可序列化下的状态可达性问题。我们还使用这种归结来推导一种基于 Lipton 归结理论的实用证明技术,该技术可以证明程序是鲁棒的。我们已经将我们的技术应用于分布式系统和数据库文献中的几个具有挑战性的应用。
作者:
- Sidi Mohamed Beillahi, Université de Paris, IRIF, CNRS, F-75013 Paris, France
- Ahmed Bouajjani, Université de Paris, IRIF, CNRS, F-75013 Paris, France
- Constantin Enea, Université de Paris, IRIF, CNRS, F-75013 Paris, France
Introduction
对数据库的并发访问通常封装在事务中,以便与其他并发计算隔离并具有故障恢复能力。现代数据库为事务提供了各种语义,对应于一致性和可用性之间的不同权衡。最强的一致性级别是通过可序列化事务 [42] 实现的,其并发执行的结果与事务按某种顺序原子执行的结果相同。由于可序列化(SER)会严重损害可用性,现代数据库通常提供较弱的一致性模型,例如因果一致性(CC)[38]、前缀一致性(PC)[22, 25] 和快照隔离(SI)[12]。因果一致性要求,如果事务 $t_1$“影响”另一个事务 $t_2$,例如,$t_1$ 在同一会话中在 $t_2$ 之前执行,或者 $t_2$ 读取了 $t_1$ 写入的值,则这两个事务中的更新可以被按此顺序的任何其他事务观察到。并发事务彼此之间没有因果关系,因此可以以不同的顺序观察到这些事务,从而导致 SER 下不可能出现的行为。前缀一致性要求所有事务之间存在一个总提交顺序,以便每个事务都能观察到此序列前缀中的所有更新(PC 强于 CC)。两个事务可以观察到相同的前缀,从而导致 SER 不允许的行为。快照隔离进一步要求,如果两个不同的事务都写入一个公共变量,则它们会观察到不同的前缀。
由于较弱的一致性模型提供了更好的性能,因此一个重要的问题是确定程序所需的最弱一致性级别(以满足其规范)。解决这个问题的一种方法是检查在一致性模型 S 下设计的程序 $\P$ 在较弱的一致性模型 W 下运行时是否具有相同的行为。程序的这种属性通常被称为对用 W 替换 S 的鲁棒性。这意味着在削弱一致性模型(从 S 到 W)时,$\P$ 的任何规范都会得到保留。保留任何规范都很方便,因为规范在实践中很少出现。
最近的几篇论文研究了检查给定程序的鲁棒性问题,但仅限于强模型(S)为 SER 的情况,例如 [9, 10, 19, 26, 13, 40],或非事务情况下的顺序一致性的情况,例如 [36, 15, 29]。然而,即使在存在“异常”的情况下,即 SER 不允许的行为,也有一大类规范可以实现(有关讨论,请参阅 [46])。在这种情况下,一个重要的问题是,某个实现(程序)是否能够抵御用把弱一致性模型(例如 SI)替换为更弱的模型(例如 CC)的鲁棒性。
在本文中,我们考虑了上述越来越强的一致性模型序列,即 CC、PC 和 SI,并研究了检查给定程序的鲁棒性以防止将一致性模型弱化到此范围内的问题。我们研究了这个问题的渐近复杂性,并提出了基于抽象建立鲁棒性的有效技术。有两种重要的情况需要考虑:分别对用 PC 替换 SI 和用 CC 替换 PC 的鲁棒性。可以将这两种情况的结合作为对用 CC 替换 SI 的鲁棒性。
在第一种情况下(SI vs PC),检查程序 $\P$ 的稳健性被简化为 $\P$ 在 PC 下与监视器组合的可达性(断言检查)问题,该监视器检查 PC 行为是否为“异常”,即在 PC 下被 $\P$ 承认,但在 SI 下不被承认。这种方法提出了两个非平凡的挑战:(1)定义一个监视器来检测 PC vs SI 异常,该监视器使用最少量的辅助内存(记住过去的事件),以及(2)确定检查 $\P$ 与监视器的组合是否在(较弱的)模型 PC 下到达特定控制位置 1 的复杂性。有趣的是,我们通过研究这两个弱一致性模型 PC 和 SI 与可序列化之间的关系来解决这两个挑战。监视器的构建基于这样一个事实:PC vs SI 异常可以粗略地定义为 PC vs SER 异常与 SI vs SER 异常之间的差异(在先前的工作 [13] 中进行了研究),并且我们表明 PC 下的可达性问题可以简化为 SER 下的可达性问题。这些结果导致该鲁棒性问题(对于任意程序)在多项式时间内简化为 SER 下的可达性问题,这从实用的角度来看很重要,因为 SER 语义(而不是 PC 或 SI 语义)可以在现有的验证工具中轻松编码(使用锁来保护事务的隔离)。这些结果还能够精确地表征该问题的复杂性类别。
检查用 CC 代替 PC 的稳健性归结为检查用 CC 代替 SER 的稳健性的问题。在 [10] 中,后者已被证明可以在多项式时间上归结为 SER 下的可达性。这个令人惊讶的结果依赖于上面提到的从 PC 可达性到 SER 可达性的归结。这种归结表明,给定程序 $\P$ 在 PC 下到达某个控制位置当且仅当转换后的程序 $\P$ (其中本质上每个事务被分成两部分,一部分包含所有读取,另一部分包含所有写入)在 SER 下到达相同的控制位置。由于这种归结保留了程序的结构,程序 $\P$ 的 CC vs PC 异常对应于转换后的程序 $\P$ 的 CC vs SER 异常。
除了实现这些归约之外,对异常类别的表征或从 PC 语义到 SER 语义的归约对于更好地理解这些弱一致性模型及其之间的差异也很重要。我们相信这些结果可以找到超越稳健性检查的应用,例如验证是否符合给定的规范。
作为一种更务实的建立稳健性的方法,避免了 SER 下的不可达性证明,我们引入了一种证明方法,该方法基于 Lipton 的归约理论 [39] 和 [9] 中引入的交换依赖图概念,它表示程序中事务之间的移动者类型依赖关系。我们给出了上述所有情况下的稳健性的充分条件(从正文可知应该是充要条件),这些条件表征了与给定程序相关的交换依赖图。
我们在包含从以前的工作中提取的七个具有挑战性的应用程序的基准上测试了这些验证技术的适用性 [30, 34, 19]。对于所有一致性模型的组合,这些技术足够精确,可以证明或反驳所有这些应用程序的稳健性。
完整证明和更多细节可以在[11]中找到。
Overview
我们概述了本文研究的稳健性问题,首先讨论 PC 与 CC 的情况,然后讨论 SI 与 PC 的情况。最后我们用一个例子来说明基于交换性论证的稳健性检查技术。
Robustness PC vs CC
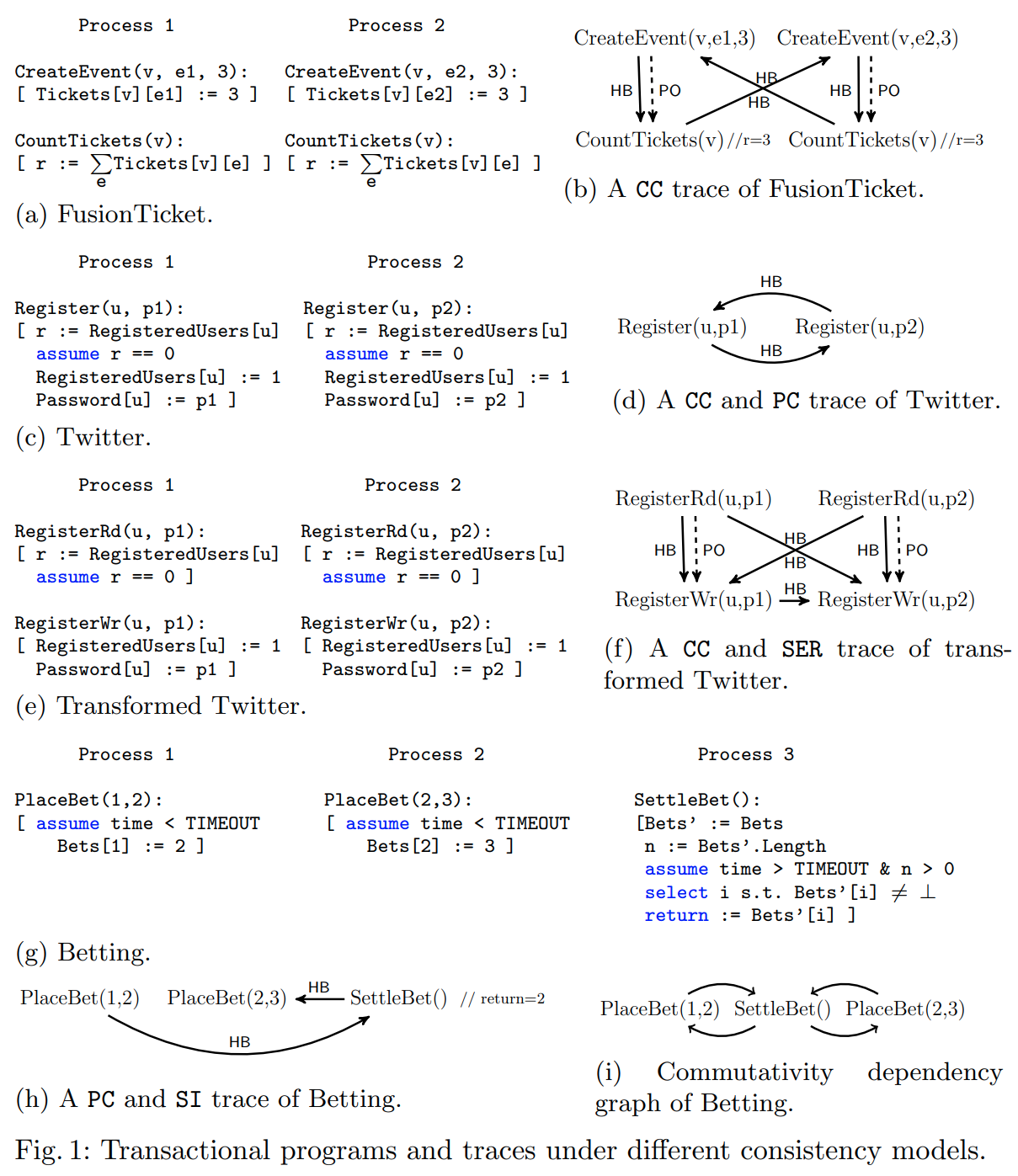
我们使用 FusionTicket 和 Twitter 程序来说明将 PC 替换为 CC 时的健壮性,分别如图 1a 和图 1c 所示。FusionTicket 管理多个事件的票务,每个事件与一个场馆相关联。它的状态由一个二维映射组成,存储某个场馆中的事件的票数($r$ 是局部变量,$\CountTickets$ 中的赋值被解释为对共享状态的读取操作)。该程序包含两个进程,每个进程包含两个事务。第一个事务在场馆 $v$ 中创建一个事件 $e$,并分配若干张票,第二个事务计算该场馆中所有事件的票总数。该程序的一个可能的规范是 $\CountTickets$ 中计算的值是单调递增的,因为每个值都是在创建新事件之后计算的。
Twitter 提供了一个用于注册新用户的事务,该事务由两个并行进程执行。其状态包含两个映射,分别记录给定用户名是否已注册($0$ 表示未注册,$1$ 表示已注册)以及该用户名的密码。每个事务首先检查用户名是否可用(见 $\assume$ 语句)。期望的规范是,当注册事务成功时,用户必须使用指定的密码进行注册。
如果某个程序在两个模型下的行为集合相同,那么它就是健壮的。我们将程序的行为建模为轨迹,轨迹记录了事务之间的标准控制流和数据流依赖关系,例如同一会话中事务之间的顺序,以及一个事务是否读取了另一个事务写入的值(read-from 关系)。这些依赖关系的并集的传递闭包称为 happens-before。图 1b 显示了 FusionTicket 的一个轨迹,其中每个事务读取的具体值在注释中给出。在该轨迹中,每个进程分别在同一场馆中注册了不同的事件,且每个进程在计算该场馆的票数时忽略了另一个进程创建的事件。
图 1b 显示了 FusionTicket 在 CC 下的一个轨迹,它表明 FusionTicket 并不健壮,因为该轨迹在 PC 下是不允许的。此轨迹违反了期望的规范,因为票数并未增加(两个进程中的票总数均为 $3$)。happens-before 依赖关系(标记为 $\HB$ 的边)包括程序顺序 $\PO$(同一进程中的事务顺序)和读写依赖关系,因为 $\CountTickets(v)$ 没有观察到另一个进程中的 $\CreateEvent$ 事务写入的值(后者覆盖了前者读取的一些值)。该轨迹在 CC 下是允许的,因为事务 $\CreateEvent(v, e1, 3)$ 与另一个进程中的 $\CountTickets(v)$ 事务并发执行,$\CreateEvent(v, e2, 3)$ 事务的情况类似。然而,在 PC 下是不允许的,因为无法定义一个总的提交顺序来解释两个 $\CountTickets(v)$ 事务的读取结果(这些读取应对应于该顺序的某个前缀的更新)。例如,假设 $\CreateEvent(v, e1, 3)$ 在 $\CreateEvent(v, e2, 3)$ 之前提交,那么第二个进程中的 $\CountTickets(v)$ 必须观察到 $\CreateEvent(v, e1, 3)$ 的效果,因为它已经观察到了 $\CreateEvent(v, e2, 3)$ 的效果。然而,这与 $\CountTickets(v)$ 计算票数为 $3$ 的结果相矛盾。
另一方面,Twitter 在将 PC 替换为 CC 时是健壮的。例如,图 1d 显示了 Twitter 在 CC 下的一个轨迹,其中两个事务 $\Register(u,p1)$ 和 $\Register(u,p2)$ 并发执行,并且它们的写入操作互不知晓(它们之间没有因果关系)。$HB$ 依赖关系包括写写依赖关系,因为两个事务都对同一个位置执行写操作(我们认为进程 2 中的事务是最后一个写入 $\Password$ 映射的事务),并且存在读写依赖关系,因为每个事务都读取了由另一个事务写入的 $RegisteredUsers$。该轨迹在 PC 下也是允许的,因为可以定义提交顺序,使得 $\Register(u,p1)$ 在 $\Register(u,p2)$ 之前提交,然后两个事务都从初始状态(空前缀)读取数据。注意,该轨迹存在循环的 happens-before 关系,这意味着它在串行化模型下是不允许的。
Checking robustness PC vs CC
Robustness SI vs PC
Checking robustness SI vs PC
Checking robustness using commutativity arguments
Consistency Models
Robustness
Robustness Against CC Relative to PC
我们证明,相对于 PC 验证针对 CC 的稳健性可以被归约为相对于 SER 验证针对 CC 的稳健性。归约的关键在于构建一个程序转换,使得在 SER 下模拟程序 $\P$ 的 PC 语义,并且进一步将相对于 CC 与 SER 的稳健性验证在多项式时间内归约到 SER 下的可达性问题 [10]。
给定一个包含事务集合 $\Tr(\P)$ 的程序 $\P$,我们定义一个程序 $\P_\clubsuit$,其中 $\P$ 中的每个事务 $t \in \Tr(\P)$ 被分解为两个事务:$t[r]$ 包含 $t$ 中的所有读和 $\assume$ 语句(保持顺序不变),而 $t[w]$ 则包含 $t$ 中的所有写语句(保持顺序不变)。在接下来的部分中,我们证明如下定理:
定理 1 CC 下对 PC 鲁棒性充要条件
程序 $\P$ 在 CC 下相对于 PC 鲁棒,当且仅当 $\P_\clubsuit$ 在 CC 相对于 SER 鲁棒。
直观上,在 PC 下,进程可以并发地执行多个事务,这些事务可以从中央内存中抓取相同的一致快照,并随后提交其写操作。将一个事务的读部分与写部分解耦允许在 SER 下模拟这种行为。
本定理的证明依赖于几个关于 $\P$ 和 $\P_\clubsuit$ 的轨迹之间关系的中间结果。设 $\tau = (\rho, \PO, \WR, \WW, \RW) \in \Tr_X(\P)$ 是程序 $\P$ 在语义 $X$ 下的轨迹。我们定义轨迹 $\tau_\clubsuit = (\rho_\clubsuit, \PO_\clubsuit, \WR_\clubsuit, \WW_\clubsuit, \RW_\clubsuit)$,其中 $\tau$ 中的每个事务 $t$ 被分解为两个事务 $t[r] \in \tau_\clubsuit$ 和 $t[w] \in \tau_\clubsuit$,而依赖关系也进行了相应的调整,即:
- $\PO_\clubsuit$ 是最小的传递关系,包含每个 $t$ 的 $(t[r], t[w])$,以及若 $(t, t') \in \PO$,则包含 $(t[w], t'[r])$;
- 若 $(t'[w], t[r]) \in \WR_\clubsuit$,则 $(t', t) \in \WR$;若 $(t'[w], t[w]) \in \WW_\clubsuit$,则 $(t', t) \in \WW$;若 $(t'[r], t[w]) \in \RW_\clubsuit$,则 $(t', t) \in \RW$。
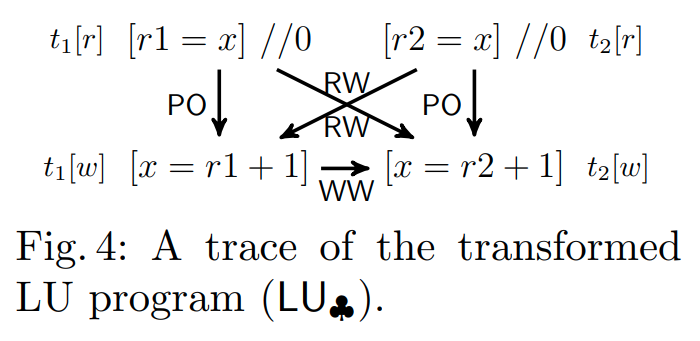
例如,图 4 展示了 LU 轨迹 $\tau$ 在图 3(b) 中给出的轨迹的 $\tau_\clubsuit$。对于包含单一事务的轨迹,例如图 3(a) 中的 SB,$\tau_\clubsuit$ 与 $\tau$ 一致。
反之,对于程序 $\P_\clubsuit$ 在语义 $X$ 下的轨迹 $\tau_\clubsuit = (\rho_\clubsuit, \PO_\clubsuit, \WR_\clubsuit, \WW_\clubsuit, \RW_\clubsuit) \in \Tr_X(P_\clubsuit)$,我们定义轨迹 $\tau = (\rho, \PO, \WR, \WW, \RW)$,其中每对组件 $t[r]$ 和 $t[w]$ 被合并为一个事务 $t \in \tau$。依赖关系也按相应方式定义,例如若 $(t'[w], t[w]) \in \WW_\clubsuit$,则 $(t', t) \in \WW$。
以下引理表明,对于任意语义 $X \in \set{\CC, \PC, \SI}$,如果 $\tau \in \Tr_X(P)$,那么 $\tau_\clubsuit$ 是程序 $\P_\clubsuit$ 在 $X$ 下的一个有效轨迹,即 $\tau_\clubsuit \in \Tr_X(P_\clubsuit)$。直观上,该引理表明,分解轨迹并适当地定义依赖关系不会在这些关系中引入环,并且保持了不同一致性公理的有效性。
此引理的证明依赖于从轨迹 $\tau$ 中的因果关系 $\CO$ 和仲裁顺序 $\ARB$ 构造轨迹 $\tau_\clubsuit$ 的因果关系 $\CO_\clubsuit$ 和仲裁顺序 $\ARB_\clubsuit$。在 CC 情况下,这些是最小的传递关系,使得:
- $\PO_\clubsuit \subseteq \CO_\clubsuit \subseteq \ARB_\clubsuit$,且
- 如果 $(t_1, t_2) \in \CO$,那么 $(t_1[w], t_2[r]) \in \CO_\clubsuit$;如果 $(t_1, t_2) \in \ARB$,那么 $(t_1[w], t_2[r]) \in \ARB_\clubsuit$。
对于 PC 和 SI,需要满足的额外条件是:如果 $(t_1, t_2) \in \ARB$,那么 $(t_1[w], t_2[w]) \in \CO_\clubsuit$。这是为了满足公理 $\AxPrefix$,即 $\ARB_\clubsuit; \CO_\clubsuit \subset \CO_\clubsuit$,当 $(t_1[w], t_2[r]) \in \ARB_\clubsuit$ 且 $(t_2[r], t_2[w]) \in \CO_\clubsuit$ 时。
这种构造确保了 $\CO_\clubsuit$ 是一个偏序关系,并且 $\ARB_\clubsuit$ 是一个全序关系,因为 $\CO$ 是偏序关系,$\ARB$ 是全序关系。此外,基于上述规则,我们有:如果 $(t_1[w], t_2[r]) \in \CO_\clubsuit$,那么 $(t_1, t_2) \in \CO$;同样,如果 $(t_1[w], t_2[r]) \in \ARB_\clubsuit$,那么 $(t_1, t_2) \in \ARB$。
引理 1
如果 $\tau \in \Tr_X(P)$,则 $\tau_\clubsuit \in \Tr_X(P_\clubsuit)$。
在 $X$ 为 CC 的情况下,我们给出 CC 轨迹的重要特征。该特征以非循环性质陈述。
引理 2
轨迹 $\tau$ 是 CC 轨迹,当且仅当 $\ARB^+_0$ 和 $\CO^+_0; \RW$ 是无环的($\ARB_0$ 和 $\CO_0$ 在表 1 中定义)。
接下来我们证明,程序 $\P$ 的轨迹 $\tau$ 是 CC,当且仅当相应的轨迹 $\tau_\clubsuit$ 是 CC。该结果基于以下观察:在 $\ARB^+_0$ 或 $\CO^+_0; \RW$ 中的环不能通过分解事务来打破。
引理 3
程序 $\P$ 的轨迹 $\tau$ 是 CC,当且仅当相应的轨迹 $\tau_\clubsuit$ 是 CC。
以下引理表明,轨迹 $\tau$ 是 PC,当且仅当相应的轨迹 $\tau_\clubsuit$ 是 SER。证明的 “if” 方向基于从轨迹 $\tau_\clubsuit$ 中的仲裁顺序 $\ARB_\clubsuit$ 构造轨迹 $\tau$ 的因果关系 $\CO$ 和仲裁顺序 $\ARB$(因为 $\tau_\clubsuit$ 是可序列化轨迹,$\CO_\clubsuit$ 和 $\ARB_\clubsuit$ 一致)。这些关系是最小的传递关系,使得:
- 如果 $(t_1[w], t_2[r]) \in \ARB_\clubsuit$,那么 $(t_1, t_2) \in \CO$;
- 如果 $(t_1[w], t_2[w]) \in \ARB_\clubsuit$,那么 $(t_1, t_2) \in \ARB$。
“only-if” 方向基于以下事实:轨迹 $\tau$ 中在 PC 下被允许的依赖关系环(在引理 7 中表征),在分解事务后被打破。此外,分解事务不会引入新的不源于 $\tau$ 的环。
引理 4
轨迹 $\tau$ 是 PC,当且仅当 $\tau_\clubsuit$ 是 SER。
Robustness Against PC Relative to SI
在本节中,我们展示了如何将针对 PC 相对于 SI 的健壮性检查在多项式时间内简化为 SER 语义下的可达性问题。我们复用了前一节中的程序转换,该转换允许在 SER 上模拟 PC 行为,并且我们进一步提供了区分 PC 语义和 SI 语义的轨迹特征。我们使用这一特征来定义一种能够检测程序是否存在此类轨迹的仪器(监控器)。
我们证明了,健壮性违反中(针对 PC 相对于 SI 的健壮性)的 happens-before 循环必须包含 WW 依赖关系,接着是 RW 依赖关系,并且它们不应包含两个连续的 RW 依赖关系。这是因为,每个 PC 轨迹中的 happens-before 循环必须包含两个连续的 RW 依赖关系,或者包含 WW 依赖关系和 RW 依赖关系。否则,happens-before 循环将暗示仲裁顺序中的循环。因此,PC 下的任何轨迹中,如果它的所有简单的 happens-before 循环都包含两个连续的 RW 依赖关系,那么在 SI 下也是可能的。例如,图 3b 中的非健壮 LU 执行轨迹包含 WW 依赖关系和 RW 依赖关系,但不包含两个连续的 RW 依赖关系,这是 SI 不允许的。而图 3c 中的健壮 WS 执行轨迹则包含两个连续的 RW 依赖关系。作为第一步,我们证明了以下定理,它描述了 PC 和 SI 都允许的轨迹特征。
定理 2 PC 下相对 SI 鲁棒性充要条件
程序 $\P$ 相对于 SI 对 PC 具有鲁棒性,当且仅当 PC 下的 $\P$ 踪迹中的每个 happens-before 环包含两个连续的 RW 依赖关系。
在证明上述定理之前,我们首先给出一些中间结果,这些结果描述了 PC 或 SI 轨迹中的循环特征。首先,我们展示了任何简单的 happens-before 循环包含两个连续的 RW 的 PC 轨迹也是 SI 轨迹。
引理 5
如果轨迹 $\tau$ 是 PC 且所有 happens-before 循环都包含两个连续的 RW 依赖关系,则 $\tau$ 是 SI。
定理 2 的证明还依赖于以下引理,该引理描述了 SI 允许的 happens-before 循环。
引理 6 [23, 13]
如果轨迹 $\tau$ 是 SI,则它的所有 happens-before 循环都必须包含两个连续的 RW 依赖关系。
定理 2 的证明:对于必要条件,如果程序 $\P$ 以针对 PC 相对于 SI 是健壮的,则 $\P$ 在 PC 下的每一个轨迹 $\tau$ 也是 SI 轨迹。因此,依据引理 6,$\tau$ 中的所有循环都包含两个连续的 RW 依赖关系,这证明了该方向的必要性。反之,假设 $\tau$ 是 $\P$ 的一个 PC 轨迹,并且所有 happens-before 循环都包含两个连续的 RW 依赖关系。那么依据引理 5,$\tau$ 是 SI。因此,P 在 PC 下的每个轨迹 $\tau$ 都是 SI 的。故此证毕。
接下来,我们给出了一个重要的引理,它描述了 PC 语义下可能的 happens-before 循环。这是 [13] 中结果的增强版本,后者表明 PC 下的所有 happens-before 循环必须包含 {RW, WW} 中的两个连续依赖关系,并且至少包含一个 RW 依赖关系。我们展示了这两个连续依赖关系不能是 RW 之后是 WW,或者两个连续的 WW。
引理 7:如果轨迹 $\tau$ 是 PC,则 $\tau$ 中的所有 happens-before 循环都必须包含两个连续的 RW 依赖关系,或者包含 WW 依赖关系接着是 RW 依赖关系。
结合定理 2 和引理 4、引理 7 的结果,我们得到了如下定理,它描述了违反针对 PC 相对于 SI 的健壮性的轨迹特征。
定理 3
程序 $\P$ 对 PC 相对于 SI 不具有鲁棒性当且仅当在 SER 下存在 P♣ 的迹 τ♣,使得通过合并 τ♣ 中的 8 个读写事务所获得的迹 τ 包含一个发生于之前的循环,该循环不包含两个连续的 RW 依赖关系,并且它包含一个 WW 依赖关系,后跟一个 RW 依赖关系。
定理 4
当且仅当图 6 中的插桩在 SER 下执行时不违反断言,程序 $\P$ 相对于 SI 对 PC 具有鲁棒性
定理 5 CC 下相对 SI 鲁棒性的充要条件
程序 $\P$ 相对于 SI 对 CC 具有鲁棒性当且仅当 $\P$ 相对于 PC 对 CC 具有鲁棒性,且 $\P$ 相对于 SI 对 PC 具有鲁棒性。
Proving Robustness Using Commutativity Dependency Graphs
Experimental Evaluation
Related Work
本文中的一致性模型在最近的几篇论文中进行了研究[21、20、25、43、16、44、14]。其中大部分都集中在它们的操作和公理形式化上。我们在本文中使用的形式化定义基于[25、16]中给出的定义。Biswas 和 Enea [14] 表明,检查执行是否为 CC 是多项式时间,而检查执行是否为 PC 或 SI 是 NP 完全的。
本文研究的稳健性问题已在弱内存模型的背景下进行了研究,但仅相对于顺序一致性,针对 Release/Aquire (RA)、TSO 和 Power [36, 17, 15, 29]。在 [9, 10] 中已经研究了相对于 SER 的 CC 和 SI 的稳健性检查。在这项工作中,我们研究了两个弱一致性模型之间的稳健性问题,这带来了不同的非平凡挑战。特别是,以前的工作提出了在顺序一致性 (或 SER) 下降低可达性,这依赖于最小稳健性违规概念 (w.r.t. 操作语义),这不适用于我们的情况。PC 和 SER 之间的关系在精神上类似于 Biswas 和 Enea [14] 在检查执行是否为 PC 的背景下给出的关系。然而,这种关系是在“较弱”的跟踪概念(仅包含程序顺序和读取)的背景下证明的,并且它不扩展到我们的跟踪概念。例如,该结果并不意味着保留在我们的案例中至关重要的 WW 依赖性。
一些研究描述了各种过度或欠近似分析,用于检查相对于 SER 的稳健性。[13、18、19、26、40] 中的研究提出了基于计算一组计算的抽象的静态分析技术,用于证明稳健性。具体来说,[19、40] 使用 FOL 公式对弱一致性模型下的程序执行进行编码,以描述执行中动作之间的依赖关系。这些方法可能会由于其编码中考虑的抽象而返回错误警报。请注意,在本文中,我们证明了 [13] 的结果在 PC 允许的发生前循环形状方面的加强。
基于轨迹的鲁棒性的另一种选择是基于状态的鲁棒性,它要求如果两个语义下的可达状态集一致,则程序是鲁棒的。虽然状态鲁棒性是保留状态不变量的必要和充分概念,但它的验证(即在弱语义模型下计算可达状态集)通常是一个难题。已经在 TSO 和 Power 等宽松记忆模型的背景下研究了该问题的可判定性和复杂性,并且已经证明它要么是可判定的但非常复杂(非原始递归),要么是不可判定的 [5, 6]。已经提出了使用抽象或有界分析来自动检查近似可达性/不变量的程序,例如 [7, 4, 28, 1]。还开发了用于在弱一致模型背景下验证不变量的证明方法,例如 [37, 32, 41, 3]。但是,这些方法不提供决策程序。

