\[ \def\K{\mathsf{K}} \def\V{\mathsf{V}} \def\H{\mathcal{H}} \def\R{\mathsf{R}} \def\W{\mathsf{W}} \def\read{\mathsf{read}} \def\WT{\mathsf{WT}} \def\RT{\mathsf{RT}} \def\po{\mathsf{\textcolor{red}{po}}} \def\wr{\mathsf{\textcolor{teal}{wr}}} \def\SO{\mathsf{\textcolor{purple}{SO}}} \def\WR{\mathsf{\textcolor{teal}{WR}}} \def\CM{\mathsf{\textcolor{orange}{CM}}} \def\CO{\mathsf{\textcolor{brown}{CO}}} \def\CMto{\xrightarrow{\CM}} \def\COto{\xrightarrow{\CO}} \def\WRto{\xrightarrow{\WR}} \def\WRxto{\xrightarrow{\WR(x)}} \def\wrxto{\xrightarrow{\wr(x)}} \def\potto{\xrightarrow{\po_t}} \]
摘要
现代数据库采用弱隔离级别来满足高可用性事务。然而，最近许多生产数据库中都出现了弱隔离错误。这引发了人们对数据库实现是否在实践中真正实现其承诺的隔离保证的担忧。在本文中，我们介绍了 Plume，这是第一个高效、完整的弱隔离级别黑盒检查器。Plume 建立在模块化、细粒度、事务异常模式的基础上，我们利用这些模式建立了代表性弱隔离级别的合理和完整特征，包括读取提交、读取原子性和事务因果一致性。Plume 利用两种技术（向量和树时钟）的新颖组合来加速隔离检查。我们广泛的评估表明，Plume 可以在大量异常数据库执行历史中重现所有已知违规行为，在三个生产数据库中检测新的隔离错误以及信息反例，比最先进的检查器发现更多的弱隔离异常，并在各种工作负载下有效地验证隔离保证。
作者：
- SI LIU, ETH Zurich, Switzerland
- LONG GU, State Key Laboratory for Novel Software Technology, Nanjing University, China
- HENGFENG WEI*, State Key Laboratory for Novel Software Technology, Nanjing University, China
- DAVID BASIN, ETH Zurich, Switzerland
Introduction
现代 ACID 和 NewSQL 数据库通常采用弱隔离级别，以适应高可用性事务（HAT）。这些弱隔离级别也称为 HAT 隔离级别（或保证）[Bailis et al 2013a,b]。即使在存在网络分区的情况下，HAT 也能确保系统“始终在线”运行，从而避免了更强的隔离级别（如快照隔离和可序列化）的性能损失。尽管如此，它们仍然为数据库用户和应用程序程序员提供了有用的语义，例如原子可见性和因果一致性。过去十年，人们在设计高可用性、弱隔离的分布式事务方面进行了持续、深入的努力 [Akkoorath et al 2016; Bailis et al 2016; Cheng et al 2021; Didona et al 2018; Liu 2022; Liu et al 2024b; Lloyd et al 2013; Lu et al 2020]。近年来，HAT 语义在数据库之外也有了众多应用，包括无服务器计算 [Lykhenko et al 2021; Wu et al 2020] 和微服务 [Ferreira Loff et al 2023; Pereira and Silva 2023]。
符合 HAT 的弱隔离保证包括 SQL-92 标准化读取已提交 [Berenson et al 1995]，这是大多数 SQL 数据库的默认级别 [Bailis et al 2013a; Crooks et al 2017]，以及读取原子性（RA）[Bailis et al 2016]，它已在现实世界中得到广泛应用，例如二级索引和外键约束，最近已在 Facebook 的 TAO 上分层以提供原子可见事务 [Cheng et al 2021]。值得注意的是，事务因果一致性（TCC）[Akkoorath et al 2016; Lloyd et al 2013] 代表了分布式计算和数据库社区的成功结合，它通过扩展因果一致性 [Ahamad et al 1995; Perrin et al 2016]（始终可用系统中可实现的最强一致性级别 [Attiya et al 2015]）和事务保证。过去十年，在高可用性和高性能 TCC 数据库系统方面取得了大量学术进展 [Akkoorath et al 2016; Didona et al 2018; Du et al 2014; Liu et al 2024b; Lloyd et al 2013; Lu et al 2020; Mehdi et al 2017]。TCC 及其变体的近期生产采用包括 Neo4j [2023]（通过“书签”事务）、ElectricSQL [2023]（成功从 Cure [Akkoorath et al 2016] 过渡到生产）和 Azure Cosmos DB [Microsoft 2023]（为其事务批处理提供会话保证和前缀一致性 [Burckhardt et al 2015]）。
然而，许多声称提供 HAT 或更强隔离级别的生产数据库中都出现了 HAT 隔离错误 [Biswas and Enea 2019; Huang et al 2023; Jepsen 2024b]（违反弱隔离保证（例如 TCC）也会违反更强的隔离保证（例如可序列化性）。提供更强隔离保证的数据库本质上不会出现弱隔离错误）。这引发了人们对数据库实现是否真正在实践中兑现其承诺的服务级别协议的担忧。许多黑盒测试和验证工作 [Biswas and Enea 2019; Huang et al 2023; Kingsbury and Alvaro 2020; Tan et al 2020; Zhang et al 2023]（由于数据库内部通常不可用或难以理解）一直致力于发现隔离异常并验证隔离是否完成。两个代表性的黑盒检查器是最近的 dbcop [Biswas and Enea 2019] 和 Elle [Kingsbury and Alvaro 2020]，它们都成功检测到了现实世界的 HAT 隔离错误并表现出良好的性能。
Research Gaps
尽管最近取得了这些进展，但现有研究仍未完全解决一些挑战。
- G1（完整性）：大多数检查器都会漏掉错误。其中一些 [Tan et al 2020; Zhang et al 2023] 专注于事务间依赖关系，而事务内部出现的隔离错误也很关键 [Huang et al 2023]，例如在 MySQL [Kingsbury 2023] 和 MariaDB ($$5.2）中检测到的不可重复读取。此外，对于较新的隔离级别（例如 RA 和 TCC），Elle 会搜索来自不同形式主义的混合异常 [Adya 1999; Cerone et al 2015]，这些异常尚不清楚是否能完全表征所讨论的隔离级别。
- G2（效率）：尽管弱隔离级别是多项式时间可检查的 [Biswas and Enea 2019]（相对于收集的数据库执行历史记录），但现有工具中的图遍历 [Biswas and Enea 2019; Kingsbury 和 Alvaro 2020] 在实践中通常需要大量时间，在高并发工作负载（例如偏斜的键访问或大量客户端）下搜索循环（表示异常）。然而，这样的工作负载对于压力测试或验证数据库是可取的。尽管使用高级求解器 [Bayless et al 2015; Potassco 2023] 来检查隔离级别的趋势日益增加，但编码和解决依赖约束在实践中仍然很昂贵。
- G3（可理解性）：基于求解器的工具通常会返回难以解释的反例，如不满足的子句。利用图遍历的工具可能会报告较大的循环，这对于故障机制也是无用的。此外，根据隔离级别底层特征的粒度，现有工具可能无法直接区分不同的异常，例如断裂读取和非单调读取，而这些异常与不同的并发控制机制相关 [Bailis et al 2013a, 2016]。所有这些都使得理解和调试违规变得困难。
The Plume Checker
我们提出了一种名为 Plume 的新型黑盒检查器，用于检查弱 HAT 隔离保证。Plume 基于两个概念转变来填补上述所有空白。
受 HAT 隔离级别的语义构建块的启发，例如不可重复读取 [Bailis et al 2013a]、原子可见性 [Bailis et al 2016]、因果一致性 [Perrin et al 2016] 和数据收敛 [Akkoorath et al 2016; Lloyd et al 2011]，我们设计了 14 个模块化、细粒度、事务异常模式（transactional anomalous patterns, TAP）来表征 HAT 隔离级别。我们以 Biswas 和 Enea [2019] 的公理框架为基础进行表征，用于定义隔离级别。尽管如此，我们采取了概念上不同的视角，通过它们的异常来定义它们，为此我们建立了健全性（无误报）和完整性（不遗漏任何异常）。
这种概念上的转变使我们能够有效地解决 G1 和 G3，如下所示。首先，我们基于 TAP 的表征使 Plume 能够检测事务执行历史中所有可能的 HAT 隔离违规，就像在数据库隔离保证的黑盒测试中一样（G1）。这是非常可取的，特别是考虑到特定隔离错误的发生通常是不可预测的，而现有的黑盒检查器通常采用随机测试生成。此外，由于我们的 TAP 是细粒度的，因此它还对应于数据库系统底层构建块的特定缺陷，例如事务的原子承诺或维持因果关系的缺陷。这使 Plume 能够报告违规场景的信息性反例，帮助开发人员发现其原因（G3）。
除了单个异常（包括一个用于切割隔离的 TAP [Bailis et al 2013a]）之外，我们的模块化 TAP 还可以可靠且完整地检查其他 HAT 隔离级别。在 Plume 中启用 9 个 TAP 可检查读取已提交。使用另外 3 个 TAP，Plume 可检查读取原子性。所有 14 个 TAP 都相当于检查事务因果一致性。
为了克服 G2，我们首先利用我们的见解，即 SMT 求解器专门用于解决不确定的依赖关系（例如并发写入的顺序），然而，这些依赖关系主要存在于更强的隔离级别（例如快照隔离和可序列化性）中 [Huang et al 2023; Tan et al 2020; Zhang et al 2023]。因此，我们在检查弱 HAT 隔离保证时采用非基于求解器的图遍历，以减轻编码和解决不确定依赖关系的高开销。
此外，受数十年来使用向量 [Fidge 1988] 设计因果一致性数据库的实践启发，我们利用向量来黑盒检查隔离级别，包括迄今为止可实现的最强 HAT 隔离级别，即 TCC。这种概念转变使 Plume 能够通过使用向量捕获和存储事务之间的传递因果依赖关系来加速图遍历以进行可达性检查和循环检测。更具体地说，Plume 在构建事务依赖图期间保持以下不变量：当且仅当 \(t_2\) 的关联向量大于或等于 \(t_1\) 的关联向量时，事务 \(t_2\) 才可从事务 \(t_1\) 到达。然后，循环检测相当于检查是否有两个事务具有相同的向量。此外，由于这个不变量，在错误搜索或向量更新期间，遍历可以在遇到具有较大向量的事务时尽早回溯。这是因为下游事务的向量至少与当前事务一样大。
为了进一步加快 Plume 的速度，我们还在向量的使用中采用了树时钟 [Mathur et al 2022] 数据结构，这是并发程序分析的最新进展。这大大减少了比较和连接向量所需的时间，而这些时间是由于大量客户端会话和事务依赖关系而产生的。
Contributions
总体而言，本文做出了以下贡献。
- 我们引入了一组模块化、细粒度的 TAP，用于捕获各种隔离异常。使用这些 TAP，我们正式建立了四种普遍的 HAT 隔离级别的合理和完整特征（\(\S 3\)）；
- 我们设计了一种高效的基于 TAP 的检查算法，利用向量和树时钟的组合来加速隔离异常的搜索（\(\S 4\)）；
- 我们在 Plume 中实现了我们的算法，Plume 是一种用于检查不同隔离级别和单个异常的工具。我们还在各种基准上对 Plume 以及最先进的黑盒隔离检查器进行了广泛的评估（\(\S 5\)）。
我们的实验表明，Plume 可以
- 在最近的测试活动存档的 3000 多个异常历史记录中重现所有已知的隔离错误，
- 使用信息反例检测三种不同类型的生产数据库引擎中的新隔离错误，
- 比最先进的检查器发现更多的 HAT 隔离异常，
- 在各种基准测试中大大优于 bechmarks，
- 扩展到大工作负载，在五分钟内成功检查了 1,000,000 个事务和超过 50,000,000 个操作。
这项工作还补充了两条研究路线：
- 在理论层面，先前的努力 [Adya 1999; Berenson et al 1995; Bouajjani et al 2017] 关于使用异常来忠实地表征数据一致性属性，然而，这些属性并不涵盖较新的 HAT 语义，例如读取原子性和事务因果一致性；
- 在实践层面，检查更强的隔离级别方面取得了最新进展，包括用于快照隔离的 PolySI [Huang et al 2023] 和 Viper [Zhang et al 2023] 以及用于可序列化的 Cobra [Tan et al 2020]。
Background
Weak HAT Isolation Levels
数据库提供各种隔离级别（或保证），如图 1 所示，以适应数据一致性和性能之间的不同权衡。虽然高可用性事务（HAT）提供了并发性和性能优势，但它们无法实现所有可能的隔离保证 [Bailis et al 2013a]。我们简要解释本研究重点关注的符合 HAT 的隔离级别的非正式定义，并将其正式定义推迟到 \(\S 3.1\)。
- 切割隔离（CI）。每个事务都应从数据项的非变化快照中读取 [Bailis et al 2013a]。它可以防止不可重复的读取 [Berenson et al 1995]。例如，如果事务多次读取同一个数据项，它应该始终看到相同的值。
- 已提交读（RC）。这是许多数据库的默认隔离级别，它保证事务只读取其他事务所做的已提交更改。它避免了脏读（读取从未提交的值）[Berenson et al 1995]，但允许非重复读等异常。
- 读取原子性（RA）。这可确保事务的所有更新或所有更新均不被其他事务观察到。它禁止断裂读取异常 [Bailis et al 2016]，例如 Rachel 只观察社交网络中 Joe 和 Ross 之间新（双向）友谊的一个方向。
- 事务因果一致性（TCC）。直观地说，这种隔离保证结合了非事务因果一致性（CC）和事务 RA，并通过额外的数据收敛保证得到增强 [Akkoorath et al 2016; Lloyd et al 2013]。
CC 要求两个有因果关系的（非事务性）读取或写入操作必须以相同的因果顺序出现在所有客户端会话（客户端会话通常指客户端和服务器之间的交互时间，例如登录和退出数据库应用程序之间）中 [Ahamad et al 1995; Perrin et al 2016]。它可以防止因果关系违规，例如 Rachel 观察到 Joe 对 Ross 消息的回复，但没有看到消息本身。但是，因果关系不相关的事务可能会在不同会话中以不同的顺序出现，这可能会导致在并发冲突更新的情况下这些会话的视图永久分歧。例如，Joe 和 Ross 在公路旅行计划器中独立将会面地点更新为“我的地方”可能会造成混淆。收敛属性通过要求所有视图最终收敛到相同状态 [Akkoorath et al 2016; Lloyd et al 2011]（例如，通过应用 LWW（最后写入者获胜）规则 [Burckhardt et al 2014]）来防止这种情况。因此，Rachel 和 Monica 的最终排名相同。
Black-box Database Isolation Checking
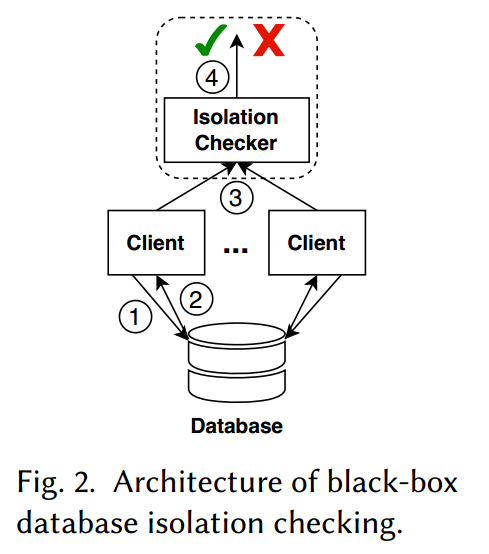
数据库隔离保证的黑盒检查通常按如下方式进行，如图 2 所示。客户端向可能被分区或复制的数据库发起事务请求（通常由某些随机工作负载生成器生成，例如，参见 \(\S 5.1\)）；尽管如此，数据库始终被视为黑盒（①）。每个客户端会话都会记录它发送的请求，例如对键 𝑥 的读取，以及数据库提供的相应结果，例如 𝑥 的值（②）。然后，来自每个客户端的所有日志被组合成统一的历史记录，随后提供给隔离检查器（③）。最后，检查器解决隔离检查问题：确定事务历史记录是否满足所讨论的隔离级别。在检测到错误后，一些检查器还会返回反例（④）。
前三个步骤是现有黑盒检查器采用的事实程序。但是，它们在最后一步的方法上有所不同，主要分为两类。在类别 (i) 中，隔离检查器（例如 Elle [Kingsbury and Alvaro 2020]）构建一种事务依赖图（例如 Adya 的有向序列化图 [Adya 1999]），并搜索表示隔离异常的循环。在类别 (ii) 中，像 PolySI [Huang et al 2023] 这样的检查器将依赖图和循环编码为逻辑公式（例如 SAT 公式），并调用现成的求解器（例如 MonoSAT [Bayless et al 2015]）。我们的方法属于类别 (i)，但利用事务异常模式来表示 HAT 隔离违规，并使用向量和树时钟的组合来加速违规搜索。
请注意，违反较弱的隔离保证（例如 TCC）也会违反较强的隔离保证（例如快照隔离）。正如我们将看到的（\(\S 5.2\)），在声称支持快照隔离甚至更强的可串行化的生产数据库中发现的许多隔离错误实际上是隔离级别（如切割隔离）更弱的错误。还要注意，满足更强隔离保证的历史自然会满足较弱的隔离保证。
假设。按照黑盒隔离检查的常见做法 [Biswas and Enea 2019; Huang et al 2023; Kingsbury and Alvaro 2020; Zhang et al 2023]，我们做出两个假设。首先，每个历史记录都包含一个特殊的事务，该事务写入所有键的初始值。此事务先于客户端会话中的所有其他事务。在实践中，我们通常在测试开始之前使用多个简短的只写事务来填充数据库。这些事务可以被视为单个逻辑上的只写事务。
其次，对于每个键，我们假设对该键的每次写入都会分配一个唯一值。因此，每次读取都可以与发出相应（指示）写入的事务唯一关联。然后可以在多项式时间内解决例如 TCC 的检查问题 [Biswas and Enea 2019]；否则，它通常是 NP-hard 的。在实际应用中，我们可以使用客户端标识符和本地计数器来保证写入值的唯一性。
Assumptions
按照黑盒隔离检查的常见做法 [Biswas and Enea 2019; Huang et al 2023; Kingsbury and Alvaro 2020; Zhang et al 2023]，我们做出两个假设。首先，每个历史记录都包含一个特殊的事务，该事务写入所有键的初始值。此事务先于客户端会话中的所有其他事务。在实践中，我们通常在测试开始之前使用多个简短的只写事务来填充数据库。这些事务可以被视为单个逻辑上的只写事务。
其次，对于每个键，我们假设对该键的每次写入都会分配一个唯一值。因此，每次读取都可以与发出相应（指示）写入的事务唯一关联。然后可以在多项式时间内解决例如 TCC 的检查问题 [Biswas and Enea 2019]；否则，它通常是 NP 难的。在实际应用中，我们可以使用客户端标识符和本地计数器来保证写入值的唯一性。
Characterizing HAT Isolation Levels via Anomalies
在本节中，我们将介绍我们的事务异常模式（TAP）。我们还使用这些 TAP 正式建立了四种流行的 HAT 隔离级别的合理和完整表征，即切割隔离（CI）、读取提交（RC）、读取原子性（RA）和事务因果一致性（TCC）。让我们首先描述正式基础。
Context and Definitions
我们考虑一个键值数据存储系统，它管理一组键 \(\K = \{ x, y, z, \dots \}\)，这些键与来自集合 \(\V\) 的值相关联。我们使用 \(R(x, v)\) 表示从 \(x \in \K\) 读取 \(v \in \V\) 的读取操作，使用 \(W(x, v)\) 表示向 \(x \in \K\) 写入 \(v \in \V\) 的写入操作。接下来，我们将对不相关的组件使用下划线来表示，并默认其存在。我们使用符号 \(\exists!\) 来表示“唯一存在性”。
二元关系 \(R\) 是 \(A\) 上的一个子集，即 \(R \subseteq A \times A\)。对于 \(a, b \in A\)，我们写作 \((a, b) \in R\) 或 \(a R b\)。定义 \(I_{A} \triangleq \{(a, a) \mid a \in A \}\) 为 \(A\) 上的同一关系，并定义 \(R^{-1} \triangleq \{(b, a) \mid (a, b) \in R \}\) 为 \(R\) 的逆关系。我们使用 \(R^{+}\) 表示 \(R\) 的传递闭包。若 \(R^{+} \cap I_{A} = \varnothing\)，则称关系 \(R\) 是无环的。严格偏序关系是不可自反且传递的关系。严格全序关系是严格偏序且全序的关系。
客户端通过发起事务与数据存储系统进行交互。
定义 1 事务 [Biswas and Enea 2019]
事务是一个二元组 \((O, \po)\)，其中 \(O\) 是操作集合，\(\po \subseteq O \times O\) 是操作上的严格全序关系，称为程序顺序。
我们用 \(t, t_1, t_2, \dots\) 来表示事务，并使用 \(O(t), O_x(t), R(t), R_x(t), W(t), W_x(t)\) 分别表示事务 \(t\) 中的操作集合、针对键 \(x\) 的操作集合、读取操作、读取 \(x\) 的操作、写入操作和写入 \(x\) 的操作。对于事务集合的扩展是直接的，例如，\(R(T) = \bigcup_{t \in T} R(t)\) 表示事务集合 \(T\) 中的所有读取操作。对于事务 \(t\)，若其向 \(x\) 写入了值 \(v\)，则写作 \(t \vdash W(x, v)\)；若其在向 \(x\) 写入之前从 \(x\) 读取了值 \(v\)，则写作 \(t \vdash R(x, v)\)。我们将事务 \(t\) 的程序顺序表示为 \(\po_t\)。
事务按照会话进行分组，每个会话是事务的一个序列。历史记录保存了客户端与数据存储系统交互的可见结果。
定义 2 历史 [Biswas and Enea 2019]
历史是一个三元组 \(\H = (T, \SO, \WR)\)，其中 \(T\) 是已提交事务的集合，\(\SO \subseteq T \times T\) 是（客户端的）会话顺序，\(\WR : \K \to 2^{T \times T}\) 是写入-读取关系，并满足：
\[ \forall t, s \in T. \forall x \in \K. t \overset{\WR(x)}{\longrightarrow} s \Rightarrow \exists v \in \V. t \neq s \wedge t \vdash \W(x, v) \wedge s \vdash \R(x, v) \]
并且
\[ \forall s \in T. \forall x \in \K . s \vdash \R(x, \_) \Rightarrow \exists! t \in T. t \overset{\WR(x)}{\longrightarrow} s \]
并且 \((\SO \cup \bigcup_{x \in \K} \WR(x))\) 无环。
请注意，历史记录仅包含已提交的事务。我们用 \(T_\otimes\) 表示数据库执行期间被中止的事务集合。如果 \(t_1 \WRxto t_2\)，我们称 \(t_2\) 从 \(t_1\) 写入的值中读取 \(x\)；当 \(x\) 不相关时，我们也可以写作 \(t_1 \WRto t_2\)。为了简便起见，我们滥用符号，将 \(\WR\) 也表示为关系 \(\bigcup_{x \in \K} \WR(x) \subseteq T \times T\)。因果顺序定义为 \(\CO \triangleq (\SO \cup \WR)^+\)，它捕捉了事务之间的潜在因果关系。我们用 \(\WT_x = \set{ t \in T \mid \exists o \in O(t). o = \W(x, \_)}\)（或 \(\RT_x = \{ t \in T \mid \exists o \in O(t). o = \R(x, \_)\}\)）表示写入（或读取）\(x\) 的事务集合。我们进一步使用 \(\WR(x)\)（或 \(\WR\)，如果 \(x\) 不相关）来表示历史中关于 \(x\) 的写入-读取关系。我们允许一个读取操作读取同一事务中写入操作写入的值。
我们基于 Biswas 和 Enea [2019] 提出的公理框架对 HAT 隔离级别进行了 TAP（事务异常模式）建模。历史符合隔离级别的定义为，存在一个会话顺序 \(\SO\)、写入-读取关系 \(\WR\) 以及事务的提交顺序，它们遵守某些公理（如下所述）。提交顺序 \(\CM \subseteq T \times T\) 是一个保持事务因果顺序的严格全序关系，即 \(\CO \subseteq \CM\)。直观地说，\(\CM\) 决定了事务在“全局”数据存储中提交的顺序。请注意，\(\CM\) 包含了众所周知的每个键的版本顺序 [Adya 1999]：假设事务 \(t\) 和 \(t'\) 都对键 \(x\) 进行了写入，当且仅当 \(t\) 写入的 \(x\) 的版本在 \(t'\) 写入的版本之前时，\(t \CMto t'\) 成立。我们将在涉及相同键写入的事务中将提交顺序和版本顺序互换使用。
Biswas 和 Enea 的框架适用于对数据库历史的黑盒隔离检查，因为 \(\SO\)、\(\WR\) 和 \(\CO\) 关系可以直接从历史中提取或推导出来，并且提交顺序可以有效地从这三个关系中推断出来（如下所述）。我们在这一正式框架内统一了四种代表性 HAT 隔离级别的定义，包括我们提出的 CI 和 RC 的新公理。这是我们后续设计细粒度 TAPs 及其正确性和完备性证明的基础。
定义 3 切断隔离 [Bailis et al. 2013a, 2016]
当且仅当以下切断隔离性公理成立时，历史 \((T, \SO, \WR)\) 满足 CI。
（切断隔离性公理）如果一个事务多次从其他事务读取同一个键，则它每次读取的值都相同。形式化表示为：
\[ \forall x \in \K. \forall v, v' \in \V. \forall t \in \RT_x. \forall t_1 \neq t, t_2 \neq t \in \WT_x. \\ \forall r_1 \triangleq \read(x, v), r_2 \triangleq \read(x, v') \in \R_x(t). \forall w_1 \in \W_x(t_1), w_2 \in \W_x(t_2). \\ (t_1 \neq t_2 \land r_1 \neq r_2 \land w_1 \wrxto r_1 \land w_2 \wrxto r_2 \Rightarrow v = v') \]
注意，当 \(t_1 = t_2\) 时，我们有一个事务中的两个写操作 \(w_1\) 和 \(w_2\) 它们写入相同的键但具有不同的值。当另一个事务从这两个写操作读取时，我们将这种场景归类为中间读取异常（TAP-f，详见 \(\S 3.2\)）。
定义 4 已提交读
当且仅当存在事务的提交顺序 \(\CM\) 满足以下四个要求时，历史 \(\H = (T, \SO, \WR)\) 满足 RC。
RC-(1) 读取操作不能读取同一事务中更晚写入的值。形式化表示为：
\[ \forall t \in T. \forall r \in \R(t). \forall w \in \W(t). w \WRto r \Rightarrow w \potto r \]
RC-(2) 在事务 \(t\) 中，如果读取操作 \(r\) 在事务 \(t\) 的写操作之后读取键 \(x\)，则它应该返回写操作写入的值。形式化表示为：
\[ \forall x \in \K. \forall t \in T. \forall r \in \R_x(t). ((\exists w' \in \W_x(t). w' \potto r) \\ \Rightarrow (\exists w \in \W_x(t). w \potto r \land w \wrxto r \land (\forall w'' \in \W_x(t), w'' \potto w \lor w'' = w \lor r \potto w''))) \]
RC-(3) 如果一个事务对同一个键进行了多次写入操作，则其他事务只能看到最后一次写入的值。形式化表示为：
\[ \forall x \in \K. \forall t \in T. \forall w, w' \in \W_x(t). \left( \exists t' \neq t \in \RT_x. \exists r \in \R_x(t') . w \wrxto r \right) \Rightarrow w' \potto w \lor w' = w. \]
RC-(4) 单调原子视图公理（MonoAtomicView） [Adya 1999; Bailis et al. 2013a]：如果两个事务 \(t_1\) 和 \(t_2\) 对 \(x\) 进行了写操作，而事务 \(t_3\) 首先从 \(t_2\) 读取了 \(y \neq x\)，然后从 \(t_1\) 读取了 \(x\)，那么 \(t_2 \CMto t_1\)。形式化表示为：
\[ \forall x, y \neq x \in \K. \forall t_1, t_2 \neq t_1 \in \WT_x. \forall t_3 \in \RT_y \setminus \{t_1, t_2\}. \\ \left( \exists w_x \in \W(t_1). \exists w_y \in \W(t_2). \exists r_x, r_y \in \R(t_3). r_y \overset{\po_{t_3}}{\longrightarrow} r_x \land w_y \overset{\wr(y)}{\longrightarrow} r_y \land w_x \overset{\wr(x)}{\longrightarrow} r_x \right) \Rightarrow t_2 \CMto t_1 \]
TODO：第 4 条公理中为什么有 \(y \ne x\) 的限制？
定义 5 读原子性（ReadAtomic）
当且仅当历史 \(\H = (T, \SO, \WR)\) 满足 RC（更具体地说，RC-(1–3)），并且存在事务的提交顺序 \(\CM\) 满足以下读原子性公理时，历史满足 RA。
（读原子性公理）如果事务 \(t_3\) 从事务 \(t_1\) 读取了键 \(x\)，并且存在另一个事务 \(t_2 \neq t_1\) 也对 \(x\) 进行了写操作且满足 \(t_2 \overset{\SO \cup \WR}{\longrightarrow} t_3\)，那么 \(t_2 \overset{\CM}{\longrightarrow} t_1\)。形式化表示为：
\[ \forall x \in \K. \forall t_1, t_2 \neq t_1 \in \WT_x. \forall t_3 \in \RT_x \setminus \{ t_1, t_2 \}. \left( t_1 \WRxto t_3 \land t_2 \overset{\SO \cup \WR}{\longrightarrow} t_3 \Rightarrow t_2 \CMto t_1 \right) \]
注意，MonoAtomicView 公理 RC-(4) 可以由 ReadAtomic 公理推出。
定义 6 事务因果一致性
当且仅当历史 \(\H = (T, \SO, \WR)\) 满足 RC（更具体地说，RC-(1–3)），并且存在事务的提交顺序 \(\CM\) 满足以下因果公理时，历史满足 TCC。
（因果公理）如果事务 \(t_3\) 从事务 \(t_1\) 读取了键 \(x\)，并且存在另一个事务 \(t_2 \neq t_1\) 也对 \(x\) 进行了写操作且满足 \(t_2 \COto t_3\)，那么 \(t_2 \CMto t_1\)。形式化表示为：
\[ \forall x \in \K. \forall t_1, t_2 \neq t_1 \in \WT_x. \forall t_3 \in \RT_x \setminus \{ t_1, t_2 \}. \left( t_1 \WRxto t_3 \land t_2 \COto t_3 \Rightarrow t_2 \CMto t_1 \right) \]
注意，RC-(4) 由因果公理隐含。TCC 的收敛性属性要求并发冲突事务在所有服务器（或副本）上以相同顺序提交。提交顺序 \(\CM\) 的存在自然反映了这一特性。
我们现在正式地将这些隔离级别联系起来（见图 1）。
定理 1：TCC 比 RA 更强，RA 比 CI 更强。
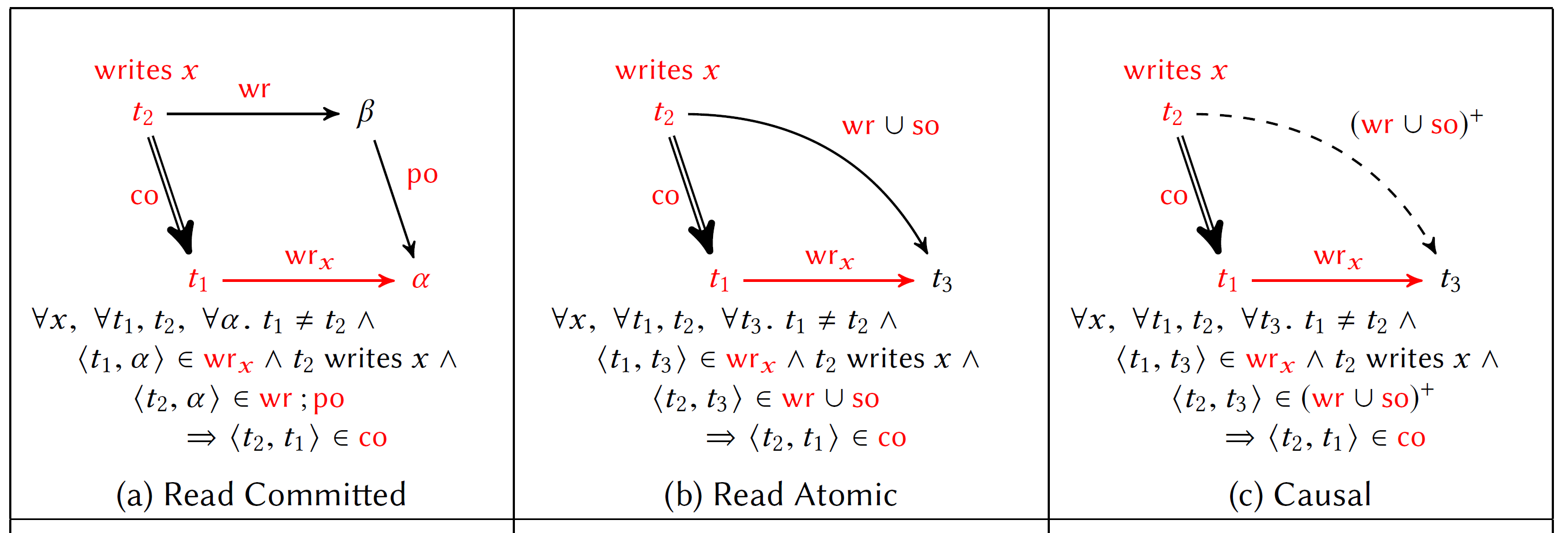
下图 [Biswas OOPLSA'19] 直观表达了上述几种隔离级别。
Transactional Anomalous Patterns
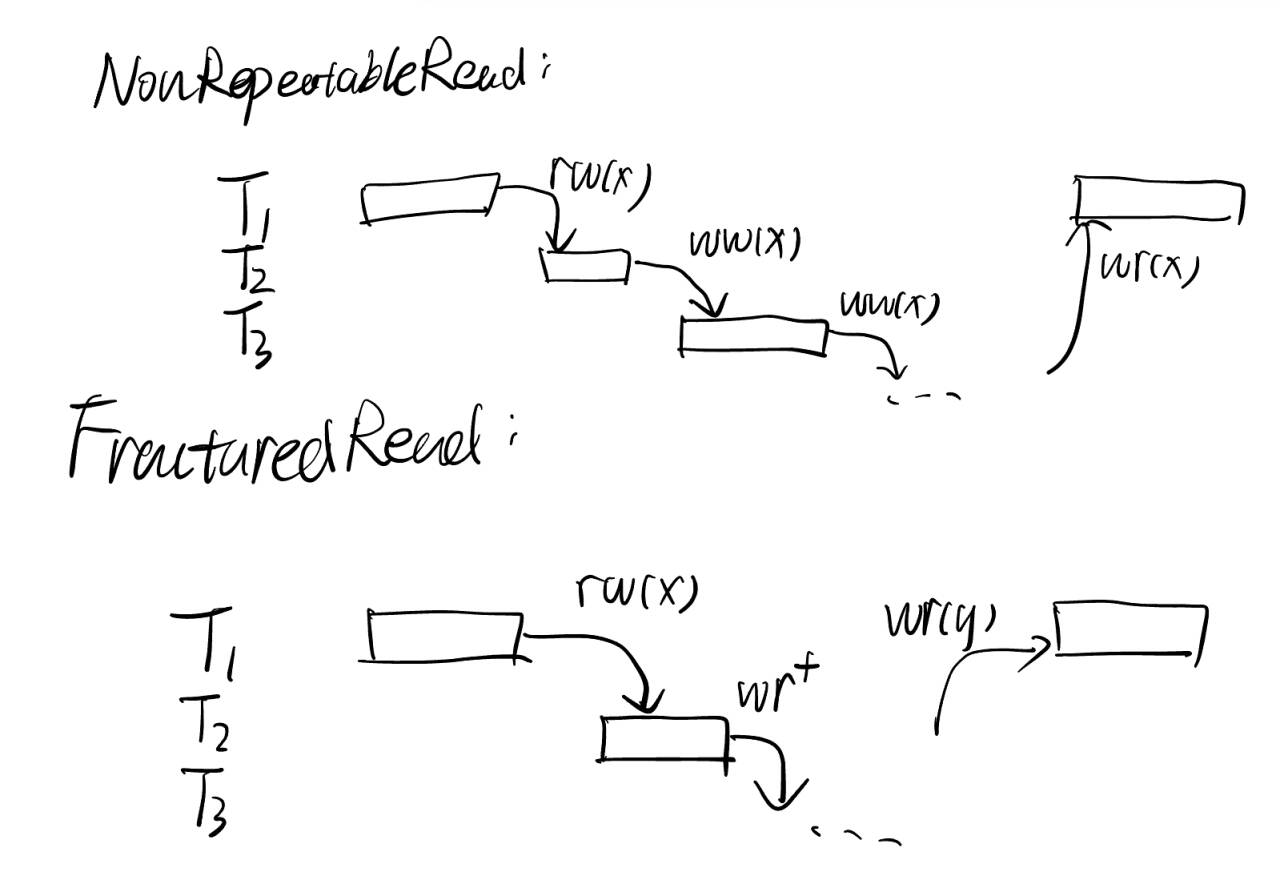
上述 TAP 的典型调度：
j: NonRepeatableRead
\[ T_1: &\R(x,1) & & R(x,2)\\ T_2: & & \W(x,2) & \]
kl: FracturedRead
\[ T_1: & & \W(x,2) \W(y,1) & \\ T_2: & \R(x,1) & & \R(y,1) \]
提取典型调度当中的特征依赖关系，即可构造每个 TAP 的“特征调度模式”
\(\set{RA 下反例调度} \setminus \set{RC 下禁止的特征调度} = \set{RC 下的反例调度}\)
理论上，在鲁棒性验证领域，可以用特征调度模式刻画所有的 TAP。只要获得依赖 TAP 定义的隔离级别，就可以判定任意两个隔离级别之间的鲁棒性。
使用细粒度 TAP 得出 HAT 隔离级别的 sound and complete 表征并非易事。虽然表征现有定义中省略的一些异常（例如中止读取 (TAP-b) 和循环因果顺序（TAP-g））相对简单（例如定义 2），但挑战在于表征所有异常以实现完整性。隔离级别的微妙语义极端情况以及它们在文献和实践中的不同解释使这项任务变得更加复杂。例如，Biswas 和 Enea [2019] 和 Bailis 等人 [2016] 对 RA 的定义不同；Elle [Kingsbury and Alvaro 2020] 检查了 Adya 的 PL-2 [Adya 1999] 中的 RC，与 dbcop [Biswas and Enea 2019] 所基于的 Biswas 和 Enea 框架不同，它不涵盖单调读取（如表 5 所示）。我们对 TAP 的设计是一个迭代过程。
我们根据 HAT 的语义构建块逐步设计 TAP。这些构建块包括提交读取、单调读取、原子可见性、事务因果关系，还涵盖事务内（例如可重复读取）和事务间（例如收敛）依赖关系。具体来说，正如我们将看到的（\(\S 5.3\)），许多最先进的隔离检查器主要是通过捕获事务间依赖关系来构建的，并且会忽略事务内异常，例如不可重复读取（MariaDB 将其标记为“关键”）。此外，我们使用文献中现有的隔离级别和一致性属性的形式化 [Adya 1999；Bailis et al 2013a；Berenson et al 1995；Biswas and Enea 2019；Bouajjani et al 2017；Cerone et al 2015；Crooks et al 2017；Xiong et al 2020] 以及在野外发现的隔离异常 [Biswas and Enea 2019；Huang et al 2023；Jepsen 2024b] 逐步完善这些 TAP。这个迭代设计过程以我们成功的形式化证明健全性和完整性（§3.3）而终止；当我们尝试的证明失败时，我们重复这个过程。
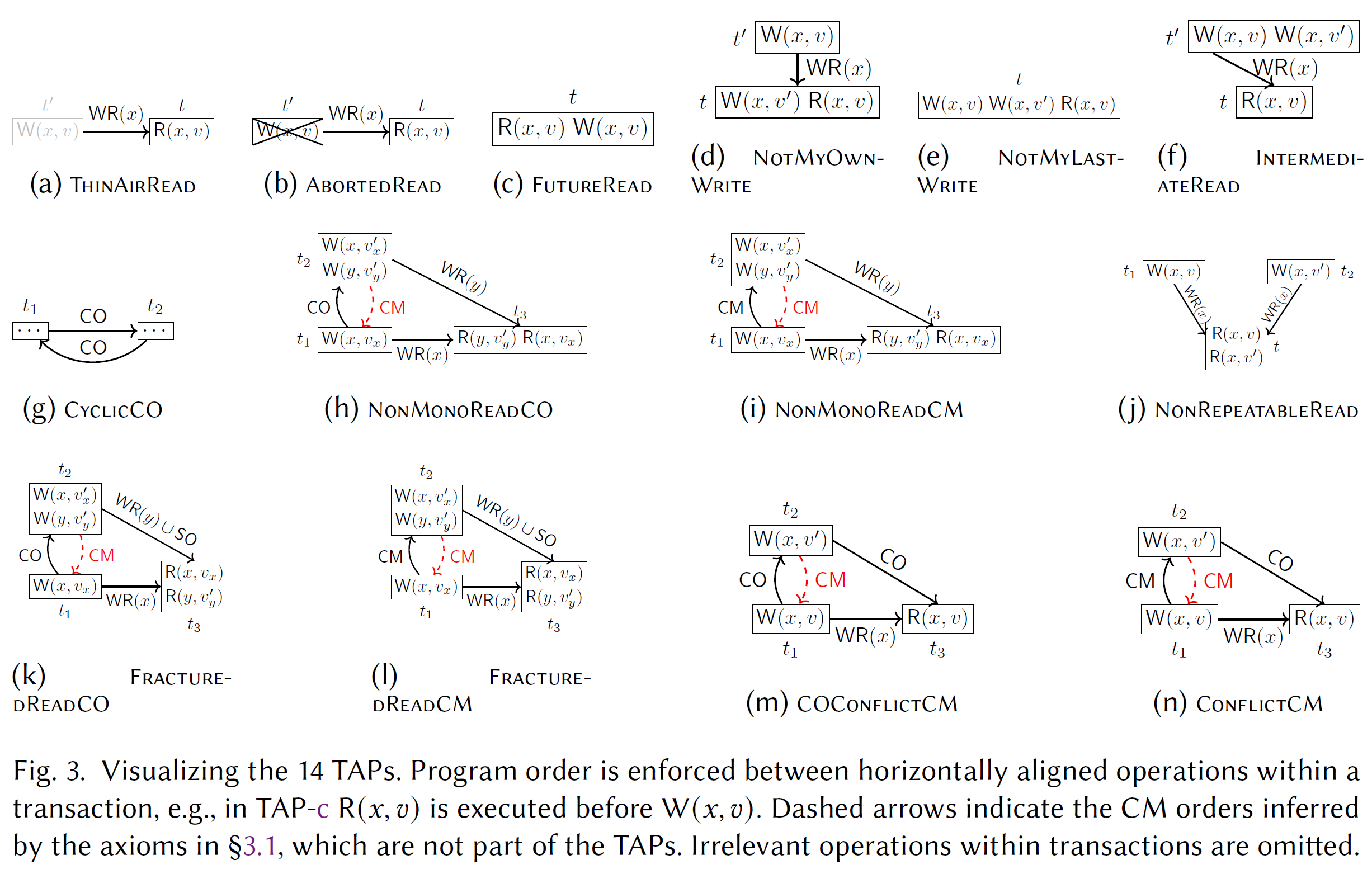
表 1 描述了我们的 14 个 TAP 及其形式化。图 3 显示了随附的可视化效果。值得一提的是，我们使用 TAP 来捕获 HAT 语义的想法受到 (i) 形式化非事务因果一致性的“坏模式”[Bouajjani et al 2017] 和 (ii) 表征隔离级别的禁止现象 [Adya 1999; Berenson et al 1995] 的启发。我们的一些 TAP 在语义上与它们的异常“重叠”，例如 [Bouajjani et al 2017] 中的循环因果顺序，以及 [Adya 1999] 中的中止或中间读取。尽管如此，这些先前的研究并没有为较新的 HAT 隔离保证（例如读取原子性和事务因果一致性）建立合理而完整的表征。相反，我们使用我们设计的 TAP 统一了各种 HAT 隔离级别的形式化。
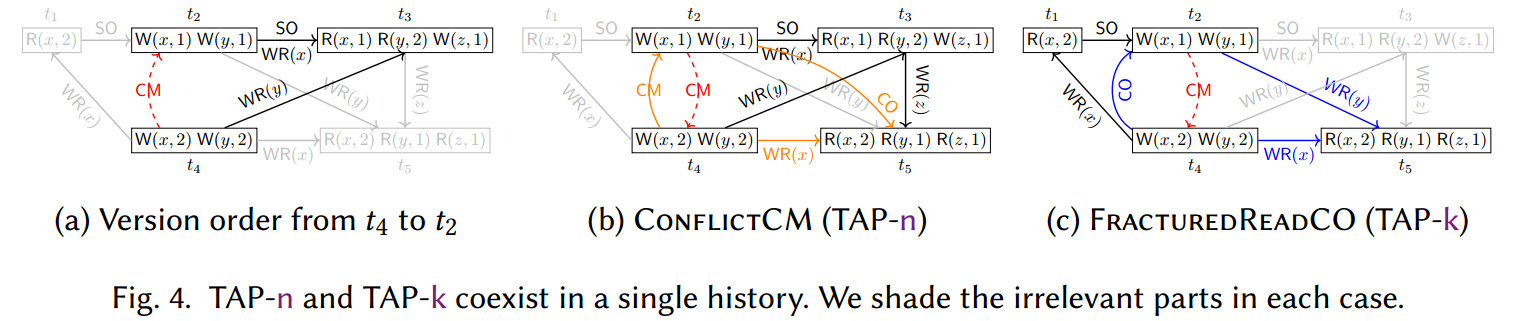
还请注意，我们的 TAP 基于 Biswas 和 Enea [2019] 的框架，其中一些可以看作是正模式的“否定”（参见 [Biswas and Enea 2019，图 2]）。例如，我们的 TAP-m 和 TAP-n 对应于它们的因果模式。对于这种情况，我们通过区分版本顺序冲突来细化否定，例如通过因果传递依赖关系（TAP-m）或收敛（TAP-n）。这为用户提供了对违规行为的更深入的了解，因为这些属性通常是通过不同的机制开发的，例如，因果关系的逻辑时间戳与数据收敛的冲突解决相反 [Liu et al. 2024b; Lloyd et al 2013]。
TODO：RA 相比于 RC 多禁止的异常（jkl）当中，哪些是意料之外的？
The Checking Algorithm
Overview
Algorithm
Optimization with Tree Clocks
Time Complexity
Experiments
Workloads, Benchmarks, and Setup
Detecting Isolation Bugs
Finding All Anomalies
Understanding Violations Found
Related Work
Characterizing Database Isolation
随着可靠、高可用性数据库事务设计方面的进步，人们投入了大量精力 [Adya 1999; Bernstein et al 1979; Biswas 和 Enea 2019; Cerone et al 2015; Crooks et al 2017] 来形式化隔离保证。Cerone et al [2015] 提出了一个框架，用于声明性地指定至少与读取原子性一样强的隔离级别，具有可见性（事务可以观察到的内容）和仲裁（在我们的案例中是提交顺序）的双重概念。我们基于 TAP 对 HAT 隔离级别的描述基于 Biswas 和 Enea [2019] 提出的替代公理框架。该框架更适合黑盒测试，因为可以自然地从历史记录中提取写入-读取关系（扮演可见性关系的角色 [Cerone et al 2015]）以及会话顺序。 我们也受到了先前研究 [Adya 1999; Berenson et al 1995; Bouajjani et al 2017] 的启发，他们秉承同样的精神，使用异常来表征隔离/一致性标准。然而，Berenson et al [1995] 和 Adya [1999] 没有涵盖较新的隔离级别，例如读取原子性和 TCC；Bouajjani et al [2017] 仅考虑（非事务性）因果一致性。我们通过合理而完整地表征弱 HAT 隔离级别来补充这方面的研究。
最近，Crooks et al [2017] 和 Xiong et al [2020] 通过客户端可观察状态引入了隔离级别的替代形式化。一个悬而未决的问题是，它们是否会产生更有效的隔离检查算法。
Black-box Checking Isolation
我们专注于最先进的数据库隔离黑盒检查器，从而排除了依赖白盒方法的工作 [Clark et al 2024; Liu et al 2019b]。我们使用 SIEGE+ [Huang et al 2023] 检查这些黑盒检查器（另见 $$5），如表 6 所示。
Plume 满足所有 SIEGE+ 标准，重点是完整和有效的异常检测，正如我们的评估所证明的那样。除了 Elle-TCC 可能报告误报（即丢失的更新）之外，其他检查器都是可靠的（没有误报）和有效的（在真实数据库中发现错误）。 CausalC 专注于因果一致性，不支持一般交易。基于求解器的工具（如 Viper 和 Cobra）通常会返回难以理解的反例，例如未满足的条款。
PolySI 通过从未满足的条款构建违规场景来改进它们。尽管 dbcop 也利用图遍历来搜索隔离错误，但其当前实现仅返回“真”（无错误）或“假”（发现错误）。这对于理解错误是如何发生的没有帮助。相比之下，Elle 和 Plume 分别就 Adya 的异常和 TAP 实例报告了详细的违规场景。此外，正如我们的实验结果所示，Plume 的表现明显优于 dbcop，以及利用基于答案集编程和高级 MonoSAT 求解器的各种求解技术的强大基线。在具有更高并发性的大型工作负载（例如，更多客户端）下，Plume 的表现也优于 Elle。除 PolySI 之外的其他检查器都错过了 HAT 隔离异常，尽管其中一些检查器是为检查更强的隔离标准而设计的。所有检查器都可以处理读写寄存器。Plume 和 Viper 也与 Elle 一起支持列表附加历史记录。此外，Viper 可以处理特定类型的范围查询，其中范围指的是键，而不是值。
Discussion
Beyond HAT Isolation
正如我们所观察到的，许多声称提供更强隔离保证的数据库实际上违反了更弱的 HAT 隔离保证。这表明使用 Plume 进行首次分析可能是有效的，更重要的是，它效率很高，因为它可以在几分钟内快速检查数百万笔交易。
Plume 利用向量和树时钟的关键思想可以适用于其他基于图的方法来检查更强的隔离保证。这将加速各种依赖图的遍历，例如多图 [Papadimitriou 1979]（由 Cobra、PolySI 和 Viper 采用）和 Adya 的直接序列化图 [Adya 1999]（由 Elle 采用）。具体来说，对于只有更强的隔离级别 𝐿（例如快照隔离）才能禁止的异常（例如丢失更新），有必要设计新的 TAP。除了现有的 TAP（由于其模块化），还必须建立对 𝐿 的合理和完整的表征。我们将这组结果 TAP 表示为 𝑆。
然后可以应用向量和树时钟来检查 𝐿。检查 𝐿 时的主要区别在于需要“猜测”写入的版本顺序（以及相关事务）。考虑来自两个不同事务的 𝑊1 和 𝑊2，它们都写入同一个密钥。新的检查算法首先假设在构建依赖关系图期间 𝑊1 排在 𝑊2 之前，并在 𝑆 中搜索任何 TAP。如果找到 TAP，算法将切换到替代版本顺序并再次在 𝑆 中搜索任何 TAP。对于每个猜测，可以以与 Plume 中相同的方式使用向量和树时钟。如果在两种情况下都识别出 TAP，则历史记录违反 𝐿。
Beyond Database Engines
到目前为止，我们一直专注于检查数据库引擎中的隔离保证。许多数据库支持的应用程序（例如社交网络和电子商务）也提供了较弱的 HAT 语义，并且已知会出现数据异常 [Gan et al 2020; Warszawski and Bailis 2017]。此外，我们还看到 HAT 语义（例如 RA 和 TCC）被有前途的计算架构采用，例如无服务器计算 [Lykhenko et al 2021; Wu et al 2020] 和微服务 [Ferreira Loff et al 2023; Pereira and Silva 2023]。由于 Plume 具有黑盒特性，因此可以自然地应用于检测这些应用领域中的隔离违规。只需要以局外人的身份收集系统执行历史记录，然后将其提供给 Plume。
Limitations and Future Work
Plume 可能会遗漏 HAT 语义未涵盖的错误，例如丢失更新和写入偏差 [Cerone et al 2015; Liu et al 2019a]。Plume 也无法处理范围查询，为此我们计划探索应用墓碑 [Zhang et al 2023]（Viper 采用此方法检查 SI）和 SQL 级检测 [Jiang et al 2023]（TxCheck 设计此方法用于检测逻辑数据库错误）的可能性。包括 Plume 在内的所有黑盒隔离检查器都依赖于随机生成大型工作负载或测试用例（图 2 中的步骤 ①）。但是，正如我们所观察到的，像图 7 中的反例通常比生成的工作负载小得多。设计简洁而有效的测试用例将提高整体检查性能。
Conclusion
Plume 是第一个高效、完整的弱隔离级别黑盒检查器。它补充了两条研究路线：在理论层面，通过异常来表征数据一致性；在实践层面，设计高性能的黑盒隔离检查器。对于提供多个隔离级别的数据库，可以自然地使用 Plume 和前面提到的检查器（例如 PolySI）分别检查弱级别和强级别。这归因于这些检查器的黑盒性质，它们以基本相同格式的历史记录作为输入。我们将 Plume 以及几个强隔离级别检查器集成到我们的数据库隔离检查系统 IsoVista [Gu et al 2024] 中，该系统具有用户友好的界面。此外，Plume 的信息性反例可以促进调试并帮助开发人员重新思考他们的系统设计和实现。我们的 TAP 和测试用例也可以帮助巩固隔离检查器的开发。我们希望这项工作也能为检查数据库以外的数据一致性提供启示。
Acknowledgments
我们感谢匿名审阅者的宝贵反馈。我们还要感谢 Zihe Song 在识别 MariaDB-Galera 中的隔离错误方面做出的贡献。刘思获得了苏黎世联邦理工学院职业种子奖的支持。
