$$ \def\po{\mathsf{\textcolor{\red}{po}}} \def\so{\mathsf{\textcolor{\purple}{so}}} \def\wr{\mathsf{\textcolor{\teal}{wr}}} \def\co{\mathsf{\textcolor{\orange}{co}}} \def\Swap{\mathsf{Swap}} $$
摘要
现代应用程序,如社交网络系统和电子商务平台,以大规模数据库为核心,用于存储和检索数据。对数据库的访问通常封装在事务中,允许对共享数据进行的计算与其他并发计算隔离,并具有容错性。现代数据库以性能为代价来交换隔离程度。隔离级别越低,数据库允许表现出的行为就越多,而开发人员需要确保他们的应用程序能够容忍这些行为。
在这项工作中,我们提出了一种基于动态偏序约减的无状态模型检查算法,用于研究依赖于多种常见弱隔离级别的应用程序的正确性,包括读已提交、因果一致性、快照隔离和可串行化。我们展示了这些算法在所有情况下都是完备的、正确的和最优的,并且在所有情况下都具有多项式内存消耗。我们报告了这些算法在 Java Pathfinder 环境中的实现,应用于分布式系统和数据库文献中的一些具有挑战性的应用程序。
作者:
- AHMED BOUAJJANI, Université Paris Cité, CNRS, IRIF, France
- CONSTANTIN ENEA, LIX, Ecole Polytechnique, CNRS and Institut Polytechnique de Paris, France
- ENRIQUE ROMÁN-CALVO, Université Paris Cité, CNRS, IRIF, France
INTRODUCTION
数据存储不再是将数据写入具有单点访问的单个磁盘。现代应用程序不仅需要数据可靠性,还需要高吞吐量的并发访问。涉及供应链、银行等的应用程序使用传统的关系数据库来存储和处理数据,而社交网络软件和电子商务平台等应用程序则使用基于云的存储系统(例如 Azure Cosmos DB [Paz 2018]、Amazon DynamoDB) [DeCandia et al. 2007]、Facebook TAO [Bronson et al. 2013] 等)。
不幸的是,提供高吞吐量处理的代价是不可避免地削弱为用户提供的一致性保证:并发连接的客户端可能最终会观察到同一数据的不同版本。这些“异常”可以通过使用强大的隔离级别来防止,例如可串行化[Papadimitriou 1979],它本质上在任何时间点向所有客户端提供单一版本的数据。然而,串行化需要昂贵的同步并且会带来很高的性能成本。因此,大多数存储系统使用较弱的隔离级别,例如因果一致性 [Akkoorath and Bieniusa 2016; Lamport 1978; Lloyd et al. 2011],快照隔离 [Berenson et al. 1995],阅读提交 [Berenson et al. 1995]等以获得更好的性能。在最近的一项数据库管理员调查中 [Pavlo 2017],86% 的参与者表示,他们数据库中的大部分或全部事务都在读提交级别执行。
较弱的隔离级别比较强的隔离级别允许更多可能的行为。然后,开发人员需要确保他们的应用程序能够容忍这一更大的行为集。不幸的是,弱隔离级别很难理解或推理 [Adya 1999; Brutschy et al. 2017] 以及由此产生的应用程序错误可能会导致业务损失 [Warszawski and Bailis 2017]。
Model Checking Database-Backed Applications
- Model Checking(模型检查):会导致状态爆炸
- POR(偏序约减):在不牺牲覆盖率的情况下,通过合并等价类减少搜索状态
- OPOR(最优 POR):每个等价类选择一个状态
- DPOR(动态 POR):在不依赖于静态分析的情况下实时探索执行空间(并跟踪执行之间的等价关系)
- SMC(无状态模型检查):探索程序的执行而不存储访问过的状态,从而避免了过多的内存消耗
以前的工作:弱内存模型下的共享内存程序 DPOR;soundness & completeness,但是 optimal 指数空间复杂度;Kokologiannakis et al. [2022] 定义了一种具有多项式空间复杂度的 DPOR 算法,并且是健全的、完整的和最优的。该算法可应用于一系列共享内存模型。
本文的贡献:针对在弱隔离级别下运行的数据库事务程序提出了依赖 DPOR 技术的新无状态模型检查算法。
本文解决了针对给定隔离级别的模型检查代码正确性的问题。模型检查 [Clarke et al. 1983; Queille and Sifakis 1982] 以系统的方式探索给定程序的状态空间,并提供了程序行为的高覆盖率。然而,它面临着臭名昭著的状态爆炸问题,即执行数量随着并发客户端数量呈指数增长。
偏序约简(POR)[Clarke et al. 1999; Godefroid 1996; Peled 1993; Valmari 1989] 是一种在不牺牲覆盖范围的情况下限制探索执行数量的方法。POR 依赖于执行之间的等价关系,例如,如果可以通过交换连续的独立(不冲突)执行步骤从另一个执行获得一个执行,则两个执行是等效的。它保证至少探索每个等价类的一个执行。最佳 POR (Optimal POR)技术只探索每个等价类的一次执行。除了这种经典的最优性概念之外,POR 技术还可以通过避免访问阻止探索的状态来实现最优性。引入动态偏序约简(DPOR)[Flanagan and Godefroid 2005] 来动态探索执行空间(并跟踪执行之间的等价关系),而不依赖于先验静态分析。这通常与无状态模型检查(SMC)[Godefroid 1997] 相结合,它探索程序的执行而不存储访问的状态,从而避免过多的内存消耗。
有大量关于 (D)POR 技术的工作,这些技术在检查某类程序的某类规范时解决了它们的健全性,以及它们的完整性和理论最优性(参见第 8 节)。大多数情况下,这些工作考虑在强一致性内存模型下执行的共享内存并发程序。
在过去的几年中,一些工作研究了在弱内存模型(例如 TSO 或 Release-Acquire)下运行的共享内存程序的 DPOR。[Abdulla et al. 2017a, 2016, 2018; Kokologiannakis et al. 2019]。虽然这些算法是合理且完整的,但当它们最优时,它们具有指数空间复杂度。最近,Kokologiannakis et al. [2022]定义了一种具有多项式空间复杂度的 DPOR 算法,并且是健全的、完整的和最优的。该算法可应用于一系列共享内存模型。
虽然上面提到的工作涉及共享内存程序,但我们不知道有任何已发表的工作解决在弱隔离级别下运行的数据库事务程序的情况。在本文中,我们解决了这种情况,并针对数据库支持的应用程序提出了依赖 DPOR 技术的新无状态模型检查算法。我们假设应用程序中的所有事务都在相同的隔离级别下执行,这在实践中经常发生(如上所述,大多数数据库应用程序都在数据库的默认隔离级别上运行)。我们的工作概括了 [Kokologiannakis et al. 2022]等人提出的方法。然而,这种对事务案例的概括(涵盖最相关的隔离级别)并不是 [Kokologiannakis et al. 2022] 的直接改编,在保留其他属性(例如完整性和多项式内存复杂性)的同时确保最优性是非常具有挑战性的。接下来,我们解释一下我们工作的主要步骤和特点。
Formalizing Isolation Levels
我们的算法依赖于 Biswas 和 Enea [2019] 引入的隔离级别的公理定义。这些定义使用称为公理的逻辑约束来表征符合特定隔离级别(可扩展为 SQL 查询 [Biswas et al. 2021])的数据库执行集(例如键值存储)。这些约束指的是执行中事件/事务之间的一组特定关系,描述控制流或数据流依赖性:同一事务中的事件之间的程序顺序 $\po$,同一会话中的事务之间的会话顺序 $\so$,以及 写-读 $\wr$(读取)关系,将每个读取事件与写入读取返回的值的事务关联起来。这些关系以及执行中的事件被称为历史 history。历史记录仅描述与数据库的交互,省略应用程序端事件(例如,写入数据库的计算值)。
Execution Equivalence
DPOR 算法通过执行上的等价关系进行参数化,最常见的是 Mazurkiewicz 等价 [Mazurkiewicz 1986]。在这项工作中,我们考虑了一种较弱的等价关系,也称为读取等价 [Abdulla et al. 2019, 2018; Chalupa et al. 2018; Kokologiannakis et al. 2022, 2019; Kokologiannakis and Vafeiadis 2020],它认为当两个执行的历史完全相同时(它们包含相同的事件集,并且关系 $\po$、$\so$ 和 $\wr$ 相同),则两次执行是等价的。一般来说,等价读取比 Mazurkiewicz 等价更粗糙,并且在某些情况下,其等价类可以指数小于 Mazurkiewicz 迹线 [Chalupa et al. 2018]。
SMC Algorithms
- sound:枚举的都是合法的
- complete:枚举覆盖每个等价类
- optimal:每个等价类仅选择一个执行
我们的 SMC 算法枚举给定隔离级别 $I$ 下给定程序的执行情况。它们是健全的(sound),即,仅枚举可行的执行(被承认为 $I$ 下的程序),完整的(complete),即,它们输出每个读取等价类的代表,并且是最佳的(optimal),即,它们从每个读取中准确输出一个完整的来自等价类的执行。对于因果一致性以及更弱的隔离级别,它们满足强最优性的概念,即此外,枚举避免了执行被“阻止”的状态,即它不能扩展到程序的完整执行。对于快照隔离性和可串行性,我们表明在同一类中不存在任何算法(将在下面讨论)可以确保如此强大的最优性概念。我们提出的所有算法都是多项式空间,这与许多文献中介绍的 DPOR 算法相反。
作为起点,我们定义了一类通用的 SMC 算法,称为基于交换(swapping based),泛化了 [Kokologiannakis et al. 2022, 2019],其中后者枚举了程序执行的历史记录。这些算法侧重于与数据库的交互,假设事务中的其他步骤涉及仅在封闭会话范围内可见的局部变量。执行根据通用调度程序函数 Next 进行扩展,每个读取事件都会产生多个探索分支,一个分支对应于过去执行的每个可以读取的写入。执行中的事件可以交换以产生新的探索“根源(root)”,从而导致不同的历史。为了完整性,需要交换事件,以枚举读取 A 从由 Next 在 A 之后安排的写入 F 读取的历史记录。为了确保健全性,我们限制交换的定义,以便它产生通过构造可行的历史记录(扩展可能不可行的执行可能会违反健全性)。这样的算法是最优的。当它只枚举每个历史一次时的读取等效性。
我们在此类中定义了一个具体的算法,特别是对于每个前缀封闭且因果可扩展的隔离级别(例如,读提交和因果一致性),满足上面提到的更强的最优性概念。前缀闭包意味着满足 $I$ 的历史记录的每个前缀,即交易的子集及其因果关系中的所有前驱,即 $(\so \cup \wr)^+$,也与 $I$ 一致,并且因果可扩展性意味着任何待处理事务的一个满足 $I$ 的历史可以通过再扩展一个事件来仍然满足 $I$,并且如果这是一个读取事件,则它可以从因果关系中位于其之前的事务中读取。为了确保强最优性,该算法使用精心选择的条件来限制事件交换的应用,这使得完整性证明变得非常重要。
我们表明,诸如快照隔离和可串行化之类的隔离级别不可因果扩展,并且不存在这样的基于交换的 SMC 算法,同时是健全的、完整的和强优化的(独立于内存消耗范围)。这种不可能性证明使用一个程序来表明任何 Next 调度程序和对交换的任何限制都会违反完整性或强最优性。然而,我们定义了先前算法的扩展,它满足较弱的最优性概念,同时保留健全性、完整性和多项式空间复杂性。该算法将简单地根据较弱的前缀封闭和因果可扩展的隔离级别枚举执行,并在最后输出之前根据更强的隔离级别快照隔离和可串行性过滤执行。
我们在 Java Pathfinder (JPF) 模型检查器中实现了这些算法 [Visser et al. 2004],并根据分布式系统和数据库文献中的一些具有挑战性的数据库支持的应用程序对它们进行了评估。
我们的贡献和大纲如下:
- 第 3 节确定了一类称为前缀关闭和因果可扩展的隔离级别,这些隔离级别允许有效的 SMC。
- 第 4 节定义了一类基于交换的 SMC 算法,这些算法基于 DPOR,它把给定的隔离级别作为参数。
- 第 5 节定义了基于交换的 SMC 算法,该算法对于任何前缀封闭且因果可扩展的隔离级别来说都是健全的、完整的、强最优的、多项式空间的。
- 第 6 节说明了对于快照隔离和可串行化等隔离级别,不存在基于交换的算法,它在同一时间既是健全的、完整的,又是强优化的,并提出了一个基于交换的算法,该算法满足“普通”优化性。
- 第 7 节报告了这些算法的实施和评估。
- 第 2 节回顾了 [Biswas and Enea 2019; Biswas et al. 2021] 引入的隔离级别的形式化,而第 8 和第 9 节则总结了相关工作并作出了结论性的评论。有关更多的形式化、证明和实验数据,请参见技术报告 [Bouajjani et al. 2023a]。
TRANSACTIONAL PROGRAMS
Program Syntax

图 1 列出了一种简单编程语言的定义,我们用它来表示在数据库之上运行的应用程序。 程序是一组并行运行的会话(sessions),每个会话由一系列事务(transactions)组成。 每个事务都由开始(begin)和提交(commit)或中止(abort)指令分隔,其主体包含访问数据库和操作一组本地变量的 Lvar 的指令。 我们使用符号 a、b 等来表示 Lvar 的元素。
为简单起见,我们将数据库状态抽象为对一组全局变量 Vars 的 valuation,范围使用 x、y 等。访问数据库的指令对应于读取全局变量的值并将其存储到局部变量 a 中 ($a := read(x)$) ,将局部变量 a 的值写入全局变量 x($write(x, a)$),或对局部变量 a 赋值 ($a := e$)。 全局或局部变量的值集用 Vals 表示。 对局部变量的赋值使用局部变量上的表达式 e,这些表达式被解释为值并且其语法未指定。 这些指令中的每一个都可以通过一组局部变量 $\phi(\vec{a})$ 上的布尔条件 $\vec{a}$ 来保护(它们的语法并不重要)。 我们的结果假设有界程序,就像 SMC 算法中常见的那样,因此,我们省略了 while 循环等其他结构。 操作关系表的 SQL 语句(SELECT、JOIN、UPDATE)可以编译为读取或写入表示表中行的变量(例如,参见 [Biswas et al. 2021;Rahmani et al. 2019])。
Isolation Levels
我们提出了 Biswas 和 Enea [2019] 引入的用于定义隔离级别的公理框架。 隔离级别被定义为历史上的逻辑约束(称为公理),它是执行中程序与数据库之间交互的抽象表示。
Histories
一些记号:
- event $\langle e, type \rangle$:五种事件(event):begin, commit, abort, read(x) for reading the global variable x, and write(x, v)
- trasaction log $\langle t, E, \po_t \rangle$:
- $E=\mathsf{events}(t)$
- $\po$ 是程序 body 中的 instr 全序
- pending/complete:无/有 commit 和 abort
- committed/aborted:包含 commit/abort
- reads(t):受其他事务(前驱事务)影响的读事件集合
- writes(t):本事务中未被覆盖且未被回滚的写事件集合
所有隔离级别的特点:
- 对 x 先写后读,读的结果一定是最近的之前的写的结果(即,数据库的持久性)
- 一个事务对 x 多次写,只有最后一次对其他事务可见(即,不允许脏读)
history 包含一些事务,事物之间的关系是同一个 session 内的偏序 $\so$,此外还包括 write-read 关系 $\wr$。
Axiomatic Framework
历史 history 符合某一隔离级别,当且仅当在所有事务之间有一个严格全序 $\co$,即 commit order。$\co$ 扩展了 $\so \cup \wr$,并且满足特定条件,这些条件叫做公理。公理可用如下一阶谓词表示:
$$ \forall x, \forall t_1 \neq t_2, \forall t_3. \ \langle t_1, t_3 \rangle \in \wr_x \land t_2 \mathsf{writes} x \land \phi(t_2, t_3) \Rightarrow \langle t_2, t_1 \rangle \in \co $$
这一公理含义如下:为了保证 $t_3$ 读到的确实是 $t_1$ 写的数据,所有和 $t_3$ 满足某种关系的 $t_2$ 必须在 $t_1$ 之前被提交。
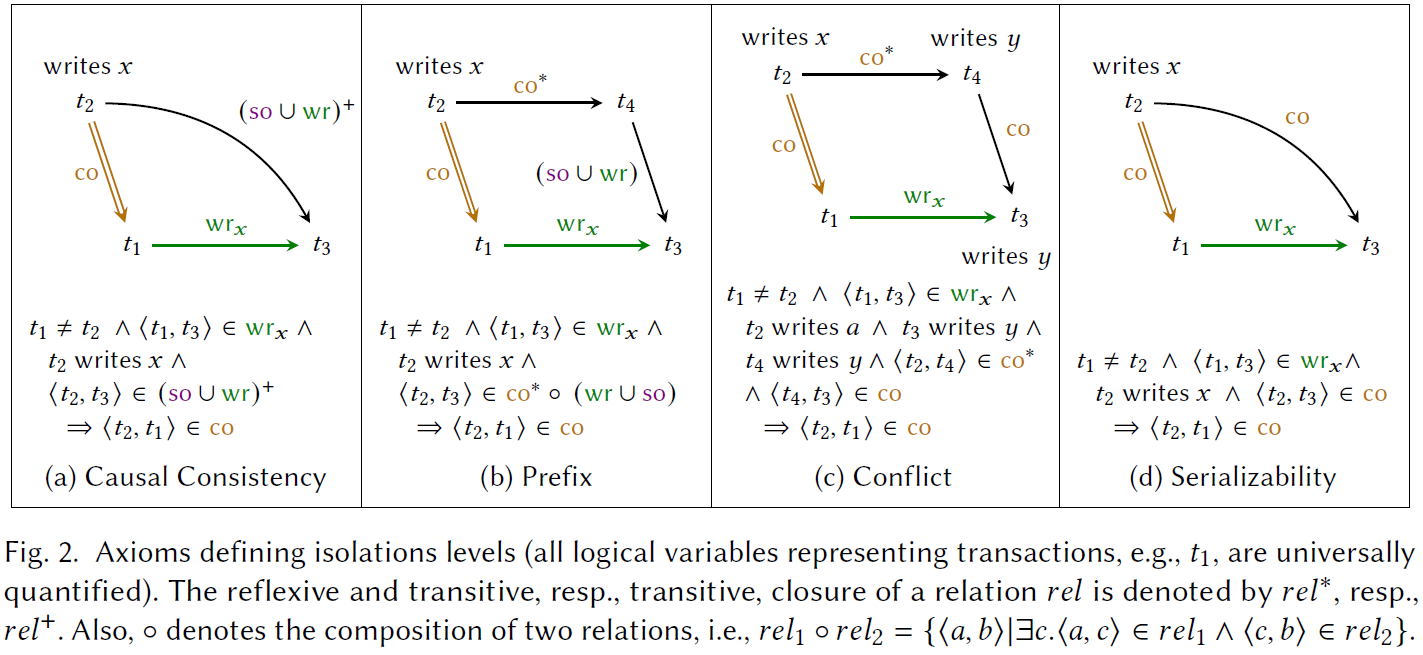
上图展示了 Casual Consistency 和 Serializablity 两种一致性的公理。另外,Prefix 和 Conflict 共同定义了 Snapshot Isolation。Read Atomic 是 CC 把 $(\so \cup \wr)^+$ 换成 $\so \cup \wr$ 的弱化版。Read Committed 定义类似。
显然,一致性强度有:$\sf{SER>SI>CC>RA>RC}$。
下图是更完整的对隔离级别的公理定义[^Biswas]。

对图片的理解:根据现有图中的 $\wr$ 边和 $\so$ 边(对于 RC,还有 $\po$ 边)推断出 $\co$ 边并加入到图中。如果加边后的图中有环,则该执行历史不符合对应的隔离级别。
可以看出,RC 中 $\alpha$ 和 $\beta$ 读到的结果可能是不一样的,即 RC 允许不可重复读。
Program Semantics
一些记号:
- 部分函数 $\mathsf{P:SessId \rightharpoonup Sess*}$,从会话 id 到具体代码
- 部分函数 $\mathsf{\so:SessId \rightharpoonup Tlogs*}$,从会话 id 到所有可能的事务日志序列的集合
- 两个事务被 $\so$ 排序意味着在某个序列 $\so(j)$ 中,一个在另一个之前。
具体来说,对于一个会话标识符 $j \in \textsf{SessId}, \so(j)$ 是一个事务日志序列,其中包含了会话 j 中执行的所有事务。
状态 configuration 之间有传递关系 $\Rightarrow_I$。其中 configuration 的定义包括:
- 历史 h 存储之前执行的数据库操作的事件;
- 值映射 $\vec\gamma$ 记录每个会话当前事务中局部变量的值(从 SessId 到局部变量的值);
- 映射 $\vec{B}$ 存储每个活动事务的代码;
- 原始程序中剩余未执行的会话/事务 P。
程序 P 在隔离级别 I 下的一个执行是一个 configuration 序列 $c_0 c_1 \dots c_n$,其中 $c_0$ 是初始 configuration,并且 $c_m \Rightarrow_I c_{m+1}$。我们说 $c_n$ 是从 $c_0$ I-reachable 的。整个执行的历史就是 $c_n$ 的历史 h。$\mathsf{P}=\empty$ 的被称为 final configuration。$\mathsf{hist}_I(\mathsf{P})$ 表示 P 在隔离级别 I 下的以 final configuration 结束的所有执行的历史。
PREFIX-CLOSED AND CAUSALLY-EXTENSIBLE ISOLATION LEVELS
我们定义了隔离级别的两个属性,前缀闭包和因果扩展性,这使得高效的 DPOR 算法成为可能(如第 5 节所示)
Prefix Closure
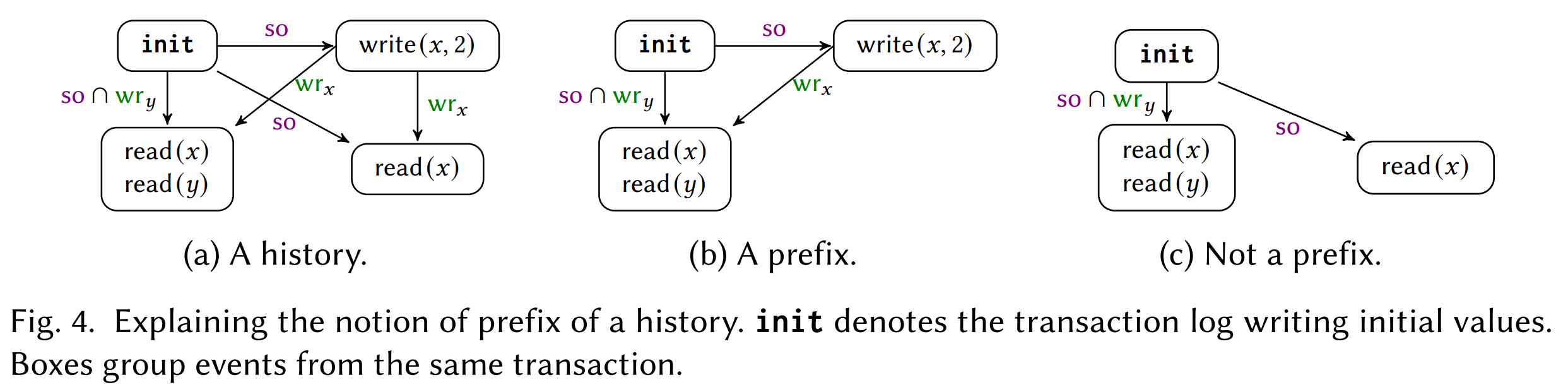
上图中,b 是 a 的前缀,而 c 不是 a 的前缀。
对于隔离级别 I,某历史 h 符合 I,则该历史的所有前缀都符合 I,则 I 有性质 Prefix Closure。
$\mathsf{RC, RA, CC, SI, SER}$ 都是 prefix closed。
Causal Extensibility
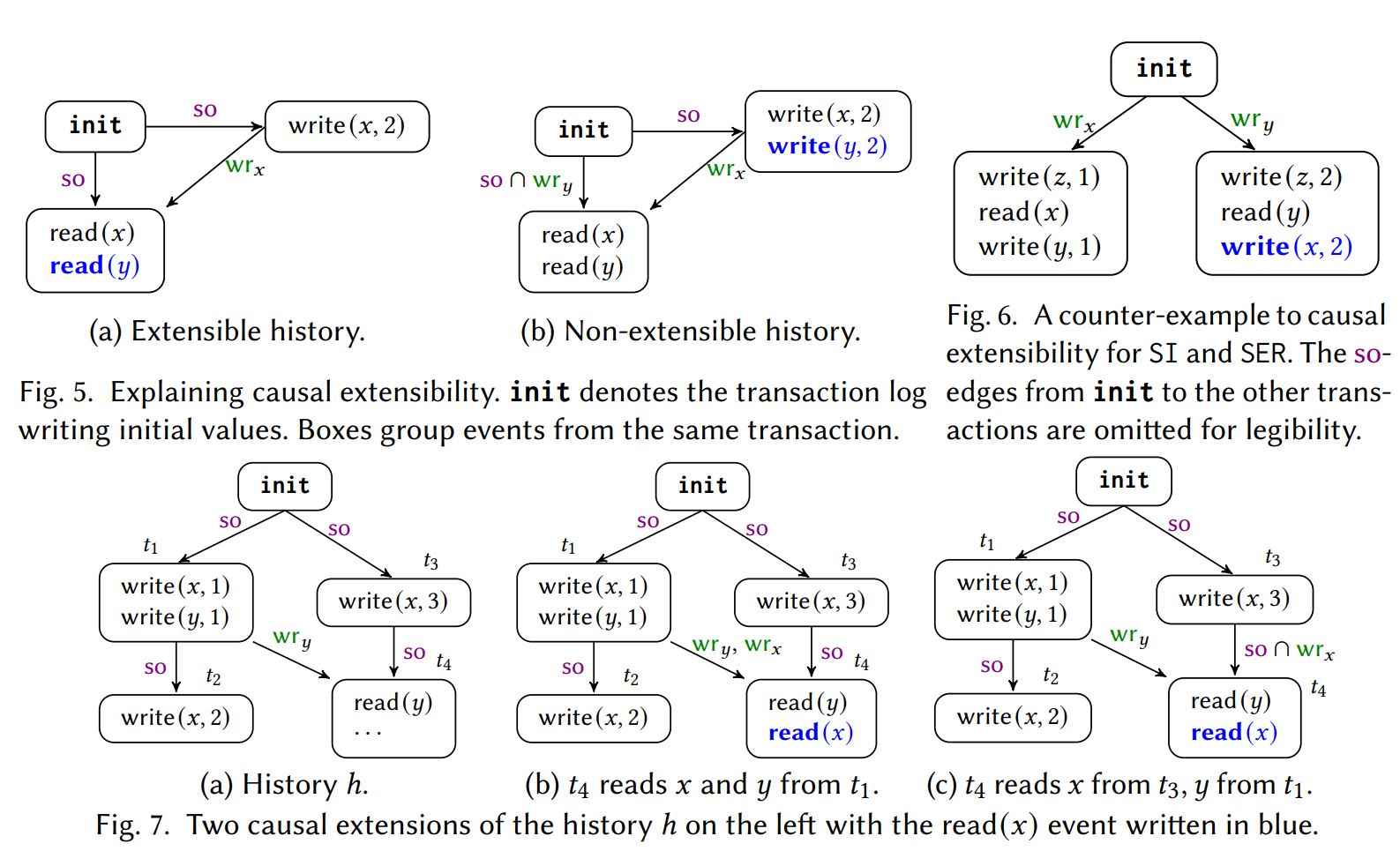
图 5 中,a 可扩展蓝色事件,b 不可扩展蓝色事件。
Causal Extensibility 是一种隔离级别的属性,指当一个历史记录是该隔离级别一致的时,它的任何因果扩展也是该隔离级别一致的。在该文献中,Causal Extensibility 是用于定义一类隔离级别,即 causally-extensible 隔离级别,这些隔离级别具有该属性,并且可以使用 DPOR 算法进行高效的状态空间缩减。
$\mathsf{CC, RA, RC}$ 是 causally-extensible;$\mathsf{SI, SER}$ 不是 causally-extensible。
同时满足以上两种性质的一致性:$\mathsf{CC, RA, RC}$。
SWAPPING-BASED MODEL CHECKING ALGORITHMS

参数含义:
- P:program;
- $h_<$:有序历史,包含了所有的 events 并用全序 < 连接;
- locals:把 event e 映射到 local variables 在 e 执行时的值 valuation。
函数 explore 首先调用 Next 来获取代表 P 的某个待处理事务中的下一个数据库访问的事件,或者用于开始或结束事务的开始/提交/中止事件。
该事件与某个会话 j 相关联。 例如,Next 的典型实现将选择一个待处理事务(在某个会话 j 中),执行所有本地指令,直到该事务中的下一个数据库指令(应用转换规则 if-true、if-false 和 local) 并返回该数据库指令对应的事件 e 和当前本地状态 $\gamma$。
如果程序结束,Next 还可以返回 $\perp$。 如果 Next 返回 $\perp$,则函数 Valid 可用于在输出当前历史记录和本地状态之前过滤满足预期隔离级别的执行(Valid 的使用将在第 6 节中变得相关)。

exploreSwaps 函数调用 ComputeReordrings 从 $h_<$ 中找到了所有的应该被交换的事务序列 $\alpha, \beta$。其中:
- $\alpha$ 在 $\beta$ 之前结束;
- $\alpha$ 包含一个 r 而 $\beta$ 包含一个相应的 w 操作,因此交换后的 $\alpha$ 和 $\beta$ 有 $\wr$ 关系;
- Optimality 函数判定 $\alpha, \beta$ 之前没有被交换过。
交换之后,对交换后的历史 $h'< = \Swap(h<, \alpha, \beta, \mathsf{locals})$ 进行搜索。其中 $h'_<$ 有如下性质:
- 至少包括 $\alpha, \beta$ 中的事务;
- 删除 $\alpha$ 后的 $h'$ 是 $h$ 的一个前缀;
- 如果 $\alpha$ 中的 r 在 $h$ 和 $h'$ 中 read-from 不同的 w,那么 r 应该是整个事务的最后一个事件(为什么?)。
SWAPPING-BASED MODEL CHECKING FOR PREFIX-CLOSED AND CAUSALLY-EXTENSIBLE ISOLATION LEVELS
Extending Histories According to An Oracle Order
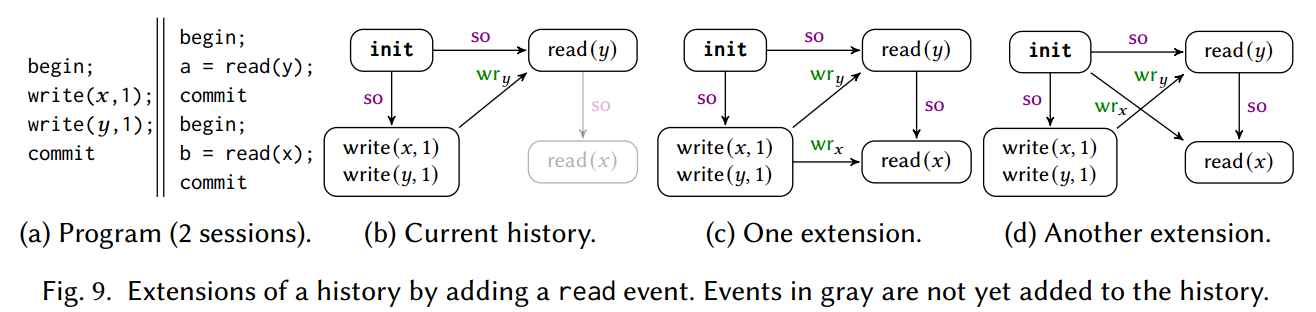
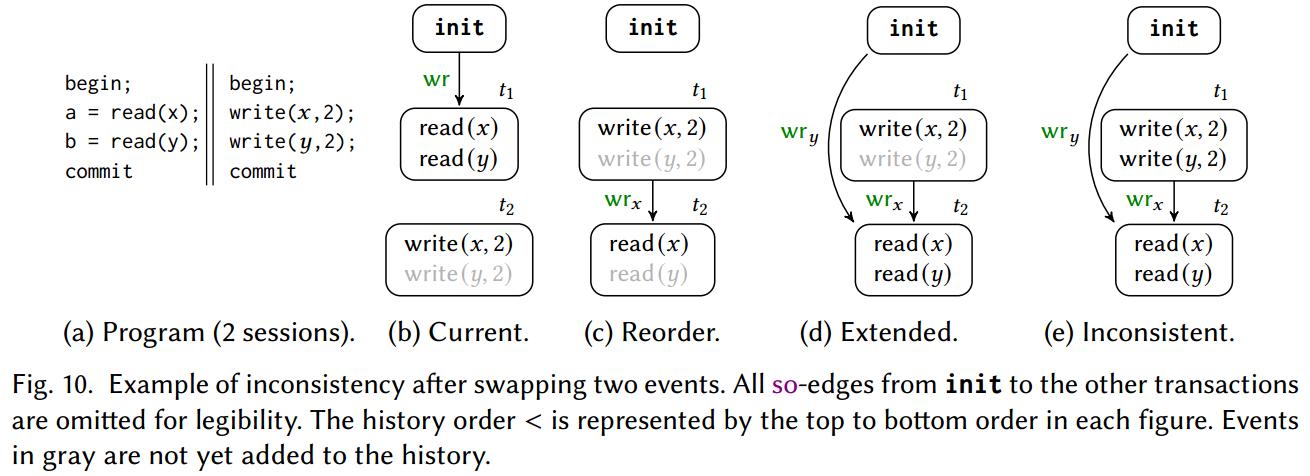
Re-Ordering Events in Histories
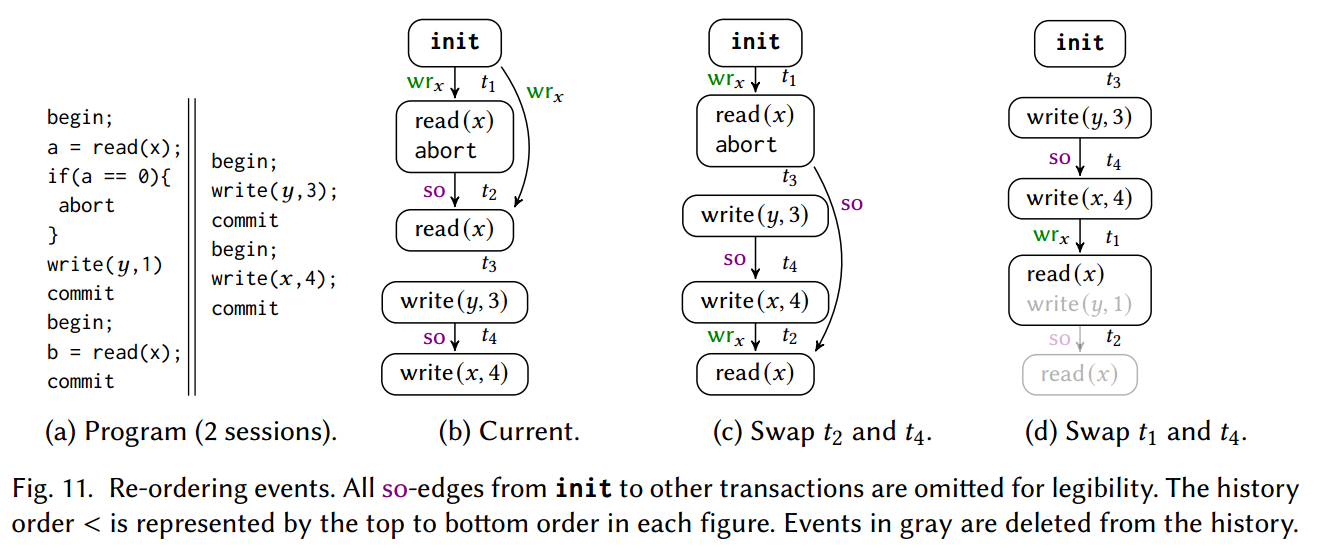
Ensuring Optimality
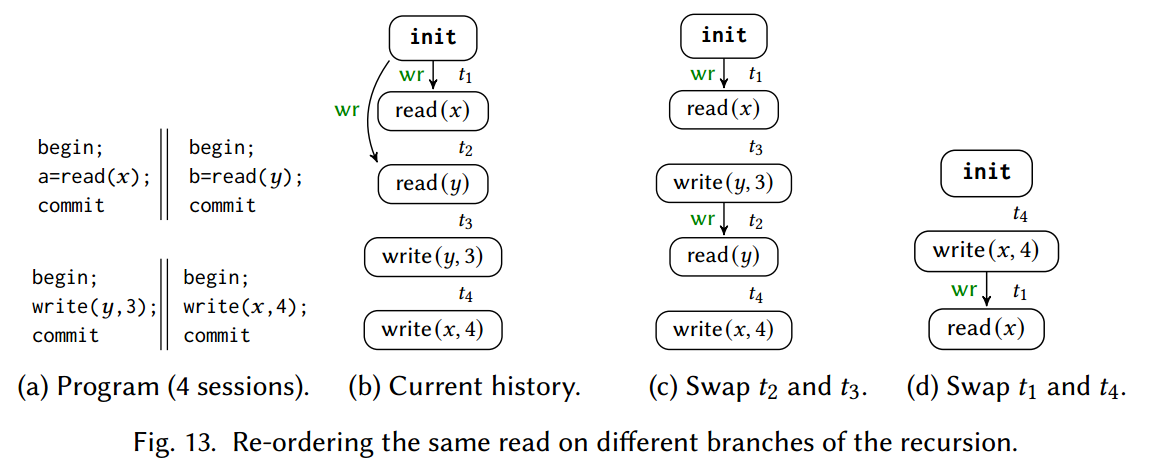
Correctness
SWAPPING-BASED MODEL CHECKING FOR SNAPSHOT ISOLATION AND SERIALIZABILITY
EXPERIMENTAL EVALUATION
Implementation
我们将我们的算法实现为 JPF 中 DFSearch 类的扩展。 出于性能原因,我们实现了这些算法的迭代版本,其中递归调用的输入大致被维护为历史集合,而不是依赖于调用堆栈。 为了检查历史记录与给定隔离级别的一致性,我们实现了 Biswas 和 Enea [2019] 提出的算法。
我们的工具将 Java 程序作为输入,并将隔离级别作为参数。 我们假设程序使用固定的 API 与数据库交互,类似于键值存储接口。 该 API 包含用于启动/结束事务以及读取/写入全局变量的特定方法。 需要固定的 API 来独立于 JVM 状态(Java 程序的状态)来维护数据库状态并更新每次数据库访问中的当前历史记录。 这依赖于一种将从数据库状态读取的值“传输”到 JVM 状态的机制。
Benchmark
Experimental Results
RELATED WORK
Checking Correctness of Database-Backed Applications
其中一条工作路径涉及隔离级别的逻辑形式化 [Adya et al. 2000; Berenson et al. 1995; Biswas and Enea 2019; Cerone et al. 2015; X3 1992]。我们的工作依赖于 Biswas 和 Enea [2019] 引入的隔离级别的公理定义,这些定义还研究了检查给定历史是否满足某个隔离级别的问题。我们的 SMC 算法依靠这些算法来检查历史记录与给定隔离级别的一致性。
另一条工作路径重点是发现“异常”的问题:在可序列化下不可能的行为。这通常是通过对应用程序代码进行静态分析来完成的,该分析构建了一个静态依赖关系图,该图过度近似了应用程序所有可能执行中的数据依赖关系 [Bernardi and Gotsman 2016; Cerone and Gotsman 2018; Fekete et al. 2005; Gan et al. 2020; Jorwekar et al. 2007; Warszawski and Bailis 2017]。给定隔离级别的异常对应于该图中的特定类别的循环。静态依赖图在表示可行执行方面非常不精确,从而导致误报。误报的另一个来源是异常可能不是错误,因为应用程序可能已经被设计为处理不可序列化的行为 [Brutschy et al. 2018; Gan et al. 2020]。最近的工作试图通过使用更精确的应用程序逻辑编码 [Brutschy et al 2017, 2018] 或使用用户引导的启发式方法 [Gan et al 2020] 来解决这些问题。另一种方法包括对应用程序逻辑和一阶逻辑中的隔离级别进行建模,并依靠 SMT 求解器来搜索异常 [Kaki et al. 2018; Nagar and Jagannathan 2018; Ozkan 2020],或定义断言检查的专门化简 [Beillahi et al 2019a,b]。我们基于 SMC 的方法不会产生误报,因为我们系统地仅枚举允许检查用户定义断言的程序的有效执行。
一些工作研究了推理弱隔离下执行的应用程序的正确性的问题,并在必要时引入额外的同步 [Balegas et al. 2015; Gotsman et al. 2016; Li et al. 2014; Nair et al. 2020]。这些基于静态分析或逻辑证明论证。修复应用程序的问题与我们的工作正交。
MonkeyDB [Biswas et al 2021] 是一个模拟存储系统,用于测试存储支持的应用程序。虽然能够扩展到更大的代码,但它具有固有的测试不完整性。与 MonkeyDB 不同,我们的算法对执行进行系统且完整的探索,并且至少可以在某些有界上下文中建立正确性,并且它们避免冗余,多次枚举等效执行。此类保证超出了 MonkeyDB 的范围。
Dynamic Partial Order Reduction
Abdulla 等人 [2017b] 引入了源集(source sets)的概念,为 Mazurkiewicz 迹等价提供了第一个强最优 DPOR 算法。其他作品研究了粗略等价关系的 DPOR 技术,例如 [Abdulla et al. 2019; Agarwal et al. 2021; Aronis et al. 2018; Chalupa et al. 2018; Chatterjee et al. 2019]。在所有情况下,当确保强最优性时,空间复杂度是指数级的。
其他工作侧重于通过针对特定内存模型将 DPOR 扩展到弱内存模型 [Abdulla et al 2017a, 2016, 2018; Norris 和 Demsky 2013] 或者通过相对于公理定义的内存模型进行参数化 [Kokologiannakis et al 2022, 2019; Kokologiannakis 和 Vafeiadis 2020]。其中一些作品可以处理更粗略的读取等价性,例如,[Abdulla et al 2018; Kokologiannakis et al. 2022, 2019; Kokologiannakis 和 Vafeiadis 2020]。我们的算法建立在 Kokologiannakis et al. [2022] 的工作基础上,该工作首次提出了一种强最优且多项式空间的 DPOR 算法。数据库隔离级别的定义与弱内存模型有很大不同,这使得这些先前的工作无法以直接方式扩展。这些定义包括事务的语义,事务是读取和写入的集合,这提出了新的困难挑战。例如,关于共享内存的现有 DPOR 算法的完整性和(强)最优性的推理对于调度程序(Next 函数)来说是不可知的,而我们的 explore-ce 算法的强最优性依赖于调度程序最多保持一个事务挂起一次。此外,与 TruSt 不同,explore-ce 确保交换的事件不能再次交换,并且历史顺序 < 是 $\so \cup \wr$ 的扩展。这使得我们的完整性和最优性证明完全不同。此外,即使对于每笔交易一次访问的交易程序,其中 SER 和 SC 是等效的,对于任何 $I_0 \in \set{RC, RA, CC}$,SC 下的 TruSt 和 explore-ce* ($I_0$, SER) 也不一致。在这种情况下,TruSt 仅枚举 SC 一致的历史,但代价是在每一步解决 NP 完全问题,而 explore-ce* 步骤的成本是多项式时间,代价是不是强最优。此外,我们还确定了隔离级别(SI 和 SER),对于这些隔离级别,不可能使用基于交换的算法来确保强最优性和多项式空间边界,这种问题在之前的工作中尚未研究过。
CONCLUSIONS
[^Biswas]: Ranadeep Biswas and Constantin Enea. 2019. On the complexity of checking transactional consistency. Proc. ACM Program. Lang. 3, OOPSLA (2019), 165:1–165:28. https://doi.org/10.1145/3360591

