EagleBear2002 的博客

这里必须根绝一切犹豫，这里任何怯懦都无济于事

高级算法-复习

发表于 更新于 分类于 ，
本文字数： 9.1k 阅读时长 ≈ 8 分钟

摘要

本文整理了 2025Spring 李言辉老师的《高级算法》课程复习题。

部分内容来自《算法导论》，推荐作为复习参考。

算法复杂度

  • 最坏复杂度：算法在任何输入实例上运行时间的最坏情况，记为 $T_{\text{worst}}(n)$。
  • 举例：快速排序最坏情况 $O(n^2)$（当数组已有序且主元选择不当）。
  • 平均复杂度：算法在所有可能输入实例上运行时间的期望，记为 $T_{\text{avg}}(n)$。
  • 举例：快速排序平均情况 $O(n \log n)$。
  • 最优复杂度：算法在“最优”输入实例上的最低运行时间（较少使用）。
  • 举例：冒泡排序在已有序数组上为 $O(n)$。

渐近记号定义与函数证明

定义：

$$ O(g(n)) = \set{ f(n) \mid \exists c>0, n_0>0 : 0 \leq f(n) \leq cg(n), \ \forall n \geq n_0 } $$

$$ \Omega(g(n)) = \set{ f(n) \mid \exists c>0, n_0>0 : 0 \leq cg(n) \leq f(n), \ \forall n \geq n_0 } $$

$$ \Theta(g(n)) = O(g(n)) \cap \Omega(g(n)) $$

《算法导论》给出了三者的形象描述：

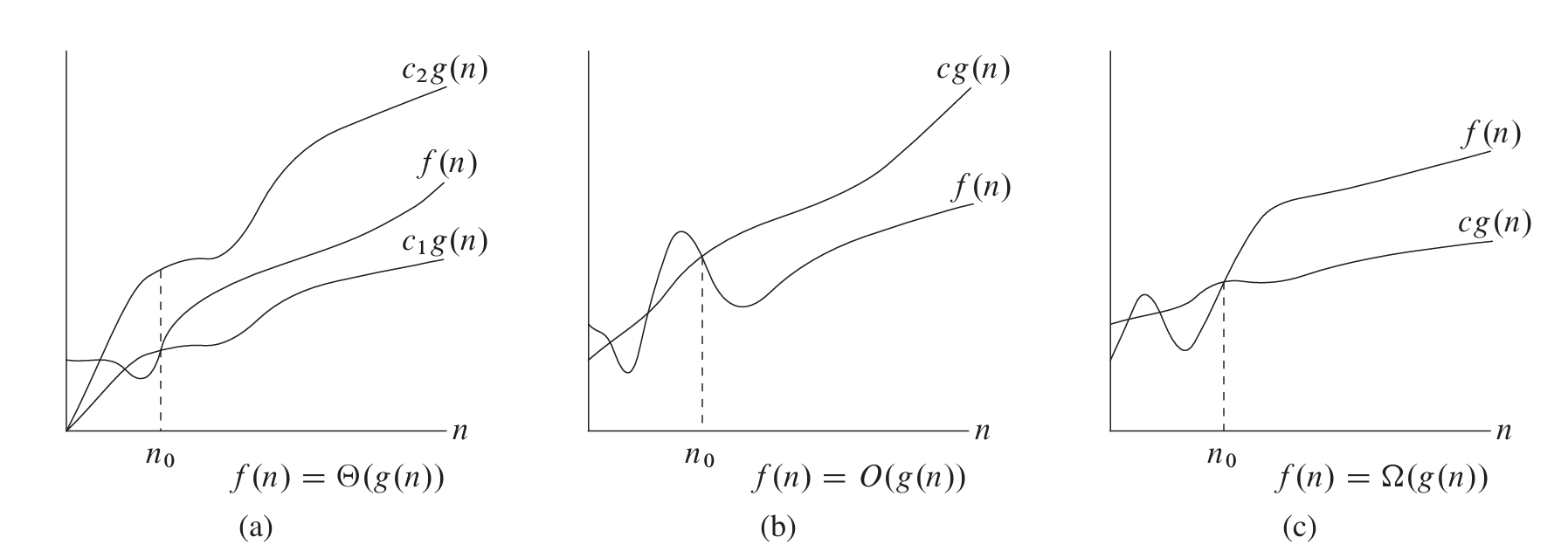
函数证明：

$$ 3n^3 + 2n^2 + 10 \in \Theta(n^3) $$

证明：

$$ \begin{align} \text{上界：} & 3n^3 + 2n^2 + 10 \leq 3n^3 + 2n^3 + 10n^3 = 15n^3, \ \forall n \geq 1 \ & \Rightarrow 3n^3 + 2n^2 + 10 \in O(n^3) \ \text{下界：} & 3n^3 + 2n^2 + 10 \geq 3n^3, \ \forall n \geq 0 \ & \Rightarrow 3n^3 + 2n^2 + 10 \in \Omega(n^3) \end{align}

\therefore 3n^3 + 2n^2 + 10 \in \Theta(n^3) $$

递归关系求解

解递归式：

$$ a_n = r_1 a_{n-1} + r_2 a_{n-2} $$

解法（特征方程法）：

  1. 特征方程： $x^2 - r_1 x - r_2 = 0$，解得根 $x_1, x_2$。
  2. 通解： $$ a_n = \begin{cases} c_1 x_1^n + c_2 x_2^n & (x_1 \neq x_2) \ (c_1 + c_2 n) x_1^n & (x_1 = x_2) \end{cases} $$
  3. 代入初始条件求解 $c_1, c_2$。

例如，对于

$$ a_0 = 1, a_1 = 1, a_n = a_{n-1} + a_{n-2}, $$

则特征方程为

$$ x^2 - x - 1 = 0 $$

其解为

$$ x_1 = \frac{1 - \sqrt{5}}{2}, x_2 = \frac{1 + \sqrt{5}}{2} $$

对于通项公式

$$ a_n = c_1 x_1^n + c_2 x_2^n $$

代入

$$ a_0 = 1, a_1 = 1 $$

解得

$$ c_1 = \frac{5 - \sqrt{5}}{10}, c_2 = \frac{5 + \sqrt{5}}{10} $$

则通项公式为

$$ a_n = \frac{5 - \sqrt{5}}{10} (\frac{1 - \sqrt{5}}{2})^n + \frac{5 + \sqrt{5}}{10} (\frac{1 + \sqrt{5}}{2})^n $$

主定理应用

求解一般式：

$$ T(n) = bT(n/c) + f(n) $$

主定理：

  • 若 $f(n) \in O(n^{\log_c b - \epsilon})$，则 $T(n) \in \Theta(n^{\log_c b})$。
  • 若 $f(n) \in \Theta(n^{\log_c b} \log^k n)$，则 $T(n) \in \Theta(n^{\log_c b} \log^{k+1} n)$。
  • 若 $f(n) \in \Omega(n^{\log_c b + \epsilon})$ 且 $a f(n/c) \leq k f(n)$（$k<1$），则 $T(n) \in \Theta(f(n))$。

示例 1：$T(n) = 2T(n/2) + n \log n$

$\log_b a = 1$，$f(n)=n\log n=\Theta(n^1 \log^1 n) \Rightarrow T(n)=\Theta(n \log^2 n)$。

示例 2：$T(n) = 3T(n/2) + n \log n$

$$ T(n) \in \Theta(3^{\log_2 n}) = \Theta(n^{\log_2 3}) $$

堆的定义与操作

  • 定义：完全二叉树，满足堆性质（小根堆：$ \forall i,\ A[i] \leq A[\text{child}(i)] $）。
  • 数组表示：下标从 1 开始，$A[i]$ 的父节点在 $A[\lfloor i/2 \rfloor]$，子节点在 $A[2i]$ 和 $A[2i+1]$。
  • 操作：
    • Insert(x)：插至末尾，向上调整（$\textbf{UpHeap}$），时间复杂度 $O(\log n)$。
    • ExtractMin()：取根元素，末尾元素移至根，向下调整（$\textbf{DownHeap}$），时间复杂度 $O(\log n)$。

快排平均复杂度分析复用

解递归式： $A(n) = (n-1) + \frac{2}{n} \sum_{i=1}^{n-1} A(i)$

步骤：

  1. 两边乘 $n$： $nA(n) = n(n-1) + 2 \sum_{i=1}^{n-1} A(i)$。
  2. 写 $(n-1)A(n-1) = (n-1)(n-2) + 2 \sum_{i=1}^{n-2} A(i)$。
  3. 相减消和式： $$ \begin{align*} nA(n) - (n-1)A(n-1) &= 2n-2 + 2A(n-1) \ \Rightarrow A(n) &= A(n-1) \frac{n+1}{n} + \frac{2n-2}{n} \ \Rightarrow \frac{A(n)}{n+1} &= \frac{A(n-1)}{n} + \frac{2(n-1)}{n(n+1)} \end{align*} $$
  4. 令 $B(n) = \frac{A(n)}{n+1}$，则有：

$$ B(n) = B(n-1) + \frac{2(n-1)}{n(n+1)} = B(n-1) + \frac{3}{n+1} - \frac{1}{n} $$

$$ B(n) = B(0) + \sum_{i=1}^{n}(\frac{3}{n+1} - \frac{1}{n}) $$

显然，$B(n) \in O(\log n)$，因此 $A(n) \in O(n \log n)$。

对抗策略分析

含义：通过构造最坏输入序列证明算法复杂度的下界。

问题：在数组中同时找到最大元素和最小元素

算法（分组比较法）：

  • 基本思路：采用分治策略，将元素两两分组处理，减少冗余比较。
  • 具体步骤：
    1. 分组比较：将元素分为 $\lfloor n/2 \rfloor$ 对（若 $n$ 为奇数，则保留一个元素单独处理）。每对比较一次，得到局部最小值和局部最大值（较小者参与最小值后续比较，较大者参与最大值后续比较）。比较次数：$\lfloor n/2 \rfloor$。
    2. 找全局最小值：从所有局部最小值（共 $\lceil n/2 \rceil$ 个）中找全局最小值，比较次数：$\lceil n/2 \rceil - 1$。
    3. 找全局最大值：从所有局部最大值（共 $\lceil n/2 \rceil$ 个）中找全局最大值，比较次数：$\lceil n/2 \rceil - 1$。
  • 总比较次数：
    • $n$ 为偶数：$\frac{n}{2} + 2 \times \left( \frac{n}{2} - 1 \right) = \frac{3n}{2} - 2$。
    • $n$ 为奇数：设 $n = 2k + 1$，比较次数为 $3k - 1 = \left\lceil \frac{3n}{2} \right\rceil - 2$（因为 $\left\lceil \frac{3n}{2} \right\rceil = \frac{3n + 1}{2}$ 当 $n$ 为奇数）。

下界证明：$\left\lceil \frac{3n}{2} \right\rceil - 2$（对抗策略）

  • 目标：证明任何算法在最坏情况下都至少需要 $\left\lceil \frac{3n}{2} \right\rceil - 2$ 次比较。
  • 对抗策略：对手通过控制比较结果最大化算法的不确定性：
    • 初始状态：每个元素同时是最大值和最小值的候选（共 $2n$ 个候选状态）。
    • 当算法比较两个元素 $a$ 和 $b$：
      • 若两者均同时是最大值和最小值候选：对手返回 $a < b$（固定顺序），并更新：
        • $a$ 不再是最大值候选（因为 $\exists b > a$），
        • $b$ 不再是最小值候选（因为 $\exists a < b$）。
        • 效果：最大值候选数减 1，最小值候选数减 1。
      • 其他情况：对手选择结果以最小化状态减少（如仅使一个候选集减 1）。
  • 候选状态变化：
    • 最大值候选数需从 $n$ 减至 $1$（减少 $n-1$ 个），
    • 最小值候选数需从 $n$ 减至 $1$（减少 $n-1$ 个）。
    • 总需减少状态数：$2(n-1)$。
  • 关键观察：
    • 最有效的比较（同时减少两个候选集）最多发生 $\lfloor n/2 \rfloor$ 次（即分组阶段），对应减少 $2 \lfloor n/2 \rfloor$ 个状态。
    • 剩余状态数：$2(n-1) - 2 \lfloor n/2 \rfloor$。
    • 剩余比较需单步减少（每次减 1），所需比较次数：$2(n-1) - 2 \lfloor n/2 \rfloor$。
  • 总最坏比较次数： $$ \underbrace{\left\lfloor \frac{n}{2} \right\rfloor}{\text{分组}}+\underbrace{2(n-1) - 2 \left\lfloor \frac{n}{2} \right\rfloor}{\text{剩余}} = 2n - 2 - \left\lfloor \frac{n}{2} \right\rfloor $$ 结合奇偶性分析：
    • 若 $n$ 为偶数：$2n - 2 - n/2 = 3n/2 - 2$。
    • 若 $n$ 为奇数：$2n - 2 - (n-1)/2 = (4n - 4 - n + 1)/2 = (3n - 3)/2 = \frac{3n}{2} - \frac{3}{2}$，而 $\left\lceil \frac{3n}{2} \right\rceil - 2 = \frac{3n + 1}{2} - 2 = \frac{3n - 3}{2}$（因为 $\lceil 3n/2 \rceil = (3n+1)/2$），故相等。
  • 紧致性：分组比较法达到此下界，证明其最优。

问题：在 $n$ 个元素中找第二大元素

算法（锦标赛方法）

  • 基本思路：模拟单淘汰锦标赛：
    1. 阶段 1（找最大值）：元素两两比较，胜者（较大者）晋级。重复直至确定最大值（冠军）。
      • 比较次数：$n-1$（每场淘汰 1 个元素）。
      • 最大元素的直接对手：在晋级路径中，最大值依次击败 $k$ 个元素，其中 $k = \lceil \log n \rceil$（树的高度）。
    2. 阶段 2（找第二大）：在最大元素的 $k$ 个直接对手中，用 $k-1$ 次比较找到最大值（即第二大）。
  • 总比较次数：$(n-1) + (\lceil \log n \rceil - 1) = n + \lceil \log n \rceil - 2$。

下界证明：$n + \lceil \log n \rceil - 2$（对抗策略）

  • 核心定理：第二大元素 $S$ 必须直接与最大元素 $M$ 比较过（否则无法验证其为第二大）。

反证：若 $S$ 未与 $M$ 比较，则存在元素 $T$ 使得 $M > T > S$ 且算法未比较 $T$ 与 $S$（对手可设置 $T$ 破坏 $S$ 的第二大地位）。

  • 对抗策略：
    • 对手维护最大元素候选集和第二大元素候选集。
    • 当算法比较两个元素时，对手选择结果使：
      • 最大元素 $M$ 尽可能迟地被确定（需至少 $n-1$ 次比较），
      • 第二大元素候选集尽可能大（至少保留 $\lceil \log n \rceil$ 个候选）。
  • 下界分析：
    1. 确认最大元素 $M$：需至少 $n-1$ 次比较（$M$ 必须击败所有其他元素）。
    2. 确认第二大元素 $S$：$S$ 必须直接败给 $M$，且是 $M$ 的直接对手中的最大者。
      • $M$ 至少有 $\lceil \log n \rceil$ 个直接对手（因为其晋级路径高度为 $\lceil \log n \rceil$）。
      • 在 $\lceil \log n \rceil$ 个候选中找到最大值需 $\lceil \log n \rceil - 1$ 次比较。
  • 总比较次数下界： $$ (n-1) + (\lceil \log n \rceil - 1) = n + \lceil \log n \rceil - 2. $$
  • 紧致性：锦标赛方法达到该下界，证明其最优性。

平摊分析

含义：将操作序列的总代价分摊到每个操作的平均代价。

栈的 MultiPop 操作：平摊分析（会计法）

问题描述

  • 栈支持两种操作：
    • Push(x)：压入元素 $x$，实际代价为 $1$。
    • MultiPop(k)：弹出栈顶 $k$ 个元素（若元素不足，则弹出所有），实际代价为弹出元素个数。
  • 序列从空栈开始，分析 $n$ 次操作的平摊代价。

会计法分析

  • 平摊代价分配：
    • Push：分配平摊代价 $$2$。
      • $$1$ 用于支付 Push 操作本身的实际代价。
      • $$1$ 存储为信用，用于支付该元素未来被弹出的代价。
    • MultiPop(k)：分配平摊代价 $$0$。
      • 弹出每个元素时，使用其存储的 $$1$ 信用支付实际代价。
  • 总平摊代价分析：
    • 设操作序列中有 $t$ 次 Push 操作。
    • Push 总平摊代价：$2t$。
    • MultiPop 平摊代价：$0$。
    • 总平摊代价 $=2t$。
  • 实际代价说明：
    • MultiPop 弹出的元素总数 $\leq t$（因元素均由 Push 压入）。
    • 总实际代价 $\leq$（Push 代价）$+$（MultiPop 弹出总代价）$= t + t = 2t$。
  • 平摊结论：
    • 总实际代价 $\leq 2t \leq 2n$（$n$ 为操作序列长度）。
    • 每个操作的平均代价 $O(1)$。

删除大于中位数的元素：DeleteLargerHalf（平摊分析：势能法）

问题描述

  • 动态集合支持：
    • Insert(x)：插入元素 $x$，实际代价 $O(1)$。
    • DeleteLargerHalf()：删除大于中位数的元素（即删除 $\lceil n/2 \rceil$ 个最大元素），实际代价 $O(n)$（使用线性时间选择算法）。
  • 分析 $m$ 次操作序列的平摊代价。

势能法分析

  • 势能函数：$\Phi = 2 \cdot |S|$，其中 $|S|$ 是集合当前元素个数。
  • 操作分析：
    • Insert 操作：
      • 实际代价：$1$。
      • 势能变化：$\Delta\Phi = 2(|S|+1) - 2|S| = 2$。
      • 平摊代价：$1 + 2 = 3$。
    • DeleteLargerHalf 操作：
      • 设操作前集合大小为 $n$。
      • 实际代价：$c \cdot n$（$c$ 为正常数，来自选择算法）。
      • 删除元素数：$d = \lceil n/2 \rceil$。
      • 势能变化：$\Delta\Phi = 2(n - d) - 2n = -2d$。
      • 平摊代价：$c \cdot n - 2d$。

平摊代价上界证明

  • 关键不等式： $$ c \cdot n - 2d \leq cn - 2 \cdot \frac{n}{2} = (c-1)n $$ 因为 $d \geq n/2$。
  • 总平摊代价：
    • 设序列中有 $I$ 次 Insert，$D$ 次 DeleteLargerHalf。
    • Insert 总平摊代价：$3I$。
    • DeleteLargerHalf 总平摊代价：$\sum_{i=1}^D (c \cdot n_i - 2d_i)$。
    • 总平摊代价 $\leq 3I + (c-1) \sum_{i=1}^D n_i$。

$\sum n_i$ 的界

  • 引理：$\sum_{\text{del}} n_i \leq 2I$。
    • 证明：
      • 记 $d_i$ 为第 $i$ 次删除的元素数，则 $\sum_{i=1}^D d_i = I - L \leq I$（$L$ 为最终元素数）。
      • 由 $d_i \geq n_i / 2$，得 $n_i \leq 2d_i$，求和得 $\sum n_i \leq 2\sum d_i \leq 2I$。
  • 总平摊代价： $$ \begin{align*} \text{总平摊} &\leq 3I + (c-1) \cdot 2I \ &= (2c + 1)I \ &= O(I) \end{align*} $$
  • 最终结论：
    • $I \leq m$（$m$ 为操作序列长度）。
    • 总平摊代价 $= O(m)$。
    • 每个操作平摊代价 $O(1)$。

两种分析的核心思想对比

方法 适用场景 核心技巧 分析目标
会计法 操作间存在"预支付"关系 为高风险操作分配额外信用 单次操作平摊代价
势能法 状态变化连续的复杂操作序列 定义势能函数描述系统状态，关联实际代价变化 证明总代价上界

两种方法均证明：单次最坏操作代价虽高，但序列平均代价为常数。

图搜索算法应用

深度优先搜索（DFS）思想：递归探索未访问邻居，回溯时处理节点

应用：

  • 拓扑排序：在 DAG 上运行 DFS，按结束时间逆序排列。
  • 强连通分量（SCC）：Kosaraju 算法（正图 DFS + 反图 DFS）。

广度优先搜索（BFS）思想：按层遍历，使用队列管理节点

应用：

  • 最短路径（无权图）：记录起点到各点的层数（距离）。
  • 任务调度关键路径：基于拓扑序的 BFS 计算最早开始时间。

贪心法原理与应用

  • 思想：局部最优选择扩展至全局解。

  • 特点：高效但不一定全局最优，需证明正确性（贪心选择性质与最优子结构）。

  • 换硬币问题（特定面额）：

    • 策略：每次选最大面额硬币。
    • 证明：若面额满足 $c_i > c_j \Rightarrow c_i \geq 2c_j$，则贪心法最优。

  • 活动安排问题：

    • 策略：选结束时间最早且与已选活动兼容的活动。
    • 证明（贪心选择性）：设最优解包含活动 $a_k$（最早结束），用 $a_k$ 替换另一相容活动结果不变。

动态规划原理与应用

  • 思想：将问题分解为重叠子问题，自底向上或备忘录求解。
  • 特点：需满足最优子结构（子问题最优解组合为原问题最优解）。

最长公共子序列（LCS）

递归式：

$$ \text{LCS}(X_i, Y_j) = \begin{cases} 0 & i=0 \text{ 或 } j=0 \ \text{LCS}(X_{i-1}, Y_{j-1}) + 1 & x_i = y_j \ \max \left{ \text{LCS}(X_{i-1}, Y_j), \text{LCS}(X_i, Y_{j-1}) \right} & x_i \neq y_j \end{cases} $$

伪代码：

1
2
3
4
5
for i from 0 to m:
    for j from 0 to n:
        if i==0 or j==0: dp[i][j] = 0
        elif X[i-1] == Y[j-1]: dp[i][j] = dp[i-1][j-1] + 1
        else: dp[i][j] = max(dp[i-1][j], dp[i][j-1])

最优二叉搜索树（OBST）

关于问题和算法的讲解：最优二叉搜索树 动态规划算法_哔哩哔哩_bilibili

问题定义

  • 二叉搜索树(BST)：满足每个节点的左子树键值 ≤ 该节点键值 ≤ 右子树键值的二叉树
  • 访问频率：每个键 $k_i$ 有搜索频率 $p_i$（成功），区间 $d_i$ 有搜索频率 $q_i$（失败）
  • 目标：构建 BST 使搜索期望代价最小（考虑键值比较次数）
搜索代价公式

$$ E[\text{cost}] = \sum_{i=1}^{n} (\text{depth}(k_i)+1)·p_i + \sum_{i=0}^{n} (\text{depth}(d_i)+1)·q_i $$

核心递归式

令 $e[i][j]$ 表示包含键 $k_i$ 到 $k_j$ 的最优二叉搜索树的期望搜索代价

$$ \boxed{ e[i][j] = \begin{cases} q_{i-1} & \text{if } j = i-1 \ \min\limits_{i \leq r \leq j} \left{ e[i][r-1] + e[r+1][j] + w(i,j) \right} & \text{if } i \leq j \end{cases} } $$

其中：

  • $w(i,j) = \sum_{l=i}^{j} p_l + \sum_{l=i-1}^{j} q_l$（区间总频率）
  • $r$ 为当前子树的根节点

动态规划解法

1. 计算频率前缀和
1
2
3
4
5
# 假设 p[1..n] 和 q[0..n] 已知
w = [[0]*(n+1) for _ in range(n+2)]
for i in range(1, n+1):
    for j in range(i, n+1):
        w[i][j] = w[i][j-1] + p[j] + q[j]
2. 自底向上填表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
e = [[0]*(n+1) for _ in range(n+2)]  # 期望代价
root = [[0]*(n+1) for _ in range(n+1)] # 根选择

# 初始化
for i in range(1, n+2):
    e[i][i-1] = q[i-1]

# 按长度递增填表
for L in range(1, n+1):  # L: 键的个数
    for i in range(1, n-L+2):
        j = i+L-1
        e[i][j] = float('inf')
        for r in range(i, j+1):
            t = e[i][r-1] + e[r+1][j] + w[i][j]
            if t < e[i][j]:
                e[i][j] = t
                root[i][j] = r
示例 ($n=4$)
键 频率 $p_i$ 区间 频率 $q_i$
$k_1$ 0.15 $d_0$ 0.05
$k_2$ 0.10 $d_1$ 0.10
$k_3$ 0.05 $d_2$ 0.05
$k_4$ 0.10 $d_3$ 0.05
$d_4$ 0.10

计算 $e$ 表：

1
2
3
4
5
6
7
j\i |  1       2       3       4
-------------------------------
0   | 0.05
1   | 0.30    0.10
2   | 0.45    0.25    0.05
3   | 0.55    0.35    0.15    0.05
4   | 0.70    0.50    0.30    0.20

最终代价：$e[1][4]=1.75$

时间复杂度分析

  • 三重循环：$O(n^3)$
  • 空间复杂度：$O(n^2)$
  • 重建最优树：根据 root 表递归构造

Knuth 优化

发现最优根位置满足：

$$ \text{root}[i][j-1] \leq \text{root}[i][j] \leq \text{root}[i+1][j] $$

优化后时间复杂度降为 $O(n^2)$：

1
2
3
4
5
6
7
for L in range(1, n+1):
    for i in range(1, n-L+2):
        j = i+L-1
        low = root[i][j-1] if L>1 else i
        high = root[i+1][j] if L>1 else j
        for r in range(low, high+1):  # 优化搜索范围
            ...

OBST vs Huffman 树

特性 最优二叉搜索树 Huffman 编码树
键位置 有序 无序
结构要求 满足 BST 性质 无结构限制
频率类型 成功+失败频率 仅叶节点频率
时间复杂度 $O(n^3)$ 或 $O(n^2)$ $O(n\log n)$
主要用途 搜索优化 数据压缩

OBST 的核心思想：通过动态规划平衡高频键靠近树根，最小化整体期望搜索路径。它在数据库索引、语言模型等需要高效搜索的场景中有重要应用。