\[ \def\po{\mathsf{\textcolor{red}{po}}} \def\so{\mathsf{\textcolor{purple}{so}}} \def\wr{\mathsf{\textcolor{teal}{wr}}} \def\ww{\mathsf{\textcolor{red}{ww}}} \def\rw{\mathsf{\textcolor{blue}{rw}}} \def\vis{\mathsf{\textcolor{orange}{vis}}} \def\arb{\mathsf{\textcolor{pink}{arb}}} \def\Write{\mathsf{Write}} \def\Read{\mathsf{Read}} \def\View{\mathsf{View}} \def\RelWrites{RelWrites} \def\MaxRelWrites{MaxRelWrites} \def\EffWrite{EffWrite} \def\wk{\mathsf{wk}} \def\st{\mathsf{st}} \def\total{\mathsf{total}} \def\read{read} \def\write{write} \def\thru{thru} \def\back{back} \def\ANY{\mathtt{ANY}} \def\ONE{\mathtt{ONE}} \def\QUORUM{\mathtt{QUORUM}} \def\ALL{\mathtt{ALL}} \def\O{\mathcal{O}} \def\RelTerms{RelTerms} \def\VisBasic{VisBasic} \]
摘要
分布式数据存储的开发人员必须牺牲一致性来换取性能和可用性。此类系统实际上可能实现弱一致性模型，例如因果一致性或最终一致性，这对应于不同的成本和对客户端的保证。我们考虑分布式系统的情况，它不仅为客户端提供单一级别的一致性，而且提供多种级别的一致性。这对应于许多实际情况。例如，流行的数据存储（如 Amazon DynamoDB 和 Apache 的 Cassandra）允许应用程序在同一会话中使用单独的一致性级别标记每个查询。在本文中，我们为多级一致性规范提供了一个正式框架，并解决了检查计算是否符合此类规范的问题。我们为这个问题提供了一种原则性的算法方法，并将其应用于具有多级一致性的模型的几个实例。
作者：
Ahmed Bouajjani1, Constantin Enea1, Madhavan Mukund2,3, Gautham Shenoy R.2, and S. P. Suresh 2,3
1Universit´e Paris Diderot, Paris, France {abou,cenea}@irif.fr
2Chennai Mathematical Institute, Chennai, India {madhavan,gautshen,spsuresh}@cmi.ac.in
3CNRS UMI 2000 ReLaX, Chennai, India
Introduction
为了实现可用性和可扩展性，现代数据存储（键值存储）依赖于乐观复制，允许多个客户端对多个副本上的共享数据发出操作，这些副本使用消息传递相互传达更改。这种架构的一个好处是，即使网络连接失败，副本仍可在本地供客户端使用。不幸的是，著名的 CAP 定理 [15] 表明，这种高可用性和对网络分区的容忍度与强一致性不相容，即单个集中式副本处理所有操作的假象。因此，现代复制数据存储通常提供较弱的一致性形式，例如最终一致性 [23] 或因果一致性 [19]，这些一致性最近才被形式化 [6,7,10,22]。
在弱一致性数据存储上编写应用程序非常困难。为了保持正确性，某种形式的同步通常是不可避免的。因此，流行的数据存储（如 Amazon DynamoDB 和 Apache 的 Cassandra）提供了不同级别的一致性，从较弱的形式到强一致性。应用程序可以根据其需求为数据存储中的查询添加合适的一致性级别标签。
大规模数据存储的实现很难构建和测试。例如，它们必须考虑部分故障，即某些组件或网络可能出现故障并产生不完整的结果。确保容错依赖于难以设计和推理的复杂协议。黑盒测试框架 Jepsen1 在许多生产分布式数据存储中发现了大量微妙的问题。
测试数据存储会引发两个问题：(1) 得出一组合适的测试场景，例如要注入系统的故障和要执行的操作集；(2) 有效的算法来检查给定的执行是否满足所考虑的一致性模型。Jepsen 框架表明，第一个问题可以通过随机化来解决，例如随机引入故障并随机选择操作。该解决方案的有效性已在最近的工作中得到正式证明 [21]。第二个问题依赖于一致性模型的适当形式化。
在这项工作中，我们考虑指定提供多级一致性的数据存储的问题，并推导出算法来检查给定的执行是否遵守这种多级一致性规范。
我们以 [10] 中的规范框架为基础，该框架使用两个辅助关系形式化一致性模型：(i) 可见性关系，指定每个操作观察到的操作集；(ii) 仲裁顺序，指定所有副本查看并发操作的顺序。如果存在遵循相关约束集的可见性关系和仲裁顺序，则称执行满足一致性标准。对于提供多级一致性的数据存储的情况，我们考虑多个可见性关系和仲裁顺序，每个一致性级别一个。然后，我们考虑一组公式，这些公式单独指定每个一致性级别，以及不同一致性级别的可见性关系和仲裁顺序如何关联。
基于这种形式化，我们研究了检查给定执行是否满足某个多级一致性规范的问题。一般来说，这个问题是 NP-COMPLETE [6]。但是，我们表明，对于每个值最多写入一次键的执行，对于许多实际有趣的多级一致性规范，这个问题是多项式时间。由于实际的数据存储实现与数据无关 [24]，即它们的行为不依赖于事务中读取或写入的具体值，因此只需考虑每个值最多写入一次的执行即可。这个复杂性结果使用了 [6] 中针对因果一致性情况引入的不良模式的概念。直观地说，不良模式是一组以特定顺序发生的与一致性违规相对应的操作。在本文中，我们提供了一种系统的方法来推导不良模式，这些模式表征了广泛的一致性模型及其组合。
我们的贡献形成了一个有效的算法框架，用于验证提供多级一致性的现代数据存储。据我们所知，我们是第一个研究如此广泛的一致性模型及其组合的渐近复杂性的人，尽管它们在实践中很普遍。
本文的结构如下。我们从一些多级一致性的实际例子开始。在第 3 节中，我们提出了一个用于指定和推理多级一致性的形式化模型。第 4 节描述了用于验证多级一致性的算法。最后我们讨论了相关工作。详细证明可以在技术报告 [8] 中找到。
Multilevel Consistency in the Wild
在本节中，我们将介绍一些现实世界中的多级一致性实例。我们将注意力集中在分布式读写键值数据存储（以下称为读写存储），它由通过键或变量寻址的唯一内存位置组成。在这项工作中，我们交替使用键和变量。这些内存位置的内容来自一个称为值的域。
读写数据存储提供了两个 API 来访问和修改特定内存位置的内容。读取特定内存位置内容的 API 通常名为 Read 或 Get，将值存储到特定内存位置的 API 通常名为 Write 或 Put。在本文中，我们分别将这两种方法称为 Read 和 Write。Read 方法不会更新数据存储的状态，只会向调用该方法的应用程序会话显示部分状态。另一方面，Write 方法会修改数据存储的状态。
通常，应用程序读取数据存储的位置，执行一些本地计算，然后将值写回数据存储。应用程序执行的一系列相关读写操作称为会话。
应用程序期望数据存储能够提供某种一致性保证，即它们从数据存储中读取的数据值是新鲜还是陈旧。它们还寻求与呈现给它们的结果的单调性有关的一些保证。数据存储向应用程序提供的这些保证称为一致性标准。一些流行的一致性标准包括：
- Read-Your-Writes：会话中先前操作的效果将对同一会话中的后续操作可见。
- Monotonic Reads：一旦操作的效果在会话中可见，它将对该会话中的所有后续操作保持可见。
- Monotonic Writes：如果远程操作的效果在会话中可见，则远程操作会话中所有先前操作的效果也可见。
- Causal Consistency：会话中先前操作的效果始终对后续操作可见。此外，如果操作的效果对另一个操作可见，则每个看到后者效果的操作都会看到前者的效果。
- Sequential Consistency：操作的效果可以通过通过在各个会话中交错执行的读取和写入获得的单个顺序执行来解释。
目前，大多数关于测试读写存储行为的文献都侧重于测试特定一致性标准的正确性 [6,7,14]。然而，有些情况下，DynamoDB 和 Cassandra 等数据存储系统为应用程序提供了指定每个读取操作的一致性级别的选择 [11]。有些分布式数据存储库允许一致性配给 [18]，还允许对读取操作提供增量一致性保证 [17]。在每种情况下，我们都需要根据多个一致性标准推断数据存储行为的正确性。
现在我们来看看现实世界中多级一致性的一些例子。在这项工作中，我们假设读取和写入 API 如下。
定义 1（读取和写入 API）
令 \(x\) 为键/变量，\(val\) 表示从数据存储读取/写入的数据，\(level\) 表示一致性级别。
- \(\Write(x, val)\) ：使用值 \(val\) 更新键/变量 \(x\) 所寻址的内存位置的内容。
- \(\Read(x, val, level)\) ：键为 \(x\) 的内存位置的内容相对于一致性级别 \(level\) 为 \(val\)，，其中 \(level \in \set{\ANY, \ONE, \QUORUM, \ALL}\)。
Read-Write Stores with Strong and Weak Reads
以数据存储 Cassandra 为例，它允许应用程序更细粒度地选择一致性级别，例如 \(\set{\ANY, \ONE, \QUORUM, \ALL}\)。它通过确保当使用 ANY 执行读取时，通过查询数据存储的任何可用副本来提供返回值来实现这一点。同样，如果使用 ONE 提交读取操作，则通过查询已知包含该键的至少一个值的副本来提供返回值。另一方面，如果使用 QUORUM 执行读取，数据存储会在查询大多数副本后返回该值。最后，如果使用 ALL 执行读取，则在返回响应之前会查询所有副本。显然，ANY 是最弱的一致性标准，而 ALL 是最强的一致性标准。通常，数据存储通过查询所需的副本子集来回答查询，从而提供与不同一致性标准相关的响应。
通常，在更强的一致性标准下执行的读取操作将花费更多时间，因为它可能必须等待所有待处理操作变为可见，或者在返回结果之前运行共识协议。在某些情况下，应用程序可能会对返回值符合某些较弱一致性标准的读取操作感到满意。考虑一个显示电影院可用座位的 Web 应用程序。应用程序可以选择根据较弱的一致性标准读取可用座位，因为：
- 尝试预订座位的用户数量通常多于可用座位数。等待达成共识或法定人数会减慢每个人的读取速度。因此，更快的响应是可取的。
- 用户看到可用座位的时间与用户决定预订特定座位的时间之间存在滞后。由于同时进行的预订，因此在用户预订座位时，显示的数据可能会过时。
- 用户可能会在最终确定一组座位并为其付款之前改变主意。
因此，Web 应用程序可以选择满足较弱一致性标准的读取，同时允许用户选择座位，然后仅当用户付费时才执行满足更强一致性标准的读取。
考虑图 1 中的示例，其中所有写入请求都在同一副本上处理。对于每个会话，都有一个（可能不同的）指定副本，从该副本返回对弱读取的响应。
在此场景中，强读（对应于一致性级别 ALL）满足顺序一致性，而弱读遵循单调读一致性。因此，由所有写入和弱读组成的片段应该在单调读方面是正确的。同样，由所有写入和强读组成的片段应该在顺序一致性方面是正确的。
图 2(a) 中可以看到与图 1 中的示例相对应的弱片段。此片段对于单调读取是正确的；一旦写入 G 在会话 1 中对读取 C 可见，它就会在整个会话中保持可见。写入 I 对任何其他会话尚不可见。
强片段如图 2(b) 所示。这在顺序一致性方面是正确的，其中通过共识获得的操作顺序为 \(A \to B \to G \to H \to I \to D \to E\)。
但是，由于强读对应于级别 ALL，其中所有副本都已看到先前的写入并已就并发写入的顺序达成一致，因此在强读之后的弱读必须考虑先前强读所看到的影响。因此，数据存储施加了额外的约束。一旦写入对会话中的强读可见，则该写入对该会话中所有后续弱读也可见。这可确保较弱的读取确实会合并会话所看到的先前结果。类似地，对弱读可见的写入是从参与级别 ALL 对应的后续强读的副本进行的。因此，会话中先前弱读可见的影响对后续强读也可见。
有了这些额外的限制，我们就无法再解释读取操作 F，因为写入 G 和 I 的影响在读取 F 时都是可见的。强一致性标准已经保证写入 I 发生在写入 G 之后，从而有效地用值 6 覆盖了值 4。因此，这种行为在多级设置中是不正确的。
现在考虑 Cassandra 的行为，其中写入在其中一个副本（对应于级别 ONE）上执行，弱读取在其中一个副本（对应于级别 ONE）上执行，强读取在副本仲裁（对应于级别 QUORUM）上执行。在这种情况下，先前较弱读取可见的写入效果不一定在后续较强读取中可见，因为执行较弱读取的副本可能不在执行较强读取的副本仲裁中。类似地，会话中先前较强读取可见的写入效果不一定对会话中后续较弱读取可见，因为仲裁中的写入可能尚未到达执行较弱读取的副本。因此，较强和较弱读取可以彼此独立。
最后考虑一下 Amazon DynamoDB Accelerator (DAX) [1] 的情况，它包含一个位于应用程序和 DynamoDB 后端之间的直写缓存。应用程序执行的每个写入操作都首先提交到 DynamoDB 后端，并在缓存中更新。默认情况下，读取是最终一致的，即从缓存中执行读取。如果缓存中不存在该项目，则从后端数据存储中获取该项目，并在将值返回给应用程序之前用该项目更新缓存。但是，应用程序也可以通过调用 ConsistentRead 来请求强一致性读取。在这种情况下，从后端读取值并返回给应用程序，而不缓存结果。应用程序进行的任何后续最终一致性读取都可能无法反映先前强一致性读取返回的值。在 DAX 的情况下，可以观察到，对弱最终一致性读取可见的写入效果对后续的强一致性读取也可见，因为这些写入也存在于 DynamoDB 后端。但是，对强一致性读取可见的写入效果不一定对后续的弱最终一致性读取可见。
从这些多级一致性的例子中，我们可以看到，另一个一致性标准的存在可以对用于解释历史正确性的可见性和仲裁关系的选择施加额外的约束。在下一节中，我们将提供一个正式框架，用于对具有多个一致性级别的读写数据存储的行为进行建模。
Formalizing Multilevel Consistency
我们扩展了 [9] 中提供的用于建模读写存储行为的正式框架。应用程序提交给数据存储的每个操作都是 Read 或 Write 操作，其签名在定义 1 中给出。
我们用 Vars 表示读写存储中的所有变量集，并假设写入读写存储的每个值都是自然数 \(val \in \mathbb{N}\)。我们假设所有变量最初都是未定义的，其值 \(\bot\)。
为简单起见，我们仅假设两个一致性级别，即弱和强，分别用 \(\wk\) 和 \(\st\) 表示，其中与 \(\wk\) 级别相对应的一致性标准严格弱于与 \(\st\) 级别相对应的一致性标准。一致性标准之间的比较在定义 7 中正式定义。
应用程序观察到的读写数据存储的行为是它在存储上执行的读写序列。相关读写操作的序列称为会话。因此，每个会话看到的读写存储的行为是该会话中执行的读/写操作的全序。
读写存储的行为是所有会话看到的行为的集合。在图 1 中，我们看到了访问数据存储的三个会话观察到的数据存储行为。我们将这种行为称为混合历史，正式定义如下：
定义 2（混合历史）
一个读写存储的混合历史是一个对 \(H = (\O, \so)\)，其中 \(\O\) 是读写操作的集合，而 \(\so\) 是被称为会话顺序的全序集合。
对于历史 \(H\)，我们定义以下 \(\O\) 的子集。
- \(\O_{\Read}\) 是在 \(H\) 中发生的读操作的集合；
- \(\O_{\Write}\) 是在 \(H\) 中发生的写操作的集合；
- \(\O_{\wk} = \O_{\Write} \cup \{\Read(x, val, level) \in \O_{\Read} \mid level = \wk\}\)（在 \(H\) 中发生的弱操作的集合）；
- \(\O_{\st} = \O_{\Write} \cup \{\Read(x, val, level) \in \O_{\Read} \mid level = \st\}\)（在 \(H\) 中发生的强操作的集合）。
\(H\) 的弱片段表示为 \(H_{\wk} = (\O_{\wk}, \so \cap (\O_{\wk} \times \O_{\wk}))\)。类似地，\(H\) 的强片段表示为 \(H_{\st} = (\O_{\st}, \so \cap (\O_{\st} \times \O_{\st}))\)。请注意，我们将写操作视为强和弱片段的一部分。
- 对于 \(X \subseteq \O \times \O\) 和 \(\ell \in \{\Read, \Write, \wk, \st\}\)，\(X \upharpoonright_{\ell} = X \cap (\O_{\ell} \times \O_{\ell})\)；
- 对于 \(X, Y \subseteq \O \times \O\)，\(X;Y = \{(x, y) \mid \exists z : (x, z) \in X \land (z, y) \in Y\}\) 是 \(X\) 和 \(Y\) 的组合；
- 对于 \(X \subseteq \O \times \O\)，\(\total(X)\) 表示 \(X\) 是一个全序。
当读写存储的副本从应用程序接收一个操作时，它决定已知于该副本的旧操作（要么是从应用程序接收的，要么是从数据存储的其他副本接收的）的效果应如何对新操作可见。在历史上的可见性关系指定了对操作可见的操作集。
定义 3（可见性关系）
在历史 \(H = (\mathcal{O}, \so)\) 上的可见性关系 \(\vis\) 是 \(\mathcal{O}\) 上的无环关系。对于 \(o, o' \in \mathcal{O}\)，我们用 \(o \xrightarrow{\vis} o'\) 表示操作 \(o\) 的效果对操作 \(o'\) 可见。
如果一对操作 \(o, o'\) 没有 \(\vis\) 关系，我们称它们为并发操作，表示为 \(o \parallel_{\vis} o'\)。
我们定义操作 \(o\) 关于可见性关系 \(\vis\) 的视图，记作 \(\View_{\vis}(o)\)，是所有对 \(o\) 可见的写操作的集合。
对于图 1 中的历史，我们可以定义一个可见性关系为
\[ \{A \xrightarrow{\vis} B, G \xrightarrow{\vis} C, G \xrightarrow{\vis} D, H \xrightarrow{\vis} D, G \xrightarrow{\vis} E, H \xrightarrow{\vis} E, I \xrightarrow{\vis} E, G \xrightarrow{\vis} F\} \]
当副本相互通信时，它们需要协调并发写操作的效果，以便最终收敛到同一状态。在会聚数据存储的情况下，这是通过使用诸如“最后写入者获胜”这样的规则来完成的，该规则完全排序所有写操作。这被抽象为仲裁关系，它是历史中所有写操作的全序。我们将仲裁关系表示为 \(\arb\)。我们假设仲裁关系与可见性关系一致，这意味着对于一对写操作 \(o\) 和 \(o'\)，如果 \(o\) 对 \(o'\) 可见，则 \(o\) 在 \(\arb\) 中位于 \(o'\) 之前。
定义 4（仲裁关系）
在混合历史 \(H = (\mathcal{O}, \so)\) 上的仲裁关系 \(\arb\) 是 \(\mathcal{O}_{\Write}\) 上的全序。对于 \(o_i, o_j \in \mathcal{O}\)，我们说 \(o_i \xrightarrow{\arb} o_j\) 表示操作 \(o_i\) 在操作 \(o_j\) 之前被排序。
对于图 1 中的历史，仲裁关系可以是全序
\[ A \xrightarrow{\arb} G \xrightarrow{\arb} H \xrightarrow{\arb} I \]
我们用读写存储的功能规范来定义混合历史的正确性。
设 \(H\) 是一个混合历史。设 \(\vis\) 和 \(\arb\) 是在 \(H\) 上的可见性和仲裁关系。
我们说写操作 \(o'\) 是读操作 \(o\) 的相关写操作，当且仅当 \(o'\) 在 \(o\) 的视图中，并且 \(o\) 和 \(o'\) 操作于同一个变量。所有与 \(o\) 相关的写操作的集合，记作 \(\RelWrites_{\vis}(o)\)，被定义为集合 \(\set{o' \in \View_{\vis}(o) \mid o 和 o' 操作同一个变量}\)。
\(\MaxRelWrites_{\vis}(o)\) 是写操作关于 \(\vis\) 的最大元素的集合，被定义为
\[ \MaxRelWrites_{\vis}(o) = \set{o' \in \RelWrites_{\vis}(o) \mid \forall o'' \in \RelWrites_{\vis}(o) : o'' \xrightarrow{\vis} o' \vee o'' \parallel_{\vis} o'} \]
读操作 \(o\) 的有效写操作，记作 \(\EffWrite^{\arb}_{\vis}(o)\)，被定义为根据仲裁关系从 \(o\) 的最大相关写操作集中选择的最大写操作。
\[ \EffWrite^{\arb}_{\vis}(o) = \begin{cases} \max(\arb \upharpoonright_{\MaxRelWrites_{\vis}(o)}) & \text{if } \MaxRelWrites_{\vis}(o) \neq \emptyset \\ \bot & \text{otherwise} \end{cases} \]
定义 5（读写存储的功能正确性）
设 \(H = (\O, \so)\) 是一个具有可见性关系 \(\vis\) 和仲裁关系 \(\arb\) 的读写数据存储的混合历史。我们说 \((H, \vis, \arb)\) 功能上正确，当且仅当对于每个读操作 \(o = \Read(x, val, level)\)，以下条件成立。
- 如果 \(\EffWrite^{\arb}_{\vis}(o) = \bot\)，则 \(val = \bot\)（即，在 \(o\) 发生时没有对 \(x\) 的写操作）。
- 如果 \(o' = \EffWrite^{\arb}_{\vis}(o)\)，则 \(o'\) 写入了值 \(val\)，即 \(o\) 读到了“最近的”写操作。
接下来，我们正式地通过一组公式定义一致性标准。我们的定义改编自 [13] 中约束的定义。
定义 6（一致性标准）
关系项 \(\tau\) 是由形式 \(r_1; \cdots ; r_k\) （\(k \geq 1\)）组成的组合，其中每个 \(r_i \in \set{so, vis}\)。一致性标准是集合 \(\set{\tau \subseteq vis \mid \tau 是关系项} \cup \set{\total(vis)}\) 的子集。
因此，一致性标准是一个可能为空的可见性约束集合和一个可选的全序约束。为了简化表示，我们通常将约束写成合取式。
请注意，\(so\) 和 \(vis\) 是变量，通常解释为历史中的 \(\so\) 和 \(\vis\) 关系的限制。如下面所示，我们总是需要一个额外的约束，即 \(\vis \upharpoonright_{\Write} \subseteq \arb\)（因此它没有明确包含在一致性标准中）。
TODO：定义中的 \(so, vis\) 和 \(\so, \vis\) 到底是什么关系？
对于一致性标准 \(\alpha\)，\(\RelTerms(\alpha)\) 是在 \(\alpha\) 中出现的所有关系项的集合，而 \(\VisBasic(\alpha)\) 是 \(\alpha\) 中所有可见性约束的集合，不包括全序约束 \(\total(\vis)\)。
定义 7（历史中的一致性标准）
设 \(H = (\O, \so)\) 是一个混合历史，设 \(\vis\) 和 \(\arb\) 是在 \(H\) 上的可见性和仲裁关系，设 \(\alpha\) 是一个一致性标准。我们说 \(H, \vis \models \alpha\) 当且仅当：
- 对于 \(\alpha\) 中的每个 \(\tau \subseteq vis\)，\(\tau[so := \so, vis := \vis] \subseteq \vis\)，并且
- 如果 \(\total(vis) \in \alpha\)，则 \(\total(\vis)\) 成立。
进一步地说，我们说 \(H, \vis, \arb \models \alpha\) 当且仅当 \(H, \vis \models \alpha\) 并且 \(\vis \upharpoonright_{\Write} \subseteq \arb\)。
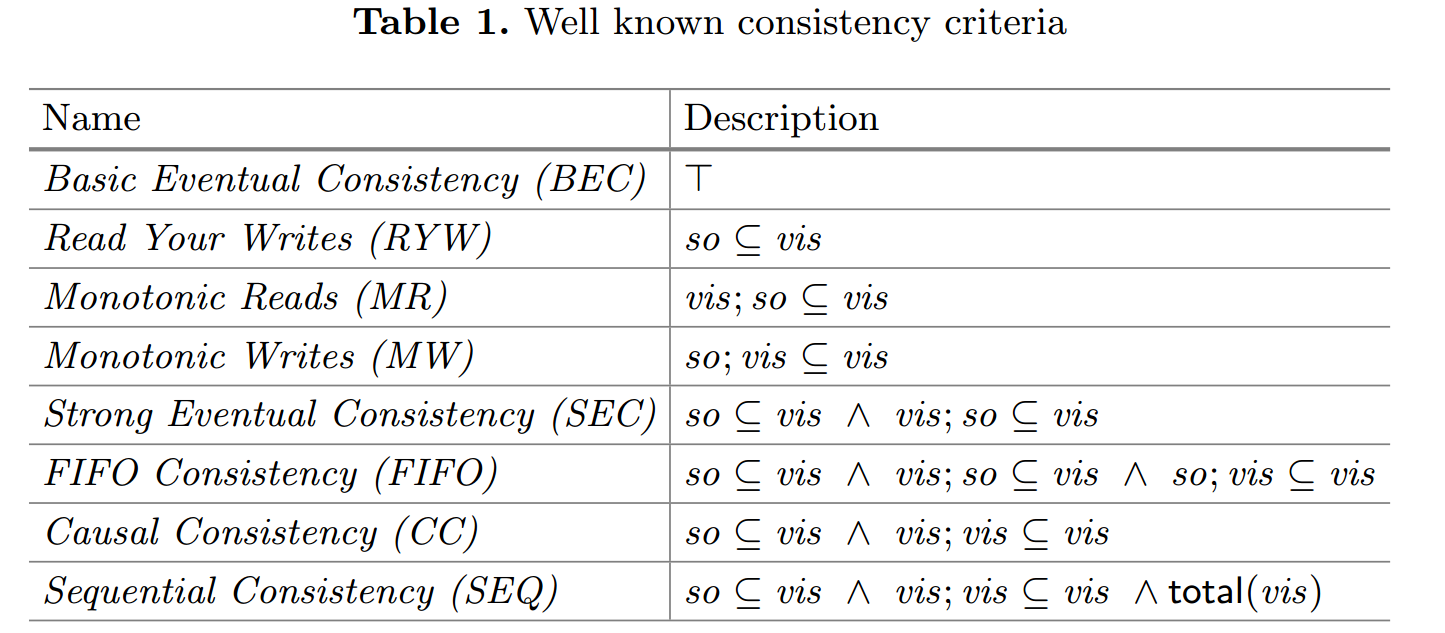
一些众所周知的一致性标准如表 1 所示。
我们说一致性标准 \(\alpha\) 至少和另一个一致性标准 \(\alpha'\) 一样强，如果对于每个历史 \(H\)、可见性关系 \(\vis\) 和仲裁关系 \(\arb\)，如果 \(H, \vis, \arb \models \alpha\)，那么 \(H, \vis, \arb \models \alpha'\)。
假设 \(H = (O, \so)\) 是一个混合历史。设 \(\alpha_w\) 和 \(\alpha_s\) 分别是弱一致性（wk）和强一致性（st）的标准。我们希望选择弱可见性关系 \(\vis_{\wk}\) 和强可见性关系 \(\vis_{\st}\)，以及仲裁关系 \(\arb\)，使得 \(H_{\wk}, \vis_{\wk}, \arb \models \alpha_w\) 并且 \(H_{\st}, \vis_{\st}, \arb \models \alpha_s\)。
正如我们在前一节中提到的，在多级设置中，单独满足对应于弱一致性和强一致性标准的约束是不够的。我们现在继续建模多级一致性约束。
Modelling Multilevel Consistency
受 DAX [1] 和现代处理器中的缓存层次结构的启发，我们可以将多级一致性建模为一系列按其保证的一致性递增顺序排列的数据存储，这样提供最弱一致性级别的数据存储最接近应用程序，而提供最强一致性级别的数据存储距离应用程序最远。我们进一步假设这些数据存储使用相同的仲裁策略来排序并发写入操作，并且每个较弱的数据存储都有能力更新其状态以匹配更强的数据存储的状态。
就本文而言，由于我们仅将自己限制在两个级别，即 \(\wk\) 和 \(\st\)，因此这将减少到只有两个数据存储，其中对应于较弱一致性标准的数据存储作为应用程序和对应于更强一致性标准的数据存储之间的缓存。
所有弱读操作都是从弱数据存储中执行的。
写操作有两种可能的执行方式：
- Write-Through：写操作首先在强数据存储中执行，最终将被传播到弱数据存储。
- Write-Back：写操作首先在弱数据存储中执行，最终将被传播到强数据存储。
强读操作有两种可能的执行方式：
- Read-Through: 在强数据存储中执行的强读操作的结果直接发送给应用程序，绕过弱数据存储。
- Read-Back: 强读操作的结果在传播到应用程序之前先在弱数据存储中更新。
因此，系统选择两种方式之一来执行写操作，并选择两种方式之一来执行强读操作。
请注意，选择 Write-Through 策略来执行写操作的系统将确保任何在弱数据存储中可见的写操作也将在强数据存储中可见，因为所有的写操作首先在强数据存储中执行，然后再传播到弱数据存储。因此，在弱读操作中可见的写操作的效果也将对后续的强操作可见。
同样，选择 Read-Back 策略来执行强读操作的系统将确保任何对强读可见的写操作也将在后续的弱读操作中可见。在返回强读结果给应用程序之前，该结果会合并到弱数据存储中。
然而，Write-Back 和 Read-Through 策略并不能提供任何关于在弱（或强）读操作中可见的写操作效果与同一会话中的后续强（或弱）读操作之间的保证。
我们现在以约束的形式定义这四种策略各自提供的保证。
定义 8（多级约束）
我们定义以下公式：
\[ \psi_{\thru}^{\write} \coloneqq (vis^{wk}; so) \upharpoonright_{\st} \subseteq vis^{st}\\ \psi_{\back}^{\write} \coloneqq \top\\ \psi_{\thru}^{\read} \coloneqq \top\\ \psi_{\back}^{\read} \coloneqq (vis^{st}; so) \upharpoonright_{\wk} \subseteq vis^{wk} \]
一个多级约束 \(\varphi\) 是形式为 \(\psi^{\read} \land \psi^{\write}\) 的合取式，其中 \(\psi^{\read} \in \{\psi_{\thru}^{\read}, \psi_{\back}^{\read}\}\) 和 \(\psi^{\write} \in \{\psi_{\thru}^{\write}, \psi_{\back}^{\write}\}\)。
Testing Multilevel Correctness of a Hybrid History
Bad Pattern Characterization for Multilevel Correctness
Constructing Minimal Visibility Relations
Complexity
Related Work
先前的研究表明，分布式数据存储需要提供多级一致性，以便在一致性和可用性/延迟之间取得平衡 [2,17,18,20]。Kraska 等人 [18] 的研究提供了一种事务范例，允许应用程序定义数据而非事务的一致性级别，还允许应用程序在运行时切换一致性保证。在 Guerraoui 等人 [17] 的研究中，作者提供了一个通用库，允许应用程序请求对同一查询的多个响应，其中较晚出现的响应比先前的响应更正确。因此，与较早的响应相比，较晚的响应应该对系统状态有更多的了解。在我们的工作中，我们定义了多级约束，它可以通过要求后续强响应看到先前弱响应观察到的效果来模拟增量一致性保证的要求。
Burckhardt [9] 提供了一种通用方法，用于在历史、可见性和仲裁顺序方面形式化分布式数据存储的规范，并为一致性标准提供了公理表征。在我们的工作中，我们基于这种形式主义推导出了读写存储的规范。我们调整了这种表征，将一致性标准定义为各个公式的结合。我们的工作在混合历史的定义方面扩展了 [9]，并为读写存储提供了多级正确性的定义。
之前已有关于验证行为相对于单个一致性标准的正确性的研究。示例包括 [7]，它涉及验证相对于最终一致性的正确性；[5]，它研究检查具有顺序规范的一致性标准的并发实现的可行性，包括顺序一致性、线性化和冲突可串行化；[6]，它侧重于因果一致性的正确性。我们的工作提供了一个通用程序，用于检查所有这些单个一致性标准的读写历史的正确性。此外，[6] 表明，验证历史相对于因果一致性的正确性是 NP-COMPLETE。但是，对于有区别的历史，该问题可以在多项式时间内解决。在我们的工作中，我们概括了计算最小可见性关系和检查使用我们的语法定义的所有一致性标准是否存在不良模式的技术。在 [12] 中，作者使用 Mazurkiewicz 踪迹理论对静态一致性进行建模。他们表明，历史记录的测试问题（他们称之为成员资格问题）是 NP-COMPLETE。我们无法在我们的框架中建模静态一致性，因为我们无法建模静态点。在 [14] 中，作者对根据各种一致性标准测试历史记录正确性的问题进行了详细的复杂性分析。我们的发现与 [14] 中关于测试一致性标准的难度的结果一致，该标准要求可见性关系为全序。在最近的一项研究 [13] 中，作者提供了一种根据弱一致性标准测试数据存储历史记录正确性的技术。该研究还根据扩展会话顺序（在那里称为程序顺序）和先发生关系（在 [9] 中称为先返回关系）的最小可见性关系来描述正确性。我们的工作将这一概念应用于读写存储，我们观察到，通过构建最小可见性关系可以满足可见性约束的正确性，而读写规范和仲裁约束的正确性可以简化为检查是否存在某些不良模式。特别是，我们根据冲突关系对仲裁关系的描述省去了 [13] 中使用的搜索所有可能的仲裁关系的步骤。
[16] 处理红蓝一致性的验证，其中在历史记录中，一部分操作被标记为红色，而其余操作被标记为蓝色。蓝色操作预计会满足较弱的一致性标准，而红色操作则应该满足更强的一致性标准。强操作和弱操作的效果是相互可见的。我们可以通过设置 \(\varphi = \psi^{\write}_{\thru} \land \psi^{\read}_{\back}\) 来对此进行建模。
我们的工作也应该与 [3] 形成对比，[3] 解决了根据 CRDT 规范检查其一致性的问题，并涵盖了广泛的 CRDT，包括复制集、标志、计数器、寄存器等。在我们的案例中，相关的数据结构是寄存器，结果是可比的（相对于较弱的一致性标准进行检查是可处理的）。然而，我们在本文中还考虑了具有多个一致性标准的寄存器，而那里没有考虑到这一点
另一项相关工作是 [4]，它使用读取关系（在那里称为写入读取关系）来显示测试执行（包含事务）的正确性，这些执行符合各种一致性标准，例如读取已提交 (RC)、读取原子 (RA)、因果一致性 (CC)、前缀一致性和快照隔离。当前工作的关键区别在于，我们同时考虑具有多个一致性级别的历史记录，而 [4] 在单个一致性标准下考虑由事务组成的执行。
