$$ \def\read{\mathsf{read}} \def\write{\mathsf{write}} \def\SER{\mathsf{SER}} \def\SI{\mathsf{SI}} \def\po{\mathsf{\textcolor{red}{po}}} \def\SO{\mathsf{\textcolor{purple}{SO}}} \def\VIS{\mathsf{\textcolor{orange}{VIS}}} \def\CO{\mathsf{\textcolor{orange}{CO}}} \def\WR{\mathsf{\textcolor{green}{WR}}} \def\WW{\mathsf{\textcolor{red}{WW}}} \def\RW{\mathsf{\textcolor{blue}{RW}}} \def\H{\mathcal{H}} \def\T{\mathcal{T}} \def\X{\mathcal{X}} \def\G{\mathcal{G}} \def\P{\mathcal{P}} \def\Int{\mathtt{Int}} \def\Ext{\mathtt{Ext}} \def\Session{\mathtt{Session}} \def\Prefix{\mathtt{Prefix}} \def\NoConflict{\mathtt{NoConflict}} \def\TotalVis{\mathtt{TotalVis}} \def\PreExecSI{\mathsf{PreExecSI}} \def\ExecSI{\mathsf{ExecSI}} \def\ExecSER{\mathsf{ExecSER}} \def\HistSI{\mathsf{HistSI}} \def\HistSER{\mathsf{HistSER}} \def\GraphSER{\mathsf{GraphSER}} \def\GraphSI{\mathsf{GraphSI}} \def\graph{\mathsf{graph}} \def\splice{\mathsf{splice}} \def\DCG{\mathsf{DCG}} $$
摘要
快照隔离(SI)是一种广泛使用的事务处理一致性模型,由大多数主流数据库和一些事务内存系统实现。不幸的是,它的经典定义是以低级操作方式给出的,通过理想化的并发控制算法,这使得对在 SI 下运行的应用程序的行为的推理变得复杂。我们给出了 SI 的替代规范,该规范根据 Adya 等人的事务依赖图对其进行了描述,概括了序列化图。与以前的工作不同,我们的描述不需要在依赖图中添加有关事务开始点和提交点的额外信息。然后,我们利用我们的规范来获得两种静态分析。第一个检查在 SI 下运行的一组事务何时可以分成更小的部分而不引入新的行为,以提高性能。另一个分析检查在 SI 减弱的情况下运行的一组事务是否与在 SI 下运行时的行为相同。
作者:
- Andrea Cerone, IMDEA Software Institute
- Alexey Gotsman, IMDEA Software Institute
INTRODUCTION
事务简化了并发编程,因为它允许对共享数据进行计算,这些计算与其他并发计算隔离,并且能够抵御故障。它们通常由数据库 [7] 提供,最近,事务内存系统 [22] 也提供这些功能。理想情况下,程序员希望获得有关事务计算隔离性的强有力保证,这可以通过可序列化的概念 [7] 来形式化:如果一组事务以某种顺序原子执行,则可以获得并发执行这些事务的结果。不幸的是,确保可序列化会带来严重的性能损失。因此,事务系统通常提供较弱的事务处理保证,这可以通过弱一致性模型来形式化。快照隔离 (SI) [6] 是最流行的此类模型之一,由主要的集中式数据库(例如 MS SQL Sever、Oracle)、分布式数据库 [14、27、29] 和事务内存系统 [1、8、15、25] 实现。
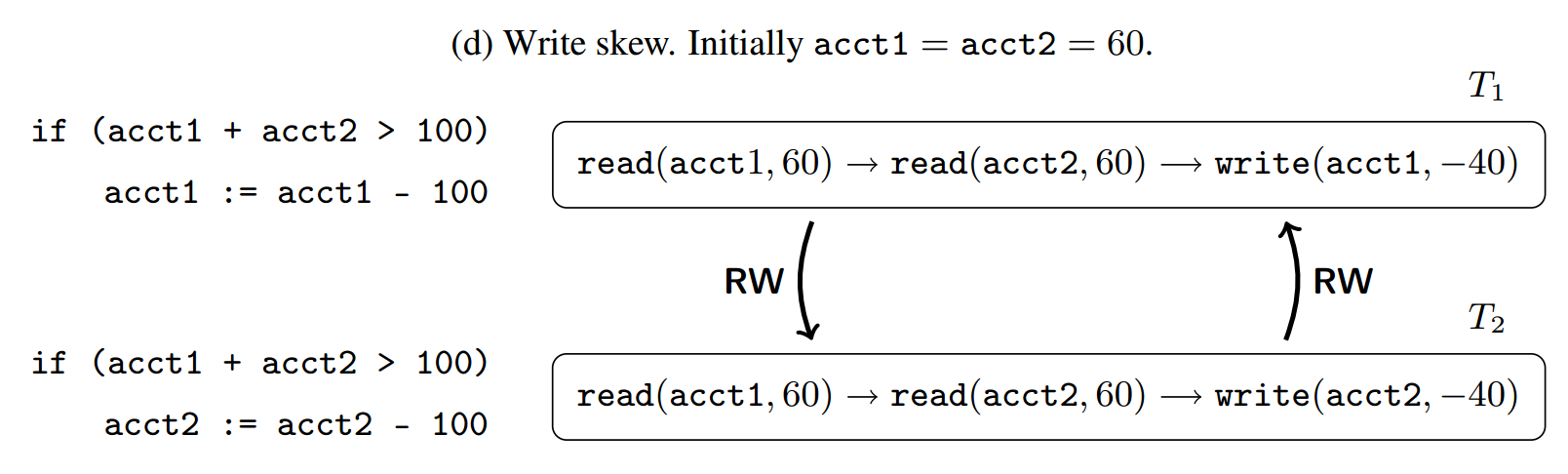
非正式地,SI 由多版本并发控制算法定义如下。事务 T 从其启动时拍摄的快照中读取共享对象的值。事务只有在通过写入冲突检测检查后才会提交:自 T 启动以来,没有其他已提交的事务写入 T 也写入的任何对象。如果检查失败,T 将中止。一旦 T 提交,其更改将对之后拍摄快照的所有事务可见。此并发控制算法允许不可序列化的行为,称为异常。其中之一,写偏斜,如图 2(d) 所示。事务 T1 和 T2 中的每一个都检查两个账户的总余额是否超过 100,如果是,则从其中一个账户中提取 100。在 SI 下,两个事务都可能通过检查并从不同的账户中提取,导致总余额为负数。在可序列化下不会发生这种结果。考虑到这样的异常,推断在 SI 下执行的应用程序的行为并非易事。由于 SI 的规范是通过并发控制算法以低级操作方式给出的,因此这项任务变得更加复杂。为了便于推理使用 SI 的应用程序并建立有关此一致性模型的有用结果,我们需要一个更具声明性的规范,尽可能多地从实现级细节中抽象出来。
Adya 等人 [2, 3] 提出了一种产生此类一致性模型规范的方法。在该方法中,一组事务的执行通过事务对 T1 和 T2 之间的三种依赖关系来描述:读取依赖关系记录 T1 读取 T2 写入的对象的值的情况;写入依赖关系记录 T1 覆盖 T2 写入的对象的值的情况;最后,以某种方式从读取和写入依赖关系派生出反依赖关系(§3)。一组事务及其之间的依赖关系形成依赖图,概括了经典的序列化图 [7]。然后,给定一致性模型允许的执行集由那些缺乏某些循环的依赖图定义;特别是,可序列化的执行以无环依赖图为特征。这种指定一致性模型的方式已被证明特别适合于设计静态分析 [12, 19, 23, 30, 38]、运行时监控 [9, 37] 和证明并发控制算法正确性 [16, 24, 36]。具体而言,依赖关系图方面的规范有助于在静态分析中探索可能的程序执行,因为分析可以通过在不同事务的代码中查找对同一对象的读写访问来确定运行时可能存在哪些依赖关系。相比之下,很难静态地预测有关事务执行的更低级信息,例如事务提交的顺序。
已经针对 ANSI 隔离级别(例如可序列化性、已提交读和可重复读 [2])以及最近的一致性模型提案提出了依赖图方面的规范 [5, 36]。但令人惊讶的是,没有这样的 SI 规范。这并不是因为缺乏尝试:Adya 确实提出了一个引用依赖图的 SI 定义 [2]。然而,为了捕捉 SI 的微妙语义,此定义通过描述有关事务执行的低级信息的关系扩展了依赖图,这抵消了它们的好处。
在本文中,我们首次仅从依赖图的角度对 SI 进行描述(§4),并将其应用于开发新的静态分析(§5 和 §6)。也就是说,我们表明 SI 完全允许依赖图所表示的执行,这些依赖图仅包含具有至少两个相邻反依赖边的循环。这一事实的证明非常重要,是本文的一项关键技术贡献。它需要证明,给定一个满足上述非循环条件的依赖图,我们可以构建某些关系来描述 SI 并发控制如何处理事务,例如事务提交的顺序。从事务依赖关系构建这些关系具有挑战性,我们证明的主要见解是通过这种构建过程给出的,该过程基于解决某些类型的关系不等式。
为了说明我们对 SI 的依赖图表征的好处,我们利用它来开发两种静态分析。首先,我们针对经典的事务切割问题 [4、30、35] 提出了一种新的静态分析——检查应用程序中的事务何时可以切割成更小的部分而不会引入新的行为 (§5)。当应用于在 SI 下执行的长时间运行的事务时,切割可以提高性能,因为 SI 事务运行的时间越长,由于写冲突而中止的可能性就越大。有针对可串行化 [30] 和并行 SI [12](最近提出的用于大型数据库的较弱版本的 SI [32])下的事务切割的分析。然而,尽管这种一致性模型被广泛使用,但在 SI 下还没有这样的分析。
我们对 SI 的依赖图表征有助于推导事务切割的静态分析,这不仅是因为可以静态确定可能的依赖关系。更详细地说,切割将程序中的事务转换为较小事务的会话 [14, 33](又名链 [38]),这确保事务将按给定的顺序执行,但不提供隔离保证。如果结果程序的每个 SI 执行都可以拼接成具有与原始执行相同操作的 SI 执行,但每个会话中的所有操作都在单个事务中执行,则切割是正确的。在 SI 上显示拼接执行的存在具有挑战性,因为选择其事务应提交的顺序并非易事。我们从事务依赖性方面对 SI 的表征避免了这种复杂性,因为与执行的低级方面不同,这些依赖关系在拼接过程中不会发生显着变化,这使得构建拼接执行变得容易。
我们考虑的另一种静态分析是检查应用程序是否对弱一致性具有鲁棒性 [19, 31]:无论它使用的是提供弱一致性模型的数据库还是提供更强一致性模型的数据库(§6),其行为都相同。在这种情况下,应用程序员可以获得使用较弱模型的性能优势,但可以推断出假设较强模型的应用程序的正确性。我们首先表明,我们的 SI 特性可以轻松推导出现有分析的变体,该分析检查在 SI 下执行的应用程序的行为是否与在可串行化下执行时的行为相同 [19](对 SI 的鲁棒性,§6.1)。然后,我们提出了一种新的静态分析,检查在最近提出的并行 SI [32] 下执行的应用程序的行为是否与在更强的传统 SI 下执行时的行为相同(对并行 SI 的鲁棒性,§6.2)。为了推导出这种静态分析,我们制定了并行 SI 的依赖图表征,这比传统 SI 更容易给出。同样,我们根据依赖图对一致性模型的表征极大地促进了上述鲁棒性分析的推导,因为这些表征使我们能够轻松地在不同模型上的执行之间进行映射。
由于篇幅限制,我们将一些证明推迟到 [11,§A]。
SNAPSHOT ISOLATION
定义 1
事务 $T = (E, \po)$,其中 $E$ 是事务集合,$\po$ 是程序顺序。
定义 2
历史 $\H = (\T, \SO)$,其中 $\SO$ 是会话序。
定义 3
执行 $\X = (\T, \SO, \VIS, \CO)$,其中 $\VIS$ 表示可见关系,$\CO$ 表示提交序。
定义 4
$$ \ExecSI = \set{\X | \X \models \Int \wedge \Ext \wedge \Session \wedge \Prefix \wedge \NoConflict} $$
$$ \ExecSER = \set{\X | \X \models \Int \wedge \Ext \wedge \Session \wedge \TotalVis} $$
$$ \HistSI = \set{\H | \exists \VIS, \CO.(\H, \VIS, \CO) \in \ExecSI} $$
$$ \HistSER = \set{\H | \exists \VIS, \CO.(\H, \VIS, \CO) \in \ExecSER} $$
简言之,一个历史可以对应多个执行,若其中一个执行满足 SI/SER 要求,则称该历史满足 SI/SER。
DEPENDENCY GRAPHS
定理 8
$$ \GraphSER = \set{\G | (\T_\G \models \Int) \wedge ((\SO_\G \cup \WR_\G \cup \WW_\G \cup \RW_\G) \ is \ acyclic)} $$
$$ \HistSER = \set{\H | \exists \WR, \WW, \RW.(\H, \WR, \WW, \RW) \in \GraphSER} $$
简言之,每个历史可能对应多个依赖图,每个依赖图可能对应多个执行。
SI CHARACTERISATION
定理 9
$$ \GraphSI = \set{\G | (\T_\G \models \Int) \wedge (((\SO_\G \cup \WR_\G \cup \WW_\G) ; \RW_\G ?) \ is \ acyclic)} $$
$$ \HistSI = \set{\H | \exists \WR, \WW, \RW.(\H, \WR, \WW, \RW) \in \GraphSI} $$
定理 10
$$ Soundness: \forall \G \in \GraphSI. \exists \X \in \ExecSI.\graph(\X) = \G $$
$$ Completeness: \forall \X \in \ExecSI. \graph(\X) \in \GraphSI $$
定义 11
元组 $\P = (\T, \SO, \VIS, \CO)$ 是 pre-execution,若其满足定义 3 的所有条件,除了 $\CO$ 是非全序的严格偏序。$\PreExecSI$ 是 pre-execution 的集合。
$$ \PreExecSI = \set{\P | \P \models \Int \wedge \Ext \wedge \Session \wedge \Prefix \wedge \NoConflict} $$

定理 12
$$ \forall \X \in \ExecSI . \VIS_\X \subseteq \CO_\X $$
定理 13
对依赖图 $\G = (\T, \SO, \WR, \WW, \RW)$,其中 $\T \models \Int$,且 $\VIS, \CO$ 无环,符合图 3 的不等式限制。则 $\P = (\T, \SO, \VIS, \CO)$ 是一个 pre-execution,且 $\P \in \PreExecSI$,且 $\graph(\P) = \G$。
推论 14
$$ \forall \X \in \ExecSI. \forall T, S \in \T_{\X}. S \xrightarrow{\RW_\X} T \iff S \neq T \wedge \ \exists x. S \models \read(x, _) \land T \models \write(x, _) \wedge \neg (T \xrightarrow{\VIS_x} S). $$
定理 15
对依赖图 $\G = (\T, \SO, \WR, \WW, \RW)$,对任意的 $R \subseteq \T \times \T$,
$$ \VIS = (((\SO \cup \WR \cup \WW) ; \RW ? ) \cup R)^∗ ; (\SO \cup \WR \cup \WW); $$
$$ \CO = (((\SO \cup \WR \cup \WW) ; \RW ? ) \cup R)^+ $$
是图 3 所示不等式的解,也是令 $\CO \supseteq R$ 的最小解。这意味着对于其他的解 $(\VIS', \CO')$ 且 $\CO' \supseteq R$,都有 $\VIS \subseteq \VIS', \CO \subseteq \CO'$ 。
TRANSACTION CHOPPING UNDER SI
这一节看不明白
在本节中,我们利用依赖图对 SI 的描述来推导静态分析,该分析检查在 SI 下执行的应用程序中的交易何时可以切分为 [30] 较小交易的会话而不会引入新行为(在这种情况下,会话也称为链 [38])。为此,分析必须检查应用程序的任何具有切分交易的 SI 执行是否可以拼接成具有与原始执行相同操作的 SI 执行,但每个会话中的所有操作都在单个交易中执行。我们首先建立一个动态切分标准,检查依赖图表示的单个 SI 执行是否可拼接。然后,我们由此推导出静态分析,检查给定切分应用程序产生的所有执行是否都是这种情况。
在历史 $\H$ 中,用 $\approx_\H$ 等价关系表示两个事务在同一线程内。用 $\boxed T_{\H} = (E, \po)$ 表示将 $T$ 在 $\H$ 中所属会话中的所有事务拼接成单个事务的结果,其中 $E = ( \bigcup \set{E_S \mid S \approx_{\H} T})$ 是所有事务的事件集的并集,$\po$ 描述这些事件的先后顺序:
$$ \po = \set{ (e, f) \mid (\exists S. e, f \in E_S \land e \xrightarrow{\po_S} f \land S \approx_{\H} T) \lor (\exists S, S'. e \in E_S \land f \in E_{S'} \land S \xrightarrow{\so_{\H}} S' \land S' \approx_{\H} T) } $$
我们定义 $\splice(\H)$ 为在历史 $\H$ 中拼接所有会话所得到的历史:$\splice(\H) = \left( \set{ \boxed{T}{\H} \mid T \in \T{\H} }, \emptyset \right)$。一个依赖图 $\G \in \GraphSI$ 是可拼接的,如果存在一个依赖图 $\G' \in \GraphSI$ 使得 $\H_{\G'} = \splice(\H_{\G})$。对于一个依赖图 $\G$,我们定义 $\approx_{\G} = \approx_{\H_{\G}}$ 并且 $\boxed{T}{\G} = \boxed{T}{\H_{\G}}$。
简言之,拼接就是把同一个线程内的事务合并,拼接后的历史没有 $\SO$ 关系。
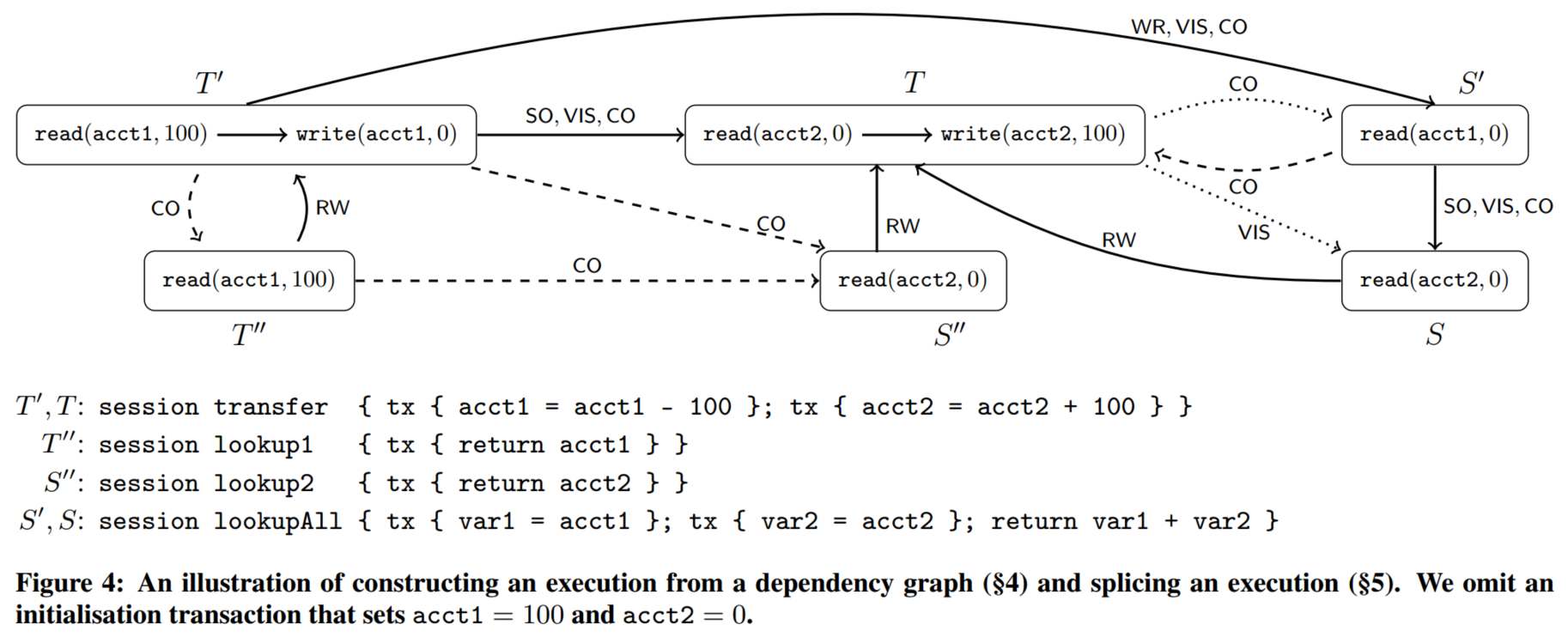
例如,图 4 中的图 $\G_1$ 不是可拼接的,因为 $\splice(\H_{\G_1}) \notin \HistSI$。非正式地,$\boxed{S}{\G_1}$ 观察到 $\boxed{T}{\G_1}$ 写入到 $\mathtt{acct1}$,但没有写入到 $\mathtt{acct2}$。另一方面,让 $\G_2$ 是通过从 $\G_1$ 中移除事务 $S$ 和 $S'$ 得到的图。那么 $\G_2$ 是可拼接的,如图 $\G_2 \in \GraphSI$ 所示,$\H_{\G_2} = \splice(\H_{\G_2})$ 并且只有边 $\boxed{T''} \xrightarrow{\RW_{\G_2}} \boxed{T_{\G_2}}$ 和 $\boxed{S''} \xrightarrow{\RW_{\G_2}} \boxed{T_{\G_2}}$。
给定一个依赖图 $\G$,我们定义对应于 $\G$ 的动态切片图(dynamic chopping graph)为 $\DCG(\G)$,通过移除 $\approx_{\G}$ 相关事务之间的 $\WR_{\G}$、$\WW_{\G}$ 和 $\RW_{\G}$ 边,并用会话序的反序 $\SO_{\G}^{-1}$ 扩展 $\G$ 的边。我们将后者的边称为前驱边,将 $\SO_{\G}$ 中的边称为后继边,将 $\WR_{\G} \cup \WW_{\G} \cup \RW_{\G} \setminus \approx_{\G}$ 中的边称为冲突边。动态切片图 $\DCG(\G)$ 中的一个循环是关键的,如果:
- 它不包含两次出现的同一个顶点;
- 它包含“冲突、前驱、冲突”边的三个连续片段;并且
- 任何两个反依赖边($\RW_{\G} \setminus \approx_{\G}$)在循环中至少被一个读($\WR_{\G} \setminus \approx_{\G}$)或写($\WW_{\G} \setminus \approx_{\G}$)依赖边分隔开。
我们的动态切片标准如下:
定理 16
对于 $\G \in \GraphSI$,若 $\DCG(\G)$ 不包括关键边,则 $\G$ 是可拼接的。
ROBUSTNESS CRITERIA FOR SI
我们现在考虑另一种类型的静态分析,检查应用程序是否能够抵御弱一致性:在弱一致性模型下执行它会产生与在强一致性模型下执行它相同的客户端可观察行为。
Robustness against SI
我们首先表明,我们的 SI 特性允许推导出现有分析的变体,该分析检查在 SI 下执行的应用程序的行为是否与在可序列化性 [19](对 SI 的鲁棒性)下执行时的行为相同。为此,分析检查应用程序代码可能不会在 $\HistSI \setminus \HistSER$ 中产生历史记录。与事务斩断(§5)一样,我们首先建立一个动态鲁棒性标准,检查由依赖图表示的单个执行是否在 $\GraphSI \setminus \GraphSER$ 中。这很容易从定理 8 和 10 得出。
定理 19
$\G \in \GraphSI \setminus \GraphSER$ 当且仅当 $\T_\G \models \Int$ 且 $\G$ 中有环且所有环包含至少两个相邻的 $\RW$ 边。
我们可以从定理 19 中得出静态分析,其方式与 §5 中类似。即,分析假设应用程序中的事务代码由具有给定读写集的一组程序 $\P$ 定义。基于这些集合,它构建一个静态依赖图,过度近似程序 $\P$ 执行中可能存在的依赖关系。然后,分析检查该图是否没有至少两个相邻反依赖边的循环。根据定理 19,这意味着程序 $\P$ 在 $\HistSI \setminus \HistSER$ 中不产生任何历史记录,因此相应的应用程序对 SI 具有鲁棒性。请注意,一致性模型的依赖图表征极大地促进了上述静态分析的推导,因为这些表征使我们能够轻松地在具有相同历史记录的不同模型上的执行之间建立对应关系。
Robustness against parallel SI towards SI
RELATED WORK
快照隔离最初是由一个理想化的算法定义的,该算法是根据实现级概念制定的 [6]。从那时起,出现了更具声明性的 SI 规范的提案 [2、10、28],其中之一 [10] 是我们的出发点(§2)。但是,这些规范是以关系的形式陈述的,这使得获得诸如事务切割和稳健性分析之类的结果变得具有挑战性。
Fekete 等人 [19] 提出了我们在 §6.1 中考虑的针对 SI 的稳健性的分析。为此,他们证明了一个大致相当于我们的完整性结果(定理 10(ii))的事实,但他们没有建立与我们的健全性结果(定理 10(i))类似的结果。后者更具挑战性的结果是获得 SI 下事务切割分析和针对 SI 的并行 SI 的稳健性分析所需的结果:两者都需要证明具有特定依赖图的执行在 SI 中,而不是相反。我们还希望我们对 SI 的规范将对依赖关系图有用的其他领域有益,例如运行时监控 [9, 37] 和证明并发控制算法的正确性 [16, 36]。最后,我们希望在我们的可靠性定理的证明中从事务依赖关系构建总提交顺序的方法可用于为其他一致性模型提供依赖关系图特征,这些模型的公式包含类似的全序,例如前缀一致性 [34]。
我们用来表征 SI 的依赖关系图约束也出现在 Lin 等人的工作中 [24],他们用它来制定条件,在这些条件下,复制数据库保证 SI,前提是其每个副本都这样做。与他们相比,我们解决了一个更一般的表征 SI 的问题,无论它是如何实现的,并处理不需要事务来查看最新快照的 SI 变体。
事务斩断最近受到了广泛关注。特别是,研究人员已经证明,在可序列化的情况下执行时,Web 应用程序中出现的事务可以以某种方式进行斩断,从而大大提高其性能 [26, 36, 38]。也有人提出了事务内存一致性模型,这些模型以类似于斩断的方式削弱了一致性保证 [4, 20, 35]。我们的斩断分析能够将这些好处带给提供 SI 的事务系统。我们之前曾提出过并行 SI 的斩断分析 [12],它也依赖于此一致性模型的依赖图表征(定理 21)。但由于并行 SI 可以在不使用 SI 提交顺序的类似物的情况下进行表述,因此其依赖图表征并没有带来我们在建立健全性定理时必须应对的挑战。

