摘要
我们提出了假装同步(pretend synchrony),这是一种验证分布式系统的新方法,基于这样的观察:虽然分布式程序必须异步执行,但在验证它们的正确性时,我们通常可以将它们视为同步的。为此,我们计算了一个同步(synchronization),一个在语义上等效的程序,其中所有发送、接收和消息缓冲区都被简单的赋值取代,产生了一个可以使用 Floyd-Hoare 风格的验证条件和 SMT 进行验证的程序。我们实现了我们的方法作为在 Go 中编写经过验证的分布式程序的框架,并通过四个具有挑战性的案例研究对其进行评估——经典的两阶段提交、Raft 领导者选举协议、单法令 Paxos 协议和基于 Multi-Paxos 的分布式键值存储。我们发现假装同步允许我们开发高性能系统,同时通过将手动指定的不变量减少 6 倍来使功能正确性的验证更简单,并通过将检查时间减少三个数量级使之更快。
导论
异步分布式系统很难做到正确。网络延迟、执行时间的变化和消息丢失可能会触发程序员既不打算也不预期的行为。为了消除这种微妙的错误来源,程序员煞费苦心地构建工作负载和压力测试来调整相关的时间表。这些努力注定会失败。由于无界数据域和程序经常参数化的事实,即参与节点的数量在编译时是未知的,可能的调度数量是无限的,确保测试充其量只是触及所有可能行为的表面。确保正确性的更原则性方法是通过数学证明正式验证它们的预期属性。然而,验证说起来容易做起来难。由于通信的异步(asynchronous)特性,程序员必须向证明者提供不变量,这些不变量通过在所有参与者的联合状态上拆分案例来明确枚举可能的调度。这样的不变量很复杂,很难预测。更糟糕的是,异步不变量必须对(无界)消息缓冲区的内容进行推理,这使得甚至无法确定候选不变量的正确性。
Lipton 简化(Lipton's reduction)为驯服异步提供了一条诱人的途径。 直观地说,它为将每个接收移动(moving)到其匹配的发送操作提供了基础,从而将这对异步操作融合到一个同步分配中(assignment)。 几位作者已经探索了如何使用这个想法来简化推理,例如关于原子性以允许共享内存程序的正确性证明,并推理消息传递系统中的死锁。 不幸的是,一些具有挑战性的问题共同阻碍了简化的应用,特别是在分布式环境中融合发送和接收。
- 广播(Broadcasts):我们必须考虑广播到其他进程集并因此从其他进程集接收的进程集。例如,像 Paxos 或 Raft 这样的系统有一组提议者广播到一组接受者。这些广播打败了简化:当实际顺序取决于运行时的不同交错时,我们如何将发送集融合到接收集?
- 丢弃(Drop):我们必须考虑到消息在网络上被丢弃,或者等效地,延迟任意长时间。这些丢弃阻止了简化:我们如何将接收与发送融合,其有效负载甚至可能无法通过网络?
- 轮次(Rounds):最后,分布式执行通常在概念上构造为多轮执行的迭代。例如,我们可能在领导者选举协议中有多个轮次(或投票),或者由分布式存储中的后续密钥查找触发的不同轮次通信。这些轮次阻碍了简化:即使实际上可能会收到延迟消息并干扰未来的轮次,我们如何才能仅在一轮内融合发送和接收?
我们的关键见解是,通过仔细的语言设计,我们可以确保惯用且高效的分布式程序具有足够的语义结构以实现简化,从而简化形式验证。 尤其是,
- 对称进程标识符足以命名组成参与广播的集合的各个进程。我们可以通过使用标量集数据类型来明确对称性,它只允许进程标识符之间的相等比较。至关重要的是,即使广播可能以不同的顺序接收,对称性确保了这些顺序是等效的,以进程标识符的排列为模,从而允许我们通过标准的聚焦和模糊(或实例化和概括)操作来减少多进程广播抽象解释理论。
- Scala Actors 或 Go 中的类型化通道有助于确保在任何时候,一个进程都在期待单一类型的消息,并且在一对进程之间最多有一个给定类型的消息。我们观察到这个属性让我们可以将消息丢弃简单地视为返回 None 消息的超时接收操作。这直接让我们合理地减少了对 Maybe 消息分配的发送和接收。
- 轮标识符允许我们在程序语法中明确轮的概念,特别是将重复计算构造为对无限轮集的迭代。
然后,我们可以使用这种结构来定义称为轮非干扰的独立概念,该概念受循环并行化的经典工作的启发,直观地确保不同的轮是通信封闭的。 这允许我们利用轮次的对称性来简化在所有轮次上证明一个断言的问题,从而在一个任意选择的轮次上证明该断言,这可以使用 Lipton 的简化来完成。
- 库:我们的第一个贡献是程序员可以用来实现异步分布式系统的类型和通信原语库。我们库的设计确保将通信结构化为类型化的通道,即使在存在消息丢失、广播和多轮交互的情况下也能减少通信—现实世界分布式系统的基本特征(第 3 节)。
- 编译器:我们的第二个贡献是将程序编译成它们的同步的算法。我们将该编译器构建为一组本地重写规则,每个规则都将输入程序转换为一个新程序,包括一个同步的前缀和一个仍需要重写的后缀。至关重要的是,我们引入了新颖的重写规则,该规则利用我们的库所解释的通信结构,在存在消息丢失、广播和多轮通信的情况下实现语法指导的减少。我们确定了一类称为分层成对通信协议 (SPCP) 的程序,编译器对其是完整的,即编译器保证计算同步,如果存在同步(第 4 节)。
- 验证器:我们的第三个贡献是展示如何使用同步作为验证的基础。我们证明了每次重写都保留了程序的停止状态的稳健性结果(定理 4.4)。然后,我们实现了一个验证器,它以语法指导的方式遍历同步程序,以组合代码和断言以发出 Owickie-Gries 样式验证条件,其有效性—通过 SMT—与健全性结果一起确定,意味着原始来源的正确性(第 6 节)。
- 评估:我们的最后贡献是假装同步作为
的实现:一个用 Go 编写经过验证的分布式程序的框架。我们使用 开发了四个案例研究:经典的两阶段提交协议、Raft 领导者选举协议、单法令 Paxos 协议和基于 Multi-Paxos 的分布式键值存储。为了证明我们的库允许惯用的实现,我们在 Multi-Paxos 上构建了一个键值对存储,并展示了它的性能以与其他实现竞争。为了证明我们的同步编译器有助于正确性验证,我们展示了所有这些协议都具有简单直观的同步不变量, 会自动检查。为了证明假装同步简化了验证,我们还在 Dafny 中实现了除键值存储之外的所有案例研究,并使用最先进的 IronFleet 使用的经典方法来验证它们系统。我们发现假装同步将手动指定的不变量注释的数量减少了 6 倍。根据我们的经验,事实证明,由 验证的同步断言对于确定 Dafny 验证所需的许多异步不变量至关重要。此外,通过避免复杂的量化不变量(在消息缓冲区的内容上),假装同步将检查程序所需的时间缩短了三个数量级,从使用 Dafny 的 20 多分钟到不到 2 秒(第 7 节)。
概述
我们首先在高层次上激发假装同步,然后展示一系列小例子来说明其基本成分。
网络和故障模型:我们的正式开发和基准测试假设网络中的消息可能会被任意丢弃或重新排序。 我们通过非阻塞接收对此类消息进行建模,这些接收可以不确定地超时并返回 None 值。 此外,我们假设一个标准的崩溃恢复失败模型,其中一个进程可能会崩溃,但该进程必须将其状态保存在持久存储中,并从该持久状态恢复执行,或者保持沉默。静默相当于所有进程消息被网络丢弃。但是,为了简化本概述中的演示,我们将假设所有接收都是阻塞的,并且消息不能被丢弃,但可以任意重新排序。
动机:假装同步
两阶段提交
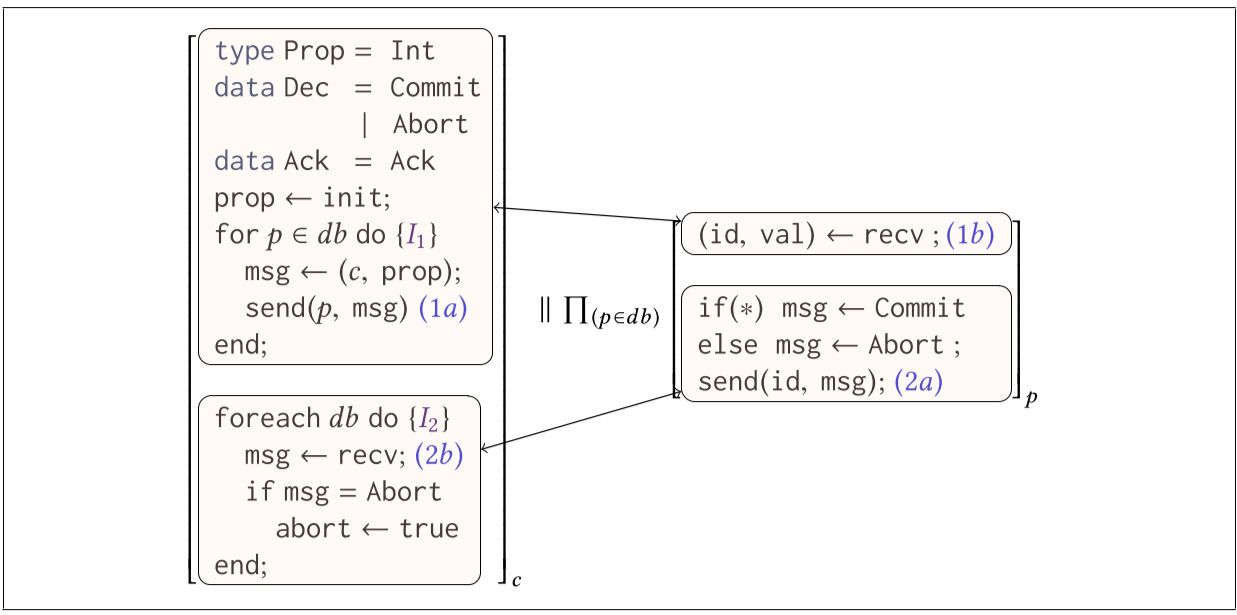
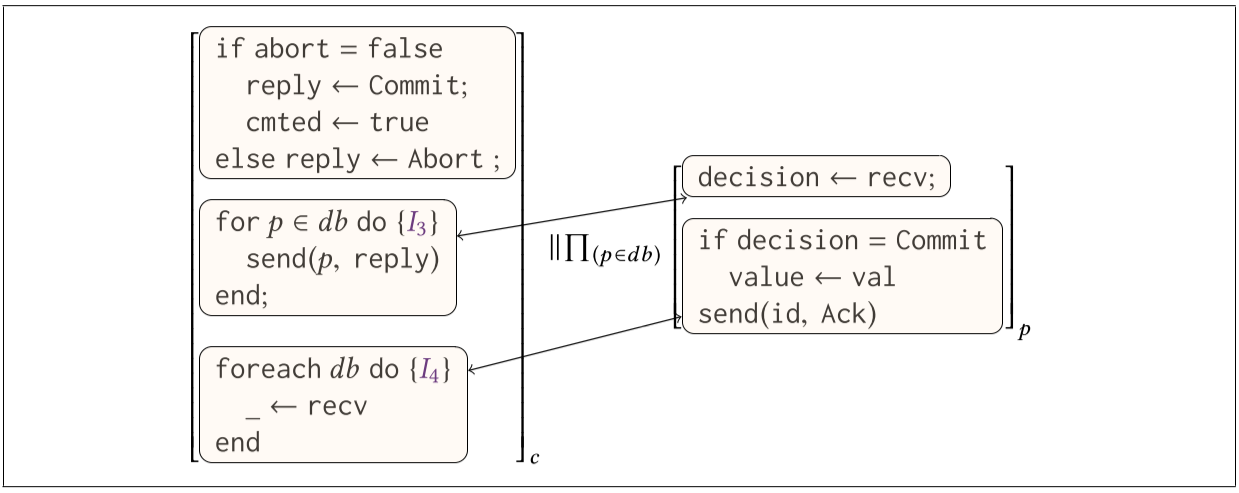
图 1 和图 2 显示了经典的两阶段提交 (2PC) 协议。在该协议中,协调节点 c 尝试将值提交给多个数据库节点 db。我们使用
正确性
为了证明我们实现 2PC 的正确性,我们想证明,如果协议完成并且协调者决定提交事务,则所有数据库节点确实选择了提议的值,即,在协议之后必须满足以下条件:
异步不变量很复杂
让我们首先考虑如何在异步设置中证明此属性。考虑图 1 中协调者的第一个循环,让 done 表示到目前为止已在位置 (1a) 执行发送的所有数据库节点的集合。为了排除消息出现在“稀薄的空气”中,我们需要断言只要
- 有一条从 c 到 p 的正在进行的消息,其中包含 c 的进程 id 和提案值,并且 p 正在等待接收消息(已发送,但未接收)
- p 收到 c 的消息,将其 val 变量设置为 prop 并决定要么提交或中止事务,但尚未响应(已接收并决策,但未响应)
- p 响应,将其决定转发给 c(已响应)
对于图 1 中 c 的第二个循环,我们需要一个类似的分情况讨论:如果
- 有一条从 c 到 p 的未决消息包含 c 的进程 id 和提议(已发送)
- p 已选择提交或中止但没有尚未发送响应(已接收并决策,但未响应)
- p 已发送包含提交或中止消息的响应
最后,如果
异步使验证无法确定
虽然避免这种分类讨论——在协调者、数据库节点和消息缓冲区的联合状态上——本身是可取的,但在异步设置中证明正确性还有一个更基本的问题:直接包含消息通过将其建模为数组来缓冲到系统状态需要嵌套数组读取,这使得即使检查候选不变量也无法确定异步使验证无法确定虽然避免这种情况分裂——在协调者、数据库节点和消息缓冲区的联合状态上——本身是可取的,但在异步设置中证明正确性还有一个更基本的问题:通过将消息缓冲区建模为数组来直接将消息缓冲区包含到系统状态中需要嵌套数组读取,这使得甚至检查候选不变量也无法确定。
假装同步
在本文中,我们确定了一种建立在以下观察基础上的新方法:即使程序在执行时表现得异步,我们可以在推理程序时完全假装通信是同步的。例如,考虑图 1 中标记为 (1a) 的发送,并假设在当前迭代协调者 c 发送到某个进程 p。由于在我们的执行模型中,消息由通过网络发送的值的类型来索引,因此消息只能在单个接收(single receive)时接收,即在图 1 中标记为 (1b) 的位置处的接收(图 2 中的接收需要一个 Decision 类型的值)。此外,发送不会干扰 c 和 db 中其他进程之间的所有发送。因此,在不影响我们正确性属性的有效性的情况下,我们可以通过 Lipton 的推动者理论 [Lipton 1975],假装提案在发送后直接被接收。对于图 1 中位置 (2a) 处的 p 发送,可以进行类似的论证。即使 p 的发送匹配多个接收(即,在 p 的循环中位置 (2b) 处的任何接收),由为 a 选择特定获胜者所产生的状态给定的迭代是对称的,即,是等效的模数过程标识符的排列。因此,只要我们保留所有可能的迭代顺序,我们就可以在不影响正确性的情况下匹配发送和接收。
同步不变量很简单
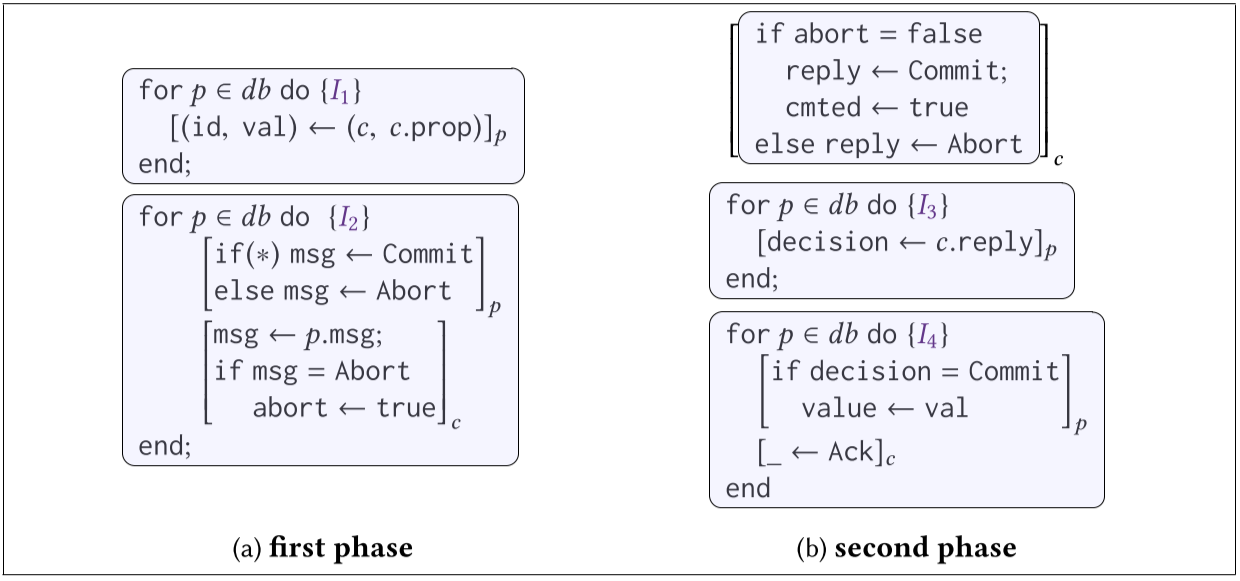
我们的方法通过以下方式利用了这种洞察力:用户不是为异步程序编写不变量,而是像程序是同步的一样编写不变量,有效地将匹配的发送和接收对视为赋值。同步不变量作为 for 循环的注释给出。再次考虑图 1。对于第一个循环,我们需要以下不变量
不变量
总之,这些简单的同步不变量没有考虑到异步所需的分类讨论,足以证明 2PC 的正确性。
检查同步不变量
我们分两步验证同步不变量的正确性。首先,我们计算同步(synchronization);一个语义等价的同步程序,通过迭代地应用一组重写规则(第 4 节)。其次,我们使用 synchronization 来生成和检查验证条件,以确保所提供的不变量是归纳的、无干扰的并且暗示了所需的正确性属性(第 6 节)。在第一步中,我们的实现完全自动地计算这种同步,而不依赖于用户提供的不变量。每个重写步骤都会生成一个新程序,其中包含一个同步的前缀和一个仍需要重写的后缀。重复此过程,直到后缀减少为 skip。图 3 显示了
主要观点
我们现在讨论假装同步背后的主要成分,并说明它们如何实现异步分布式程序的同步验证。
Ex 1:简化

将程序视为同步进行推理大大简化了验证,但是我们什么时候可以在不影响我们要验证的正确性属性的有效性的情况下同步程序呢?如果我们限制自己证明有关停止状态的属性,那么对于给定的跟踪,我们总是可以通过 Lipton 的减少理论将发送移动到匹配的接收,从而使发送完全同步。考虑图 4a 中所示的示例 Ex1。进程 p 在一组静态无界进程 qs 上循环。对于 qs 中的每个进程 q,p 发送一个 ping 消息并等待 q 的确认。 qs 中的每个进程都等待接收一个值,将该值分配给 v,最后以一个确认应答。我们想证明,在终止后,qs 中的所有进程都将其变量 v 设置为 ping,即我们希望 ∀q ∈ qs : q.v = ping 在终止时保持不变。为此,我们首先注意到,对于每个 q ∈ qs,q 的接收只能与单个发送(p 中的那个)匹配。此外,我们要证明的属性并不涉及中间程序状态,例如消息缓冲区的内容。因此,我们可以通过将发送和接收对转换为赋值,将程序完全重写为更简单的同步版本。对 q 的发送和 p 的接收执行类似的步骤会产生图 4 所示的同步程序。然后,以下不变量证明了预期的属性。这个不变量表明,每当循环遍历一个进程时,它的 v 变量就会被设置为 ping。
请注意,如果我们要验证原始异步程序,这个简单的不变量是不够的; 相反,我们必须对是否已收到消息进行区分大小写,并维护消息缓冲区的不变量(即,从 p 到 qs 中的进程的所有消息都包含值 ping)。
Ex 2:对称

我们可以将发送向上移动到它的匹配接收,不仅如果在所有程序跟踪中都存在唯一匹配接收,而且如果所有匹配接收都是对称的,即从选择特定接收产生的状态等同于排列进程 ID [Norris IP 和 Dill 1996]。考虑图 5a 中的 Ex2。进程 p,首先向 q 中的所有进程发送 ping 消息,然后在第二个循环中等待它们的确认。和前面的例子一样,我们想证明,在终止时,qs 中的所有进程都将它们的 v 变量设置为 ping。为此,考虑过程 p 的第一个循环。与前面的示例一样,p 向位置 (1a) 的某个进程 q 的发送只能在一次接收时接收,即在位置 (1b) 的进程 q 的接收。因此,我们可以将原始的异步程序重写为图 5b 中的中间程序。该中间程序由对应于第一循环的同步的同步前缀和待同步的余数组成。
接下来,考虑 p 的第二个循环。对于给定的循环迭代,p 在位置 (2b) 的接收可以从位置 (2a) 的 qs 中的进程的多个发送接收。但是,所有发送都是对称的。也就是说,进程运行相同的代码,但进程 ID 不同,因此,为每次迭代选择任意获胜者会导致相同的最终状态。这产生了图 5c 所示的同步程序。尽管 Ex2 结构的通信方式与 Ex1 不同,但同步正确性证明不受影响。因此,我们可以重用相同的不变量,即 I5 来证明所需的正确性。
Ex 3:组播
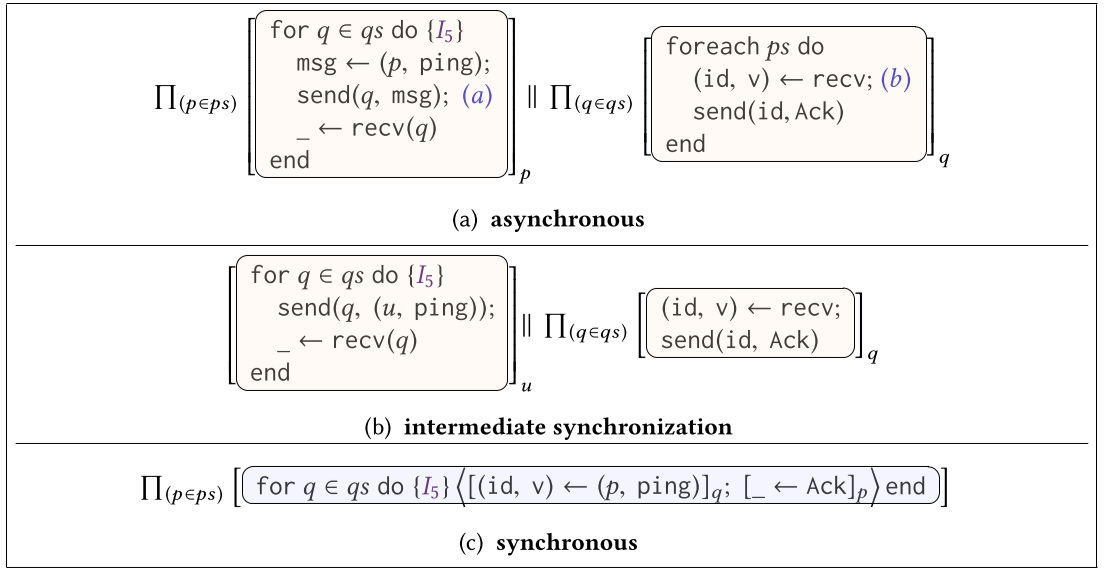
不幸的是,简化和对称本身不足以验证真实的分布式系统。考虑图 6a 中的 Ex3,它是 Paxos 协议 [Lamport 2001] 的“提议”阶段的简化。这里,一组进程 ps 正在与一组进程 qs 进行通信。 ps 中的每个进程 p 循环 qs 中的所有进程。对于 qs 中的每个进程 q,p 发送一个由它自己的进程标识符和值 ping 组成的对。类似地,qs 中的每个进程 q 循环遍历 ps 中的所有进程。在每次迭代中,q 从 ps 中的某个进程接收一个 id 和一个值 v,然后向该 id 发送一个确认。和前面的例子一样,我们想证明,在程序执行后,qs 中的每个进程都将其局部变量 v 设置为值 ping。不幸的是,我们不能直接应用上一个例子的推理,因为 Ex3 中的比赛不是对称的!例如,考虑在位置 (b) 接收 qs 中的某个进程 q。对于给定的循环迭代,进程 q 可以从位置 (a) 处的 ps 中的所有进程接收,但是,这些进程可能处于不同的循环迭代中,因此,一般来说,选择另一个可能会导致不同的结果。为了克服这一困境,我们将注意力集中在 ps 中的单个过程与 qs 中的过程的任意迭代之间的交互。即使整个系统存在非对称竞争,p 中的单个进程和 qs 中的所有进程之间的每次交互都是对称的。因此,我们说 Ex3 的竞争几乎是对称的,并通过以下方式利用这一洞察力:为了计算整个系统的同步,同步 ps 中的单个进程与所有进程 qs 之间的交互就足够了,然后并行重复单个交互,对 ps 中的每个进程执行一次。重要的是,与前面的示例相比,同步不再是顺序程序,而是进程 ps 上的并行组合。图 6b 显示了单个进程 u ∈ ps 与 qs 中每个进程的任意迭代之间的交互。由于这种交互与 Ex2 中的相同,我们获得了图 6c 中所示的整体同步,其中我们使用⟨P⟩ 表示 P 是原子执行的。最后,我们注意到,尽管通信模式要复杂得多,但仍可以通过简单的同步不变 I5 证明预期的属性。
Ex 4:消息丢失
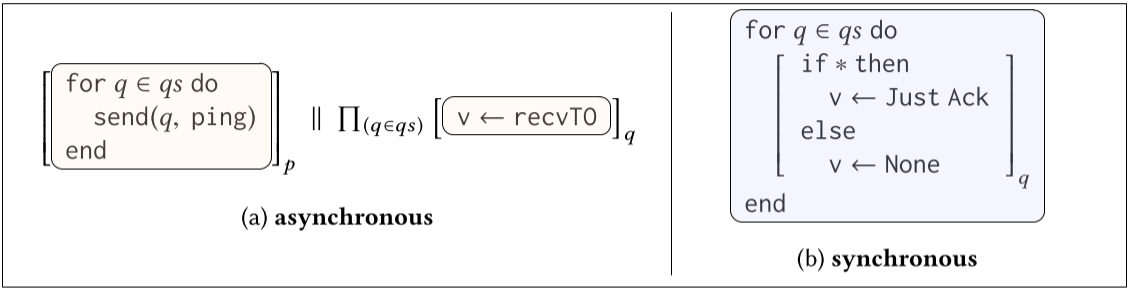
验证分布式系统的一个关键困难是消息可以被网络丢弃。在这样的设置中,接收必须能够超时以避免无限期地等待丢失的消息。但是,由于无法判断消息是否实际上已被丢弃,或者只是延迟,这会产生接收陈旧消息的可能性(即那些用于较早接收但过早超时的消息)。因此,异步设置中的正确性证明必须表明陈旧的消息不会影响所需的属性。假装同步的语言限制了以下通信不变量,这使得对消息丢失的推理变得容易:在任何给定时刻,一个进程需要单一类型的消息,并且在给定进程对之间最多有一个给定类型的消息,即,每个可能的发件人只有一个匹配的消息。鉴于此限制,我们可以将接收与超时同步,该接收期望来自某个固定的其他进程的消息,而不必担心在同一通道上接收到陈旧的消息,但是,我们不是立即分配接收到的值,而是区分是否消息已被删除。我们可以通过调用对称推理将这种推理推广到我们期望来自一组进程的消息的情况,就像以前一样。考虑图 7 中的示例 Ex4,其中进程 p 向集合 qs 中的每个进程发送 ping 消息。 qs 中的每个进程都使用非阻塞接收来等待消息。这个接收或者将接收到的值分配给一个可能类型的 Just 给变量 v,或者不确定地超时,在这种情况下它分配 None。图 7b 显示了 Ex4 的同步:同步循环 qs 中的所有进程,并将 ping 分配给 q 的局部变量 v,或者 p 不确定地将 Just Ack 或 None 分配给 w。
Ex 5:多轮
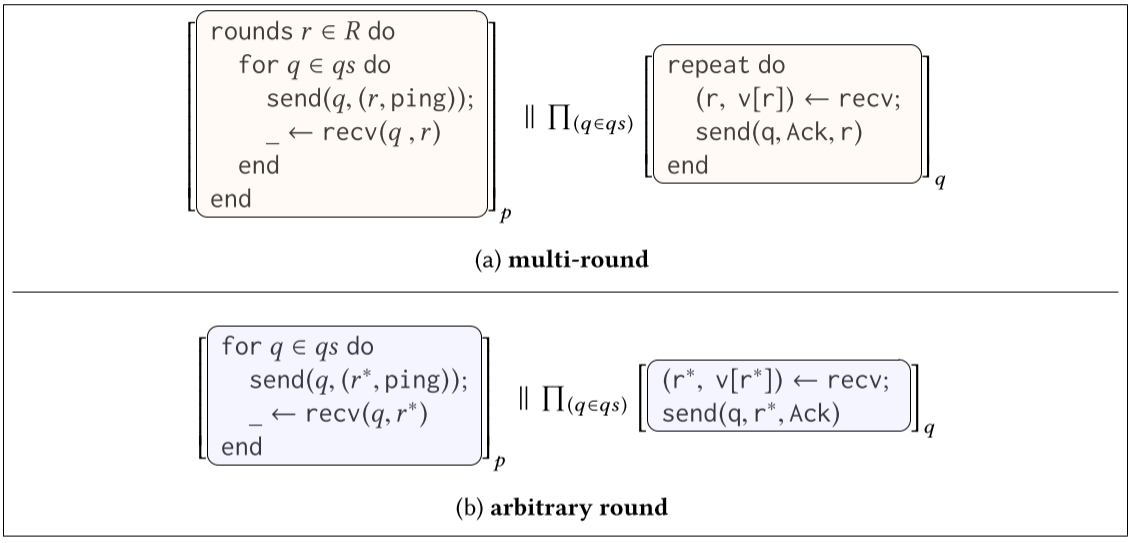
接下来,我们讨论如何使用轮次重复协议。考虑图 8 中的 Ex5,它使用轮次重复图 4a 中的 Ex1 的协议。为此,进程 p 使用循环 rounds r ∈ R do P end 为集合 R 中的每个轮标识符 r 迭代 P 一次。 q 中的每个进程使用重复语句重复其协议,该语句永远循环。在每一轮中,进程 p 遍历 qs 中的进程,并向每个 q 发送一个由轮数 r 和一个 ping 组成的对。然后它等待来自同一进程的回复,它只接受当前轮 r 中的值。 qs 中的每个进程都等待一个值和一个整数。当它接收到消息时,它将轮数绑定到 r,将接收到的值分配给由当前轮索引的映射 v,最后以对轮 r 的确认进行响应。在 2.2 中,我们想证明变量 v 在协议终止时被设置为 ping,然而,现在我们想证明这个属性在所有轮次中都成立。更正式地说,我们想证明 ∀r ∈ R : ∀q ∈ qs : v[r] = ping 在协议完成后成立。为了证明这个性质,我们首先观察 Ex5 表现出我们所说的圆形不干涉。轮不干扰要求 1) 不同轮对应的迭代不通过共享状态相互干扰,即写入或读取同一个变量;2) 不同轮对应的迭代不通过发送消息进行干扰。示例 Ex5 满足这两个条件:对应于不同轮的迭代不共享状态,因为每个进程只访问由其当前轮数 r 索引的 v。类似地,在 Ex5 中,对应于不同轮次的迭代不会相互发送消息,因为 p 和所有 qs 只发送和接收当前绑定轮数 r 的消息。由于 Ex5 表现出圆形不干涉,我们可以证明 ∀r ∈ R : ∀q ∈ qs : v[r] = ping 对所有迭代都成立,通过证明该属性适用于单个任意迭代。(第 5 节中的定理 5.4)。图 8b 显示了 Ex5 对任意轮 r* 的实例化,这让我们可以重用不变量 I5 来证明所需的属性。
表达能力
为了计算同步,
分布式消息传递程序
图 9 显示了 IceT 的语法,这是一种用于分布式消息传递程序的命令式语言。 IceT 作为一种中间语言,

语法
分布式进程
每个分布式进程都与一个唯一标识符 (ID) 相关联,该标识符用作发送消息的地址。 标识符属于标量集数据类型,即只能比较是否相等。我们用 skip 表示空进程,用
程序
我们从单个进程语句的顺序和并行组合中获得程序。 我们允许对同一进程的连续语句进行分组,即对于语句 s1 和 s2,我们将
我们使用
范式
如果一个程序由来自不共享变量的不同进程的语句序列的并行组合组成,则该程序属于范式(Normal Form),即,在范式程序中,进程不能与其自身并行组合。对于两个这样的程序 P 和 Q,我们让
语义
接下来,我们描述 IceT 程序的行为。
发送和接收
进程通过发送和接收消息进行通信。语句
不变量
在 IceT 中,每个 for 循环都用循环不变量
原子动作和选择
该语言包括原子动作
语义
属性
属性
停止属性和不变性
在本文中,我们关注验证程序的停止属性,即停止状态的属性,即没有进程可以采取任何进一步步骤的状态。 暂停属性的示例范围从局部断言安全到全局属性,例如死锁自由度或两阶段提交中的协议(参见公式 2.1)。
我们写
我们写
几乎对称的竞争
我们的方法要求程序只包含几乎对称的竞争(almost symmetric races)。为了检查给定程序的这个属性,我们首先用一个唯一的标签(tag)来注释每个语法发送语句。对于每个语法接收,我们然后计算它可以接收的标签集(set of tags)。为了确定一个程序是否只包含几乎对称的竞争,我们要求,对于每个语法接收,它可以接收的标记集必须最多包含一个语法发送语句。虽然通常很难计算给定语法接收可以从中接收消息的发送标签集,但我们使用发送和接收消息的类型通过将所有发送与正确类型相加来计算合理的过度近似、round 和发送者规范到集合(例如,在第 2.1 节提案中,决策和确认具有不同的类型,从而确保它们只能在正确的位置接收)。这提供了一个简单的语法检查。
消除通配符接收
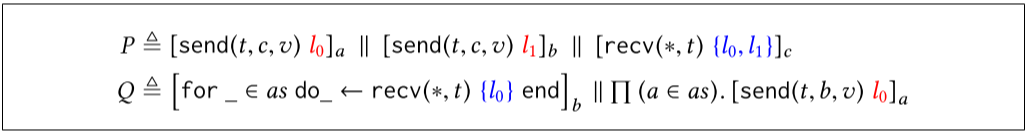
如果一个程序只包含几乎对称的竞争,我们可以很容易地消除通配符接收,方法是用来自唯一相应进程的接收或对称的 ID 集替换它们。
示例 3.1:考虑图 10 中所示的程序 P 和 Q。发送用红色标记注释,接收用蓝色标记集注释。P 中的接收违反了几乎对称竞争的属性,因为它可以返回由 a 或 b 发送的消息。在 Q 中,c 中的接收可以从 as 中的任何进程接收消息,但每条消息都源自标记为
确保一个程序只包含几乎对称的竞争,再加上我们的语言限制,为我们提供了以下关键保证:每当一个进程期望来自一个固定的其他进程的固定类型和轮次的消息时,最多可以有一个这样的消息。这个属性来自对称种族的定义和我们的语言限制的事实
确保相同(

