降维(Dimensionality Reduction)
我们假设数据能够在低维空间被表示
高维数据在低维空间的表示是更加高效的。
SVD 示例
r 表示保留的特征值的数量
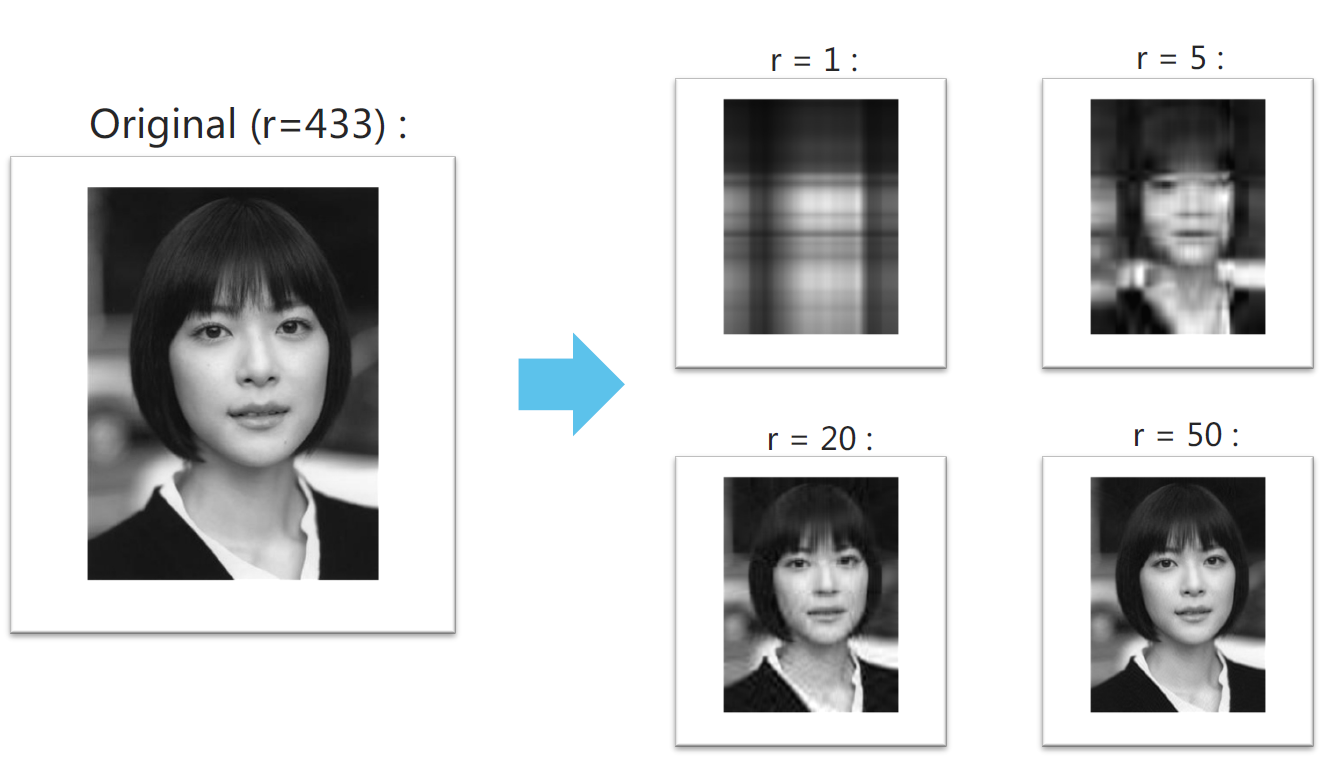
压缩/降低尺寸
- \(10^6\)行,\(10^3\)列,不更新
- 随机访问一行数据,很少的错误时可以接受的
如下的矩阵其实是个二维矩阵,我们通过缩放 \([1,1,1,0,0]\) 或 \([0,0,0,1,1]\) 可以重建所有的行。
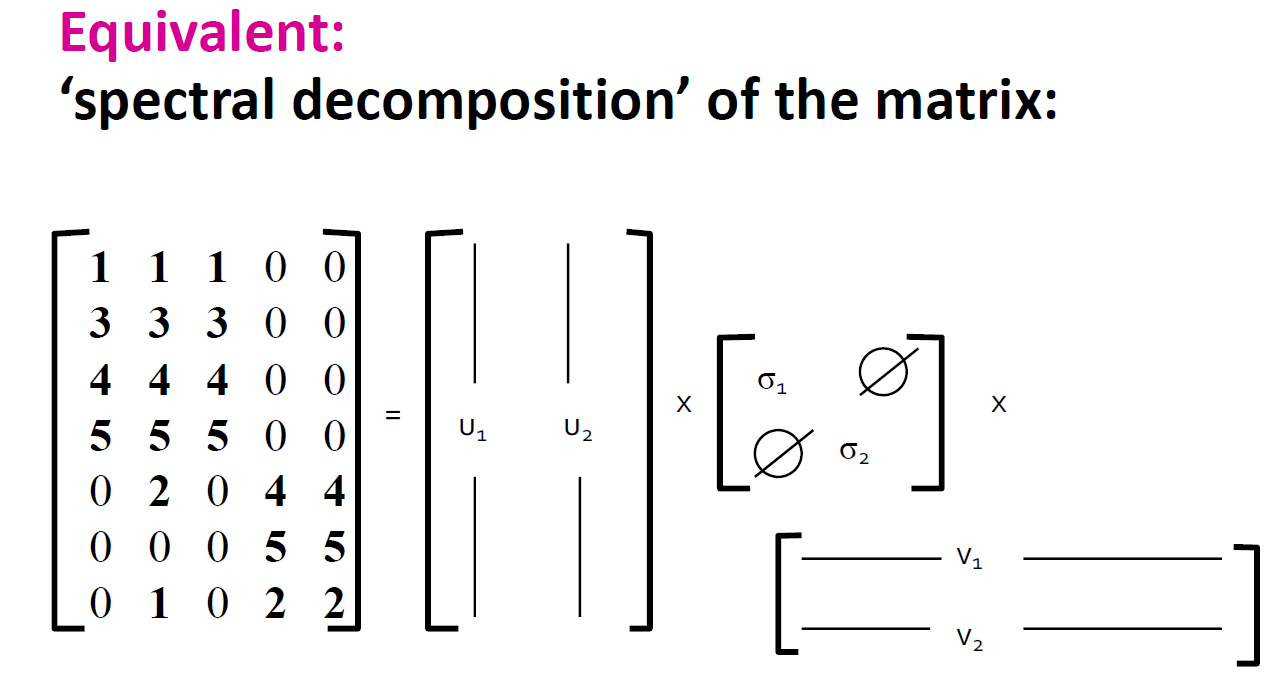
矩阵的秩
- 什么是矩阵 A 的秩?A 的线性独立列数
- 例子:
\[ A = \begin{bmatrix} 1 & 2 & 1 \\ -1 & -3 & 1 \\ 3 & 5 & 0 \\ \end{bmatrix}\ Rank(A) = 2 \]
秩是可以降维
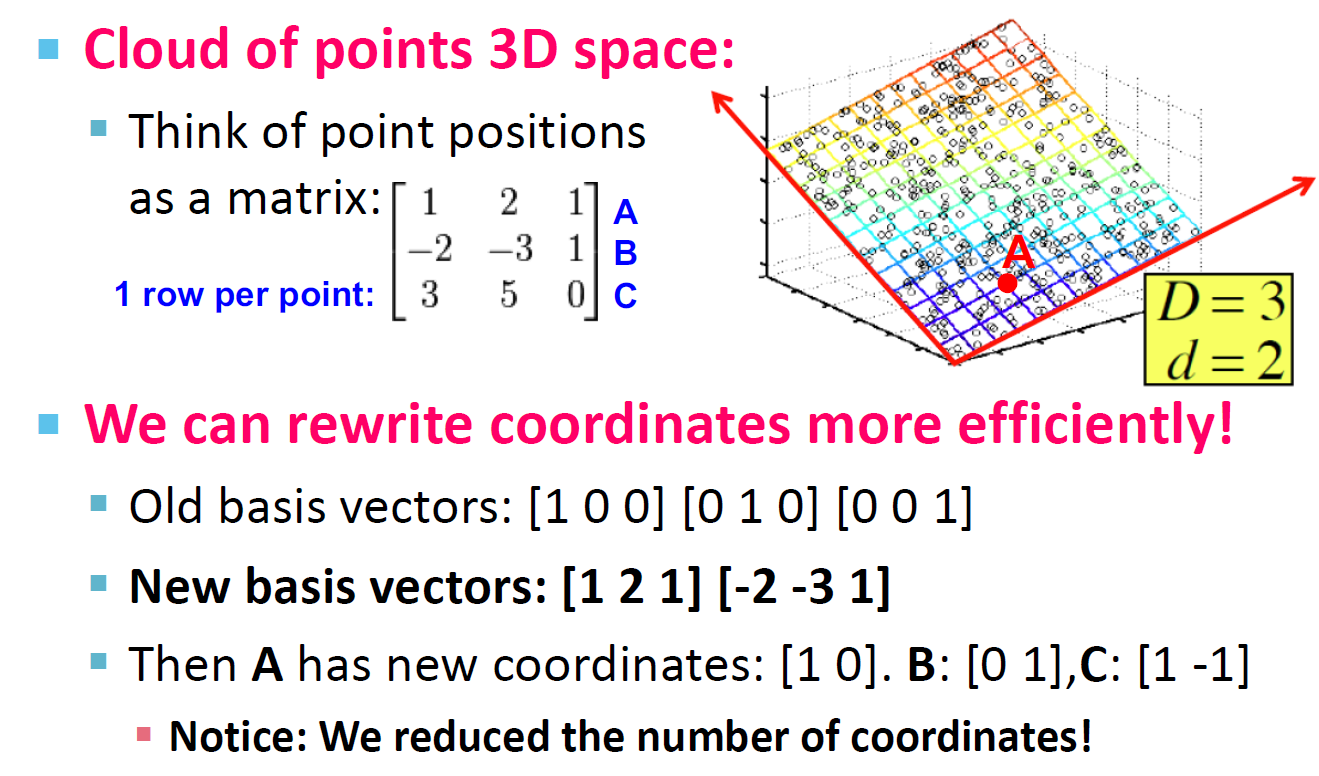
我们可以通过 \([1,2,1][-2,-3,1]\) 两个向量来重写矩阵 A,A 的新坐标为:\([1,0][0,1][1,-1]\)。
降维的目的
- 数学上是发现数据中的轴
- 发现隐藏的联系和主题:比如经常一同出现的单词等
- 移除相似和噪声特征:并不是所有单词都是有用的
- 数据解释和可视化
- 更容易处理和存储数据:(找到规律,压缩数据量)
降维的描述
与用两个坐标表示每一个点不同,我们用轴上的坐标表示每一个点(对应红线上点的位置)。
通过这样做,我们会产生一些错误,因为这些点并不完全在直线上(信息损失),需要我们考虑我们是否可以接受这部分信息损失。
SVD
奇异值的值必然为正
SVD 的分类
| 标准 SVD(无失真) | 近似 SVD |
|---|---|
 |
 |
SVD 的介绍
变量(维数)较多,增加了分析问题的复杂性。
数据丰富但知识贫乏:实际问题中,变量之间可能存在一定的相关,因此,多变量中可能存在资讯的重叠。
人们自然希望通过克服相关、重叠性,用较少的变量来代替原来多的变量,而这种代替可以反映原来多个变量的大部分资讯,这实际上是一种“降维”的思想。
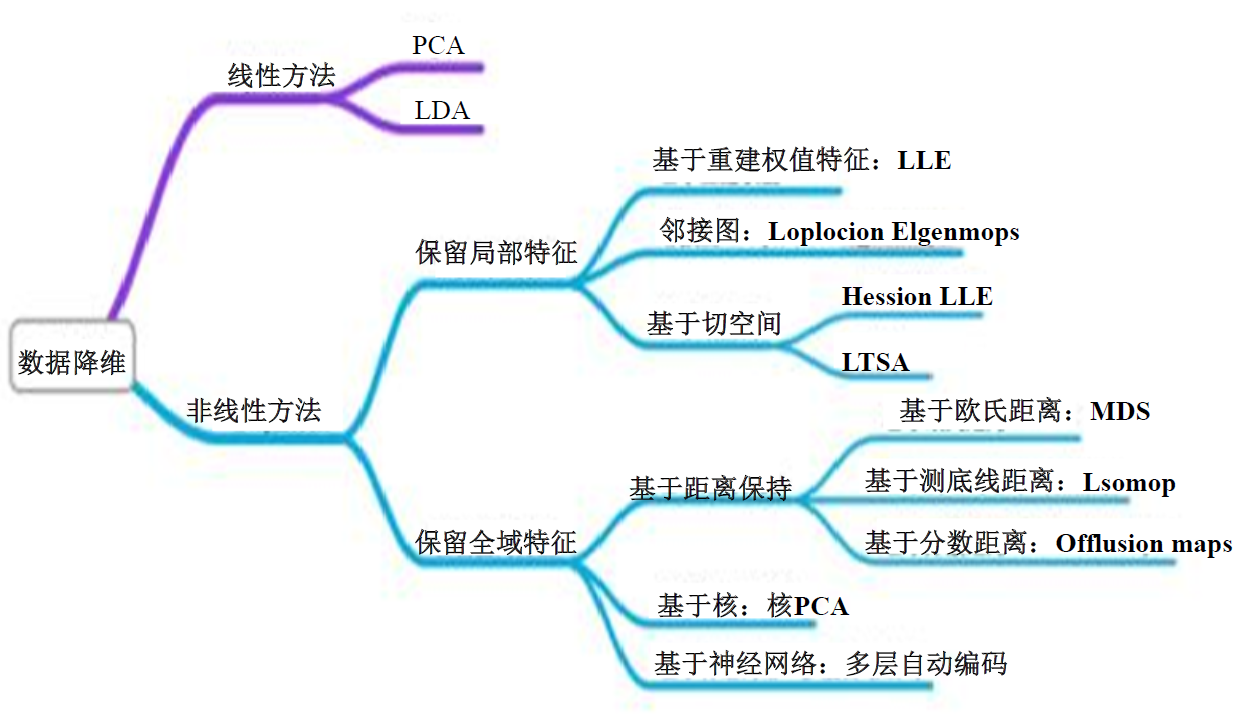
降维方法汇总
特征值与特征向量
- 设 \(A\) 是 \(n\) 阶矩阵,如果数 \(\lambda\) 和 n 维非零列向量使关系式\(Ax = \lambda x\)成立
- 则称\(\lambda\)是方阵 A 的特征值,非零向量 x 称为 A 的对应特征值的特征向量。
- 一般求解方法
\[ |A - \lambda I| = 0 \iff \begin{vmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ . & . & ... & . \\ a_{n1} & a_{n2} & ... & a_{nn} \\ \end{vmatrix} = 0 \]
降维方法
- PCA(主成分分析,Principal-Component Analysis)
- LDA(线性判别分析)
- 因子分析
- SVD(奇异值分解,Singular-Value Decomposition)
- CUR 分解
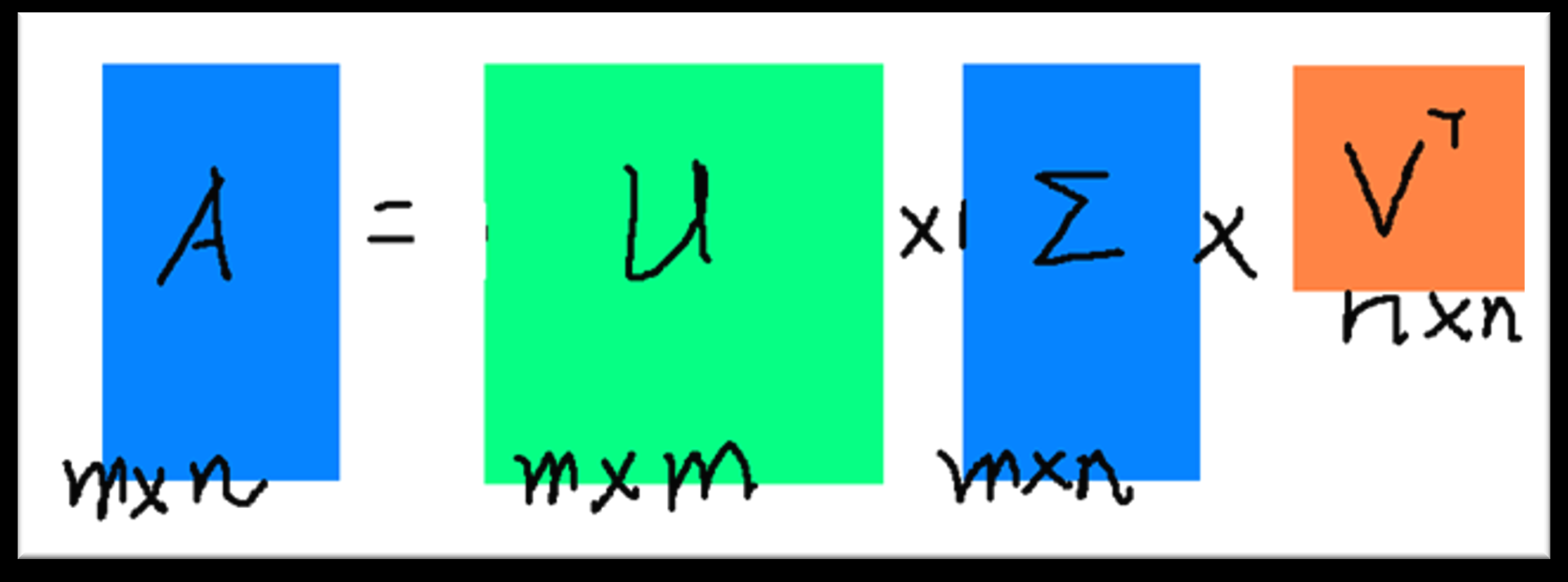
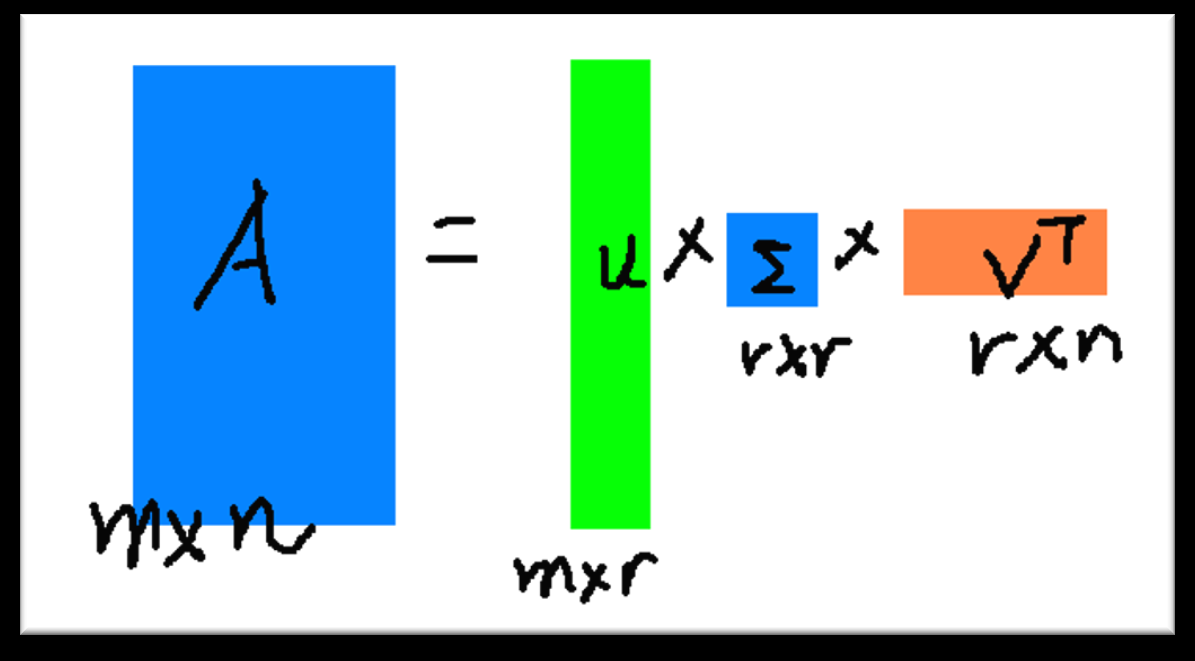
SVD(奇异值分解,Singular-Value Decomposition)
\[ A_{[m * n]} = U_{[m * r]} * \Sigma_{[r * r]} (V_{[n * r])^T} \]
| 矩阵符号 | 矩阵名称 | 矩阵描述 |
|---|---|---|
| \(A\) | 输入数据矩阵 | m * n 维 |
| \(U\) | 左奇异矩阵 | m * r 维,正交矩阵,\(UU^T = I\) |
| \(\Sigma\) | 奇异值对角矩阵 | r * r 维,r 是矩阵 A 的秩,只有对角线上有值,其他元素均为 0 |
| \(V\) | 右奇异矩阵 | n * r 维,正交矩阵,\(V^TV = I\) |
Notes:奇异值分解的信息下降是非常快的,基本上前 100 个奇异值就可以表征大多数的数据。
SVD 图示
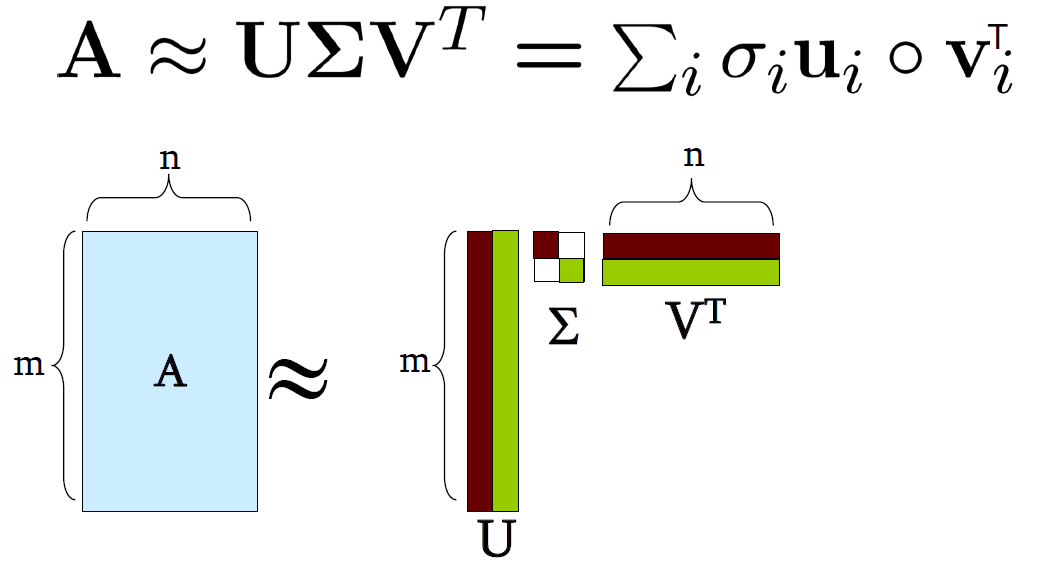 |
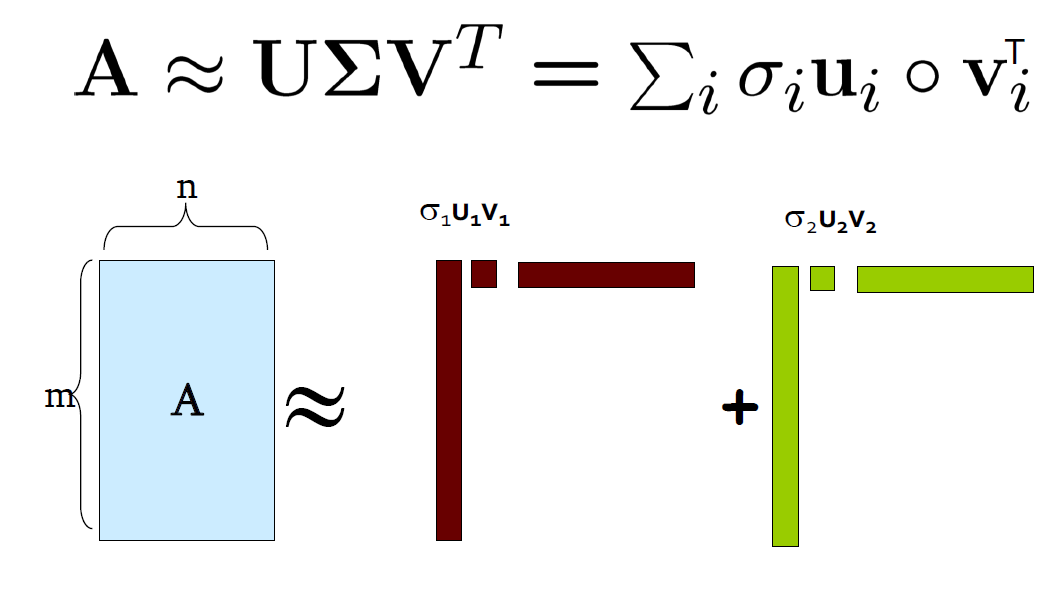 |
|---|
奇异值求解
\[ AA^T = U\Sigma V^TV\Sigma^TU^T = U\Sigma\Sigma^TU^T \tag{1-1} \]
\[ A^TA = V\Sigma U^TU\Sigma V^T = V\Sigma^T\Sigma V^T \tag{1-2} \]
我们通过简单分析可以知道 \(AA^T\) 和 \(A^TA\) 是对称矩阵
- 我们利用上面的(1-1)式来进行特征值分解,得到的特征矩阵就是 U
- 通过上面的(1-2)式来进行特征值分解,得到的特征矩阵就是 V
- 对 \(\Sigma\Sigma^T\) 或者 \(\Sigma^T\Sigma\) 中的特征值开方,可以获得所有的奇异值
SVD 计算示例
\[ A = \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{bmatrix} \ A^T = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \end{bmatrix} \]
求解特征值要从大到小排列
| 矩阵名 | 矩阵值 | 特征值 | 特征矩阵 |
|---|---|---|---|
| \(U\) | \(U = A * A^T = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 1 & 1\end{bmatrix}\) | \(\lambda_1 = 3, u_1 = (\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}})^T\) \(\lambda_2 = 1, u_2 = (\frac{1}{\sqrt{2}}, 0, -\frac{1}{\sqrt{2}})^T\) \(\lambda_3 = 0, u_3 = (\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})^T\) |
\(\begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}\) |
| \(V\) | \(V = A^T*A = (\begin{matrix} 2 & 1 \\ 1 & 2\end{matrix})\) | \(\lambda_1 = 3,v_1 = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) ^ T\) \(\lambda_2 = 1,v_2 = (-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) ^ T\) |
\(\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix}\) |
求解奇异值为:\(\sqrt{3}\) 和 1
SVD 的性质
我们通常可以将一个实数矩阵 A 按照分解为\(A = U\Sigma V^T\)
- \(U,\Sigma,V\):唯一
- U,V:列正交
- \(U^TU = I,V^TV = I\),I 是单位矩阵
- 列是正交单位向量
- \(\Sigma\):对角矩阵:对角值(奇异值)为正,并以降序排列
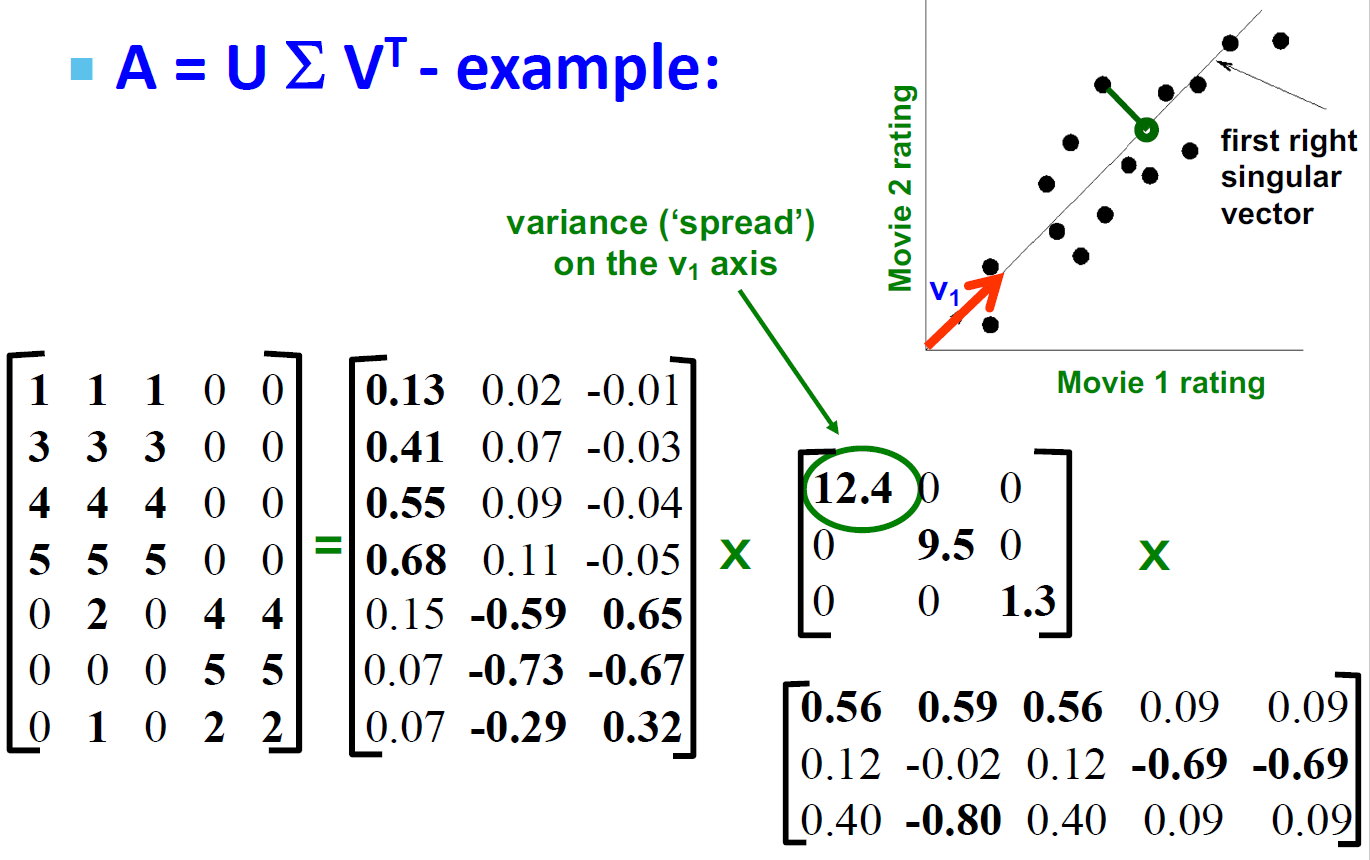
SVD 的例子的解释(Users to Movies)
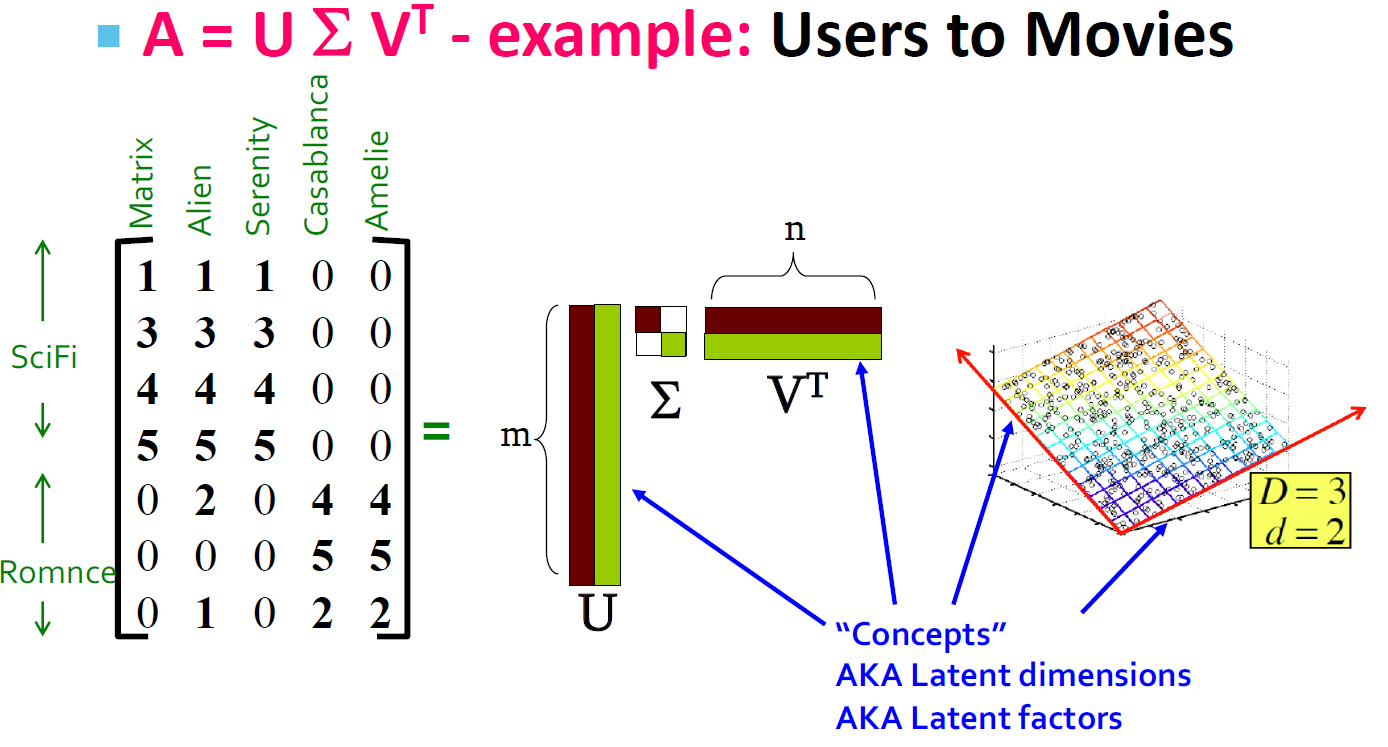

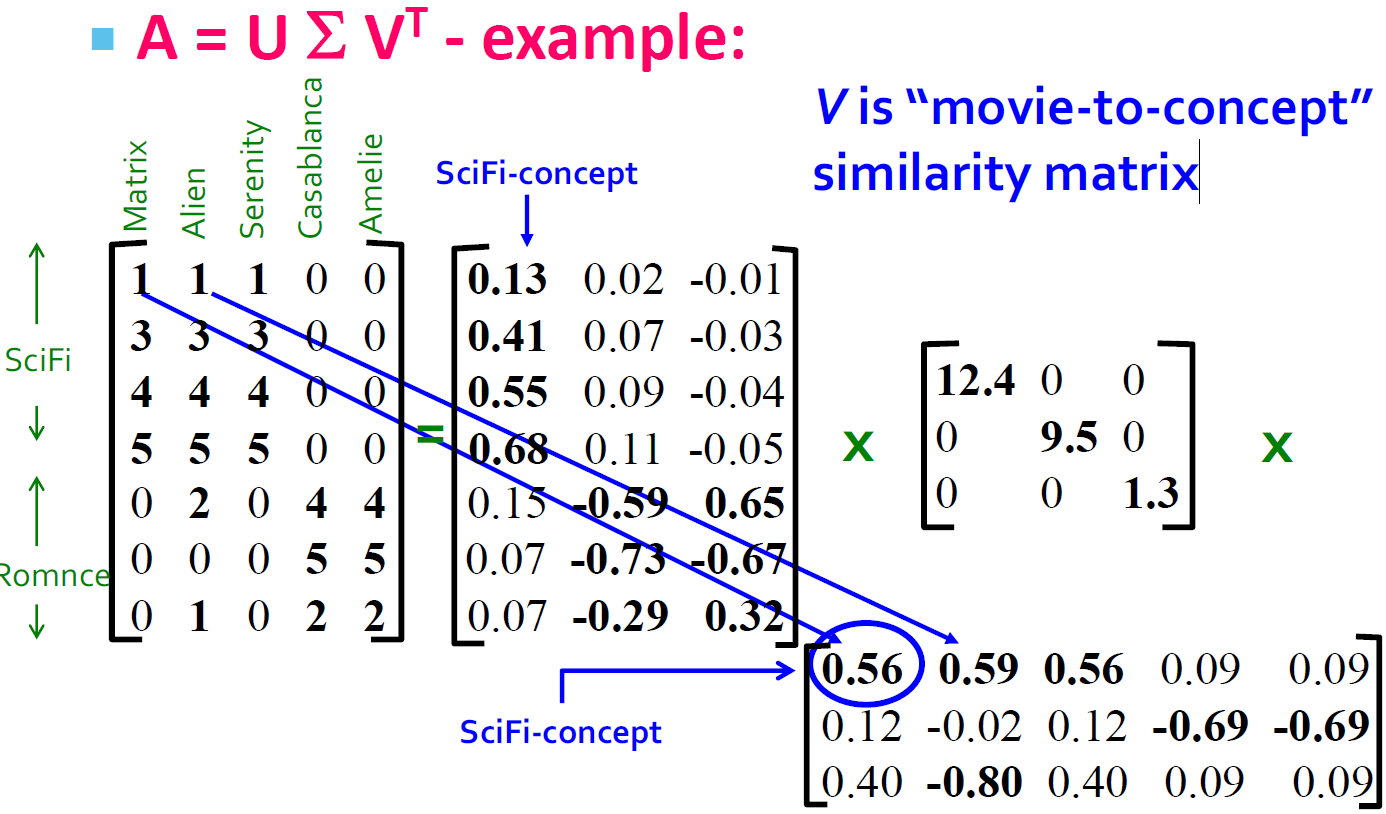
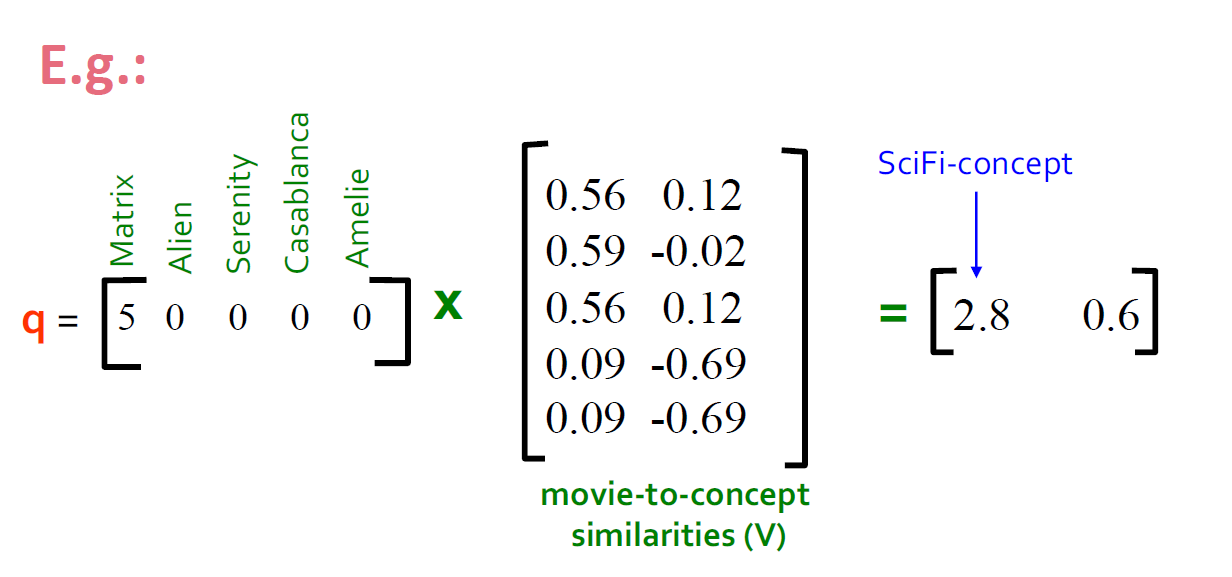
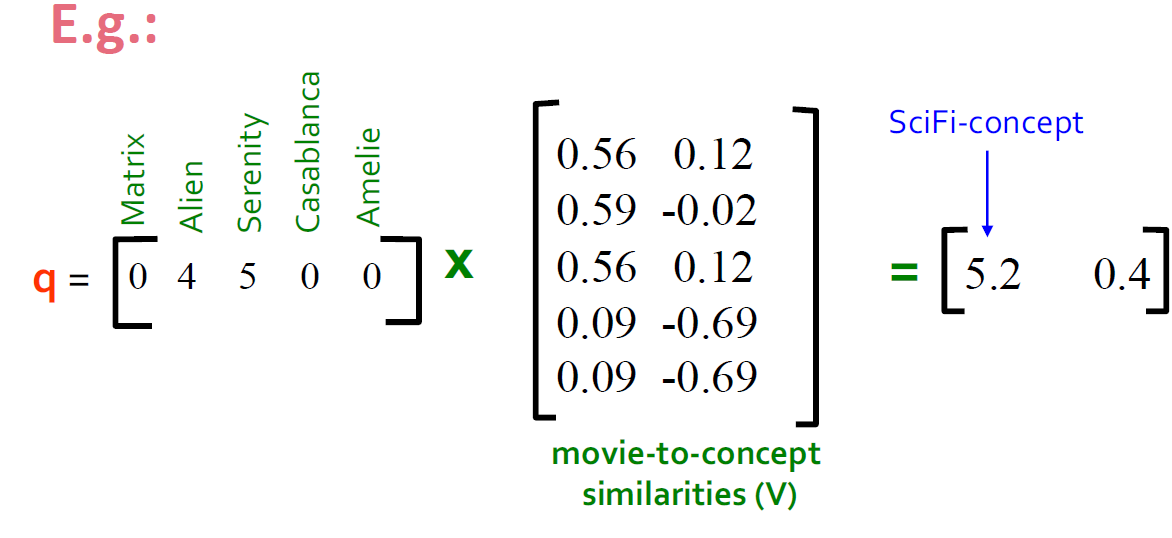
- U:“User to Concept”相似度矩阵
- 第一列:SciFi-concept
- 第二列:Romance-concept
- \(\Sigma\):
- 第一对角值:“strength” of the SciFi-concept
- 对角值:“strength” of each concept
- V:“movie-to-concept”相似度矩阵
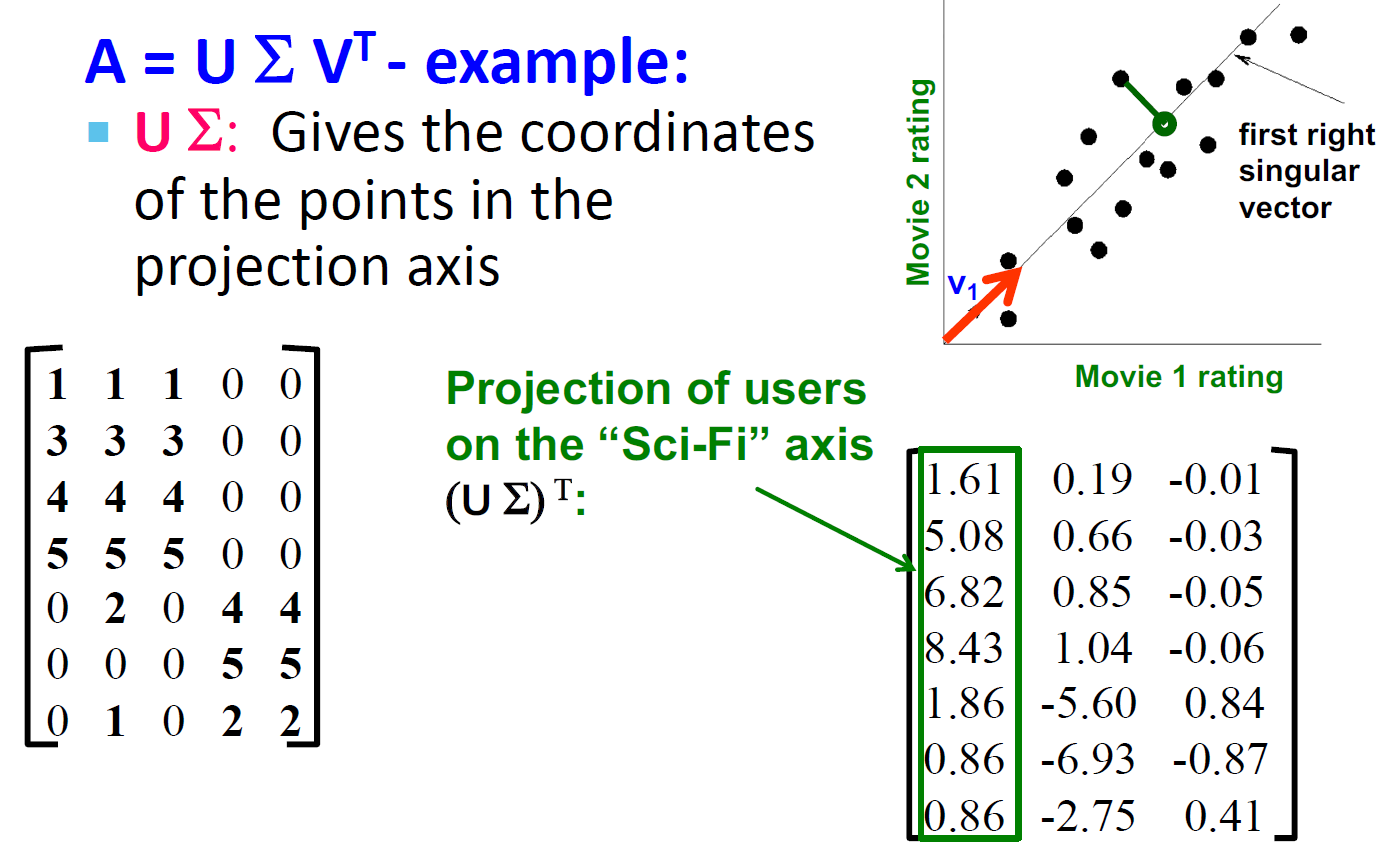
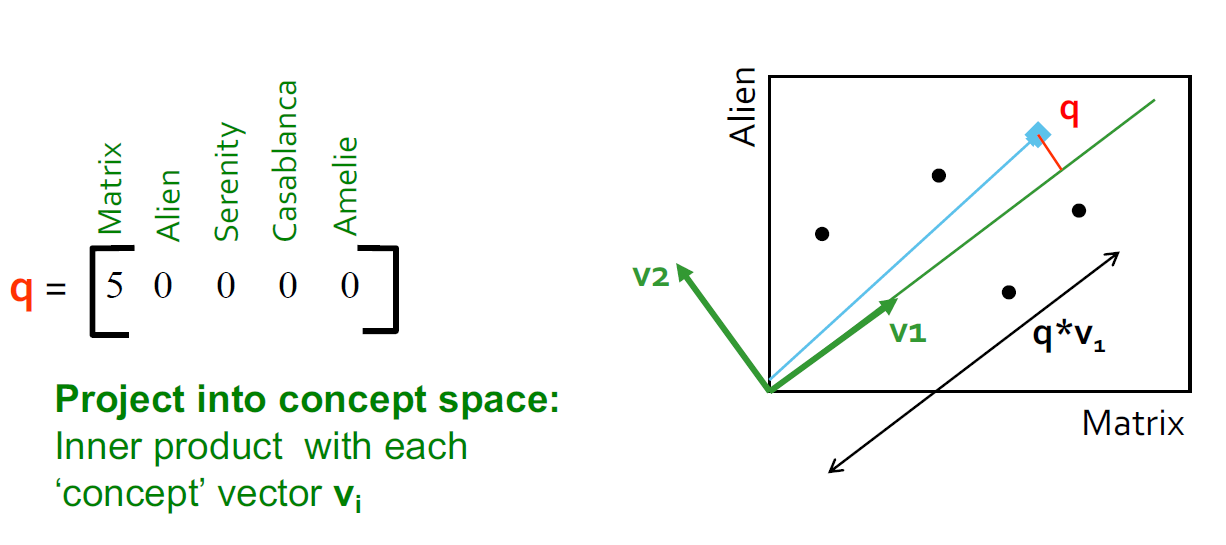
SVD 的向量理解
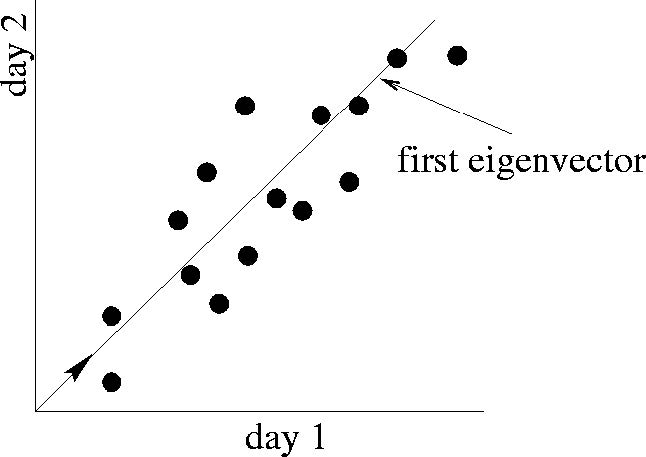
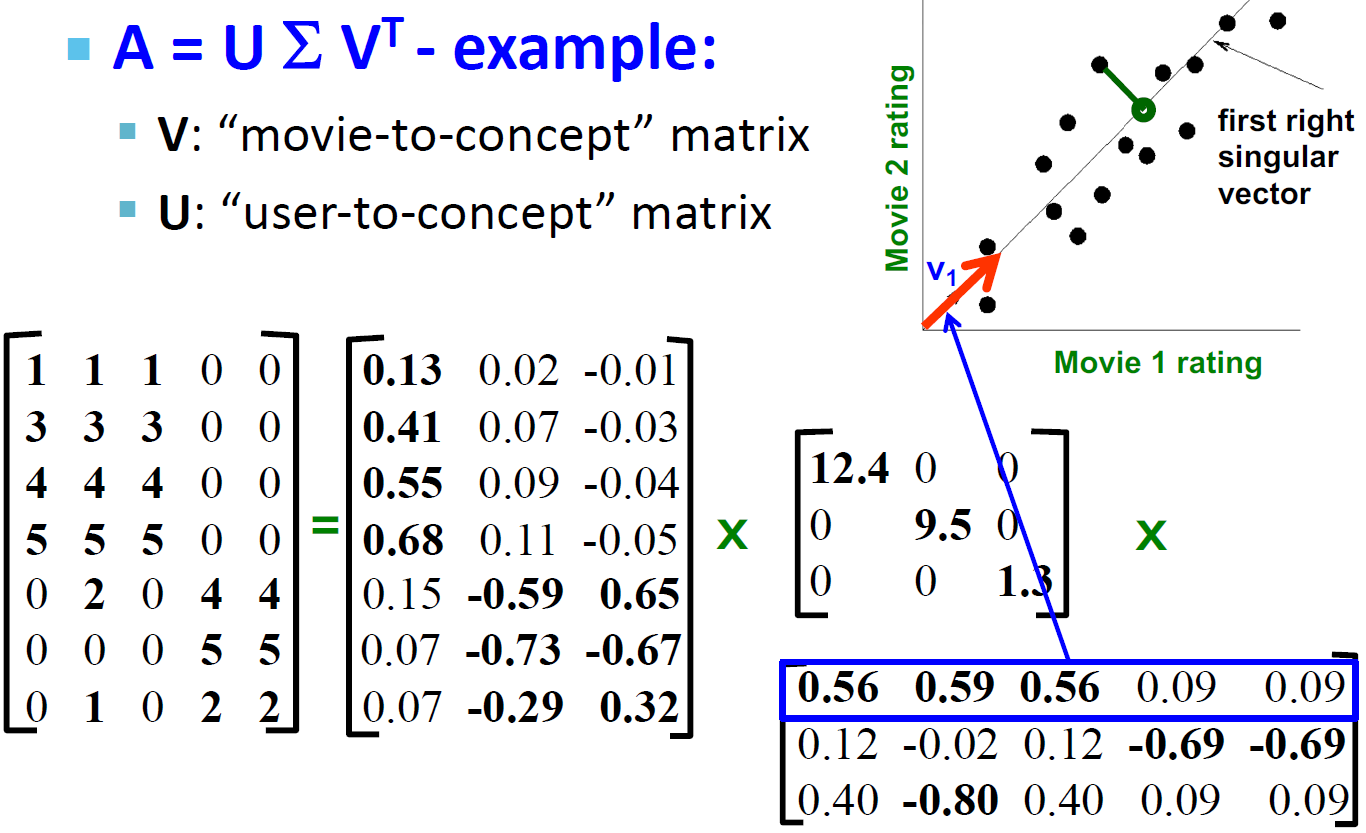
- 不使用二维(x, y)来描述一个点,而是使用一个点 z 来描述这个点。
- 点的位置是在向量 v1 上的
- 如何选择 v1:最小化 reconstruction errors(我们选择使用欧氏距离)
最小化 reconstruction errors
SVD 目标:最小化 reconstruction errors
\[ \sum\limits_{i = 1}\limits^{N}\sum\limits_{j = 1}\limits^D||x_{ij} - z_{ij}||^2 \to 0 \]
如何被认为是没有了,下降结束了?设置最小的奇异值为 0

- 得到 SVD 后的近似矩阵(将最小的奇异值设置为 0 和 U、V 中对应的行和列置为 0,重新做乘法得到新的矩阵)

SVD 向量理解例子:Users to Movies
SVD - 最低秩近似
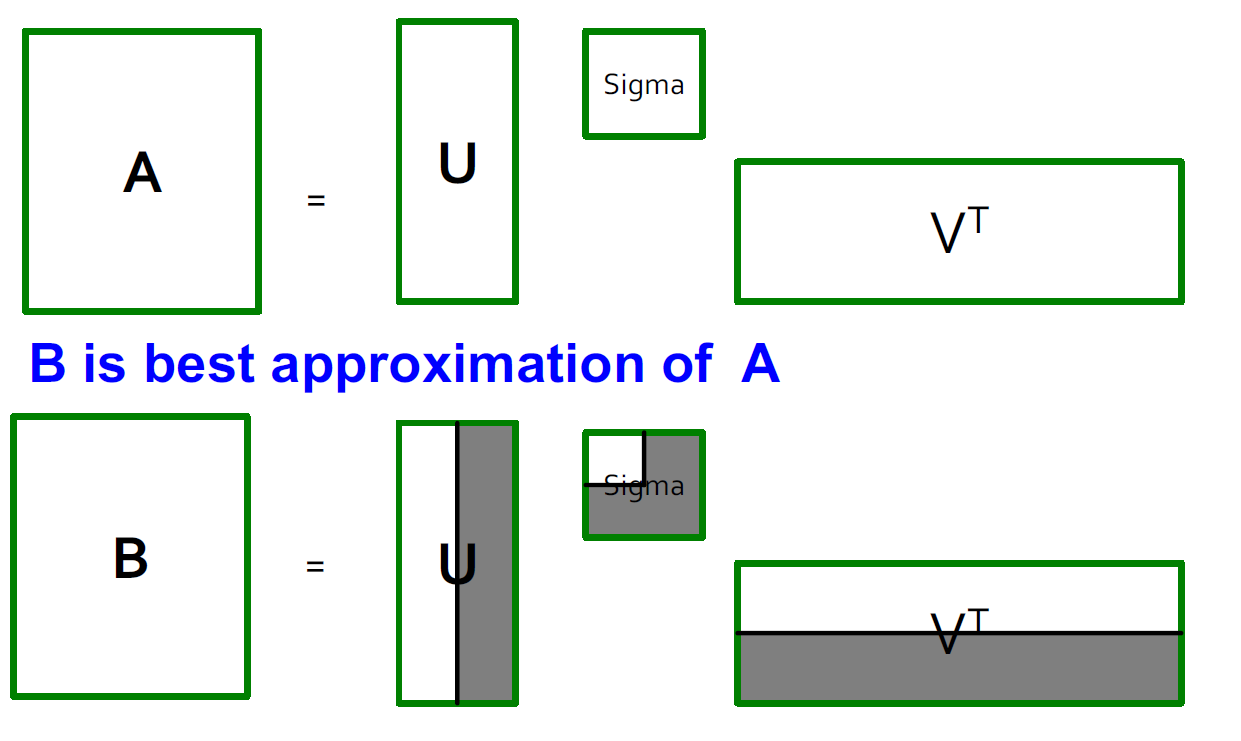
定理:如果 \(A = U\Sigma V^T\) 并且 \(B = U S V^T\),并且 S 是一个对角 r * r 的矩阵,并且 \(s_i = \delta_i(i = 1...k)\),并且其他的 \(s_i=0\),那么 B 是 A 的最合适的近似矩阵,并且 \(rank(B) = k\)
- 什么是最好?B 在\(rank(B) = k\)的时候是\(\min\limits_B||A-B||_F\)的解
- \(||A-B||_F = \sqrt{\sum\limits_{ij}(A_{ij} - B_{ij})^2}\)
引理
- \(||M||_F = \sum\limits_i(q_{ii})^2\) 当 M = P Q R 是 M 的 SVD 的时候
- \(U\Sigma V^T - USV^T = U(\Sigma - S)V^T\)
引理的证明
\[ \begin{array}{l} \|M\|=\sum\limits_i\sum\limits_j\left(m_{i j}\right)^{2}=\sum\limits_i \sum\limits_j\left(\sum\limits_k \sum\limits_lp_{i k} q_{kl} r_{lj}\right)^{2} \\ \|M\|=\sum\limits_i\sum\limits_j\sum\limits_k\sum\limits_l \sum\limits_n\sum\limits_m p_{ik} q_{kl} r_{lj} p_{in} q_{nm} r_{mj} \end{array} \]
- \(\sum\limits_ip_{ik}p_{in}\) 是 1,如果 k=n,不然为 0
- P 是列正交矩阵,R 是正交矩阵,Q 是对角矩阵
\[ \begin{array}{l} A = U \Sigma V^T, B = U S V^T \\ \\ \min\limits_{B, rank(B)=K}||A-B||_F \\ = \min ||\Sigma - S||_F = \min\limits_{s_i}\sum\limits_{i=1}\limits^r(\delta_i-s_i)^2 \end{array} \]
- 我们想要的是最小化 \(\min\limits_{s_i}\sum\limits_{i=1}^r(\theta_i-s_i)^2\)
- 解决方案就是令 \(s_i = \delta_i(i = 1...k)\) 并且其他 \(s_i=0\)
\[ \begin{array}{l} \min\limits_{s_i}\sum\limits_{i=1}\limits^k(\delta_i-s_i)^2 + \sum\limits_{i = k + 1}\limits^r\delta^2 \\ = \sum\limits_{i = k + 1}\limits^r\delta^2 \end{array} \]
定理的说明

为什么将 \(\delta_i\) 设置为 0 是正确的做法?
- 向量 \(u_i\) 和 \(v_i\) 是单位长度,所以 \(\delta_i\) 是用来调整他们的
- 所以让 \(\delta_i\) 成为 0 可以导致更少的损失
我们应该保持多少 \(\delta_s\),拇指原则:\(\sum\limits_i\delta_i^2\) 的和在 80%-90%,保证信息损失不太多
SVD 算法的复杂度
- 计算 SVD 的复杂度:\(\min(O(nm^2), O(n^2m))\)
- 但是如果我们只想知道奇异值或者前 k 个奇异值,或者矩阵是稀疏矩阵,那么复杂度会大大下降
SVD 和特征分解的关系
SVD 角度:\(A = U \Sigma V^T\)
特征分解的角度:\(A = X \Lambda X^T\)
- A 是对称的
- \(U,V,X\) 都是正交矩阵
- \(\Lambda,\Sigma\) 都是对角的
\[ \begin{array}{l} AA^T \\ = U\Sigma V^T (U\Sigma V^T)^T \\ = U\Sigma V^T (V\Sigma^TU^T) \\ = U\Sigma\Sigma^TU^T(X \Lambda^2 X^T )\\ \\ A^TA \\ = V(\Sigma^TU^T)(U\Sigma V^T) \\ = V\Sigma\Sigma^TV^T(X \Lambda^2 X^T ) \end{array} \]
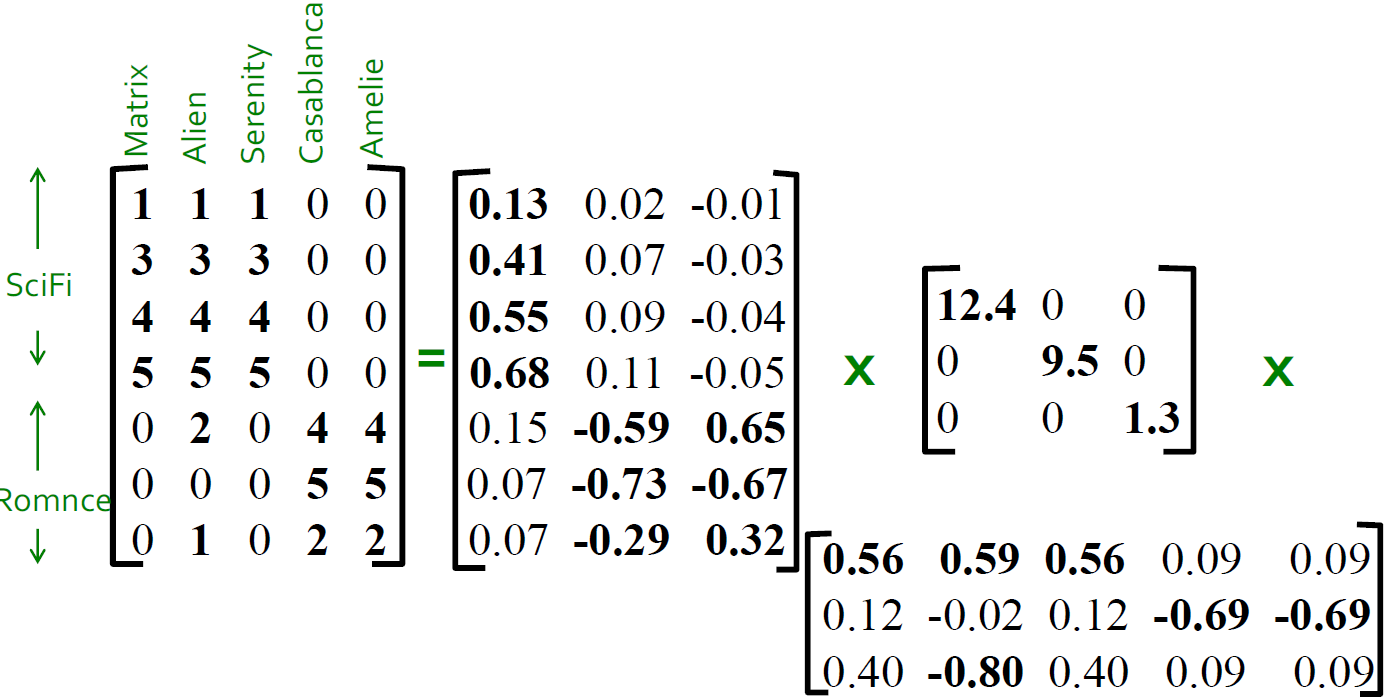
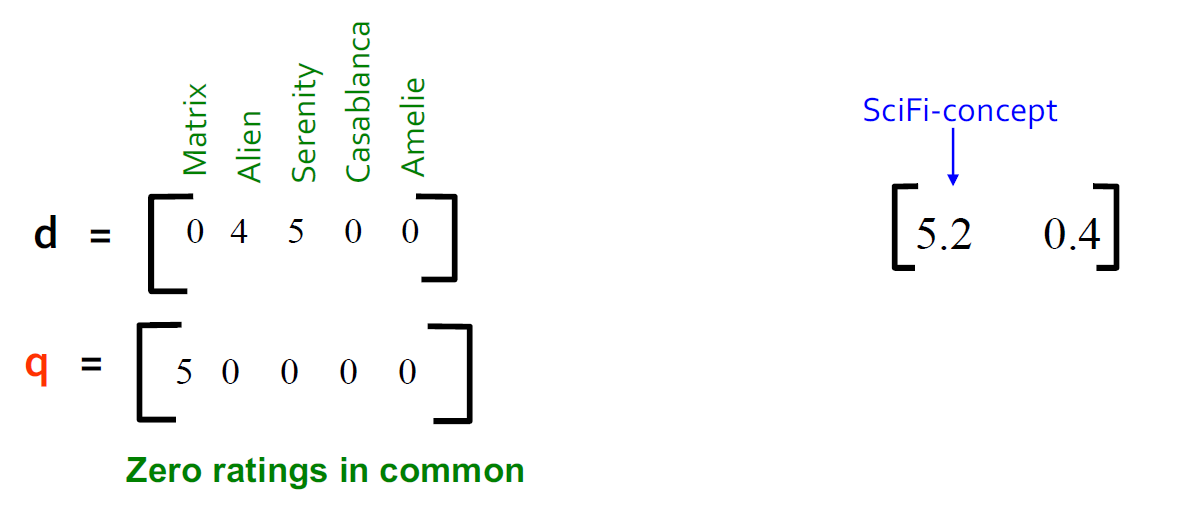
案例:如何查询
查找类似这个矩阵的用户:将查询映射到“概念空间”中-怎么做?
 |
 |
|---|
- user q:\(q_{concept} = q V\)
- user d:\(d_{concept} = d V\)
 |
 |
|---|
观察:被评级为“Alien”,“Serenity”的用户 d 与被评级为“Matrix”的用户 q 相似,尽管 d 和 q 的共同点为零!
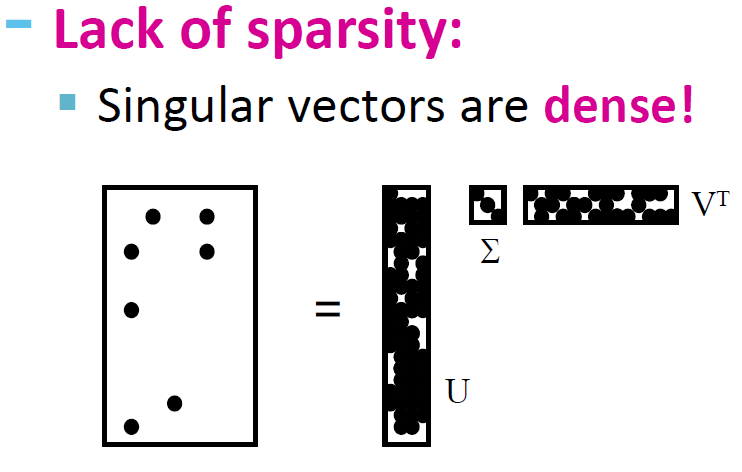
SVD 的效果
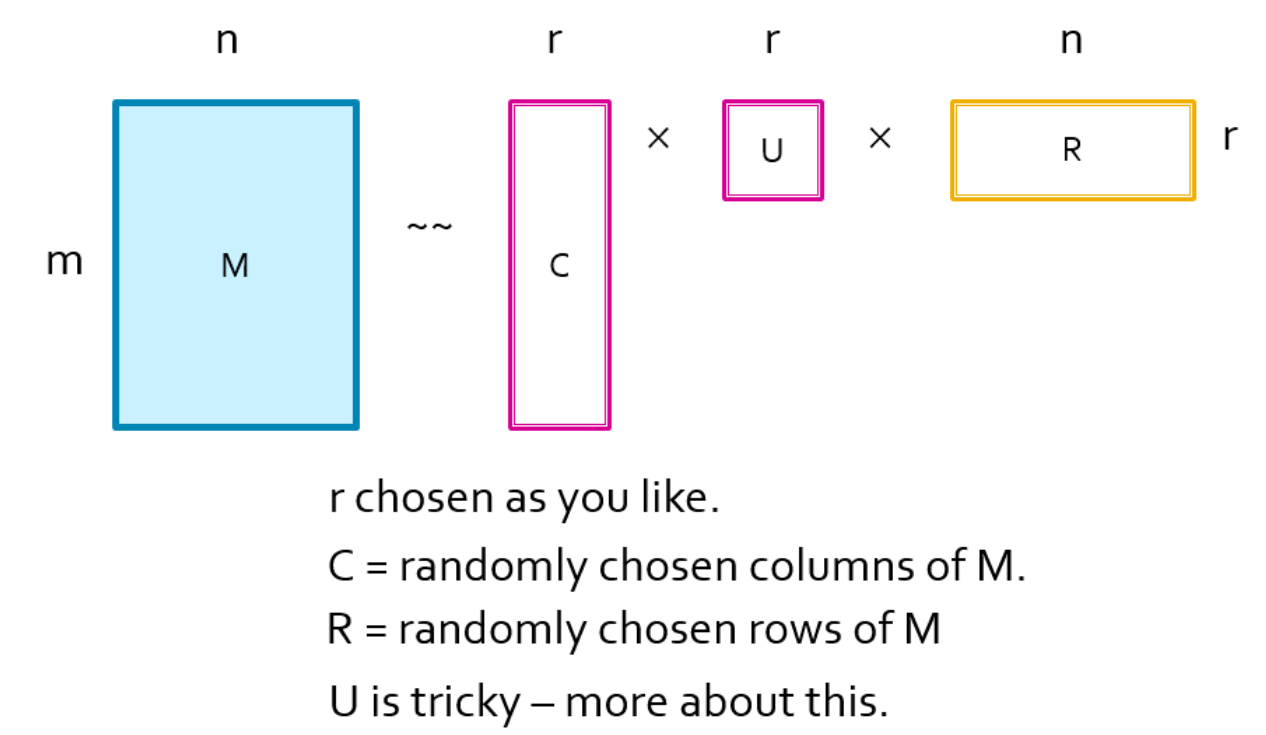
CUR 分解
目标:将矩阵 A 解释为 C,U,R,使得 \(||A - C*U*R||_F\) 最小
选择行和列的方式
- 尽管我们是随机的选择行和列,但是我们还是保留了对于重要的行和列的权重
- 行和列的权重计算:\(f=\sum\limits_{i,j}a_{ij}^2\)
- 我们按照概率 \(p_i = \sum\limits_{j}\frac{a_{ij}^2}{f}\) 选择行
- 我们按照概率 \(q_j = \sum\limits_{i}\frac{a_{ij}^2}{f}\)
- 归一化处理:将所有的元素都是除以 \(\sqrt{rq_j}\)(行)、\(\sqrt{rp_i}\)(列)
CUR 对列(行)进行取样
以列为例,行也是相似的
输入:矩阵 \(A \in R^{m * n}\),样例数 c
输出:\(C_d \in R^{m * c}\)
算法过程:
- 对于 \(\forall x \in [1, n],P(x) = \frac{\sum\limits_iA(i, x)^2}{\sum\limits_{i,j}A(i,j)^2}\)
- 对于 \(\forall i \in [1, c]\),以一列为例
- 选择 \(k \in [1, n]\) 满足分布 \(P(x)\)
- 计算 \(C_d(:,i) = \frac{A(:,k)}{\sqrt{cP(k)}} = \frac{A(:, k)}{\sqrt{c * \frac{\sum\limits_iA(i, k)^2}{\sum\limits_{i,j}A(i,j)^2}}}\)
请注意,这是一种随机算法,同一列可以多次采样
计算 U
U 是一个 \(r*r\) 的矩阵,所以是比较小的,并且如果他是高密度、难计算的也是可以的。
首先计算 W,我们让 W 是列 C 和行 R 的交集,并且计算出 W 的 SVD 表示为 \(W = X \Sigma Y^T\)
然后计算 \(\Sigma\) 的 Moore-Penorse inverse(伪逆矩阵):\(\Sigma\)
- \(\Sigma\) 是一个对角矩阵
- 他的 Moore-Penorse inverse 满足:
- \(\frac{1}{\sigma}\) 如果 \(\sigma \neq 0\)
- 0 如果 \(\sigma=0\)
然后:\(U = W^+ = Y(\Sigma^+)^2X^T\)
- 非零奇异值的倒数:\(\Sigma_{ii}^{+} = 1/\Sigma_{ii}\)
- \(W^+\) 是伪逆
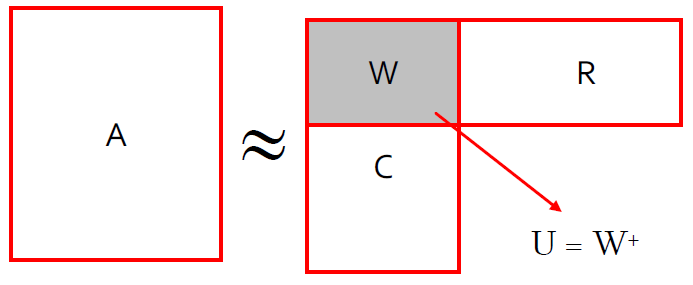
为什么伪逆是有效的
\[ \begin{matrix} W = X \Sigma Y \\ W^{-1} = X^{-1} * \Sigma^{-1} * Y^{-1} \\ \because X^{-1} = X^T, Y^{-1} = Y^T \\ \Sigma^{-1} = \frac{1}{\Sigma_{ii}} \\ \end{matrix} \]
- X、Y 正交矩阵,\(\Sigma\) 是对角矩阵
- 因此,如果 W 是非奇异矩阵,伪逆矩阵是真的逆矩阵
CUR 是可以被证明是 SVD 的一个很好近似

CUR 的优点和缺点
优点
- 很好计算:由于基向量是实际的列和行
- 稀疏矩阵:由于基向量是实际的列和行
缺点
- 重复的列和行:大量的列将被多次采样
如何避免重复
- 方案一:直接抛弃
- 方法二:用重复项的平方根缩放(乘)列/行
SVD 和 CUR
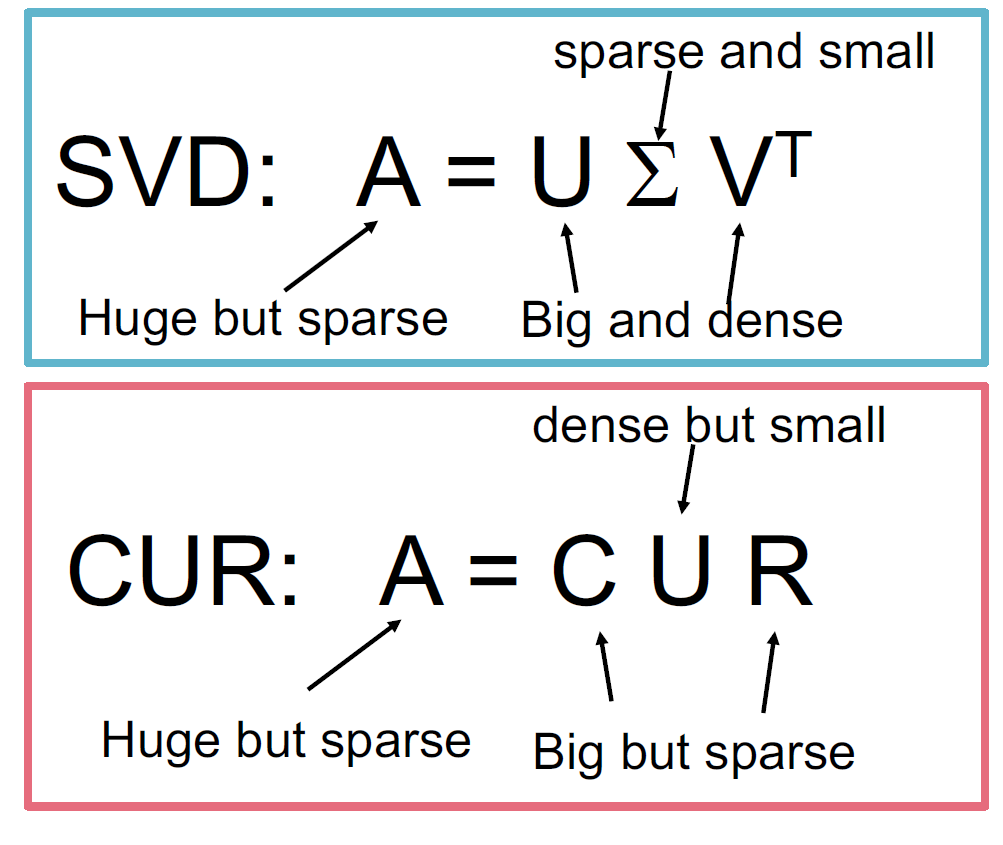
简单的实验
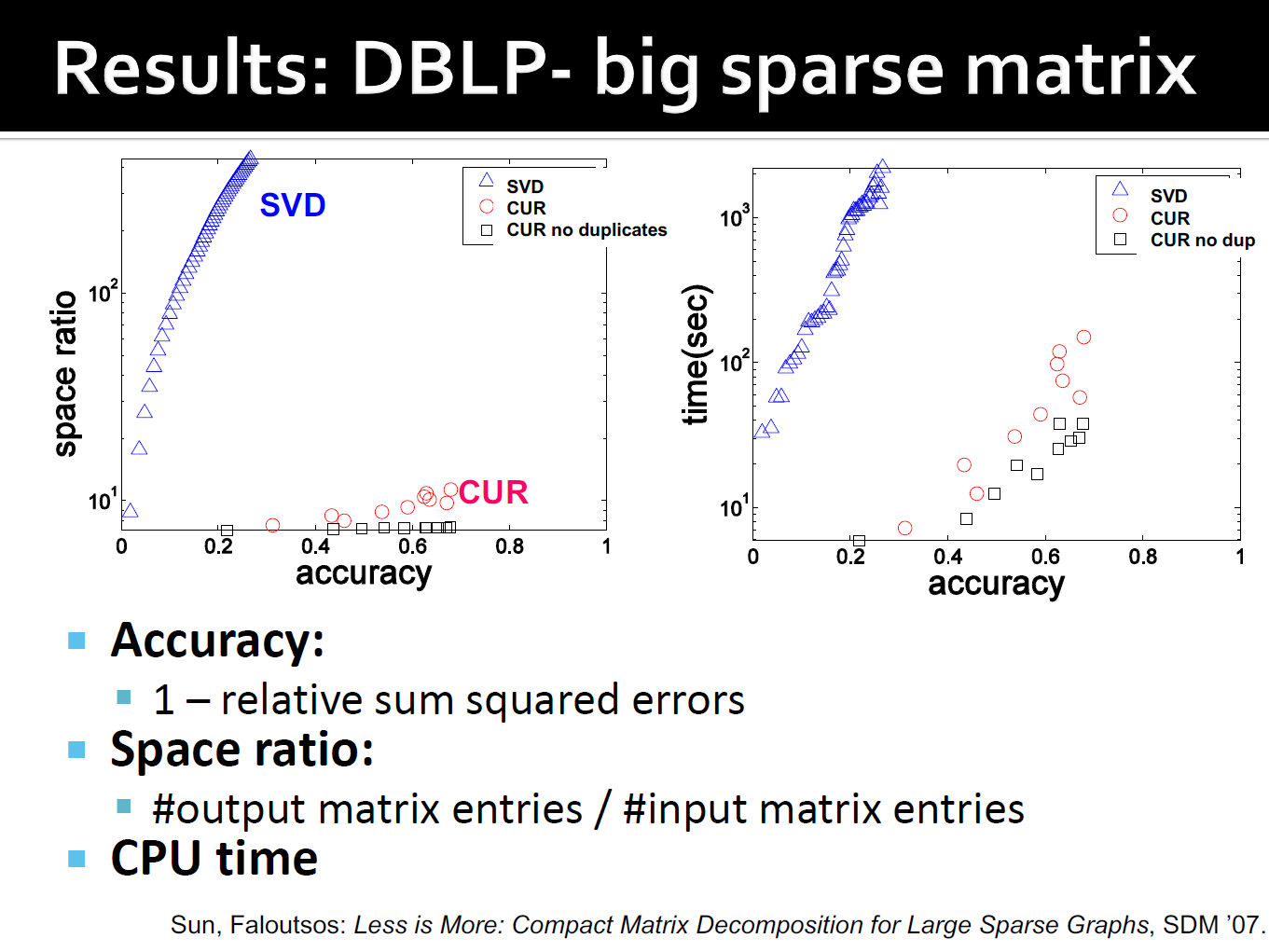
DBLP bibliographic data
- Author-to-conference 的大稀疏矩阵
- \(A_{ij}\):作者 i 在会议 j 上发表的论文数量
- 428k 个作者(列),3659 会议(行)
- 非常稀疏
DBLP 的结果
线性假设
SVD 只能用于线性投影:低维线性投影,保持欧式距离
非线性方法:Isomap
- 数据位于一个低维的非线性曲线
- 使用距离度量对应的形状

