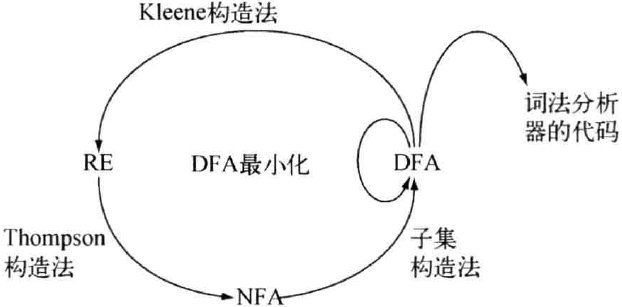
Thompson 构造法
作用:将正则表达式转化为 NFA
原理:按结构归纳。
给定字母表 \(\Sigma\),\(\Sigma\) 上的正则表达式由且仅由以下规则定义:
- \(\epsilon\) 是正则表达式
- \(\forall a \in \Sigma\), \(a\) 是正则表达式
- 如果 \(s\) 是正则表达式,则 \((s)\) 是正则表达式
- 如果 \(s\) 与 \(t\) 是正则表达式,则 \(s|t, st, s*\) 也是正则表达式
| 规则 | 设计 |
|---|---|
| \(\epsilon\) 是正则表达式 |  |
| \(\forall a \in \Sigma\), \(a\) 是正则表达式 |  |
| 如果 \(s\) 与 \(t\) 是正则表达式,则 \(s|t\) 是正则表达式 | 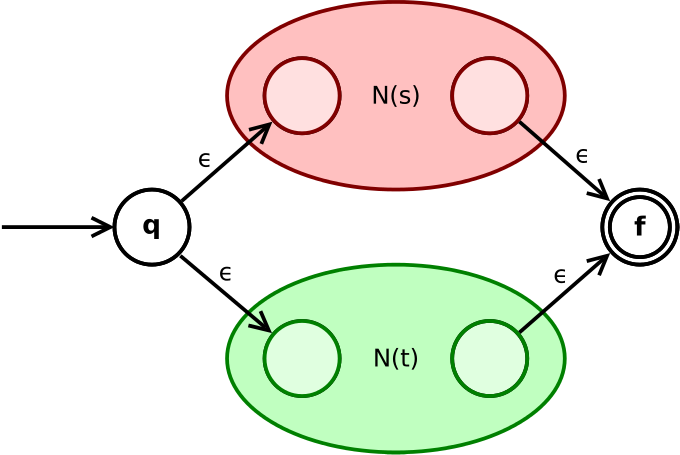 |
| 如果 \(s\) 与 \(t\) 是正则表达式,则 \(st\) 是正则表达式 | 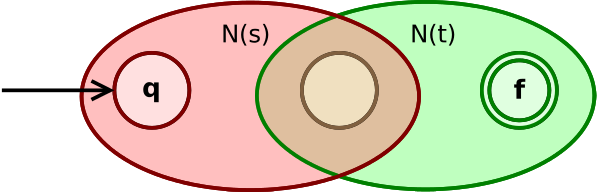 |
| 如果 \(s\) 与 \(t\) 是正则表达式,则 \(s*\) 是正则表达式 | 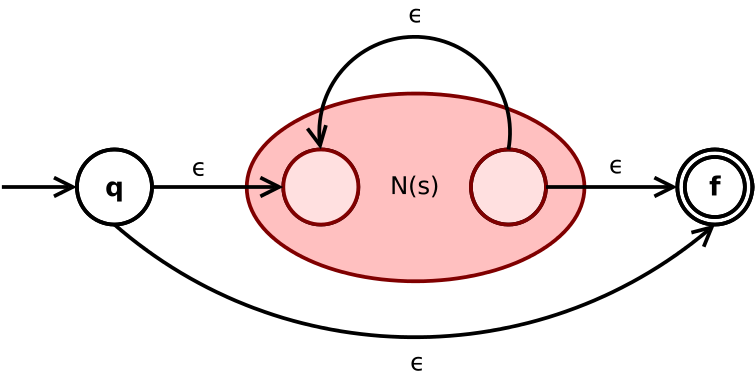 |
子集构造法
作用:将 NFA 转化成 DFA
原理:
- 对于给定的 NFA,确定其开始状态。如果有多个开始状态,则将它们作为新 DFA 的一个开始状态。
- 通过在 NFA 中执行 \(\epsilon-closure\) 操作,找到开始状态所能到达的所有状态。这些状态构成了 DFA 中的第一个状态。
- 对于 DFA 中的每个状态,找到从该状态通过每个输入符号可以到达的所有 NFA 状态。将这些 NFA 状态通过 \(\epsilon-closure\) 操作合并为一个新的 DFA 状态。
- 重复步骤3,直到所有新的 DFA 状态都已经找到。
- 对于 DFA 中的每个状态,标记它是否包含任何 NFA 接受状态。如果是,则该 DFA 状态也是接受状态。
- 构造完整的 DFA 转换表,其中每个输入符号都有一个转换函数,它指示当前状态下接受输入符号后进入的下一个状态。
- 最终的 DFA 状态集合就是转换后的 DFA。
初始 NFA
stateDiagram-v2
classDef endState stroke-width:3px
direction LR
[*] --> 0 : start
0 --> 1 : ϵ
1 --> 2 : ϵ
1 --> 3 : ϵ
2 --> 4 : 1
3 --> 5 : 0
5 --> 6 : 1
4 --> 7 : ϵ
6 --> 7 : ϵ
7 --> 1 : ϵ
7 --> 8 : ϵ
0 --> 8 : ϵ
8 --> 9 : ϵ
9 --> 10 : 0
10 --> 9 : ϵ
10 --> 11:::endState : ϵ
9 --> 11 : ϵ
计算过程
| NFA 状态集合 | DFA 状态 | 0 | 1 |
|---|---|---|---|
| 0, 1, 2, 3, 8, 9, 11 | A | B | C |
| 5, 9, 10, 11 | B | D | E |
| 1, 2, 3, 4, 7, 8, 9, 11 | C | B | C |
| 9, 10, 11 | D | D | \(\varnothing\) |
| 1, 2, 3, 6, 7, 8, 9, 11 | E | B | C |
转化后的 DFA
stateDiagram-v2
direction LR
classDef endState stroke-width:3px
[*] --> A : start
A:::endState --> C : 1
A --> B:::endState : 0
C:::endState --> B : 0
C --> C : 1
B --> E:::endState : 1
E --> B : 0
E --> C : 1
B --> D:::endState : 0
D --> D : 0
DFA 最小化算法
作用:将得到的 DFA 转化成最小的等价 DFA
原理:合并等价状态。
定义:所有后续状态都相同的状态是不可区分状态,即等价状态。
在转化后的 DFA 中,A、C、E 三个状态的后续状态完全相同,可以合并。
最小化的 DFA
stateDiagram-v2
direction LR
classDef endState stroke-width:3px
[*] --> a : start
a:::endState --> b:::endState : 0
b --> a : 1
a --> a : 1
b --> c:::endState : 0
c --> c : 0

