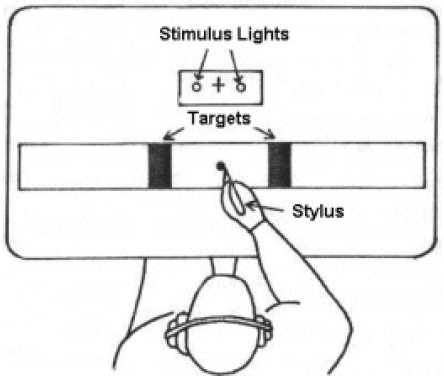
背景
汽车上的刹车踏板和油门踏板相距很近,且刹车踏板要比油门踏板大很多:
- 经验告诉我们,可达到以最快的速度准确制动的目的
- 但是,依据的原理是什么呢?
设计学科通常借助模型生成新的想法并对其测试:如建筑学领域,有重量分布模型、空气环流模型、流体力学模型和光学模型等
交互设计领域:
- 计算用户完成任务的时间:KLM
- 描述交互过程中系统状态的变化:状态转移网
- 探讨任务的执行方法等:GOMS
预测模型
能够预测用户的执行情况,但不需要对用户做实际测试
特别适合于无法进行用户测试的情形。
举例:为改进对员工使用计算机的支持,设计了许多可行方案。如何判断那一种方法更有效?
不同模型关注用户执行的不同方面:
- GOMS:击键层次模型 KLM
- Fitts 定律
GOMS 模型
最著名的预测模型,1983 年由 Card, Morgan 和 Newell 提出。
基于人类处理机模型,泛指整个 GOMS 模型体系,是关于人类如何执行认知—动作型任务以及如何与系统交互的理论模型。
- 采用“分而治之”的思想,将一个任务进行多层次的细化
- 把每个操作的时间相加就可以得到一项任务的时间:操作指用户的目光从屏幕的一处移到另一处、识别出某个图标、手移到鼠标上
GOMS 全称
- Goal-目标:用户要达到什么目的
- Operator-操作:任务执行的底层行为,不能分解:为达到目标而使用的认知过程和物理行为。如点击鼠标
- Method-方法:如何完成目标的过程,即对应目标的子目标序列和所需操作。如移动鼠标,输入关键字,点击 Go 按钮
- Selection-选择规则:确定当有多种方法时选择和方法。GOMS 认为方法的选择不是随机的
举例
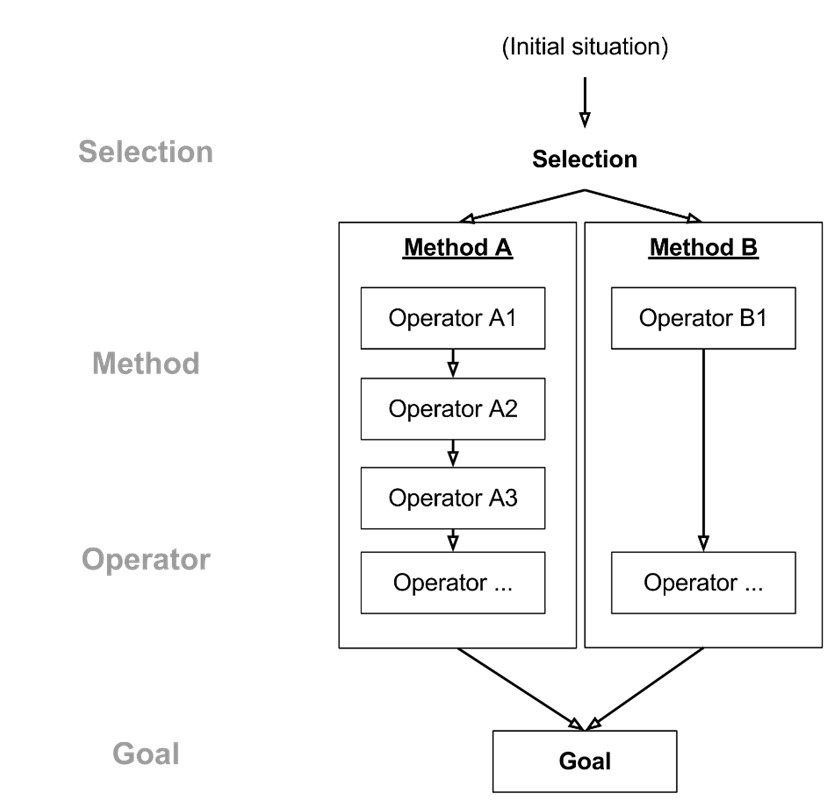
使用 GOMS 模型描述在 Word 中删除文本的过程
- 目标:删除 Word 中的文本
- 方法 1:使用菜单删除文本
- 步骤 1:思考,需要选定待删除的文本
- 步骤 2:思考,应使用“剪裁”命令
- 步骤 3:思考,“剪裁”命令在“编辑”菜单中
- 步骤 4:选定待删除文本,执行“剪裁”命令
- 步骤 5:达到目标,返回
GOMS 方法步骤
- 选出最高层的用户目标
- 写出具体的完成目标的方法:即激活子目标
- 写出子目标的方法:递归过程,一直分解到最底层操作时停止
- 子目标的关系:
- 顺序关系
- 选择关系:以 select:引导
GOMS 模型分析
优点:
- 能够容易地对不同的界面或系统进行比较分析
- 美国电话公司 NYNEX:利用 GOMS 分析一套即将被采用的新的计算机系统的应用效果不理想,放弃了使用新系统,为公司节约了数百万的资金。
局限性:
- 假设用户完全按一种正确的方式进行人机交互,没有清楚地描述错误处理的过程
- 只针对那些不犯任何错误的专家用户
- 任务之间的关系描述过于简单
- 忽略了用户间的个体差异
KLM 击键层次模型
Card 等 1983。对用户执行情况进行量化预测:仅涉及任务性能的一个方面:时间
用途:
- 预测无错误情况下专家用户在下列输入前提下完成任务的时间
- 便于比较不同系统
- 确定何种方案能最有效地支持特定任务
使用
执行时间预测方法:
- 列出操作次序,累加每一项操作的预计时间
- \(T_\text{execute}=T_K+T_P+T_H+T_D+T_M+T_R\)
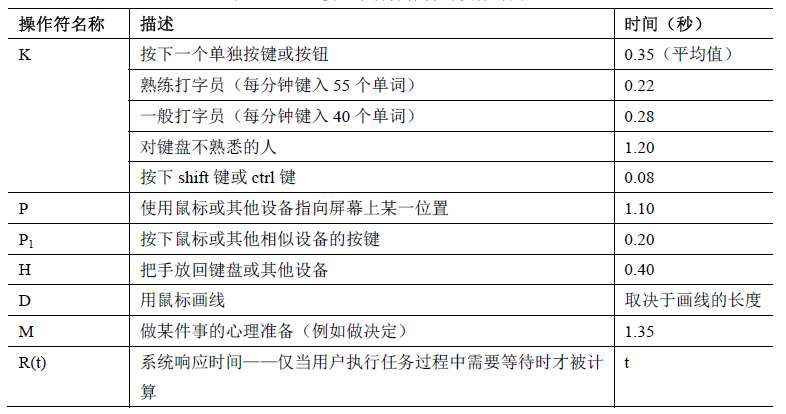
举例:
- DOS 环境下执行“ipconfig”命令:
M K[i] K[p] K[c] K[o] K[n] K[f] K[i] K[g] K[回车]- 简略表达版本:
M9K[ipconfig 回车] - \(T_\text{execute}=1.35 + 9 × 0.28 = 3.87\text{s}\)
- 菜单选择(不一定对,点击鼠标应该用 P1 而不是 K)
H[鼠标]MP[网络连接图标]K[右键]P[修复]K[左键]- \(T_\text{execute}=0.40+1.35+2P+2K=4.35s\)
编码方法
放置 M 操作符的启发规则
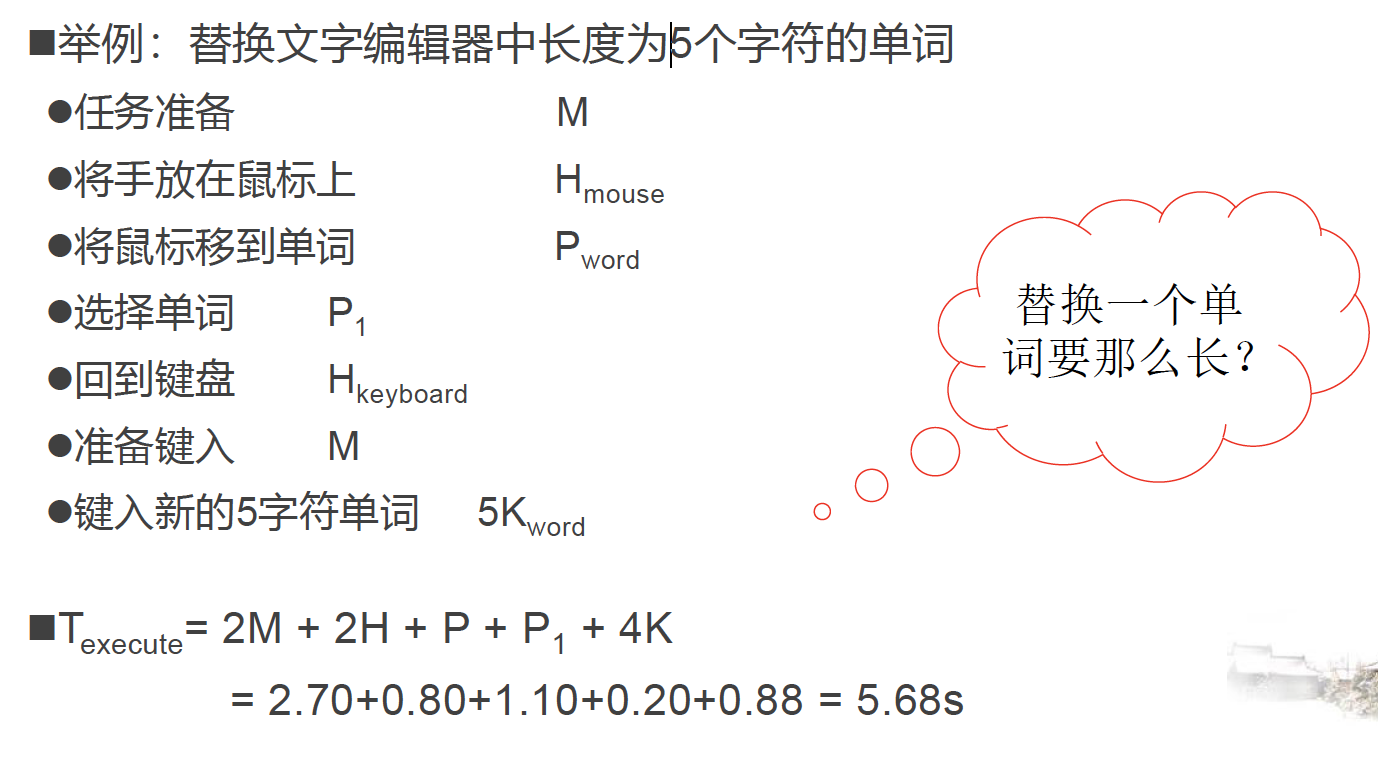
问题:如何确定是否需要在具体操作之前引入一个思维过程呢?
答案:

- 在每一步需要访问长时记忆区的操作前放置一个 M
- 在所有 K 和 P 之前放置 M:K \(\to\) MK; P \(\to\) MP
- 删除键入单词或字符串之间的 M:\(MKMKMK \to MKKK\)
- 删除复合操作之间的 M (如, 选中 P 和点击 P1):\(MPMP_1 \to MPP_1\)
KLM 分析
建模可以给出执行标准任务的时间
但没有考虑下面的问题:
- 错误
- 学习性
- 功能性
- 回忆
- 专注程度
- 疲劳
- 可接受性
Fitts 定律
Fitts,1954。用户访问屏幕组件的时间对于系统的使用效率是至关重要的。哪些特性会影响访问效率呢?
- 能够预测使用某种定位设备指向某个目标的时间
- 人机交互中,根据目标大小及至目标的距离,计算指向该目标的时间:可指导设计人员设计按钮的位置、大小和密集程度
- 对图形用户界面设计有明显的意义
- “最健壮并被广泛采用的人类运动模型之一”
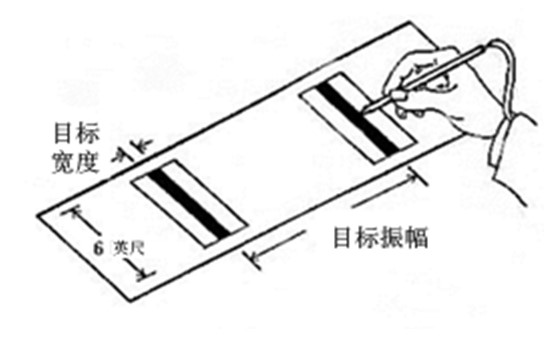
“轮流轻拍”实验
- 记录拍中和失误的情况
- 指令:尽可能准确而不是快速的轮流轻拍两个薄板
- 以实验数据为依据,得到困难指数如下
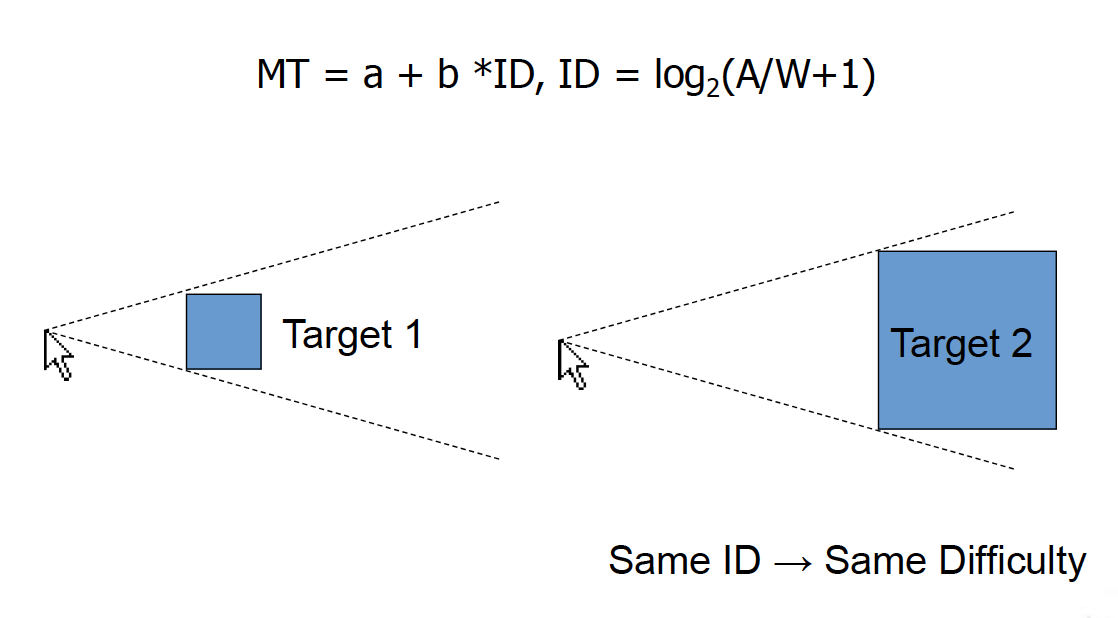
\[ ID = \log_2{\frac{2A}{W}} \]
概述
Fitts 定律描述了人类运动系统的信息量
信息论中的 Shannon 定理
\[ C = B \log_2(\frac{S}{N}+1) \]
C 是有效信息量(比特),B 是通道带宽,S 是信号能量,N 是噪声
Fitts 定律:S 映射为运动距离或振幅(A),N 映射为目标的宽度(W)
三个部分
- 困难指数 ID (Index of Difficulty) = \(\log_2{\frac{2A}{W}}\)
- 对任务困难程度的量化
- 与宽度和距离有关
- 运动时间 MT (Movement Time) = a + b*ID (secs):在 ID 基础上将完成任务的时间量化
- 性能指数 IP (Index of Performance) = ID/MT (bits/sec)
- 基于 MT 和 ID 的关系
- 也称吞吐量
- MacKenzie 改写为
- ID = log2(2A /W )
- ID = log2(A /W +1)
- 更好地符合观察数据
- 精确地模拟了支撑 Fitts 定律的信息论:C = B log2(S/N+1)
- 计算出的任务困难指数总是整数
- 平均时间 MT
- \(MT = a+b \log_2{(\frac{A}{W} + 1)}\)
- 常数 a 和 b 来自实验数据的线性回归
说明
- 如果 MT 的计算单位是秒,则 a 的测量单位是秒,b 的测量单位是秒/比特(ID 的测量单位是比特)
- 系数 a(截距)和 b(斜率)由经验数据确定,且与设备相关
- 对于一般性计算,可使用 a=50,b=150(单位是毫秒)
- A 和 W 在距离测量单位上必须一致,但是不需要说明使用的具体单位
Fitts' Law
Fitts 定律建议
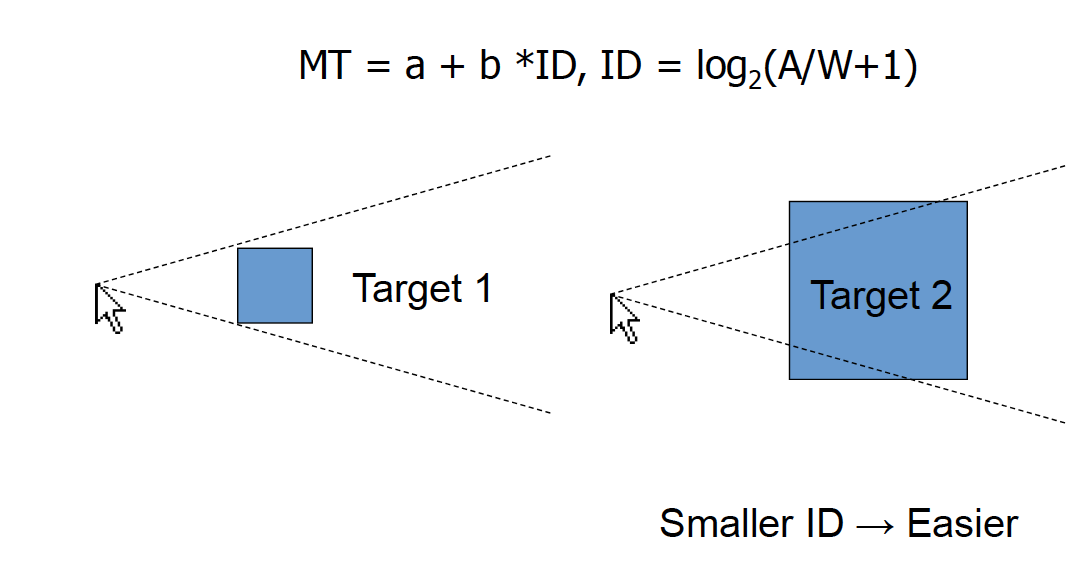
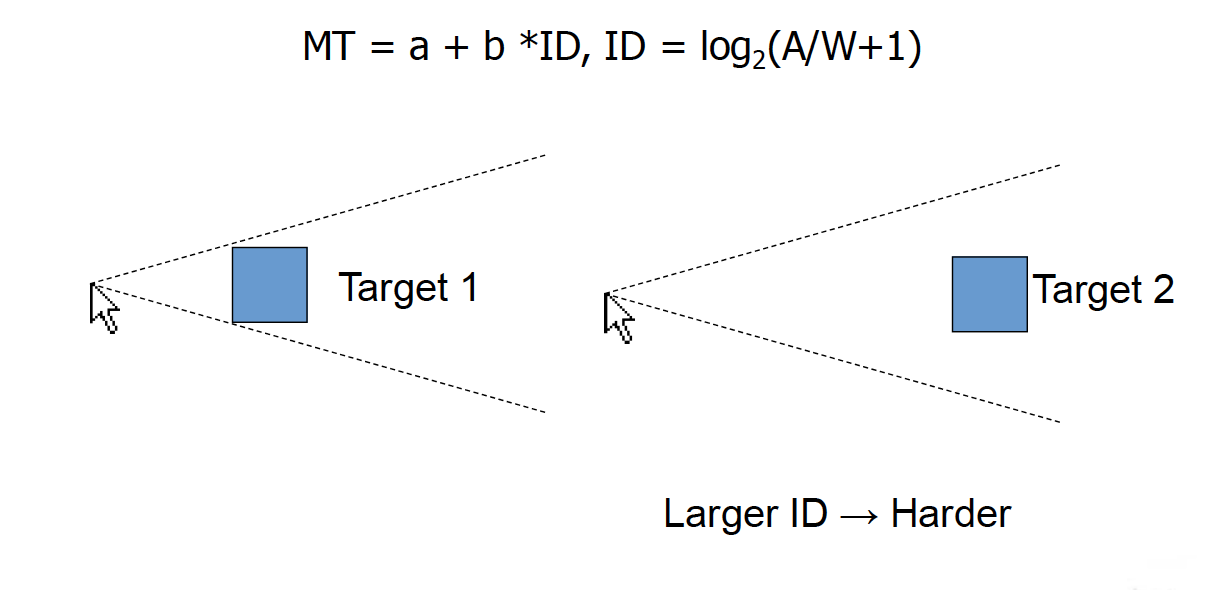
- 大目标、小距离具有优势:对选择任务而言,其移动时间随到目标距离的增加而增加,随目标的大小减小而增加
- 屏幕元素应该尽可能多的占据屏幕空间
- 最好的像素是光标所处的像素
- 屏幕元素应尽可能利用屏幕边缘的优势
- 大菜单,如饼型菜单,比其他类型的菜单使用简单
\[ ID = \log_2{(\frac{A}{W} + 1)} \]
Fitts 定律应用
首先被 Card 等人应用在 HCI 领域:
- 鼠标的定位时间和错误率都优于其他设备
- 鼠标速率接近最快速率
- 使用鼠标完成运动任务比使用其他设备更加协调,这在交互设计中非常重要
- 策略一:缩短当前位置到目标区域的距离,如右键菜单技术
- 策略二:增大目标大小以缩短定位时间:Windows 操作系统和 Macintosh 操作系统中的应用程序菜单区域位置的设计
应用实例
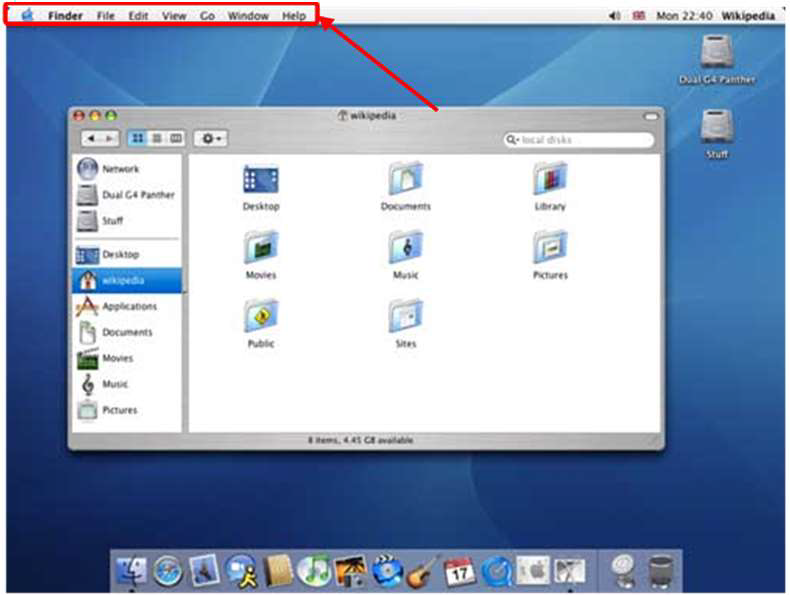
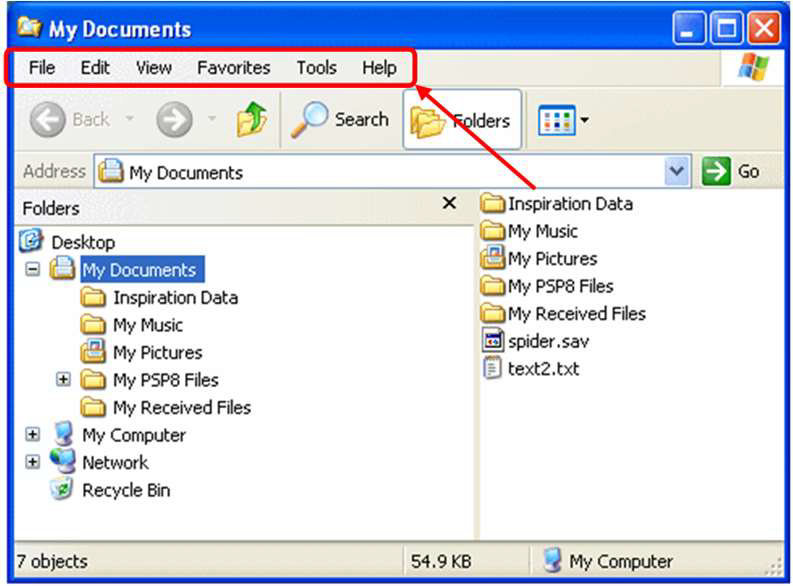
Mac OS 和 Windows XP 的比较(苹果专利)
- Mac OS 的菜单是沿着屏幕边缘排列的
- Windows OS 的菜单位于标题栏下面
Jeff Raskin
- 用户往往在距离屏幕边缘 50 毫米处停下来:50 毫米作为 Mac OS 的菜单宽度
- 对于 Mac OS:MT = 50 + 150 log2(80/50+1) = 256 ms
- 对于 Windows OS:MT = 50 + 150 log2(80/5+1) = 663 ms
Mac OS “dock”
工具栏组件大小可以动态改变:
- 为用户提供了一个放大的目标区域
- 可显示更多图标
- 新版 Mac 操作系统中都实现了扩展工具栏

思考:该工具栏存在何种优缺点?
Fitts 定律测验一
- 微软工具栏允许用户在图标下方显示图标标签
- 列举一条原因,解释为什么显示标签后工具条的访问速度更快?
- 假设用户明确每个图标的用途
- 参考答案
- 加大了图标面积。根据 Fitts 定律,在其他条件不变的情况下,目标越大,访问越快
- 改变了工具栏图标过于拥挤的情况
Fitts 定律测验二
- 图形应用工具中的调色板如左图
- 每个图标的大小为 16X16 像素
- 以 2 列 X8 行排列在屏幕左侧
- 问题:不改变图标大小,且保持图标阵列位于屏幕左侧,采取何种方式可减少访问每个图标所需的时间?

