EagleBear2002 的博客

这里必须根绝一切犹豫，这里任何怯懦都无济于事

arXiv'25-Using Read Promotion and Mixed Isolation Levels for Performant

发表于 更新于 分类于 ，
本文字数： 6.3k 阅读时长 ≈ 6 分钟

$$
\def\wr{\mathsf{\textcolor{teal}{wr}}}
\def\ww{\mathsf{\textcolor{red}{ww}}}
\def\rw{\mathsf{\textcolor{blue}{rw}}}
\def\C{\mathsf{C}}
\def\A{\mathcal{A}}
\def\T{\mathcal{T}}
\def\P{\mathcal{P}}
\def\D{\mathrm{D}}
\def\RC{\mathrm{RC}}
\def\SI{\mathrm{SI}}
\def\SSI{\mathrm{SSI}}
$$

摘要

我们提出一种理论方法，能够为应用程序中的每个事务程序分配最低可行的隔离级别（在多隔离级别混合设置下），从而保证所有执行均可序列化，进而维护所有完整性约束（包括未显式声明的约束）。该理论扩展了先前针对完全已知事务的研究，以应对实际场景中事务由运行时参数化程序动态生成的挑战。基于此理论，我们提出一种优化方法——读提升与混合隔离级别分配（RePMILA），在确保执行可序列化的同时实现高吞吐量。该方法通过语义保持的代码修改（将部分读操作“提升”为无实际数据变更的写操作以获取排他锁），并结合隔离级别分配优化，探索性能最佳的实现方案。我们以 SmallBank 基准测试为例，展示了该方法在 PostgreSQL 上的性能表现：某些读提升策略的鲁棒分配方案，其吞吐量可与未修改程序在默认非鲁棒的“读已提交（Read Committed）”隔离级别下的性能相媲美，同时仍保证可序列化；相较于所有事务使用“可序列化快照隔离（SSI）”的方案，吞吐量可提升两倍。

作者：

  • Brecht Vandevoort, UHasselt, Data Science Institute, ACSL, Belgium
  • Alan Fekete, University of Sydney
  • Bas Ketsman, Vrije Universiteit Brussel, Belgium
  • Frank Neven, UHasselt, Data Science Institute, ACSL, Belgium
  • Stijn Vansummeren, UHasselt, Data Science Institute

Introduction

事务管理是数据库管理系统的核心能力之一。虽然研究仍在持续探索提高性能的方法，特别是利用新型硬件[9, 12, 18, 19, 24–26, 29–32, 35]，但是大多数应用软件运行在流行的平台上，这些平台的并发控制机制已经存在了几十年，且众所周知在事务冲突时会遇到瓶颈，导致可序列化事务在竞争激烈时表现不佳[37, 43]。基于许多应用程序在领域特定的原因下不需要完美的序列化，这些平台为应用程序员提供了隔离级别的选择。因此，程序员可以选择较弱的隔离级别，例如平台默认的 READ COMMITTED 级别[6]，以在适当时提高性能。然而，目前还没有一个成熟的方法来帮助程序员判断何时接受非序列化隔离级别是合理的。

Robustness of transactions to guarantee serializability

近年来，理论研究提供了算法，能够分析应用程序中的事务集合，并为每个事务在混合隔离级别设置下选择隔离级别，同时仍能保证应用程序的健壮性[41]。也就是说，应用程序的每一次执行都会是可序列化的，即使其中一些事务并未使用可序列化的隔离级别执行。这项任务被称为“分配问题”[20]，需要对平台使用的并发控制机制进行一定的特征化。特别是，使用传统共享锁和独占锁操作单版本数据的系统得出的结论，将与允许读取已被覆盖数据版本（因此不阻塞读取）的多版本系统得出的结论不同[20, 28]。

然而，当前用于解决分配问题的理论假设，所有事务在分配时是完全已知的，包括所有将要读取和写入的项。这在实际中并不现实：实际上，应用程序执行时的事务是通过运行时参数生成的，这些参数在分配之后才会提供。例如，一个学生注册系统可能会有一个程序将学生注册到特定的课程，而具体的学生ID和课程代码直到程序执行时才由最终用户提供。

Robustness of transaction templates

本文的一个关键技术进展是提出了一个算法，能够确定在一组模板中为每个模板分配的最低隔离级别，其中模板是一个抽象，旨在捕获基于某些变量确定其读写集的事务。该算法返回的分配保证在如 PostgreSQL 这类提供多版本并发控制机制的平台上是健壮的。也就是说，任何实例化这些模板的事务集的执行都会是可序列化的。

Optimization via read promotion and mixed-isolation level allocation

我们提出的分配算法能够找到一种方法，在保证事务执行可序列化的同时，提升应用程序的性能（即保持所有数据约束的完整性，包括那些数据库中未显式声明的数据约束），而不会比将每个事务都执行在可序列化级别下的性能更差。我们建议考虑通过“提升”某些读取操作[21]的方式来修改应用程序代码，这些操作会被视为身份更新，并设置独占锁。在每个提升选择下，我们使用我们的分配算法来确定最低的隔离级别。对于每个提升选择和确定的健壮分配，我们可以通过实验测量其性能；性能最优的提升选择将是应用程序应采用的编码方式。我们称这种优化方法为读取提升与混合隔离级别分配（RePMILA）。

我们用著名的 SmallBank 基准测试[3]来说明 RePMILA，并探索在不同工作负载参数下，在 PostgreSQL 上获得的性能。我们发现，一些提升选择的健壮分配，其吞吐量与所有事务都使用 READ COMMITTED 时的吞吐量相当，但不同于后者，这些健壮分配仍然保证了序列化执行。此外，健壮分配下的吞吐量可以是将所有事务在平台的可序列化隔离级别下运行时吞吐量的两倍。

Contributions

本文的贡献包括理论与实验结果，我们还为从业者提供了指导。在理论方面，我们提供了一种证明技术，能够展示多版本隔离级别分配对事务模板的健壮性，并提出了一种多项式时间算法，能够生成唯一的最低健壮分配。我们为 SmallBank 应用提供了实验演示，证明了一些提升选择能够实现接近默认非健壮分配的性能（远好于所有事务都使用可序列化隔离级别时的情况）。我们认为，在这种背景下，RePMILA 对从业者非常有用，因为它在保证序列化执行的同时提升了性能。

Organization

本文的其余部分结构如下：第二节展示了 RePMILA 如何应用于 SmallBank，介绍了每个程序如何抽象为模板，分配算法如何为这些模板确定隔离级别，如何生成不同的提升选择，以及为每个提升选择生成的分配；第三节展示了不同提升选择的实测性能，并与所有程序都在可序列化隔离级别下运行的基准情况进行对比，也与所有程序都在默认的 READ COMMITTED 隔离级别下运行的基准情况进行对比；第四节介绍了理论部分，并详细介绍了分配算法；第五节讨论了相关工作；第六节讨论了本文工作的影响与局限，并指出了未来的研究方向。

READ PROMOTION AND MIXED ISOLATION LEVEL ALLOCATION (REPMILA)

为了说明我们的方法，我们通过著名的 SmallBank 基准应用[3]来进行演示。虽然它不是一个真实的例子，但它具备足够的特性来展示如何识别一个高效且健壮的分配，并且它足够简单，适合用于会议论文中。

SmallBank benchmark

SmallBank[3]模式包含以下表：Account(Name, CustomerID)，Savings(CustomerID, Balance) 和 Checking(CustomerID, Balance)（关键属性下划线标出）。Account 表将客户名称与客户ID关联。其他表存储客户的储蓄账户和支票账户余额（通过其ID进行标识）。应用程序代码通过事务程序与数据库交互：

  • Balance(N) 返回客户名称为 N 的总余额（包括储蓄和支票账户余额）。
  • DepositChecking(N, V) 向客户 N 的支票账户存入金额 V（见图 1）。
  • TransactSavings(N, V) 向客户 N 的储蓄账户存入或提取金额 V。
  • Amalgamate(N1, N2) 将客户 N1 的所有资金转账到客户 N2。
  • 最后，WriteCheck(N, V) 向客户 N 的账户开具支票，若账户透支则扣款。

Transaction templates

我们通过事务模板来抽象事务程序，如图 2 所示。相应的 SQL 代码在附录 A.1 中提供。事务模板由一系列读取（R）、写入（W）和更新（U）操作组成，每个操作访问一个元组。例如，R [X : Account{N, C}] 表示对 Account 表中 Name 和 CustomerID 属性的元组 X 执行读取操作。为了节省空间，我们将属性名称缩写为首字母。集合 {N, C} 是读取操作的读取集。类似地，W 和 U 表示写入和更新操作，操作对象是特定关系中的元组。写入操作具有与之相关的写入集，而更新操作包含一个读取集和一个写入集，例如 U [Z : DepositChecking{C, B}{B}]，首先读取元组 Z 的 CustomerID 和 Balance，然后写入 Balance 属性。U 操作是原子更新，首先读取元组，然后再写入它。模板作为事务程序的抽象，表示无数可能的工作负载。例如，假设 x、y、z（及其带有引号的版本）是具体的数据库对象，作为变量 X、Y 和 Z 的解释。那么，不考虑属性集的情况下，{R [x] R [y] R [z] U [z], R [x'] R [y'] R [z'] U [z'] , R [x] U [z]} 就是与 SmallBank 模板一致的一个工作负载，它包含了两次 WriteCheck 的实例化和一次 DepositChecking 的实例化。需要注意的是，{R [x] R [y] R [z] U [z']} 是一个无效工作负载，因为在 WriteCheck 中，最后两个操作应该作用于相同的对象。

事务模板没有捕获程序中的所有约束，因此可能会过度估计在实际程序执行时可能发生的事务。例如，工作负载 {R [t] U [q], R [t] U [q']} 与 SmallBank 模板一致（两次 DepositChecking 的实例化），但在实际中无法发生，因为假设每个客户只能有一个支票账户。

Lowest robust allocation

我们感兴趣的是确定每个模板的最低隔离级别分配，以确保所有执行都将是可序列化的。我们将这种分配称为健壮分配。我们考虑 PostgreSQL 的隔离级别：Read Committed（RC）、Snapshot Isolation（SI）和 Serializable Snapshot Isolation（SSI），并按从低到高的顺序将它们排列：RC < SI < SSI，假设当隔离级别降低时，吞吐量增加。我们在第 4 节中描述的分配算法发现，将 DepositChecking 映射到 RC，将所有其他模板映射到 SSI 是健壮的，并且从优化的角度来看是最优的，因为没有任何隔离级别可以降低而不破坏健壮性。

Read promotion choices

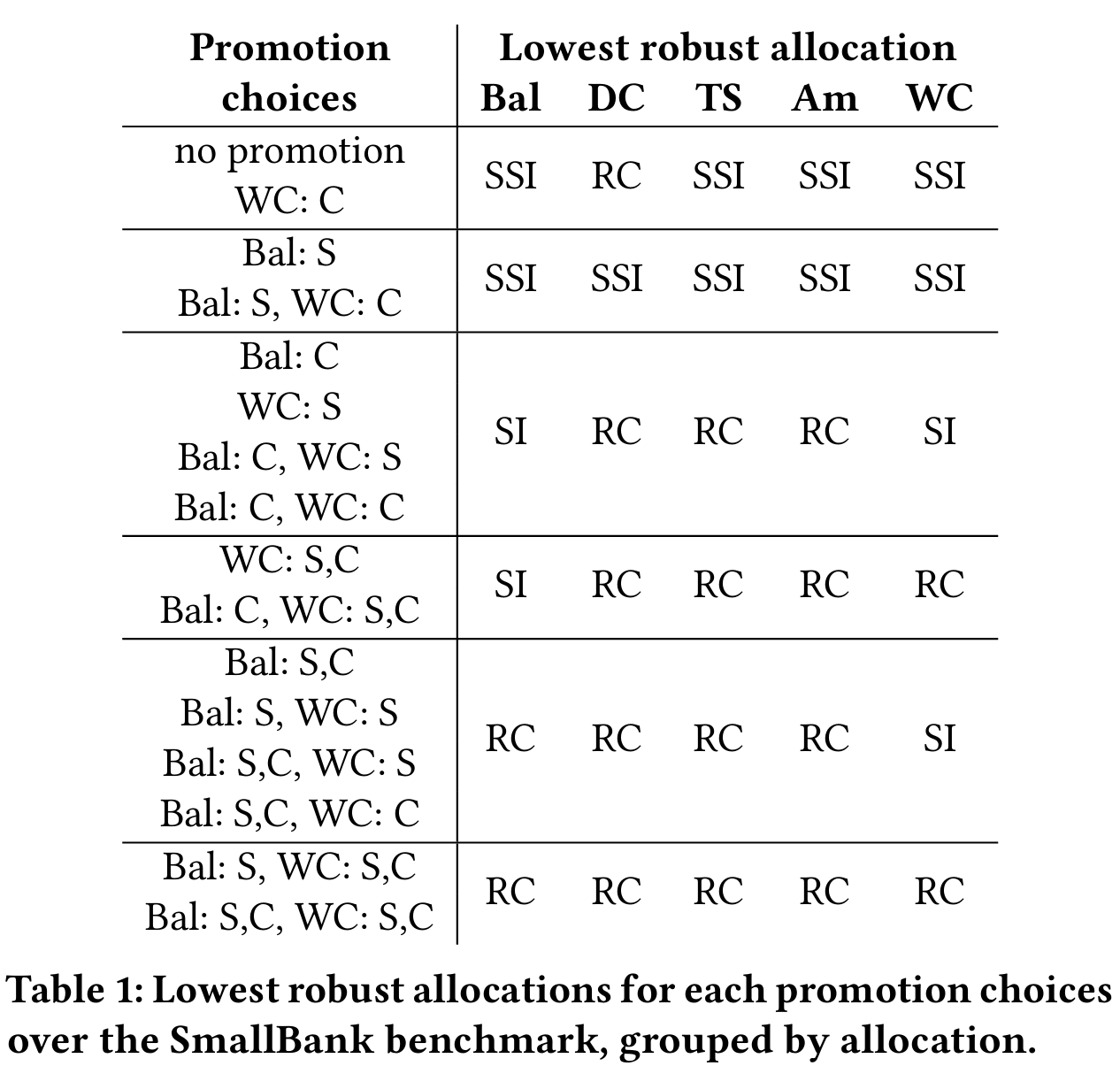
所考虑的任何隔离级别都不允许脏写。这迫使一个事务在覆盖之前事务所做的更改时，必须等到之前的事务提交或中止。因此，如果我们将一个读取操作提升为更新操作（即一个读取操作将观察到的值写回去），事务的语义不会受到影响，但最低健壮分配可能会有所不同。忽略 Account 表中只读的读取操作，SmallBank 基准中包含了 4 个可以提升的读取操作，这些操作位于 Savings 和 Checking 关系中，共计 16 种可能的提升选择。对于每种提升选择，我们运行算法来检测最低的健壮分配。生成的分配总结见表 1。我们通过提升的读取操作来表示每种提升选择。例如，Bal: S, WC: C 表示在 Balance 程序中提升 Savings 关系的读取操作，在 WriteCheck 程序中提升 Checking 关系的读取操作。为了方便起见，这些提升选择按其最低的健壮分配进行分组。请注意，没有提升的情况下，如前所述，只有五个程序中的一个（即 DepositChecking）可以在低于 SSI 的隔离级别下执行，而不放弃序列化性。此外，稍微提升一些读取操作就能很快得出健壮分配，在这种分配中几乎所有程序都在 RC 下执行。然而，最佳的提升选择不一定是允许最多程序在 RC 下运行的选择，原因很简单：新引入的写操作可能会对总体性能产生负面影响。因此，需要通过吞吐量实验来确定最佳的提升选择，我们将在下一节中进行讨论。

EVALUATING REPMILA OVER SMALLBANK

ALLOCATION ALGORITHM

Transactions and Schedules

Conflict-Serializability

Isolation Levels

定义 4.3

调度 $s$ 中的事务 $T_i$ 在 RC 下允许，当且仅当：

  • $T_i$ 中的每个写操作遵守 $s$ 的 commit order；
  • 每个读操作 $b_i \in T_i$ 都读到了 $b_i$ 在 $s$ 中的上一个相关写（read-last-committed）；
  • $T_i$ 在 $s$ 中不产生脏写。

调度 $s$ 中的事务 $T_i$ 在 SI 下允许，当且仅当：

  • $T_i$ 中的每个写操作遵守 $s$ 的 commit order；
  • 每个 $T_i$ 中的读操作都读到了 $first(T_i)$ 在 $s$ 中的上一个相关写（read-last-committed）；
  • $T_i$ 在 $s$ 中不产生并发写。

RC 与 Gotsman 体系的对比：

  1. RLC 与 Ext 不同，两者并无包含关系，可能导致不同的读结果；
  2. 调度分析承认（非分布式系统）单调时间戳，本身保证了 TranVis 和 Prefix；

因此，把 RC 的 RLC 换成 Ext 公理，则 RC 达到了 PC 的水平。

调度 $s$ 中的危险结构 $T_1 \to T_2 \to T_3$ 是：

  • $T_1 \xrightarrow{\rw} T_2 \land T_2 \xrightarrow{\rw} T_3$；
  • $T_1$ 和 $T_2$ 在 $s$ 中并发；
  • $T_2$ 和 $T_3$ 在 $s$ 中并发；
  • $\C_3 \le_s \C_1 \land \C_3 <_s \C_2$；
  • 如果 $T_1$ 是只读，则 $\C_3 <_S first(T_1)$。

本文中的 dangerous structure 定义比 [Fekete SIGMOD’08] 中的更强，Fekete 的定义仅要求两个连续的 $\rw$ 边。

定义 4.5

事务集合 $\T$ 在其上的分配 $\A$ 下被允许，当且仅当：

  • $\forall T_i \in \T. \A(T_i) = \RC \implies T_i \models \RC$；
  • $\forall T_i \in \T. \A(T_i) \in \set{\SI, \SSI} \implies T_i \models \SI$；
  • 不存在三个 $\SSI$ 事务（不一定是不同事务）构成的危险结构 $T_i \rightarrow T_j \rightarrow T_k$。

Transaction Templates

Transaction and Template Robustness

Deciding Template Robustness

Finding Lowest Robust Allocations

定义 4.10

命题 4.12

CONCLUSIONS