题目描述
牛牛有一块蛋糕,他想把蛋糕分给小朋友们。蛋糕一开始是圆形的,牛牛会在圆周上选择 $n$ 个不重合的点,将这几个点两两用线段连接。这些线段将会把蛋糕分成若干块。
现在,牛牛想知道,蛋糕最多会被分成多少块,请你告诉他答案。
输入格式
输入包含至多 $20$ 行,每行一个整数 $n$,含义见「题目描述」。保证 $0\le n \le 64$。
输出格式
依次回答牛牛的每个问题,对于每个问题,输出一行,包含一个整数表示答案。
输入输出样例 #1
输入 #1
1 | |
输出 #1
1 | |
说明/提示
样例解释
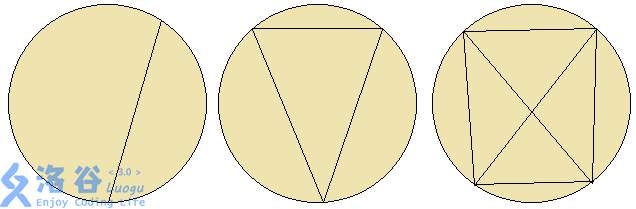
版权信息
来自 THUPC(THU Programming Contest,清华大学程序设计竞赛)2019。
题解等资源可在 https://github.com/wangyurzee7/THUPC2019 查看。
题解
拓扑学中的欧拉公式描述了凸多面体(convex polyhedron)的顶点(V)、边(E)和面(F)之间的基本关系: $$ F - E + V = 2 $$ 其中 $F$ 是面数,$E$ 是边数,$V$ 是边的交点数。可用数学归纳法证明这一公式。
本题中:
-
顶点数 $V(n) = n + \binom{n}{4}$。
- $n$:圆上原本的点的数量。
- $\binom{n}{4}$:任意四个点形成的两条线段均会产生一个交点。
-
边数 $E(n) = n + \binom{n}{2} + 2\binom{n}{4}$。
- $n$:圆上原本的 $n$ 个点将圆分成了 $n$ 条弧。
- $\binom{n}{2} + 2\binom{n}{4}$:每两个点之间存在一条线段。每一个交点会将相交的两条线段分成四部分,即增加两条线段。
因此,$F(n) = n + \binom{n}{2} + 2\binom{n}{4} - n - \binom{n}{4} + 2 = 2 + \binom{n}{2} + \binom{n}{4}$。
注意到平面图包含无限面,而应该计算的是圆内的区域,因此答案为 $F(n) - 1$。

