题目背景
这个三角图真好看。。
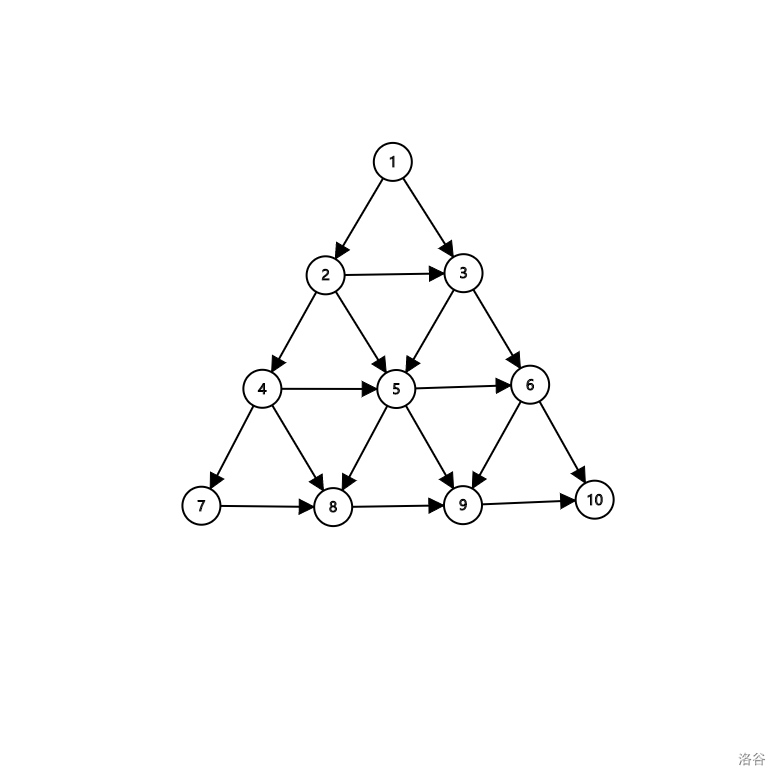
这个是 ${\rm 4}$ 阶三角图。。
题目描述
现在我们定义一个三角图是像上面一样的图。
请求出一个无限大的三角图从 $1$ 号点走到 $u$ 号点的方案数。
有 $T$ 组询问。
输入格式
第一行一个正整数 $T$。
第二行 $T$ 个正整数 $u_i$。
输出格式
$T$ 行,共 $T$ 个正整数,表示答案模 $998244353$ 的结果。
输入输出样例 #1
输入 #1
1 | |
输出 #1
1 | |
说明/提示
${\rm Subtask 1(10\ pts)}$:$1 \leq T \leq 100, \qquad 1 \leq u_i \leq 55$
${\rm Subtask 2(20\ pts)}$:$1 \leq T \leq 100, \qquad 1 \leq u_i \leq 12502500$
${\rm Subtask 3(30\ pts)}$:$1 \leq T \leq 100, \qquad 1 \leq u_i \leq 500000500000 \qquad u_i=\frac{x \times (x + 1)}{2}$
${\rm Subtask 4(40\ pts)}$:$1 \leq T \leq 100, \qquad 1 \leq u_i \leq 500000500000$
题解
给定三角网格图,求从点 $(1,1)$ 走到点 $(n,m)$ 的路径方案数。
首先将三角推平,变成这个样子:
1 | |
如果不走斜线,显然答案就是卡特兰数。总共向下走 $m-1$ 步,向右走 $n-1$ 步,方案数为:
$$ C_{n+m-2}^{m-1} - C_{n+m-2}^{m-2} $$
接下来考虑走斜线的情况。假设走了 $i$ 次斜线,那么向下走的次数变为了 $n' = n-1-i$,向右走的次数变为了 $m' = m-1-i$。
走直线的所有排列方案数为:
$$ C_{n'+m'}^{m'} - C_{n'+m'}^{m'-1} $$
根据插板法,插入走斜线的方案数为:
$$ C_{n'+m'+i}^{i} $$
根据乘法原理,总方案数为:
$$ \sum_{i=0}^{m-1} C_{n'+m'+i}^{i} \left[ C_{n'+m'}^{m'} - C_{n'+m'}^{m'-1} \right] $$

