$$ \def\vis{\mathsf{\textcolor{orange}{vis}}} \def\ar{\mathsf{\textcolor{pink}{ar}}} \def\RW{\mathsf{RW}} \def\WW{\mathsf{\textcolor{red}{WW}}} \def\WR{\mathsf{\textcolor{blue}{WR}}} \def\visa{\xrightarrow{\vis}} \def\ara{\xrightarrow{\ar}} \def\RWa{\xrightarrow{\RW}} \def\WWa{\xrightarrow{\WW}} \def\WRa{\xrightarrow{\WR}} \def\wri{\mathsf{wri}} \def\Stmts{\mathtt{Stmts}} \def\IF{\mathtt{IF}} \def\true{\mathsf{true}} \def\AccID{\mathtt{AccID}} \def\ID{\mathtt{ID}} \def\bal{\mathtt{bal}} \def\Amount{\mathtt{Amount}} \def\Alive{\mathtt{Alive}} \def\Fields{\mathtt{Fields}} \def\T{\mathcal{T}} \def\R{\mathcal{R}} \def\D{\mathcal{D}} \def\V{\mathcal{V}} \def\bbT{\mathbb{T}} \def\bbV{\mathbb{V}} \def\bbZ{\mathbb{Z}} \def\B{\mathbb{B}} \def\v{\mathtt{v}} \def\f{\mathtt{f}} \def\FOREACH{\texttt{ FOREACH}} \def\IN{\texttt{ IN}} \def\DO{\texttt{ DO}} \def\END{\texttt{ END}} \def\NULL{\texttt{ NULL}} \def\Vars{\texttt{ Vars}} \def\LVar{\texttt{ LVar}} $$
摘要
尽管近年来开发了许多弱一致性机制来提高分布式复制系统的性能并确保可用性,但确保在此类系统上运行的事务应用程序的正确性仍然是一个困难而重要的问题。可串行化是事务性程序的一个众所周知的正确性标准; 然而,了解应用程序在弱一致性环境中执行时是否可序列化仍然是一项具有挑战性的工作。在这项工作中,我们结合了基于依赖图的可串行化特征,并利用抽象执行框架来开发一种全自动方法,用于在任何弱一致性模型下静态查找有界可串行化违规。我们将可序列化问题简化为一阶逻辑(FOL)中公式的可满足性问题,这使我们能够利用现有 SMT 求解器的功能。我们提供了从用 SQL 编写的程序(允许循环和条件)自动构造 FOL 编码的规则,并将一致性规范表示为 FOL 公式。除了检测有界可串行性违规之外,我们还提供了两种正交方案,通过提供充分的条件(同样以 FOL 公式的形式)来推理无界执行,其可满足性意味着在任何任意执行中都不存在异常。我们已将所提出的技术应用于 TPC-C(一个具有复杂应用程序逻辑的现实数据库程序),并且能够发现并行快照隔离(PSI)下的异常,并验证快照隔离(SI)下无限执行的可串行性,两个远弱于可串行化的一致性机制。
Nagar 与 Jagannathan 在本文中使用一阶谓词逻辑公式对客户程序以及事务一致性模型进行精确建模,利用 SAT/SMT 自动推导出违反该一致性的执行历史的结构,并在客户程序可能产生的所有执行历史中搜索该结构。
本文的工作是基于分布式数据一致性。
TODO:SQL 中的循环是否是必须的?
作者:Kartik Nagar and Suresh Jagannathan, Purdue University, USA
Introduction
我们考虑检测在弱一致的复制分布式数据库中执行的事务程序的可序列化违规的问题。如果此类程序的执行等价于包含程序的事务的串行、顺序执行,则称其是可序列化的。确保此类程序的所有执行都是可序列化的,通过减少对理解顺序执行问题的复杂性,极大地简化了对程序正确性的推理。不幸的是,在不牺牲可用性(低延迟)[18] 的情况下,使用运行时同步机制强制执行可序列化性在地理复制分布式系统中是有问题的。为了获得可序列化性的正确性优势和高可用性的性能和可扩展性优势,我们研究了可以静态识别事务程序以始终产生可序列化执行的条件,而不需要全局同步。实现这一目标的挑战源于推理复制状态的复杂性,其中并非所有副本共享它们持有的数据的相同视图。
为了应对这一挑战,我们提出了一种全自动静态分析,它将程序中的显着依赖关系精确地编码为根据特定弱一致性模型的公理规范(§4)。然后,分析利用定理证明器系统地搜索这些执行中是否存在与这些依赖关系一致的循环;循环的存在表明可序列化违规(§5.1)。值得注意的是,我们的方法可以应用于任何弱一致性模型,其规范可以在一阶逻辑中表达,这是一个包含我们所知道的所有真实数据存储的类。更具体地说,我们的方法从输入程序构建一个依赖图[2],其中包含一个循环,然后询问在给定的一致性规范下是否存在有效的执行,这可能导致该图。为此,我们从可能发生依赖关系的事务程序条件中自动提取,并将依赖关系与基于事件的模型中的工件相关联,以找到是否存在与依赖图相对应的有效抽象执行。这些依赖关系以一阶逻辑公式编码,该公式只有在存在违反可序列化的执行时才可满足。
给定一个用 SQL 编写的事务程序,我们发现给定弱一致性模型下有界长度(bounded length)的可序列化违规(绑定限制了所考虑的并发事务实例的数量)。我们输出实际异常,包括所涉及的事务及其输入。然后可以使用此输出来加强异常中涉及的事务的一致性(甚至修改事务本身)。由于该方法在一致性策略上是参数化的,它还可以用于确定程序可序列化的最弱一致性策略。与其他用于检测例如并发程序[23]中的错误的有界验证技术一致,我们假设大多数可序列化违规将使用少量事务实例显现。
我们提供了两种正交方案,以使用无限数量的事务实例对任意长执行进行推理(§5.2、§5.3)。第一个方案形式化了足以检查有界执行中的可序列化违规的论点,通过证明超出该界限的较长违规会导致边界内的违规行为。第二个方案应用归纳参数来检查任意长执行中异常的缺失。我们的方法是 sound,但不是 complete——虽然所有发现的异常都由定理证明者提供的反例证明是 sound,但我们不能排除这两种方案无法识别的无界执行中出现的可序列化违规的可能性。
作为评估我们方法的适用性的严重案例研究,我们将我们的技术应用于 TPC-C、真实世界的事务程序和课程软件应用程序(§6)。在这两种情况下,我们能够在事件一致性和快照隔离(SI)的较弱变体(称为并行快照隔离 PSI [25])下检测多个可序列化违规,并验证当使用 SI 进行无界执行时,这些 amoies 不会发生。我们现在使用简单的示例概述我们的方法。
Overview
1 | |
chatPDF 存疑:
这段代码可以被编码为以下 FOL 公式:
$$ \left[(Exists(r, Account(r) \land AccID(r) = ID \land Balance(r) = bal))\right]_t,r \land bal > Amount \land V(\phi, \psi) $$
Account(r) 是一个谓词,表示 r 是一个账户记录。V(ϕ, ψ) 是一个评估函数,其中 ϕ 选择任意一个包含 $\withdraw$ 操作的循环的迭代,ψ 是 IF 语句的条件 bal > Amount 的值。如果 bal > Amount 为真,则更新 Balance 字段的值为 bal - Amount。
在上述公式中,更新操作并没有直接体现出来。这是因为在本文中,更新操作是通过对数据库状态进行修改来实现的,而不是通过修改 FOL 公式来实现的。在这种情况下,更新操作的效果可以通过修改数据库状态来实现,而不需要在 FOL 公式中显式地表示出来。因此,上述公式中只包含了 SELECT 语句和 IF 语句的条件,而没有包含 UPDATE 语句的具体实现。
在本节中,我们将展示如何发现可序列化违规,以及我们的分析的输出如何用于使用选择性同步修复违规。考虑一个简单的银行应用程序,它维护表帐户中多个帐户的余额,该帐户使用主密钥 AccID 进行索引,并包含字段平衡。考虑一个用 SQL 风格的语言编写的 $\withdraw$ 操作(如图 1 所示),它以 ID 和 amount 作为输入,如果余额足够,则从帐户数量 ID 中减去数量。假设应用程序部署在分布式复制环境中,这允许在可能不同的副本上并发调用 $\withdraw$ 操作,唯一保证提供最终一致性——最终,所有副本都将见证对 Balance 字段的所有更新。在最终一致性下,应用程序显然是不可序列化的,因为并发 $\withdraw$ 操作到同一个帐户——其总 $\withdraw$ 量超过帐户的平衡——都可以成功,这在可序列化的执行中是不可能的。
在这种情况下表达执行的一种方便方法是使用基于公理事件的表示。在这个框架中,抽象执行表示为元组 $(T, \vis, \ar)$,其中:
- $T$ 是事务调用的集合,
- $\vis \subseteq T \times T$ 是一个可见性关系,使得如果 $t \visa t'$,那么 t 的更新对 t' 可见;
- $\ar \subseteq T \times T$ 是一个仲裁关系,它完全对所有写入相同的位置进行排序,并确保最终的一致性[9]。
例如,如果 $t_1 = \withdraw(1,50), t_2 = \withdraw(1,60)$,则 $E = (\set{t_1, t_2}, \set{}, \set{(t_1, t_2)})$ 是一个抽象执行,不可序列化,因为帐户编号 1 中的余额的最终值将仅反映(reflect) $\withdraw$ 操作 $t_2$(假设 AccID 1 中的初始余额为 100),因为这两个操作之间没有强制执行可见性约束。这是丢失更新(lost update) [5] 异常的示例。我们的目标是自动构建这种异常执行。
检测序列化性违规的一种有用技术是从抽象执行中构建依赖图,然后在依赖图中搜索循环。依赖关系图的节点是调用,边表示它们之间的依赖关系。与可序列化性检测相关的依赖关系有三种类型:
- $t_1 \WRa t_2$ 是读依赖关系,这意味着 $t_2$ 读取由 $t_1$ 写入的值;
- $t_1 \WWa t_2$ 是写依赖关系,这意味着 $t_1$ 和 $t_2$ 都写入相同的位置,$t_2$ 的写入在 $t_1$ 之后仲裁;
- $t_1 \RWa t_2$ 是反依赖关系,这意味着 $t_1$ 不读取由 $t_2$ 写入的值,而是读取旧版本。例如,上面描述的异常执行 E 的依赖图如图 2 所示。
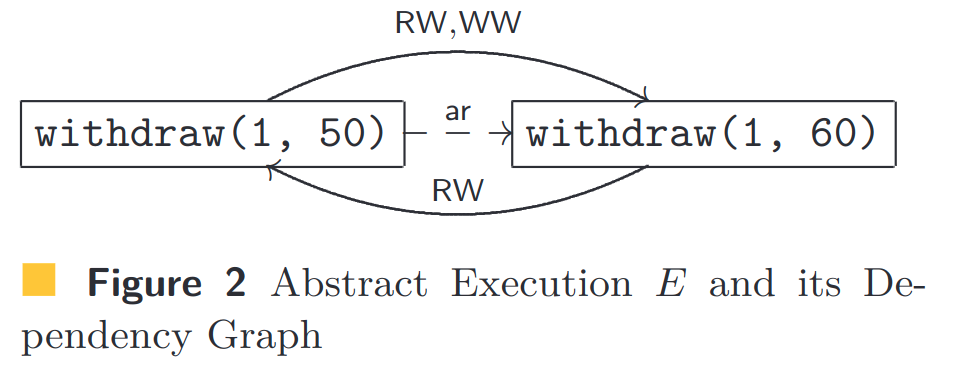
在我们的方法中,我们从包含循环的依赖关系图开始,然后询问与依赖关系图对应的执行是否可能。从事务代码中,我们自动提取在事务调用之间可以显示依赖边的条件。在我们正在运行的示例中,两个 $\withdraw$ 调用之间的依赖边(任何类型)只有在使用相同的帐户 ID 调用时才能显示。此外,我们将依赖边与相应抽象执行的关系 $\vis, \ar$联系起来。例如,$t_1 \RWa t_2 \Rightarrow \lnot(t_2 \visa t_1)$,因为否则,$t_1$ 将读取 $t_2$ 写入的值。这很有用,因为不同的一致性方案可以通过在 $\vis$ 和 $\ar$ 关系上设置约束来直观地表达。
为了防止在我们的运行示例中出现异常执行,我们可以使用并行快照隔离[25],它确保如果两个调用写入同一位置,则它们不能并发。虽然 PSI 是使用复杂的分布式协议来实现的,但在我们的抽象框架中,它可以简单地用以下约束来表示:
$\forall t, t'.t \WWa t' \Rightarrow t \visa t'$
现在,反常执行 $E$ 是不可能的,因为 $t_1 \WWa t_2 \Rightarrow t_1 \visa t_2$ 与 $t_2 \RWa t_1$ 相矛盾。
综上所述,以下是我们在 PSI 下为上述应用生成的公式的相关部分:
$$ \forall t, t' t \RWa t' \Rightarrow (\exists r.\AccID(r) = \ID(t) \land \AccID(r) = \ID(t') \land \bal(t') > \Amount(t')) \tag{1} $$
$$ \forall t, t', r.(\AccID(r) = \ID(t) \land \bal(t) > \Amount(t) \land \AccID(r) = \ID(t') \land \bal(t') > \Amount(t') \land t \ara t') \Rightarrow t \WWa t' \tag{2} $$
$$ \forall t, t'.t \RWa t' \Rightarrow \lnot(t' \visa t) \tag{3} $$
$$ \forall t, t'.t \WWa t' \Rightarrow t \visa t' \tag{4} $$
我们使用 $t, t'$ 表示事务的调用,$r$ 表示数据库中的记录。我们定义了 $\AccID$ 函数来访问记录的主键。类似地,$\ID, \Amount$ 等是将调用映射到其参数和局部变量的函数。两个调用之间的依赖关系的存在强制两个调用都必须访问的记录存在,以及执行访问所需的局部变量的条件(公式 1)。另一方面,如果两个调用保证写入相同的位置,它们之间必须存在 $\WW$ 依赖关系(公式 2。现在,不可能有调用 $t_1$ 和 $t_2$,遵守公式 2。(1)-(4)使得 $t_1 \WWa t_2$ 和 $t_2 \RWa t_1$ 是引起循环的必要条件,从而表现出串行性违反。
事实上,在 PSI 下,这个应用程序的依赖关系图中不可能有任意长度的循环。为了显示这一点,我们使用以下观察结果:由上述应用程序生成的依赖图中的任何长路径都将包含弦(chord),从而导致更短的路径。事实上,可以证明,在应用程序的任何依赖关系图中,任意两个调用之间的最短路径(如果存在路径)将始终小于或等于 3。这可以通过使用上述约束 (1)-(4)(并为 WR 边添加类似的约束),然后实例化长度为 4 的路径,使得路径中涉及的任何节点之间都没有弦,然后显示这种编码的不满意性来显示。因为一个循环也是一个路径,现在只检查长度为 3 的循环就足够了,因为任何更长的循环必然会产生一个长度小于或等于 3 的循环。
直观地说,这是在银行应用程序中发生的,因为两个节点之间存在任何依赖边意味着两个调用都必须访问同一个帐户,并且其中至少有一个必须执行写入。此外,任何两次写入总是通过 $\WW$ 边相关。现在,如图 3 所示,在依赖项中长度为 4 的任何路径图中,$t_1$ 或 $t_2$ 之一和 $t_4$ 或 $t_5$ 之一必须是一个 write,这意味着两个 write 之间的弦。因此,在 $t_1$ 和 $t_5$ 之间总是存在长度小于或等于 3 的较短路径。
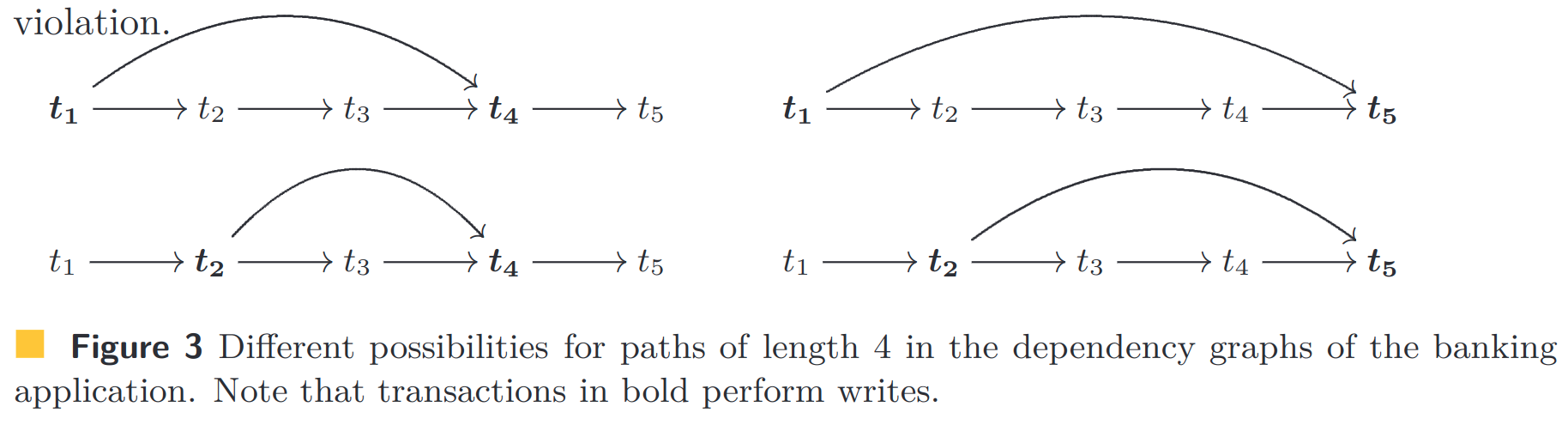
如果一个事务只有一个操作,那么这一结论总是成立的。这对工程上的优化有指导意义。
Preliminaries
Input Language and Database Mode

$\T$ 是事务程序,有一个在调用时被实例化的参数列表 $vlist$,和一组用于存储来自数据库的中间值的局部变量(通常作为 SELECT 查询的输出)。$\Stmts(\T)$ 表示 $\T$ 中的 SQL 语句(即 $\mathtt{INSERT, DELETE, DELECT, UPDATE}$)集合。
- $e_d$ 相当于 term;
- $\phi_d$ 是 SELECT 筛选记录的谓词,允许字段和值之间比较谓词的所有布尔组合;
- $\phi_c$ 是 SELECT 筛选变量用于 IF 判断的谓词,只允许使用局部变量和参数;
- 新增一列 $\Alive$ 表示当前记录是否在数据库表内。
为了简化演示,我们将假设只有一个表,并且每条记录都是由集合 $\Fields$ 索引的一组值。此外,所有 $\Fields$ 都存储整数值。$\mathtt{FOREACH}$ 循环在 $\v_2$ 中的一组记录上进行迭代,并在每次迭代期间将 $\v_1$ 分配给单个记录。我们将 $\v_2$ 称为循环变量。设 $\D(\v)$ 表示 $\v$ 的嵌套深度,如果 $\v$ 在任何循环之外被赋予一个值(或是一个参数变量),则嵌套深度为 0,否则为封闭循环的数量。对于在循环内分配值的变量 $\v$,对于所有 $1 \le i \le \D(\v)$,设 $\mathtt{LVar}(\v,i)$ 表示深度 i 处的循环变量。
SQL 语句使用谓词 $\phi _d$ 来选择将被访问/修改的记录,其中 $\phi _d$ 允许字段和值之间比较谓词的所有布尔组合。IF 语句 $\phi _c$ 中使用的条件只允许使用局部变量和参数。为了检查 SELECT 查询的输出是否为空,我们使用条件表达式 $\v = \NULL$,其中 $\v$ 存储查询的输出。
我们假设一个固定的非空字段子集是主键 PK。任何两条记录都必须在其至少一个 PK 字段中具有不同的值。假设有一个称为 $\Alive \in \Fields$ 的特殊字段,如果记录在数据库中,则值为 1,否则为 0。最初,所有记录都非 $\Alive$ 的。当将记录插入数据库中时,它变为 $\Alive$,当记录被删除时,它再次变为非 $\Alive$。
chatPDF,存疑:
这篇文章中提到了 SQL 语句的编码方式。SQL 语句使用谓词来选择将被访问/修改的记录,其中谓词允许在字段和值之间使用比较谓词的所有布尔组合。在 IF 语句中使用的条件语句($\phi_c$ )只允许使用局部变量和参数。为了检查 SELECT 查询的输出是否为空,我们使用条件表达式 v = NULL,其中 v 存储查询的输出。对于 WHERE 子句的编码,使用类似的过程。由于 WHERE 子句在记录上进行评估,因此编码专门针对记录和事务实例进行了优化。编码将字段访问替换为应用于记录 r 上的相应字段投影函数。请注意,字段投影函数仅用于在 WHERE 子句中访问的主键字段(表示为 $F \sube PK$)。所有类型条件和 WHERE 子句的完整编码可以在[24]的附录 A 中找到。
编码示例:
2
3
4SELECT * FROM my_table WHERE id = 1;
INSERT INTO my_table (id, name) VALUES (1, 'John');
UPDATE my_table SET name = 'Jane' WHERE id = 1;
DELETE FROM my_table WHERE id = 1;$$ \left[Exists(x, my_table(x) \land id(x) = 1)\right]_t,r\ \left[Exists(x, my_table(x) \land id(x) = 1 \land name(x) = 'John' \land Alive(x) = 1)\right]_t,r\ \left[Exists(x, my_table(x) \land id(x) = 1 \land name(x) = 'Jane' \land Alive(x) = 1)\right]_t,r\ \left[Exists(x, my_table(x) \land id(x) = 1 \land Alive(x) = 0)\right]_t,r $$
Abstract Executions
在我们的框架中,事务程序的执行使用基于[5]中使用的方法的事件结构来表示。事务实例的执行由事件组成,这些事件是数据库操作。数据库操作是对记录的字段的读取或写入。
$\mathcal{R} = \mathup{PK} \rightarrow \mathbb{Z}$ 是所有主键的集合。
所有数据库操作的集合表示为:
$$ \mathcal{O}=\set{\wri(r,f,n)|r \in \mathcal{R}, f\in \Fields \setminus PK, n \in \mathbb{Z}} \cup \set{\mathup{rd}(r,f,n)|r \in \mathcal{R}, f\in \Fields , n \in \mathbb{Z}} $$
为了简化表示,我们假设事务最多从记录的字段读取(写入)一次,并且不读取它写入、插入或删除的任何记录。这些假设允许我们忽略单个事务实例的事件之间的顺序。如果不满足这些假设,我们的方法可以很容易地进行调整。
这一假设过于简单,我们要处理的绝大多数数据库事务都是一个事务有多个事件。
Transaction

在这项工作中,我们将假设事务是在保证原子性和隔离性(也称为原子可见性[12])的环境中执行的。也就是说,要么事务的所有事件对其他事务可见,要么没有,并且同一组事务对事务中的所有事件可见。原子性和隔离性是事务程序的关键特性,两者都可以在复制的分布式环境中有效实现[9,3]。请注意,原子性和隔离并不能保证可序列化性,如§2 中的示例所示,我们的目标是在这种弱一致性的情况下探索可序列化性。
Abstract Execution

- $\sigma \visa \sigma'$ 表示前者的所有操作对后者可见;
- $\sigma \vdash o$ 表示前者执行了(包括了)后者。
Dependency Graph
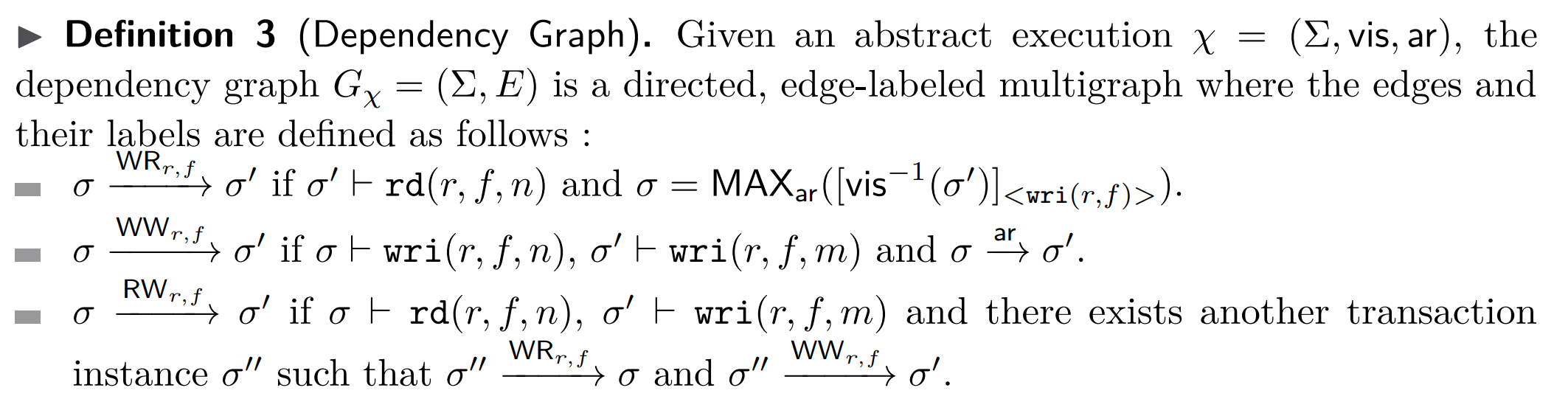
以上的三个语义是显然的。
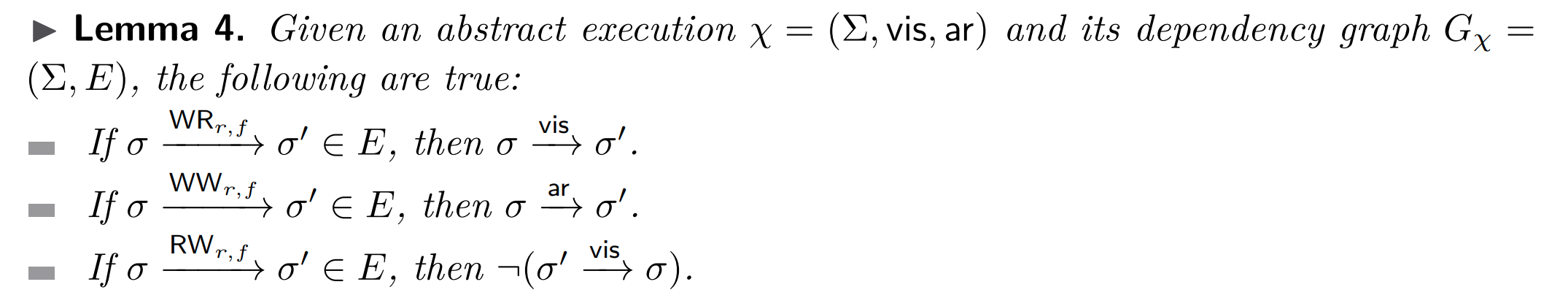
以上的三个语义是显然的。
Weak Isolation Models
不同的弱一致性和弱隔离模型可以通过对与抽象执行相关联的 vis 和 ar 关系施加约束来表达。这就产生了在特定模型下有效抽象执行的概念,即满足与这些模型相关联的约束的执行。下面,我们提供了几个已知的弱一致性和弱隔离模型的示例:

不同的模型也可以组合在一起以创建混合模型。例如,$\Psi_{\mathup{PSI}} \land \Psi_{\mathup{PC}}$ 等效于集中式数据库中的快照隔离 SI[4]。下面,我们在我们的设置中形式化了冲突可序列化性[6]的经典概念,然后将其与依赖图中循环的存在联系起来。

Operational Semantics
我们现在提出了一种操作语义,用于在一致性规范下从事务程序生成抽象执行。操作语义的目的是将 SQL 语句与抽象数据库操作联系起来,并证明我们在 FOL 中编码的合理性。在这里,我们只提供了一个非正式的概述,完整的操作语义可以在附录 B 中找到。
- $\mathcal{S}_{\mathbb{T, \Psi}} = (\Delta, \rightarrow)$ 是转换系统(transition system);
- $\Delta$ 是状态集,每个元素状态 $\delta \in \Delta$ 是以 $(\Sigma, \vis, \ar, \mathcal{P})$ 的形式存储的。
- $\Sigma$ 是已提交的事务实例;
- $\mathcal{P}$ 是事务实例的运行池。
转换有两种类型:
- 生成事务程序 $\T \in \bbT$ 的新实例,或者
- 在运行池中执行事务实例的语句。
当事务实例的新执行开始时,$\Sigma$ 的子集被非决定性地选择为对新实例可见。基于可见事务集和 ar 关系为新实例构建数据库视图(确保最后一个写入者获胜策略),并在此视图的基础上回答事务实例的所有查询。在任何时候,来自 $\mathcal{P}$ 的任何事务实例都可以被非决定性地选择用于执行其下一条语句。在事务实例执行期间生成的任何新事件都存储在运行池中。最后,当事务实例想要提交时,如果该实例要提交,则检查一致性规范($\Psi$)是否满足,如果满足,则将其添加到 $\Sigma$。我们现在可以根据转换系统的轨迹来定义有效的抽象执行:

Extended Version 附录 B 的操作语义(部分):这部分还没看懂。

FOL Encoding
Vocabulary
给定一组事务程序 $\bbT$ 和一致性规范 $\Psi$,我们现在展示如何在 FOL 中构造一个公式,使得 $\Psi$ 下 $\bbT$ 的任何有效抽象执行 $\chi$ 及其依赖图 $G_\chi$ 是符合公式的模型。编码以 $\bbT$ 和 $\Psi$ 作为参数。我们首先描述编码的词汇。我们定义了两个未解释的排序(sort) $\tau$ 和 $R$,使得 $\tau$ 的成员是事务实例,$R$ 的成员是记录。此外,我们还定义了一个包含事务类型的有限排序 $\bbT$,其中每种类型都是一个事务程序。
TODO:什么是排序?排序是指有序的集合吗?
函数 $\Gamma : \tau \to \bbT$ 将每个事务实例与其类型相关联。对于每个事务程序 $\T \in \bbT$ 和每个变量 $\v \in \Vars(\T)$,变量投影函数 $\rho_\v$ 给出事务实例中 $\v$ 的值。$\rho_\v$ 的签名取决于变量的类型以及它是否在循环中分配(赋值)。首先,让我们考虑在任何循环之外分配值的变量。在我们的框架中,变量有两种类型:值或一组值。此外,该值可以是整数(例如 $\withdraw$ 事务的参数 $\ID$)或记录。令 $\bbV = \bbZ \cup R$ 表示变量 $\v$ 的取值集合。如果 $\v$ 是一个值,$\rho_\v$ 具有签名 $\tau \to \bbV$,(即,$\rho_\v(t)$ 表示变量 $\v$ 在某个特定的事务实例 $t$ 中的值)。如果 $\v$ 是一组值,则 $\rho_\v$ 是一个谓词,其签名为 $\bbV \times \tau \to \B$,使得如果 $r$ 在事务实例 $t$ 中属于 $\v$,则 $\rho_\v(r, t)$ 为真。
考虑一个循环的形式:$\FOREACH \v_1 \IN \v_2 \DO c \END$。循环体(包括 $\v_1$)内赋值的所有局部变量都将由集合 $\v_2$ 中的值索引。因此,如果一个局部变量 $\v_3$ 在循环中被赋值,它是一个值,那么 $\rho_{\v_3}$ 将具有签名 $\bbV \times \tau \to \bbV$。另一方面,如果 $\v_3$ 存储一组值,则 $\rho_{\v_3}$ 将具有签名 $\bbV \times \bbV \times \tau \to \B$,并且解释如果 $\v_3$ 在 $\v_1$ 是 $r_1 \in \v_2$ 的迭代中包含 $r_2$,则 $\rho_{\v_3}(r_1, r_2, t)$ 为真。类似地,嵌套循环将具有由所有封闭循环中的记录索引的局部变量。
综上所述,$\rho_\v$ 的签名要么是 $\bbV^{\D(\v)} × τ \to \bbV$,要么是 $\bbV^{\D(\v) + 1} × τ \to \B$。与变量投影函数类似,为每个字段 $\f \in \Fields$ 定义字段投影函数 $\rho_\f : \R \to \bbZ$,使得 $\rho_\f(r)$ 给出记录 $r$ 中 $\f$ 的值。
我们定义谓词 $\WR, \WW, \RW$ 所有类型都是 $\tau \times \tau \to \B$,它们分别指定事务实例之间的读取、写入和反依赖关系。我们还定义了谓词 $\WR^R、\RW^R、\WW^R$ 所有类型都是 $\R \times \Fields \times \tau \times \tau \to \B$,它们通过指定导致依赖关系的记录和字段来提供更多上下文。谓词 $\vis, \ar$ 的类型都是 $\tau \times \tau \to \B$,指定事务实例之间的可见性和仲裁关系。谓词 $\Alive : \R \times \tau \to \B$ 表示记录在某事务实例中是否存活(存在)。
Relating Dependences with Abstract Executions
通过引理 4,在任何抽象执行中,两个事务实例之间的依赖边的存在强制对两个实例之间的 $\vis$ 和/或 $\ar$ 关系的约束。以下公式将此以及对 $\vis$ 和 $\ar$ 满足的基本约束进行编码:
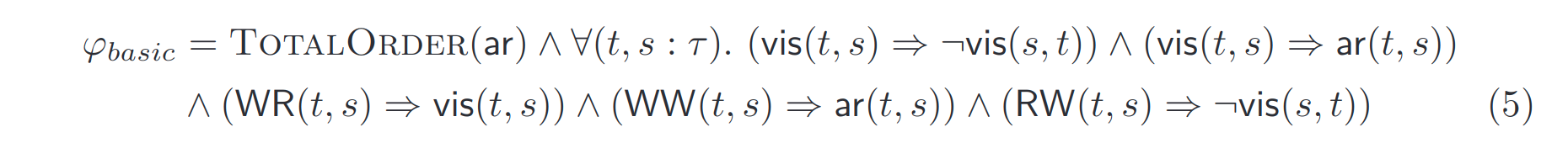
$\varphi_{basic}$ 中的规则都是显然的。
以下公式编码了一个基本的约束,涉及同一记录同一字段的依赖关系,因为最后一个写者赢得了数据库的性质:
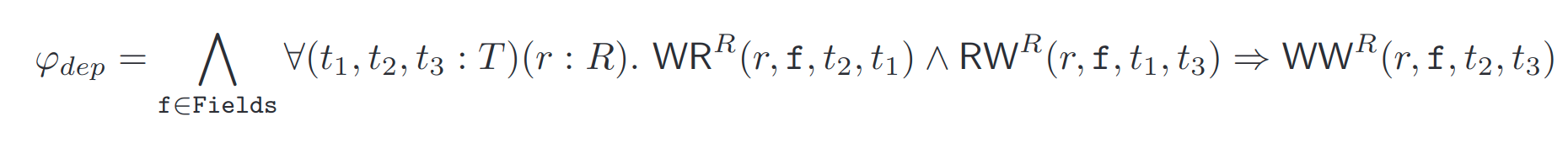
最后,一致性规范 $\Psi$ 可以使用词汇表中定义的关系和函数直接编码(我们用 $\varphi_\Psi$ 表示这个公式)。
Relating dependences with transactional programs
两个事务实例之间的依赖边的存在对生成实例及其参数的事务程序类型施加了约束。为了自动推断这些约束,我们使用以下策略:如果两个实例之间存在依赖边,那么事务必须存在两个访问公共记录的 SQL 语句。
为了对这一点进行编码,我们首先提取可以执行事务程序中 SQL 语句的条件。通过对事务 T 的代码执行简单的句法分析,我们从 $\Stmts(\T)$ 中的每个 SQL 语句中获得映射 $\Lambda_T$ 到封闭 $\IF$ 条件的结合(完整的算法可以在附录 A 中找到)。
通过将变量和字段分别替换为相应的变量投影和字段投影函数来构建程序中所有条件和 SQL 语句中的所有 WHERE 子句的 FOL 编码。这种编码的代表性规则集如图 4 所示。对于 IF 语句中使用的条件 $\varphi$,我们使用符号 $[\varphi]_t$ 来描述专门用于事务实例 t 的 FOL 编码。解释是,只有当条件 $\varphi$ 在事务实例 t 中为真时,$[\varphi]_t$ 才是可满足的。如果 $\varphi$ 在循环中,则如果 $\varphi$ 在 t 中的封闭循环的任何任意迭代中为真,则 $[\varphi]_t$ 一定是可满足的。出于这个原因,$[\varphi]_t$ 实际上表示为一个元组 $(\varphi, \psi)$,其中 $\varphi$ 选择任何任意的封闭循环迭代,公式 $\psi$ 是该迭代中条件的值。我们定义了一个评估函数 $\V(\varphi, \psi) = \varphi \land \psi$,它给出了最终的 FOL 编码。

公式 $\varphi$ 通过实例化属于所有封闭循环的循环变量的记录来选择迭代。例如,考虑 $\v = \NULL$ 的编码。在这里,$\varphi$ 实例化为属于 $\v$ 的每个包围循环的循环变量的记录(编码为 $\V([r_i \in \LVar(\v, i)]t)$),$ψ$ 编码所选迭代中 $\rho\v$ 对每个记录都是假的。类似地,在 $[r \in \v]t$ 的编码中,$\rho\v$ 在记录 $r$ 中必为真。在 $[\v_1 \in \v_2]_t$ 的编码中,我们首先获得 $\v_1$ 的值(元组 $[\v_1]_t$ 中的第二项),然后检查它是否存在于 $\v_2$ 中。
类似的过程用于获取 SQL 语句中使用的 WHERE 子句的编码。由于 WHERE 子句在记录上进行评估,因此编码专门用于记录和事务实例,为此我们使用符号 $[\varphi]{t,r}$。解释是,只有当记录 $r$ 上的事务实例 $t$ 为真时,$[\varphi]{t,r}$ 才是可满足的。编码将字段访问替换为应用于 $r$ 的相应字段投影函数。请注意,场投影函数仅用于 WHERE 子句中访问的主要关键字段(表示为 $F \subseteq PK$)。所有类型的条件和 WHERE 子句的完整编码可以在附录 A 中找到。
如前所述,我们的策略是根据访问公共记录来编码依赖边的必要条件。对于每对事务类型 $\T_1, \T_2 \in \bbT$,每个依赖类型 $\R \in \set{\WR, \RW, \WW}$,每对 SQL 语句 $\c_1 \in \Stmts(\T_1), \c_2 \in \Stmts(\T_2)$,由于语句 $\c_1$ 和 $\c_2$,我们计算依赖 $R$ 的必要条件 $\eta ^{\R\to,\T_1,\T_2 }_{\c_1,\c_2} (t_1, t_2)$ 对于依赖 $\R$ 存在于类型 $\T_1$ 和 $\T_2$ 的实例 $t_1$ 和 $t_2$ 之间。以下公式编码了两个事务实例之间的依赖关系可能是由于这些事务中任意两个 SQL 语句之间的依赖关系引起的这一事实:
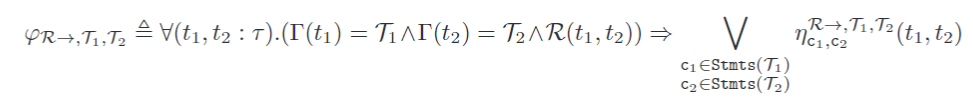
Applications
Bounded Anomaly Detection
Verifying Serializability : The Shortest Path Approach
Verifying Serializability : An Inductive Approach
Case Studies
我们开发了一个名为 Anode 的工具,它采用第 3.1 节中介绍的语言编写的一组程序和一致性规范,并使用第 4 节中介绍的编码规则自动生成 FOL 编码。我们使用 Z3 SMT 求解器来确定生成公式的满足性。为了评估我们方法的有效性,我们将所提出的技术应用于 TPC-C [1],这是一种著名的在线事务处理 (OLTP) 基准,广泛用于数据库社区,以及一个课程软件应用程序(用于 [19]),它是大学使用的课程注册系统的代表。
TPC-C:TPC-C 具有复杂数据库模式,具有 9 个表,在其 5 个事务中有复杂的应用程序逻辑。事务包含循环和条件,具有多个参数,并且根据参数值的行为不同;它们还使用复杂的查询,例如 SELECT MIN 和 SELECT MAX。据我们所知,这是第一个在弱一致性下验证 TPC-C 可序列化性的自动化静态分析。
在最终一致性下,TPC-C 有许多“丢失更新”异常,类似于第 2 节中描述的银行应用程序中的异常。这些异常的长度很小,并使用第 5.1 节中介绍的编码自动检测(k = 2)。为了摆脱这些异常,我们将一致性规范升级为 PSI[25]。在 PSI 下,我们没有发现 k = 2 或 k = 3 的任何异常,但对于 k = 4,发现了涉及 New-Order、支付和 Order-Status 事务的“长叉”异常,如图 5 所示。
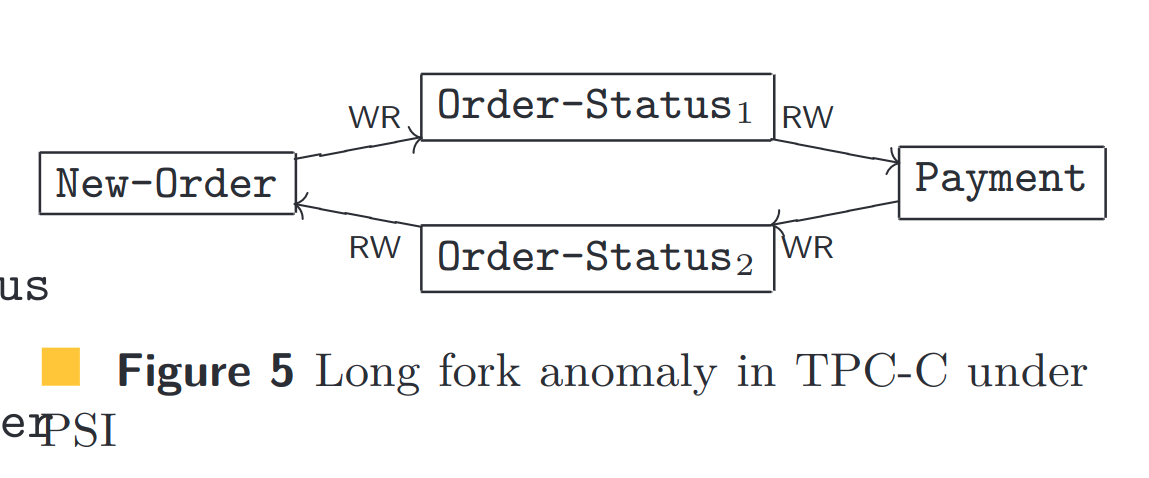
这种异常的发生是因为 New-Order 和 Payment 事务更新两个不同的表(Order 和 Customer 表 resp.),而 Order-Statustransaction 读取这两个表。由于 New-Order 和 Payment 事务之间没有同步,Order-Status1 有可能看到 New-Order 的更新,而不是 Payment 的更新,Order-Status2 则相反。我们还发现了一个类似的异常,涉及 New-Order 的两个实例和 Stock-level 事务的两个实例。
为了摆脱这些异常,我们进一步将一致性级别升级为快照隔离 (SI),之后我们没有发现 k = 4 的任何异常。然后,我们将注意力转向验证 SI 下 TPC-C 的可序列化性。我们首先尝试了最短路径方法(适用于银行应用程序),但我们能够在没有任何和弦的情况下发现长路径(可以任意扩展)。接下来,我们尝试了归纳方法,该方法成功地证明了 TPC-C 的可序列化性。具体来说,对于 T′ ={New-Order, Payment},公式 φInductive,T′ 显示为 UNSAT,其余 3 个事务 φInductive,{Delivery} 是 UNSAT。剩下的两个事务之间没有它们之间的任何依赖关系,这意味着 SI 下 TPC-C 的所有执行都是可序列化的。
Courserware:Courseware 应用程序维护课程和学生的数据库,并提供添加/删除学生和课程的功能,并将学生注册到课程容量的课程中。在 EC 下,我们的编码发现了以下异常:(1)两个并发的 Enroll 事务可能会注册超出课程容量的学生,(2)两个具有相同名称或两个具有相同名称的学生课程可以注册,(3) 学生可以注册一个同时删除的课程,或者学生同时被删除。请注意,所有这些异常都是为 k = 2 发现的。
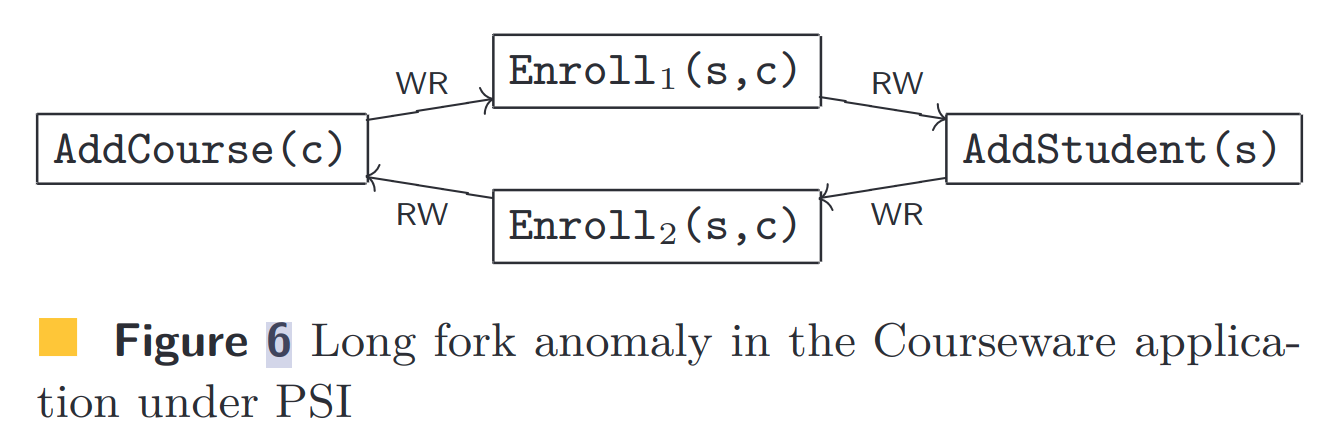
为了删除这些违规行为,我们以多种方式升级一致性模型:Enroll 事务升级为 PSI,而选择性可序列化性用于 AddCourse 和 AddStudent 的两个实例,以及 Enroll 和 RemCourse、Enroll 和 RemStudent 的实例。虽然这些升级处理了上述异常,但我们发现了一个新的长分叉异常(对于 k = 4),如图 6 所示。在这里,两个试图将学生(s)注册到课程(c)中的注册事务看到数据库的冲突视图,一个 Enroll 见证学生,而不是课程,反之亦然。我们注意到,虽然这是一个实际的可序列化违规,但它是完全无害的,因为见证不一致数据库状态的注册事务都将失败,因此最终的数据库状态与在执行结束时表现相同,其中两个注册都没有发生。这是我们分析的局限性,因为它没有提供任何方法来忽略无害的可序列化违规。我们计划在未来的工作中解决这个问题。
为了消除这种违规,我们将 Enroll 的一致性级别升级为 SI,之后我们没有发现任何异常。接下来,我们转向验证,在这里我们成功地能够使用最短路径方法,并证明长度大于或等于 8 的 Courserware 应用程序的任何依赖图中不存在最短路径。除了不存在长度小于或等于 8 的任何周期之外,这意味着应用程序的任何执行都是可序列化的。请注意,在所有情况下,求解器都在几个 (< 10) 秒中产生其输出。
Related Work and Conclusion
序列化是数据库社区中一个经过充分研究的问题,但缺乏静态自动化技术来检查数据库应用程序的可序列化性。Fekete 等人的早期工作。al.[17]和 Jorwekar 等人。al.[20]提出了轻量级句法分析,通过寻找应用程序静态依赖图中的危险结构来检查集中数据库中 SI 下的可序列化性(这是所有可能动态依赖图的过度近似)。最近的几项工作 [5, 12, 13, 14, 29, 27] 沿着这条线继续,方法是在不同的弱一致性机制下推导出依赖图中不同类型的危险结构,然后在静态依赖图上检查这些结构。
然而,静态依赖图是实际执行的高度不精确的表示,并且任何依赖于这些图的分析都可能产生大量的误报。事实上,一些作品 [5, 13, 14] 认识到这一点并提出了复杂的条件来减少特定一致性机制的误报,但这些工作没有提供任何自动化方法来检查实际程序上的这些条件。此外,应用程序逻辑可以防止这些有害的结构在实际执行中表现出来,例如在 TPC-C 中,它在 SI 下的静态依赖图中具有有害的结构,但没有出现在任何动态依赖图中。在我们的工作中,我们使用 FOL 精确建模应用程序逻辑和一致性规范,以便求解器会自动推导出在给定一致性规范下可能出现的有害结构,并在考虑应用程序逻辑的实际依赖图中搜索它们。
[8] 通过使用 FOL 编码构建具有循环的实际依赖图,提出了因果一致性下可序列化性的静态分析。虽然这项工作在精神上与我们的相似,但有几个关键点的差异:它们的可序列化性概念比我们的更强,因为它们允许事务在会话中组合在一起,串行顺序被迫适应会话顺序。虽然这简化了验证无界执行可序列化性的任务,但它也会导致大量无害的可序列化违规(为此他们提出了各种临时过滤方法)。此外,他们的重点是在高级数据类型而不是 SQL 程序上运行的程序,并且它们的分析不适用于一致性规范。
也有动态异常检测技术[28,11,7],这些技术要么在运行时构建依赖图并检查循环,要么分析执行后事件的跟踪。这些方法没有提供任何保证所有异常都将被检测到,即使对于有界执行也是如此。最近提出了许多方法[24,19,21,15],试图验证高级应用程序不变量在弱一致性下被保留。这些方法也是一致性规范的参数,但它们并不完全自动化,因为它们需要用户不变量形式的正确条件,并且它们不处理可序列化性。
总而言之,在本文中,我们迈出了第一步,为弱一致性下数据库应用程序的可串行化构建精确、全自动的静态分析。我们利用基于非循环依赖图的可序列化性和抽象执行框架来开发基于 FOL 的分析,该分析根据一致性规范进行参数化。我们展示了我们的方法如何用于检测有界异常,并在无界执行的特定条件下验证可序列化性。我们通过成功将其应用于真实世界的数据库基准来展示我们方法的实用性。
Appendix A: Complete FOL Encoding

过程 ExtractConds 获取事务程序 T 的代码,并填充从 $\Stmts(\T)$ 中的每个 SQL 语句到封闭 $\IF$ 条件中的公式的映射 $\Lambda_\T$。该过程是用所有初始谓词为 $\varphi = \true$ 的事务程序的代码调用的。

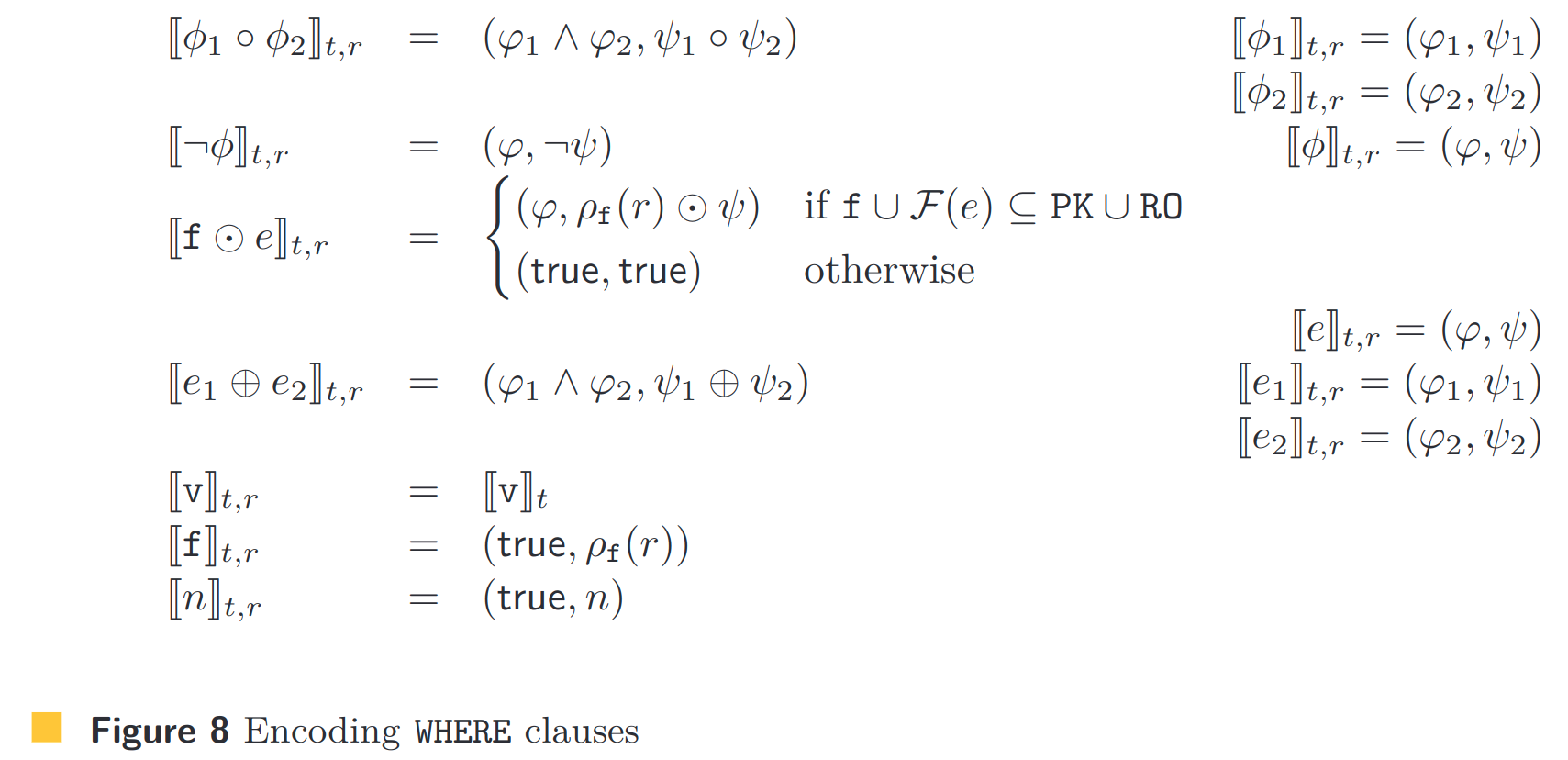
图 7 和图 8 显示了条件和 WHERE 子句的完整编码。请注意,field 投影函数仅用于 WHERE 子句中访问的主要关键字段。可以修改其他领域,因此这些领域中包含的值是记录和事务实例的函数,我们没有对其进行建模。这不会影响方法的 soundness,并且由于数据库事务中的大多数查询只使用主密钥字段,因此对精度的影响最小。作为优化,我们还发现在任何事务中从未修改过的只读字段(RO),并以与 PK 中的字段相同的方式处理 RO 中的字段。下面,我们将展示在我们的词汇表中可以编码几个已知的弱一致性规范:


我们现在介绍所有计算规则 $\eta ^{\R \to, \T_1,\T_2}_{c_1, c_2}$:

图 7 和图 8 显示了条件语句和 WHERE 子句的完整编码。请注意,字段投影函数仅用于在 WHERE 子句中访问的主键字段。其他字段可以修改,因此这些字段中包含的值是记录和事务实例的函数,我们不对其进行建模。这不会影响该方法的可靠性,而且由于数据库事务中的大多数查询只使用主键字段,因此对精度的影响很小。作为一种优化,我们还发现了在任何事务中从未修改过的只读字段(RO),并以与 PK 中的字段相同的方式处理 RO 中的字段。

下面,我们将展示如何在我们的词汇表中编码几个已知的弱一致性规范:

