软件工程理论基础-期末复习

$$ \def\TS{\mathrm{TS}} \def\Act{\mathrm{Act}} \def\AP{\mathrm{AP}} \def\Post{\mathrm{Post}} \def\O{\mathrm{O}} $$

摘要

题目 1-7 来自作业 1；

题目 8-12 来自作业 2；

13 及之后是考前划重点。

迁移系统

迁移系统表示为 $\TS = (S, \Act, →, I, \AP, L)$，其中：$S = \set{s_0, s_1, s_2, s_3, s_4}$ 为状态集合，$\Act = \set{\alpha, \beta, \gamma}$ 为动作集合，$I \subseteq S$ 为初始状态集合，$\AP = \set{a, b}$ 为原子命题集合，$L: S \to 2^{\AP}$ 为标签函数。

性质定义：

Action-Deterministic: $\forall s \in S \forall \alpha \in \Act. |I| \le 1 \land |\Post(s, \alpha)| \le 1$，其中 $\Post(s, \alpha) = \set{s' \in S \mid \exists (s, \alpha, s') \in →}$ 表示状态 $s$ 通过动作 $\alpha$ 能到达的后继状态集合；
AP-Deterministic: $\forall s \in S \forall A \in 2^{\AP}. |I| \le 1 \land |\Post(s) \cap \set{s' \in S | L(s') = A}| \le 1$。其中 $\Post(s) = \bigcup_{\alpha \in \Act} \Post(s, \alpha)$ 表示状态 $s$ 的所有后继状态集合。

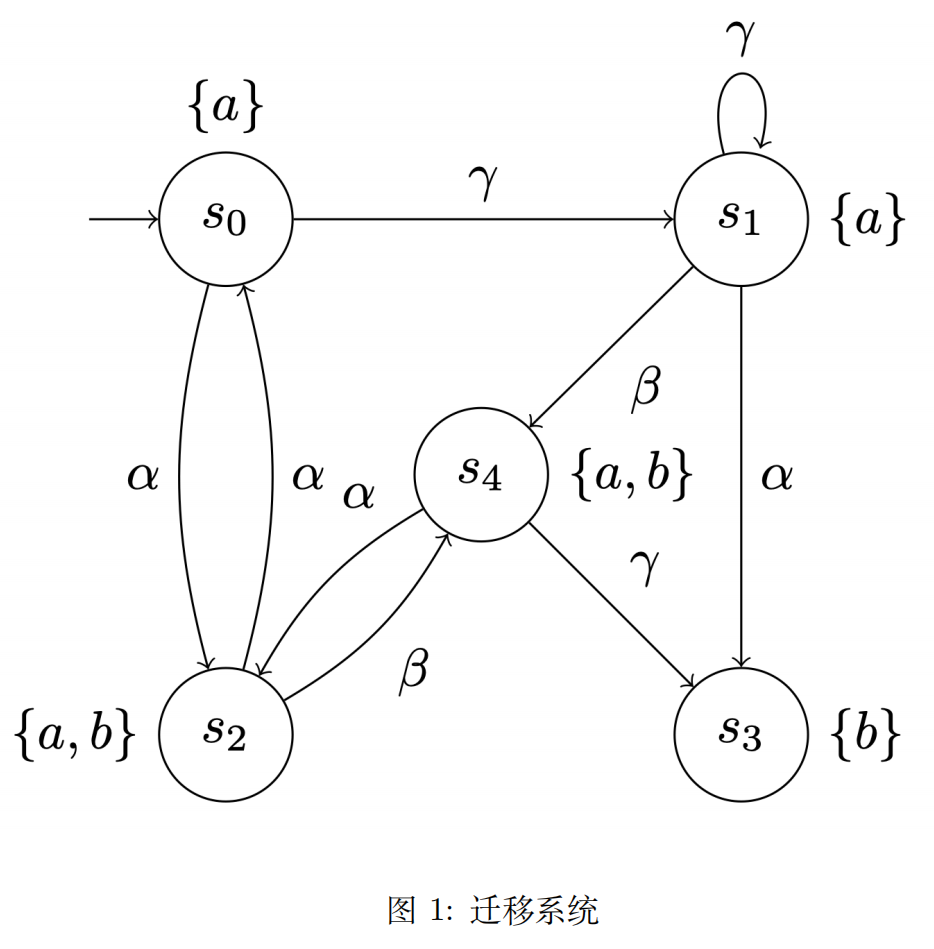
在图 1 所示的迁移系统中，显然对于每个状态节点，对于每个动作，从该节点出发的边都是唯一的，因此满足 Action-Deterministic 性质。

该迁移系统没有任何一个节点有标签相同的后继节点，该迁移系统满足 AP-Deterministic 性质。

进程执行

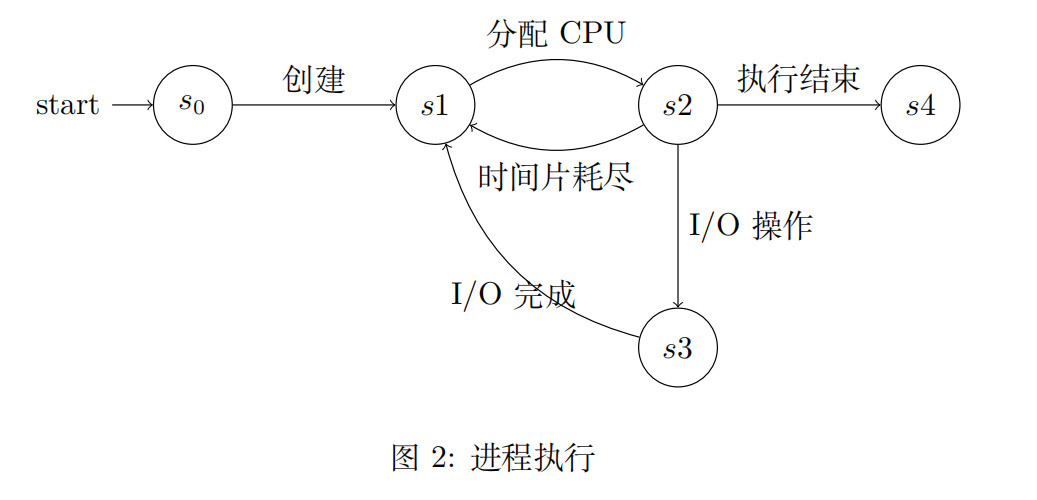
图 2 是一个进程执行的简单模型，其描述了进程执行的状态变化：

创建：进程被创建后，进入就绪状态，等待 CPU 分配。
分配 CPU：进程调度器选择某个就绪进程，将其分配到 CPU，进入运行状态。
时间片耗尽：进程由于时间片用尽，被抢占，回到就绪队列，等待下次调度。
I/O 操作：进程需要执行 I/O 操作（如读取磁盘、网络通信等），进入等待状态。
I/O 完成：进程的 I/O 操作完成，重新进入就绪队列。
执行结束：进程完成所有任务或遇到异常，进入终止状态，系统释放其占用的资源。

基于该模型，回答以下问题：

a. 给出两个无穷执行序列。

以下是两个无穷执行序列：

$$ s_0 \to s_1 \to s_2 \to s_1 \to s_2 \dots \tag{1} $$

$$ s_0 \to s_1 \to s_2 \to s_3 \to s_1 \to s_2 \to s_3 \dots \tag{2} $$

b. 针对问题 a 中的每个执行序列，写出两个其满足的 LTL 公式。

执行序列 $(1)$ 满足的 LTL 公式：

$$ \square \lozenge s_1 $$

$$ \square \lozenge s_2 $$

执行序列 $(2)$ 满足的 LTL 公式：

$$ \square \lozenge s_1 $$

$$ \square \lozenge s_2 $$

LTL 小结

LTL 符号	含义
$\square \varphi$	always
$\diamond \varphi$	eventually
$\text{O} \varphi$	nexttime
$\varphi \text{U} \psi$	until

CTL 小结

并发程序

假设程序 $P$ 有 $P_1, P_2, P_3$ 三个并行进程，进程 $P_i(1 ≤ i ≤ 3)$ 执行代码：

for k_i := 1 to 5 do {
	r_i := x // pc = 1
	r_i := r_i + 1 // pc = 2
	x := r_i // pc = 3
}

其中，x 为共享变量且初始值为 0，k_i 和 r_i 为 $P_i$ 的局部变量。针对程序 $P$，完成以下问题：

a. 使用 Transition System 建模该程序。

用迁移系统 $\TS = (\Sigma, T, I)$ 刻画程序 $P$ 的执行：

状态集合 $\Sigma$ 中的状态用元组 $\sigma = (x, k_1, pc_1, r_1, k_2, pc_2, r_2, k_3, pc_3, r_3)$ 表示，其中 $pc_i \in \set{1, 2, 3}$ 表示循环内下一步要执行的赋值语句编号。特别地，初始状态 $I = (0,1,1,0,1,1,0,1,1,0)$，$\Sigma_{end} = \set{\sigma = (x, k_1, pc_1, r_1, k_2, pc_2, r_2, k_3, pc_3, r_3) | k_1 = 6 \land k_2 = 6 \land k_3 = 6}$ 表示终止状态集合。

迁移规则 $T$ 中应当包括：

$$ t_0: pc_i = 1 \land k_i < 6 \to r_i = x \land pc_i = 2 \ t_1: pc_i = 2 \land k_i < 6 \to r_i := r_i + 1 \land pc_i = 3 \ t_2: pc_i = 3 \land k_i < 6 \to x = r_i \land pc_i = 1 \land k_i = k_i + 1 \ $$

对每个状态节点 $\sigma = (x, k_1, pc_1, k_2, pc_2, k_3, pc_3)$，根据 $k_i, pc_i$ 分情况讨论 $\sigma_i$。

以下是 $i = 1$ 的情况，对于 $i \in \set{2, 3}$，同理。

若 $k_1 = 6$，不存在 $s_1$，不需要添加新的迁移；

否则，添加新的迁移 $\sigma_0 \to \sigma_1$，其中：

若 $pc_1 = 1$，$\sigma_1 = (x, k_1, pc_1+1, x, k_2, pc_2, r_2, k_3, pc_3, r_3)$；

若 $pc_1 = 2$，$\sigma_1 = (x, k_1, pc_1+1, r_1+1, k_2, pc_2, r_2, k_3, pc_3, r_3)$；

若 $pc_1 = 3$，$\sigma_1 = (r_1, k_1+1, pc_1-2, r_1, k_2, pc_2, r_2, k_3, pc_3, r_3)$。

b. 当程序 P 执行结束，变量 x 的值是否可能为 2？若可能，给出一个对应的执行，否则给出简要说明。

x 的值可能为 2。下表是一个可能的执行。

原子操作编号 $P_1$ $P_2$ $P_3$

1 $k_2 = 1, r_2 = 0, x=0$

2 $k_2 = 1, r_2 := 1$

3 $k_1 = 1, 2, 3, 4$

4 $k_2 = 1, r_2 = 1, x:=1$

5 $k_1 = 5, r_1 := 1, x = 1$

6 $k_2 = 2, 3, 4, 5, 6$

7 $k_2 = 1, 2, 3, 4, 5, 6$

8 $k_1 = 5, r_1 := 2$

9

10 $k_1 = 5, r_1 = 2, x := 2$

算法建模

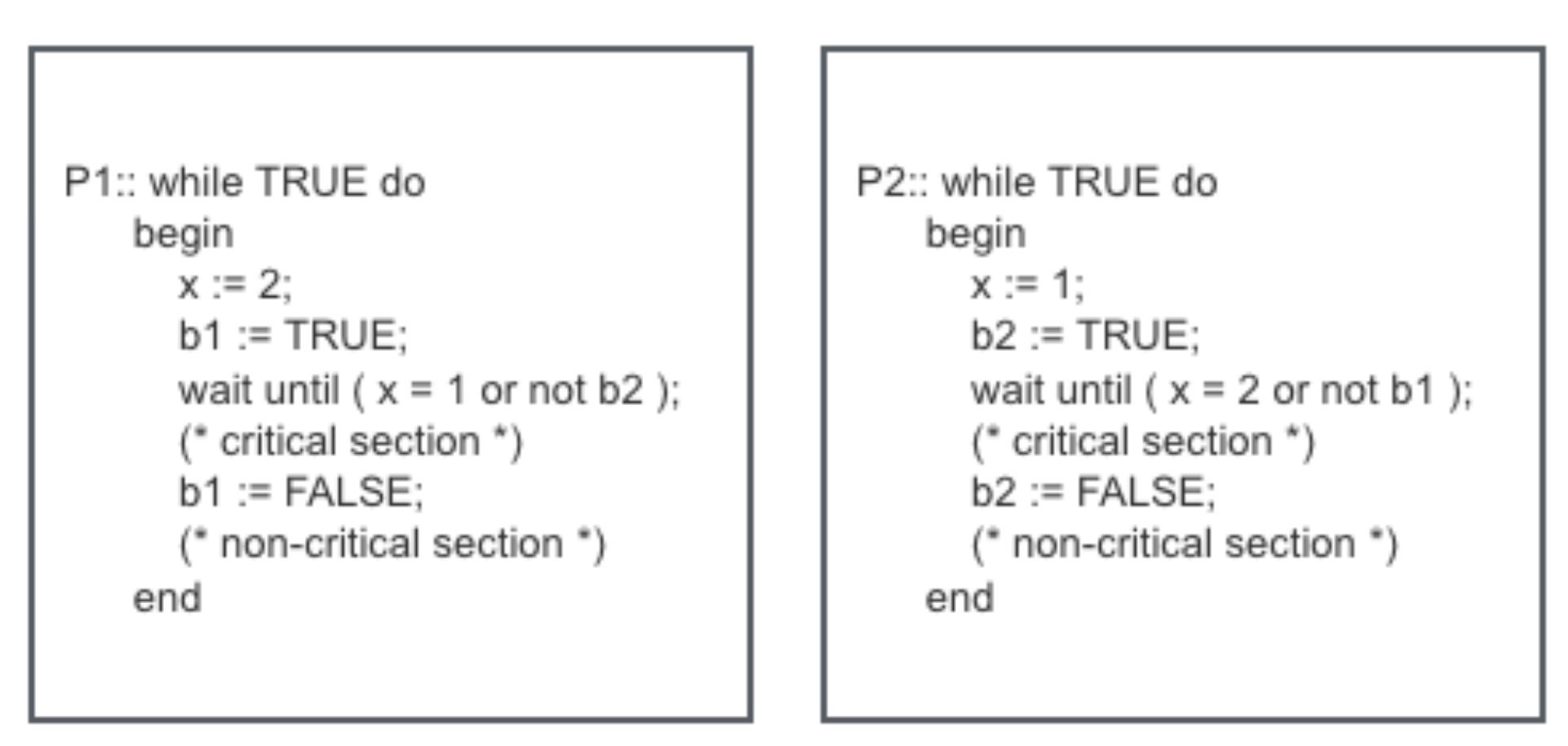
针对图 3 所示互斥算法，完成以下问题：

a. 使用 Transition System 建模该算法。

用迁移系统 $\TS = (\Sigma, T, I)$ 刻画算法执行：

状态集合 $\Sigma$ 中的状态用元组 $\sigma = (x, b_1, b_2, pc_1, pc_2)$ 表示，其中 $pc_1, pc_2$ 表示 $P_1, P_2$ 下一行要执行的原子代码编号。特别地，初始状态 $I = (1,\bot,\bot,1,1)$。

迁移规则 $T$ 中应当包括（其中 $i \in \set{1, 2}$）：

$$ t_1: pc_i = 1 \to pc_i = 2 \land x = 3 - i \ t_2: pc_i = 2 \to pc_i = 3 \land b_i = \top \ t_{3a}: pc_i = 3 \land (x = i \lor b_{3-i} = \bot) \to pc_i = 4 \ t_{3b}: pc_i = 3 \land \lnot (x = i \lor b_{3-i} = \bot) \to pc_i = 5 \ t_4: pc_i = 4 \to pc_i = 3 \ t_5: pc_i = 5 \to b_i = \bot \land pc_i = 6 \ t_6: pc_i = 6 \to pc_i = 1 \ $$

b. 在问题 a 的基础上，使用逻辑公式表达：两个进程不会同时进入临界区。

两个进程不会同时进入临界区表示为：

$$ \varphi \triangleq \lnot(pc_1 = 4 \land pc_2 = 4) $$

c. 判断问题 b 中的逻辑公式是否成立，若成立，请简要说明，否则给出反例（一个执行）。

b 中的逻辑公式不成立。

在下面这个反例执行中，两个进程同时进入临界区。

原子操作 $P_1$ $P_2$

1 $x = 2, b_1 = \bot, pc_1 = 1$

2 $x = 1, b_2 = \top, pc_1 = 2,3$

3 $pc_2 = 4$

4 $x = 1, b_1 = \top, pc_1 = 2, 3$ $pc_2 = 4$

5 $pc_1 = 4$ $pc_2 = 4$

原子操作	$P_1$	$P_2$
1	$x = 2, b_1 = \bot, pc_1 = 1$
2		$x = 1, b_2 = \top, pc_1 = 2,3$
3		$pc_2 = 4$
4	$x = 1, b_1 = \top, pc_1 = 2, 3$	$pc_2 = 4$
5	$pc_1 = 4$	$pc_2 = 4$

逻辑公式等价性判断

判断下列逻辑公式是否等价。若等价，给出证明，否则给出反例：

a. $F(pUq)$ 与 $(Fp)U(Fq)$

两者等价。

b. $Gp \land XFp$ 与 $Gp$

二者等价。

对于任何一个序列，若 $Gp \land XFp$ 为真，显然 $Gp$ 为真。

对于任何一个序列，若 $Gp$ 为真，该序列必然形式为 $ppp\dots$，该序列满足 $XFp$，因此 $Gp \land XFp$ 为真。

Büchi 自动机

Büchi 自动机概念

Büchi 自动机 (Büchi Automaton) 是一种理论计算机科学中的有限自动机，但它与我们常见的确定性有限自动机 (DFA) 或非确定性有限自动机 (NFA) 的核心区别在于其处理的输入。

传统自动机 (DFA/NFA): 处理有限长度的字符串。如果字符串处理完毕后，自动机停在一个接受状态，则该字符串被接受。
Büchi 自动机: 处理无限长度的字符串（也称为 ω-串或 ω-语言）。它的目的不是判断一个有限过程的结果，而是判断一个永不停止的无限过程的性质。

由于其处理无限序列的能力，Büchi 自动机在模型检测 (Model Checking) 和形式化验证 (Formal Verification) 领域至关重要，常被用来描述和验证系统的“活性属性”（Liveness Properties），例如“一个进程最终总会获得资源”或“一个请求最终总会被响应”。

一个 Büchi 自动机可以由一个五元组 $M = (Q, \Sigma, \delta, q_0, F)$ 定义，其中：

$Q$: 一个有限的状态集合。
$\Sigma$: 一个有限的字母表，即输入符号的集合。
$\delta$: 状态转移函数（或关系），形式为 $\delta: Q \times \Sigma \to 2^Q$。即根据当前状态和输入的符号，决定下一个可能的状态集合（因为它是非确定性的）。
$q_0$: 初始状态，是 $Q$ 中的一个状态。
$F$: 接受状态集，是 $Q$ 的一个子集 ($F \subseteq Q$)。

一个无限输入串 $w$ 被 Büchi 自动机接受，当且仅当它存在一个运行 $r$，这个运行无限次地访问了接受状态集 $F$ 中的至少一个状态。

作业题目

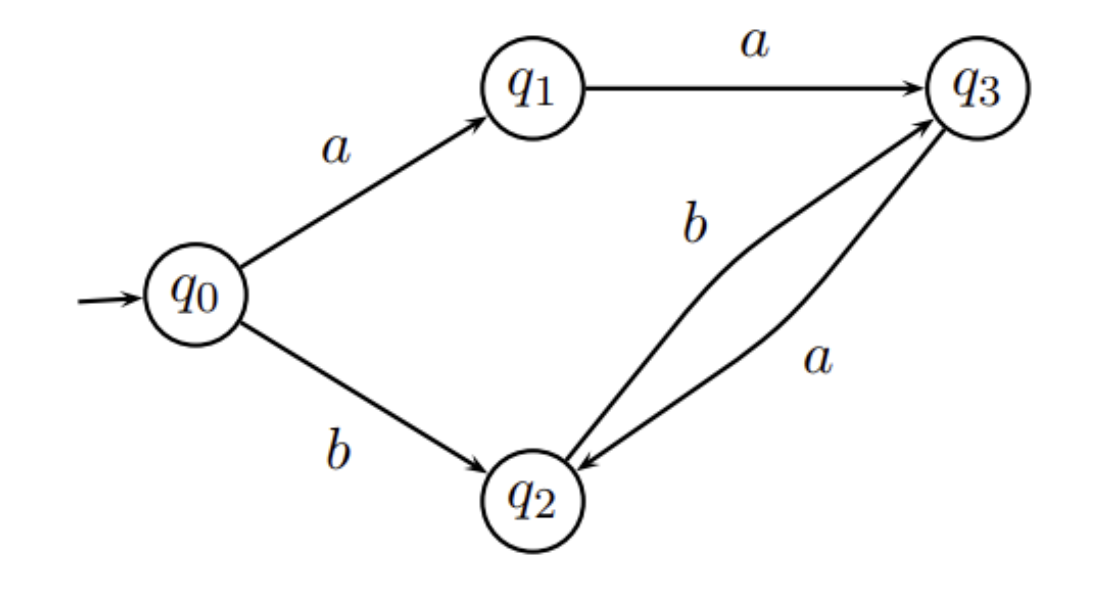
考虑以图 4 为基础的 Büchi 自动机，对于下列不同的接收状态集，判断该自动机的语言是否空：

a. $\set{q_0, q_1}$

语言为空，不可接受无穷字符串。

b. $\set{q_2, q_3}$

语言不为空，可接受无穷字符串 $bbababa \dots$。

c. $\set{q_1, q_3}$

语言不为空，可接受无穷字符串 $aaababa \dots$。

广义 Büchi 自动机转换

概念

对于广义 Büchi 自动机的接收集 $F$，有 $\forall S \in F. S \subseteq 2^{Q}$。一个无限输入串被接受，当且仅当它存在一个运行 $r$，这个运行无限次地访问了 $F$ 中的每一个集合中的至少一个状态。

例如，若 $F = \set{\set{q_1, q_2}, \set{q_3, q_4}}$，被接受的运行必然无限次的访问 $\set{q_1, q_2}$ 其中之一和 $\set{q_3, q_4}$ 其中之一。

特性	标准 Büchi 自动机 (BA)	广义 Büchi 自动机 (GBA)
接受状态集 F 的结构	一个单一的状态集合。$F \subseteq Q$。	一个由多个接受状态集组成的集合族。$F=\set{F_1,F_2,\dots,F_k}$，其中每个 $F_i \subseteq Q$。
接受条件	一个无限运行 (run) 被接受，当且仅当它无限次访问 $F$ 中的至少一个状态。	一个无限运行 (run) 被接受，当且仅当对于每一个接受集 $F_i \in F$，该运行都无限次地访问了 $F_i$ 中的至少一个状态。
直观理解	只需要满足一个“活性”目标（无限次进入 $F$）。	需要同时满足多个“活性”目标（无限次进入每一个 Fi）。

广义 Büchi 自动机转化为简单 Büchi 自动机

难以用语言描述，请自行询问大模型。

作业题

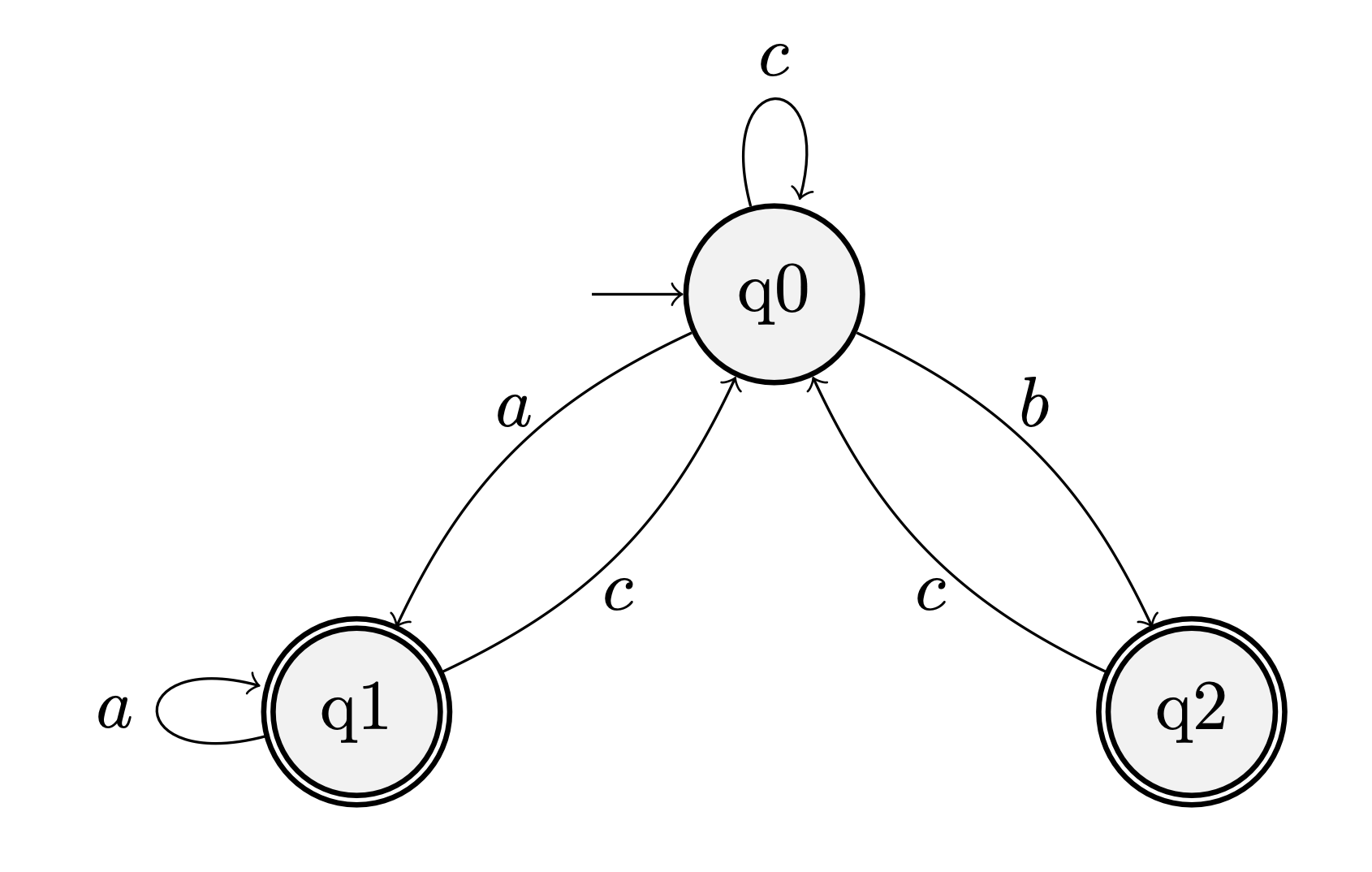
图 5 为以 $\set{\set{q_1}, \set{q_2}}$ 为接受状态集的广义 Büchi 自动机，请将其转换为简单 Büchi 自动机。

在上图中的广义 Büchi 自动机，一个运行被接受，当且仅当该运行无限次访问 $q_1$ 和 $q_2$。

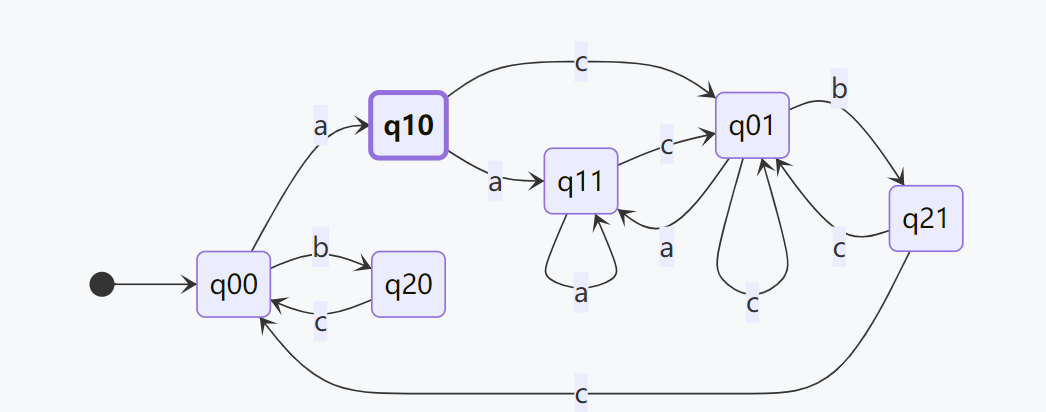
下图是转化后的简单 Büchi 自动机，其中粗边框节点为接受状态集。
> stateDiagram
direction LR

classDef endState font-weight:bold,stroke-width:3px,stroke:red  %% 定义结束状态样式

[*] --> q00
q00 --> q10 : a
q10 --> q11 : a
q10 --> q01 : c
q11 --> q11 : a
q11 --> q01 : c
q01 --> q11 : a
q01 --> q01 : c
q01 --> q21 : b
q21 --> q01 : c
q21 --> q00 : c
q00 --> q20 : b
q20 --> q00 : c

class q10 endState  %% 将q10标记为结束状态

公平性（Fairness）

公平性的理论基础

公平性主要用于排除那些在交错模型中可能出现，但与系统实际行为不符的执行序列。它约束了哪些序列可以被认为是有效的执行。

本题中的术语“转换（transition）”相当于 PL 或 DB 中所说的“原子操作”，而进程是比转换更大的粒度。

以下是这四种公平性的具体含义：

弱转换公平性（Weak transition fairness）：It cannot happen that a transition is enabled indefinitely, but is never executed.
弱进程公平性（Weak process fairness）：It cannot happen that a process is enabled indefinitely, but non of its transitions is ever executed
强转换公平性（Strong transition fairness）：If a transition is infinitely often enabled, it will get executed.
强进程公平性（Strong process fairness）：If at least one transition of a process is infinitely often enabled, a transition of this process will be executed.

四者的强弱关系为：

$$ 强转换 > \begin{Bmatrix} 强进程 \ 弱转换 \end{Bmatrix} > 弱进程 $$

在一个不公平的执行中，某个进程可能因为一直没有机会执行而被“饿死” 。公平性约束就是为了防止这种情况的发生，从而更准确地对系统行为进行建模和分析。

作业题

进程 A 和 B 分别使用如图 1 和图 2 所示方法申请被调度执行，图 3 所示调度器则用来调度进程 A 和 B。假设进程 A 和 B 可以同时执行，请问分别在哪些公平性（fairness）条件下，A 和 B 不会被“饿死”。

进程 A

while (true) {
    is_A_ready = true;
    for i := 1 to 10 {
        if is_A_scheduled {
            // do something
            break;
        }
    }
    is_A_ready = false;
}

进程 B

while (true) {
    is_B_ready = true;
    wait until is_B_scheduled {
        // do something
    }
    is_B_ready = false;
}

调度器

while (true) {
	if (is_A_ready == true) {
		is_A_scheduled = true;
	}
	if (is_B_ready == true) {
		is_B_scheduled = true;
	}
}

进程 A：就绪后多次申请执行，仅在强转换公平性下不会饿死；
进程 B：就绪后等待被调度执行，在四种公平性下都不会被饿死。

Binary Decision Diagram（BDD）

针对布尔函数 $$f(a,b,c) = (a \land b \land c) \lor (a \land (\lnot b) \land c) \lor ((\lnot a) \land b \land (\lnot c)) \lor ((\lnot a) \land (\lnot b) \land (\lnot c))$$ ，完成以下问题：

a. 以 $a < b < c$ 为顺序，写出对应的 BDD；

graph TD
    A[a]
    A0[b]
    A1[b]
    A -->|a=0| A0
    A -->|a=1| A1

    A00[c]
    A01[c]
    A10[c]
    A11[c]

    A0 -->|b=0| A00
    A0 -->|b=1| A01
    A1 -->|b=0| A10
    A1 -->|b=1| A11

    A000["1"]
    A001["0"]
    A010["1"]
    A011["0"]
    A100["0"]
    A101["1"]
    A110["0"]
    A111["1"]

    A00 -->|c=0| A000
    A00 -->|c=1| A001
    A01 -->|c=0| A010
    A01 -->|c=1| A011
    A10 -->|c=0| A100
    A10 -->|c=1| A101
    A11 -->|c=0| A110
    A11 -->|c=1| A111

b. 写出该 BDD 的 reduced form。

观察可知，函数可化简为 $f(a, b, c) = (a = c)$。

graph TD
    A[a]
    C0[c]
    C1[c]

    A -->|a=0| C0
    A -->|a=1| C1

    C0 -->|c=0| C00["1"]
    C0 -->|c=1| C01["0"]

    C1 -->|c=0| C01
    C1 -->|c=1| C00

对于布尔函数 $f(x,y) = x \lor y$ 和 $g(x,y) = x \land y$，回答下列问题：

a. 分别写出对应的 BDD；

graph TD
    X[x]
    Y[y]

    X -->|x=0| Y
    X -->|x=1| X1["1"]

    Y -->|y=0| Y0["0"]
    Y -->|y=1| X1

graph TD
    X[x]
    Y[y]

    X -->|x=0| X0["0"]
    X -->|x=1| Y

    Y -->|y=0| X0
    Y -->|y=1| Y1["1"]

b. 执行 $f \land g$ 运算，合并为一个 BDD。变量顺序均取 $x<y$。

合并后的 BDD 与 $g$ 相同，即：

graph TD
    X[x]
    Y[y]

    X -->|x=0| X0["0"]
    X -->|x=1| Y

    Y -->|y=0| X0
    Y -->|y=1| Y1["1"]

霍尔三元组（Hoare Tripe）

在下列霍尔三元组的空白处填写恰当的前置条件,使得对应的三元组成立。注意，前置条件应尽可能弱。

$$ \set{y = x^2}\ x := x + 1\ \set{y = x^2 - 2x + 1}\ y := y + 2 * x - 1\ \set{y = x^2} \ \set{x = w \land y = z}\ x := x + y;\ y := x - y;\ x := x - y\ \set{x = z \wedge y = w} \ \set{(a \ge b \to y = b * x) \land (a < b \to y = a * x)}\ \text{while } a < b \text{ do }\set{a := a + 1;\ y := x + y}\ \set{y = b * x} $$

完全正确性

请证明图 4 所示函数的完全正确性，即部分正确性和终止性。

我们在代码中添加循环不变式辅助证明：

/*@
  // Define the factorial function for ACSL specifications
  axiomatic Factorial {
	logic integer fact(integer n);

	// Recursive definition for fact(n)
	axiom fact_def_0: fact(0) == 1;
	axiom fact_def_n: \forall integer n; n > 0 ==> fact(n) == n  fact(n-1);

	// Property: factorial is non-negative for non-negative input
	axiom fact_non_negative: \forall integer n; n >= 0 ==> fact(n) >= 0;
  }
*/
/*@
  requires x >= 0;
*/
int f(int x) {
	int n = 0, y = 1;
	/*@
	  @ loop invariant n <= x;
	  @ loop invariant n >= 0;
	  @ loop invariant y == fact(n); // Re-added this crucial invariant
	  @ loop variant x - n;
	*/
	while (n != x) {
		n = n + 1;
		y = y * n;
	}
	// @ assert y == fact(x);
	return y;
}

部分正确性证明：在整个循环过程中，有循环不变量 y == fact(n)，且循环结束时循环变量 x - n == 0。因此返回值 y == fact(n) 是正确的。

终止性：循环变量 x - n 随着 n 的增大而减小，最终会减小到 0。因此函数必然会结束。

上述 ACSL 注解通过了 Frama-C 的验证。

证明完全正确性一般需要画流程图！

推理规则

Rust 是一种系统编程语言，旨在提供内存安全、并发支持和高性能，同时避免 C/C++ 中常见的安全问题（如空指针、数据竞争等）。Rust 通过所有权（Ownership）、借用（Borrowing）和生命周期（Lifetimes）等特性，在编译期防止空指针、悬垂引用和数据竞争，无需垃圾回收器。

在本题中，请针对图 5 所定义的程序，给出恰当的推理规则，进行“类型”和“借用”的检查。

示例：以 $\Gamma$ 表示程序上下文，谓词 $\text{Type}(x, T) / \text{Type}(e, T)$ 表示变量 $x$ / 表达式 $e$ 的类型为 $T$，谓词 $\text{Equal}(T_0, T_1)$ 表示类型 $T_0$ 和 $T_1$ 相同，则有

$$ \frac{\Gamma \models (\text{Type}(e, T_e) \land \text{Equal}(T_e, T))}{\Gamma \models \text{Type}(x, T)} \quad \text{let } x : T = e \ \frac{\Gamma \models (\text{Type}(e, T_e) \land \neg \text{Equal}(T_e, T))}{\Gamma \models \text{Error}} \quad \text{let } x : T = e $$

图 5：MiniRust

变量 $x \in \text{Identifier}$

整数值 $n \in \mathbb{Z}$

布尔值 $b ::= \text{true} \mid \text{false}$

类型 $T ::= \text{int} \mid \text{bool} \mid &T \mid &\text{mut } T$

表达式 $e ::= n \mid b \mid x \mid &x \mid &\text{mut } x \mid * x \mid e_1 + e_2 \mid e_1 == e_2$

语句 $s ::= \text{skip} \mid x = e \mid * x = e \mid \text{let } x : T = e; \mid s_1; s_2 \mid \text{if } (e) \set{ s_1 } \text{ else } \set{ s_2 }$

下面给出针对图 5（MiniRust）中表达式与语句的“类型检查”（Type Checking）和“借用检查”（Borrow Checking）推理规则。记程序上下文为 $\Gamma$，其中包含每个变量的静态类型和当前借用状态。谓词记为

$\Gamma \vdash e : T$ ：表达式 $e$ 的类型为 $T$；
$\Gamma \vdash s\ \mathbf{ok}$ ：语句 $s$ 在上下文 $\Gamma$ 下类型与借用均合法；
$\Gamma(x) = T$ ：变量 $x$ 在 $\Gamma$ 中的类型为 $T$；
$\mathit{Fresh}(\Gamma, x)$ ：在 $\Gamma$ 中 $x$ 尚未声明；
额外在 $\Gamma$ 中维护借用信息，如对每个变量记录可变借用次数与不可变借用次数（这里用注释说明，不在形式化中具体展开）。

表达式的类型检查规则

整数与布尔常量 $$ \frac{}{\Gamma \vdash n : \mathsf{int}} \quad \frac{}{\Gamma \vdash b : \mathsf{bool}} $$
变量 $$ \frac{\Gamma(x) = T}{\Gamma \vdash x : T} $$
不可变借用 $$ \frac{\Gamma(x)=T \quad \mathit{Can_Borrow_Imm}(\Gamma, x)} {\Gamma \vdash & x : &,T} $$
可变借用 $$ \frac{\Gamma(x)=T \quad \mathit{Can_Borrow_Mut}(\Gamma, x)} {\Gamma \vdash &!\mathsf{mut};x : &!\mathsf{mut},T} $$
解引用 $$ \frac{\Gamma \vdash x : &,T}{\Gamma \vdash *,x : T} \quad \frac{\Gamma \vdash x : &!\mathsf{mut},T}{\Gamma \vdash *,x : T} $$
算术与比较 $$ \frac{\Gamma \vdash e_1 : \mathsf{int} \quad \Gamma \vdash e_2 : \mathsf{int}} {\Gamma \vdash e_1 + e_2 : \mathsf{int}} \qquad \frac{\Gamma \vdash e_1 : T \quad \Gamma \vdash e_2 : T} {\Gamma \vdash e_1 == e_2 : \mathsf{bool}} $$

语句的类型与借用检查规则

跳过 $$ \frac{}{\Gamma \vdash \mathsf{skip};\mathbf{ok}} $$
普通变量赋值 $$ \frac{\Gamma \vdash e : T \quad \Gamma(x)=T \quad \mathit{No_Active_Mut_Borrows}(\Gamma, x)} {\Gamma \vdash x = e;\mathbf{ok}} $$
解引用左值赋值 $$ \frac{\Gamma(x)=&!\mathsf{mut},T \quad \Gamma \vdash e : T} {\Gamma \vdash *,x = e;\mathbf{ok}} $$
局部变量绑定（let） $$ \frac{\mathit{Fresh}(\Gamma,x) \quad \Gamma \vdash e : T_e \quad \mathit{Equal}(T_e, T)} {\Gamma \vdash \text{let } x : T = e;;\mathbf{ok}} \quad \frac{\Gamma \vdash e : T_e \quad \neg\mathit{Equal}(T_e, T)} {\Gamma \vdash \text{let } x : T = e;;\mathbf{Error}} $$
顺序组合 $$ \frac{\Gamma \vdash s_1;\mathbf{ok} \quad \Gamma' = \mathit{UpdateContext}(\Gamma, s_1) \quad \Gamma' \vdash s_2;\mathbf{ok}} {\Gamma \vdash s_1; s_2;\mathbf{ok}} $$
条件分支 $$ \frac{\Gamma \vdash e : \mathsf{bool} \quad \Gamma \vdash s_1;\mathbf{ok} \quad \Gamma \vdash s_2;\mathbf{ok}} {\Gamma \vdash \mathsf{if},(e),\set{s_1},\mathsf{else},\set{s_2};\mathbf{ok}} $$

考点

4.1 前面加一部分操作语义和等价性证明，参考 gotsman 2015

每一节前面有 general 的帽子

EDDG 的 general 的描述

找找实现 PC 的文献作为引用

Related Wrok：

一类工作：

第二类定义 IS

第三类对比鲁棒性

原子操作编号	$P_1$	$P_2$	$P_3$
1		$k_2 = 1, r_2 = 0, x=0$
2		$k_2 = 1, r_2 := 1$
3	$k_1 = 1, 2, 3, 4$
4		$k_2 = 1, r_2 = 1, x:=1$
5	$k_1 = 5, r_1 := 1, x = 1$
6		$k_2 = 2, 3, 4, 5, 6$
7			$k_2 = 1, 2, 3, 4, 5, 6$
8	$k_1 = 5, r_1 := 2$
9
10	$k_1 = 5, r_1 = 2, x := 2$