PLDI'21-Satisfiability Modulo Ordering Consistency Theory for Multi-threaded Program Verification

摘要

由于线程交错的数量很大，分析多线程程序是困难的。偏序关系可用于建模和分析多线程程序。然而，目前尚无专用的决策过程用于解决偏序约束。在本文中，我们提出了一种新颖的有序一致性理论，用于在顺序一致性下验证多线程程序，并详细阐述了其理论求解器。该求解器实现了增量一致性检查、最小冲突子句生成和专用理论传播，以提高 SMT 求解的效率。我们在可信赖的基准测试上进行了大量实验，结果显示我们的方法显著提升了性能。

作者：清华大学软件学院贺飞、Zhihang Sun、Hongyu Fan

Introduction

现在的计算系统中普遍使用共享内存多线程程序。并发程序的交错数量使得其在实践中很难进行验证。因此，开发技术来缓解并发程序验证中的执行爆炸问题是非常有意义的。

内存一致性模型[6]限制了来自不同线程的共享内存访问的执行顺序。它确定了读取访问可能返回的值。在本文中，我们遵循众所周知的顺序一致性（SC）模型[42]，其中执行路径是来自不同线程的指令的交错。

对于验证多线程程序，一种有希望的技术是使用有界模型检测[16, 19]，其中使用偏序关系来表示共享内存访问事件之间的 happens-before 关系[10, 11]。通过这种方式，可以指定多线程程序的不确定和复杂的交错行为。

一种常见的解决偏序约束的方法（例如[9–11, 50, 56]）是基于整数差分逻辑。每个事件与一个整数值时钟相关联，事件的顺序表示为这些时钟变量之间的差异。然后，可以使用整数差分逻辑的决策过程来解决偏序约束。这种方法为每个事件确定一个时钟值，这可能过于远大，因为我们只关心事件的顺序，而不关心它们的精确时钟值。

此外，在推理多线程程序时存在一个重要的公理（第 4 节中的公理 2），它定义了所谓的从读取顺序的推导规则。现有的方法[9–11, 29, 50]编码了所有可能的从读取约束，无论这些约束是否实际上需要进行验证。这种方法会产生大量的从读取约束，显著增加了求解器的负担并降低了其性能。

在本文中，我们提出了一种新颖的有序一致性理论（ $T_{o r d}$ ）（见第 4 节），并详细介绍了用于多线程程序验证的理论求解器（见第 5 节）。我们不再需要在编码公式中指定所有可能的从读取顺序。一个直接的好处是编码公式的大小显著减小。另一个好处是按需推导从读取顺序。通过使用专门的理论传播过程（见第 5.4 节），只有在相关变量被赋值时才推导出从读取顺序。这样，我们避免了生成大量无用的从读取约束。

我们为 $T_{o r d}$ 开发了一个高效的理论求解器，并将其集成到 DPLL(T) 框架中。给定一个部分赋值，求解器判断该赋值是否与理论公理一致，进而可以进一步简化为检测所谓事件图上的循环。特别地，我们使用了一种增量一致性检查算法（见第 5.2 节），该算法利用先前计算的结果并具有更高的效率。我们还设计了一个冲突子句生成算法（见第 5.3 节），用于找到不一致的最小原因。该算法的复杂度与冲突子句的数量和事件图中边的数量成线性关系。

最后但同样重要的是，受到单元子句传播思想的启发，我们提出了一种新颖的理论传播技术。我们尝试使用这种技术找到所谓的单元边，并使用这些边来强制一些未赋值的变量的取值（见第 5.4 节）。这样，DPLL(T)的决策迭代可以大大减少，并且整体性能得到显著提高。

我们在 CBMC [41]和 Z3 [23]中实现了所提出的方法，并在 SVCOMP 2019 的 ConcurrencySafety 类别中的 1061 个可信基准上进行了实验。我们将我们的方法与最先进的并发验证工具进行了比较，包括 CBMC [10]、Lazy-CSeq [36]、CPA-Seq [14, 15]和 Dartagnan [28]。相比于 CBMC、CPA-Seq 和 Dartagnan，我们的方法分别解决了更多的 38、119 和 897 个案例，比 Lazy-CSeq 少解决了 6 个案例。在解决了这些案例的基础上，与 CBMC、CPA-Seq、Dartagnan 和 Lazy-CSeq 相比，我们的方法运行速度分别提高了 2.33 倍、90.04 倍、139.47 倍和 7.20 倍，内存消耗分别减少了 18.7%、99.6%、99.0%和 94.5%。

我们还将我们的方法与最先进的无状态模型检测工具 Nidhugg/rfsc[4]和 GenMC [39]进行了比较，使用了 Nidhugg 套件中的 9 个基准。实验结果表明，随着程序规模（以轨迹数量衡量）的增加，我们的方法在大多数情况下优于这些工具。

总结起来，我们的主要贡献如下：

我们提出了一种新的适用于多线程程序验证的有序一致性理论 $T_{o r d}$ 。
我们详细介绍了一种高效的 $T_{o r d}$ 理论求解器，它实现了增量一致性检查、最小冲突子句生成和专门的理论传播，以提高 SMT 求解的效率。
我们在 CBMC 和 Z3 中实现了我们的方法。对 SV-COMP 并发基准进行的实验表明，我们的方法相比于最先进的工具有数量级的改进。

本文的其余部分组织如下。第 2 节介绍了一些背景知识。第 3 节展示了我们对多线程程序的符号编码。第 4 节提出了新的 $\mathcal{T}{ord} $理论。第 5 节开发了$ \mathcal{T}{ord}$ 的理论求解器。我们在第 6 节报告了实验结果，并在第 7 节讨论了相关工作。最后，第 8 节对本文进行了总结。

Preliminaries

Notions

在一阶逻辑中，术语是一个变量、一个常量，或一个 $n$ 元函数应用于 $n$ 个术语；原子式是 $⊥$ ， $⊤$ ，或一个 $n$ 元谓词应用于 $n$ 个术语；文字是一个原子式或它的否定。一个一阶公式是由文字使用布尔连接词和量词构建的。一个模型 $M$ 包含一个非空对象集 $dom (M)$ ，称为 $M$ 的域，一个将每个变量映射到 $dom (M)$ 中的对象的分配，以及分别为常量、函数和谓词提供的解释。一个公式 $Φ$ 是可满足的，如果存在一个模型 $M$ ，使得 $M ⊨ Φ$ ； $Φ$ 是有效的，如果对于任何模型 $M$ ， $M ⊨ Φ$ 。

一个一阶理论 $T$ 由一个签名和一组公理定义。签名包含允许在 $T$ 中使用的常量符号、函数符号和谓词符号；公理规定了这些符号的意义。 $T$ -模型是满足 $T$ 所有公理的模型。一个公式 $Φ$ 是 $T$ -可满足的，如果存在一个 $T$ -模型 $M$ ，使得 $M ⊨ Φ$ ； $Φ$ 是 $T$ -有效的，如果它被所有 $T$ -模型满足。

Satisfiability Modulo Theory and $DPLL (T)$

理论满足性模型问题（SMT）[12, 23, 24] 是一个决策问题，用于一些一阶背景理论组合的公式。对于每个背景理论 $T$ ，称为 $T$ -求解器的 $T$ -求解器，可以确定 $T$ 中任何文字的合取式的 $T$ -可满足性。

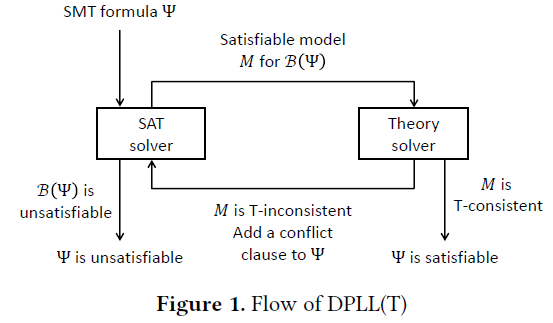
$DPLL (T)$ 是解决 SMT 实例的标准框架。它扩展了经典的 DPLL 算法[22, 45]，并带有专用的理论求解器。图 1 显示了 $DPLL (T)$ 的高级概述。给定一个 SMT 公式 $Ψ$ ， $DPLL (T)$ 首先用一个全新的布尔变量替换每个原子式。这个过程称为布尔抽象，因为结果公式 $B (Ψ)$ 相对于可满足性是原公式 $Ψ$ 的一个过度估计。 $B (Ψ)$ 的可满足性可以通过 SAT 求解器确定。如果 $B (Ψ)$ 是不可满足的，则 $Ψ$ 也是不可满足的；但反过来未必成立。如果 $B (Ψ)$ 是可满足的，并且 $M$ 是 SAT 求解器返回的满足模型，则我们需要继续检查 $M$ 是否与基本一阶理论一致。

理论求解器可以以在线或离线方案与 $DPLL (T)$ 集成。 $M$ 是当前（部分）对 $B (Ψ)$ 的赋值。在在线方案中， $T$ -求解器在 $M$ 改变时（即使 $M$ 是部分赋值）检查 $T$ -一致性；在离线方案中，一致性检查仅在 $M$ 是 $B (Ψ)$ 的满足模型时进行。如果 $M$ 是 $T$ -不一致的，则 $T$ -求解器尝试生成冲突子句并将其添加到子句集中，以防止求解器将来重复相同的路径。一个典型的理论求解器还支持理论传播，即通过理论公理推导未分配文字的值。

并发执行作为部分顺序

我们的方法基于 Alglave 等人的框架[10]，该框架使用部分顺序来建模并发执行。一个事件 $e$ 是一个读或写内存访问，具有以下属性：

$type (e)$ ： $e$ 的类型，即如果 $e$ 是写访问，则为 $W$ ；如果 $e$ 是读访问，则为 $R$ 。
$addr (e)$ ： $e$ 访问的内存地址。
$guard (e)$ ：使 $e$ 可用的守卫条件。

设 $E$ 为所有事件的集合。存在一些事件之间的关系。程序顺序关系 $≺_{po}$ 是来自同一处理器的事件的全序。写序列化关系 $≺_{ws}$ 是具有相同地址的写的全序。读-写关系 $≺_{rf}$ 将一个写事件 $e_{1}$ （ $type (e_{1}) = W$ ）与一个读事件 $e_{2}$ （ $type (e_{2}) = R$ ）联系起来，表示 $e_{2}$ 读取由 $e_{1}$ 写入的值。

此外，给定一对写事件 $e_{1}$ 和 $e_{2}$ （ $type (e_{1}) = type (e_{2}) = W$ ），以及一个读事件 $e_{3}$ （ $type (e_{3}) = R$ ），使得 $e_{1} ≺_{ws} e_{2}$ 和 $e_{1} ≺_{rf} e_{3}$ ，我们知道 $e_{1}$ 发生在 $e_{2}$ 之前，并且 $e_{3}$ 从 $e_{1}$ 读取。为确保 $e_{3}$ 不从 $e_{2}$ 读取， $e_{3}$ 必须发生在 $e_{2}$ 之前。我们将这样的关系称为来自读操作的关系 $≺_{fr}$ 。