多项式乘法
问题背景
给定两个多项式 $A(x)$ 和 $B(x)$:
$$ A(x) = a_0 + a_1x + a_2x^2 + \dots + a_nx^n \ B(x) = b_0 + b_1x + b_2x^2 + \dots + b_mx^m $$
我们需要计算它们的乘积 $C(x) = A(x) \cdot B(x)$。
根据定义,乘积 $C(x)$ 的系数 $c_k$ 为:$c_k = \sum_{i=0}^{k} a_i b_{k-i}$。这个形式的计算被称为卷积。如果我们直接按照这个定义进行计算,对于 $C(x)$ 的每一项系数,都需要 $O(k)$ 的时间。由于 $C(x)$ 的最高次项为 $n+m$,总的时间复杂度为 $O((n+m)^2)$,通常简记为 $O(n^2)$。当 $n$ 和 $m$ 的规模达到 $10^5$ 甚至更大时,这种朴素算法显然无法接受。
加速计算的思路:点值表示法
我们知道,一个 $n$ 次多项式可以被 $n+1$ 个不同的点唯一确定。例如,一条直线(1 次多项式)可以被两个点唯一确定,一条抛物线可以被三个点唯一确定。
这启发我们,除了用系数表示多项式,还可以用点值来表示。
- 系数表示法:$A(x) = \sum_{i=0}^{n} a_i x^i$
- 点值表示法:给定 $n+1$ 个不同的数 $x_0, x_1, \dots, x_n$,计算出 $y_i = A(x_i)$,则多项式 $A(x)$ 可以用点对集合 $\set{(x_0, y_0), (x_1, y_1), \dots, (x_n, y_n)}$ 来表示。
点值表示法的优势在于乘法运算。如果 $C(x) = A(x) \cdot B(x)$,那么对于任意一个 $x_i$,显然有 $C(x_i) = A(x_i) \cdot B(x_i)$。因此,如果 $A(x)$ 和 $B(x)$ 都在一组相同的点 $\set{x_0, x_1, \dots, x_{n+m}}$ 上求值,我们就可以在 $O(n+m)$ 的时间内计算出 $C(x)$ 在这些点上的点值。
这给了我们一个全新的计算流程:
- 求值(Evaluation):选择 $n+m+1$ 个点,分别计算出 $A(x)$ 和 $B(x)$ 在这些点上的点值。
- 点积(Pointwise Product):将 $A(x)$ 和 $B(x)$ 的点值对应相乘,得到 $C(x)$ 的点值。
- 插值(Interpolation):根据 $C(x)$ 的点值,反解出它的系数。
这个思路的关键在于如何快速地完成第一步(求值)和第三步(插值)。如果随机选取点,求值过程的复杂度依然是 $O(n^2)$。因此,我们需要找到一组特殊的点,使得求值和插值可以被加速。
快速傅里叶变换(FFT)
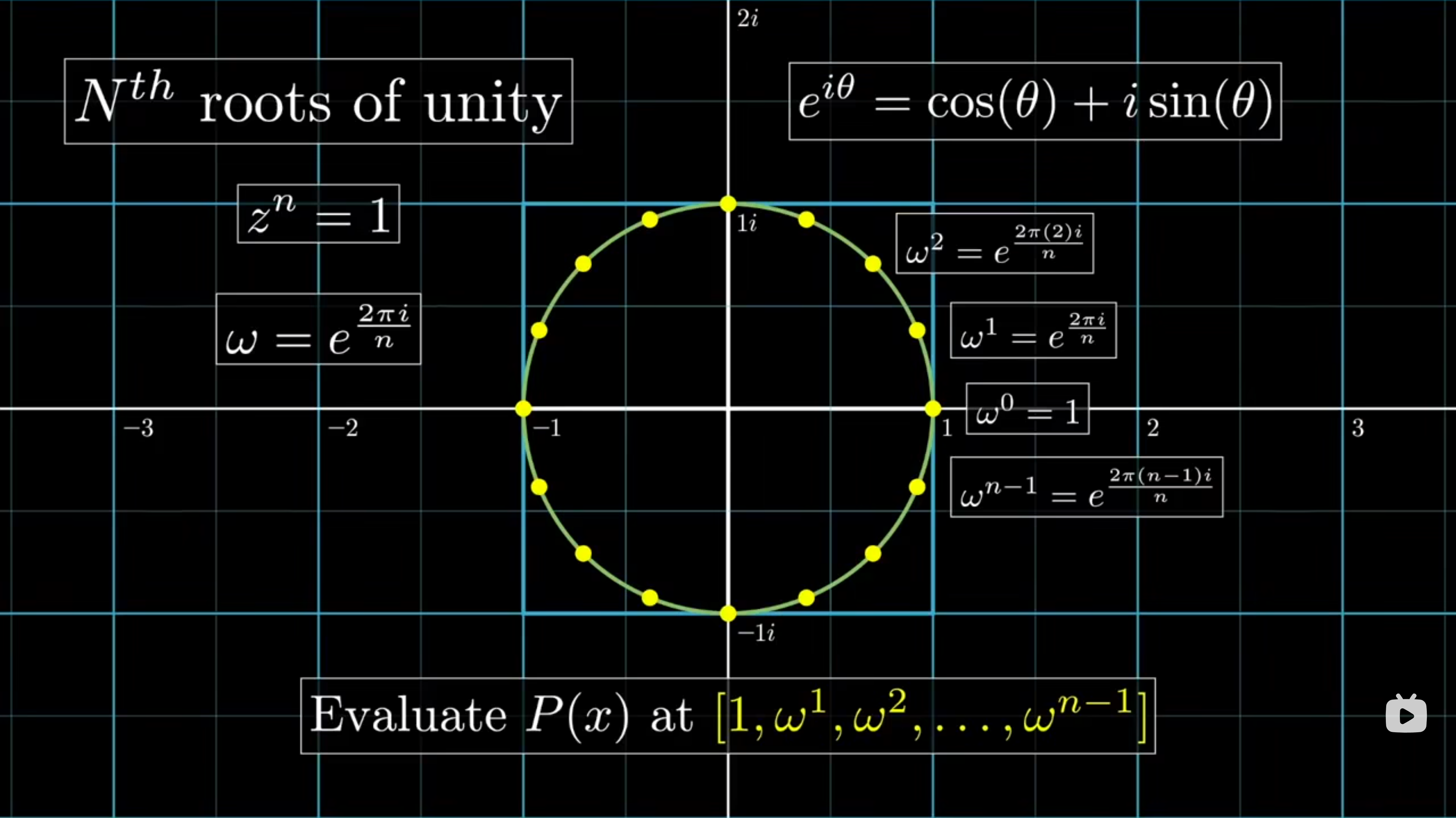
快速傅里叶变换(Fast Fourier Transform, FFT)就是实现上述快速求值和插值的关键算法。它巧妙地选取了一组特殊的复数——单位根,作为求值的点。
复数与单位根
- 复数:形如 $a+bi$ 的数,其中 $a$ 是实部, $b$ 是虚部,$i$ 是虚数单位,满足 $i^2 = -1$。复数可以在复平面上表示,对应坐标为 $(a, b)$。
- 欧拉公式:$e^{i\theta} = \cos(\theta) + i\sin(\theta)$。这建立了指数函数和三角函数之间的桥梁,几何意义是复平面上一个模长为 1,与正实轴夹角为 $\theta$ 的向量。
- $n$ 次单位根:满足方程 $z^n = 1$ 的复数解 $z$。根据欧拉公式,这些解恰好有 $n$ 个,它们是: $$ \omega_n^k = e^{i \frac{2\pi k}{n}} = \cos\left(\frac{2\pi k}{n}\right) + i\sin\left(\frac{2\pi k}{n}\right) \quad (k = 0, 1, \dots, n-1) $$ 其中 $\omega_n^k$ 表示第 $k$ 个 $n$ 次单位根。
单位根在复平面上均匀地分布在一个单位圆上,它们把圆 $n$ 等分,因此有性质:
- 周期性:$\omega_n^{k+n} = \omega_n^k$
- 对称性:$\omega_n^{k + \frac{n}{2}} = -\omega_n^k$(当 $n$ 为偶数)
- 折半引理:$(\omega_n^k)^2 = \omega_{\frac{n}{2}}^k$(当 $n$ 为偶数)
FFT 的分治思想
FFT 的核心思想是分治。假设我们要对一个 $n-1$ 次多项式 $A(x) = \sum_{i=0}^{n-1} a_i x^i$ 在 $n$ 个单位根 $\omega_n^0, \dots, \omega_n^{n-1}$ 上求值(这里假定 $n$ 是 2 的幂,不足则高位补 0)。
我们将 $A(x)$ 按系数的奇偶性分成两部分:
$$ \begin{align*} A(x) & = (a_0 + a_2x^2 + \dots) + (a_1x + a_3x^3 + \dots)\ & = x(a_1 + a_3x^2 + \dots) + (a_0 + a_2x^2 + \dots) \end{align*} $$
令 $A_0(y) = a_0 + a_2y + a_4y^2 + \dots, A_1(y) = a_1 + a_3y + a_5y^2 + \dots$
则有
$$ A(x) = A_0(x^2) + x A_1(x^2) $$
现在,我们要在 $x = \omega_n^k$ 处求值:
$$ A(\omega_n^k) = A_0((\omega_n^k)^2) + \omega_n^k A_1((\omega_n^k)^2) $$
利用折半引理 $(\omega_n^k)^2 = \omega_{\frac{n}{2}}^k$,上式变为:
$$ A(\omega_n^k) = A_0(\omega_{\frac{n}{2}}^k) + \omega_n^k A_1(\omega_{\frac{n}{2}}^k) $$
对于 $k+\frac{n}{2}$ 的情况:
$$ A(\omega_n^{k+\frac{n}{2}}) = A_0(\omega_{\frac{n}{2}}^{k+\frac{n}{2}}) + \omega_n^{k+\frac{n}{2}} A_1(\omega_{\frac{n}{2}}^{k+\frac{n}{2}}) $$
利用周期性和对称性 $\omega_{\frac{n}{2}}^{k+\frac{n}{2}} = \omega_{\frac{n}{2}}^k$ 和 $\omega_n^{k+\frac{n}{2}} = -\omega_n^k$,上式变为:
$$ A(\omega_n^{k+\frac{n}{2}}) = A_0(\omega_{\frac{n}{2}}^k) - \omega_n^k A_1(\omega_{\frac{n}{2}}^k) $$
我们发现,计算 $A(\omega_n^k)$ 和 $A(\omega_n^{k+\frac{n}{2}})$ 所需的子问题 $A_0(\omega_{\frac{n}{2}}^k)$ 和 $A_1(\omega_{\frac{n}{2}}^k)$ 是完全相同的!
这意味着,一个规模为 $n$ 的问题,可以被分解为两个规模为 $\frac{n}{2}$ 的子问题,外加 $O(n)$ 的合并操作。这正是分治法的结构。其时间复杂度为:
$$ T(n) = 2T(\frac{n}{2}) + O(n) = O(n \log n) $$
逆变换(IFFT)
求值过程(也称为离散傅里叶变换,DFT)的逆过程——插值,可以通过逆离散傅里叶变换(IDFT)完成。可以证明,IDFT 的计算过程与 DFT 惊人地相似。
如果一个序列 $\set{y_0, \dots, y_{n-1}}$ 是序列 $\set{a_0, \dots, a_{n-1}}$ 的 DFT,那么:
$$ a_k = \frac{1}{n} \sum_{j=0}^{n-1} y_j (\omega_n^{-k})^j $$
这表明,IDFT 除了主元(单位根)从 $\omega_n^k$ 变成了它的共轭复数 $\omega_n^{-k}$,并且最后结果需要除以 $n$ 之外,其余计算过程和 DFT 完全一样。因此,我们可以复用 FFT 的代码来实现 IFFT。
模板题
快速数论变换(NTT)
FFT 虽然快,但有一个致命弱点:浮点数精度误差。在处理系数很大或者需要取模的题目时,FFT 会因为精度问题得到错误答案。
快速数论变换(Number Theoretic Transform, NTT)是 FFT 在模数域上的变种,它使用原根替代单位根,从而在整数环内完成变换,完全避免了精度问题。
- 原根:在一个模 $p$ 的整数环中,如果一个整数 $g$ 满足 $g^k \pmod{p}$($k=1, \dots, p-1$)的结果互不相同,则称 $g$ 是模 $p$ 的一个原根。
- NTT 的条件:NTT 的存在需要模数 $p$ 是一个质数,且 $p-1$ 必须是 $N$ 的倍数,其中 $N$ 是变换的长度(通常是 2 的幂)。即 $p = k \cdot N + 1$ 的形式。
- NTT 中的“单位根”:我们取 $g^{(p-1)/N} \pmod{p}$ 作为 $N$ 次“单位根” $\omega_N$。可以证明,它在模 $p$ 意义下拥有和复数单位根完全相同的性质,从而可以执行与 FFT 相同的分治算法。
常用的 NTT 模数:
$$ 998244353 = 119 \cdot 2^{23} + 1 \text{(原根为 3)} \ 1004535809 = 479 \cdot 2^{21} + 1 \text{(原根为 3)} \ 469762049 = 7 \cdot 2^{26} + 1 \text{(原根为 3)} $$
NTT 的代码实现与 FFT 非常相似,只需将复数运算替换为模意义下的整数运算即可。
生成函数
生成函数(Generating Function),又称母函数,是组合数学中一个强大的工具。它将一个无限序列 $\set{a_0, a_1, a_2, \dots}$ 与一个函数(形式幂级数)关联起来,通过对函数进行代数运算,来解决序列相关的问题(通常是计数问题)。
普通生成函数(OGF)
对于序列 $A = [a_0, a_1, a_2, \dots]$,其普通生成函数(Ordinary Generating Function, OGF)定义为:
$$ F(x) = \sum_{n=0}^{\infty} a_n x^n $$
这里的 $x$ 是一个形式变量,我们只关心它的系数。
基本例子:
- 序列 $[1, 1, 1, \dots]$ 的 OGF 是 $F(x) = \sum_{n=0}^{\infty} x^n = \frac{1}{1-x}$。
- 序列 $[1, c, c^2, c^3, \dots]$ 的 OGF 是 $F(x) = \sum_{n=0}^{\infty} (cx)^n = \frac{1}{1-cx}$。
- 有限序列 $[1, 1, \dots, 1]$(共 $m+1$ 项)的 OGF 是 $F(x) = \sum_{n=0}^{m} x^n = \frac{1-x^{m+1}}{1-x}$。
核心思想:生成函数的强大之处在于,组合问题的“相加”和“相乘”规则,可以对应到生成函数的“相加”和“相乘”运算上。
- 加法法则:如果一个问题可以分为互斥的 A 和 B 两类,那么总方案数的生成函数等于 A 类方案的生成函数与 B 类方案的生成函数之和。
- 乘法法则:如果一个问题可以分为独立的 A 和 B 两个步骤,总方案数的生成函数等于 A 步骤方案的生成函数与 B 步骤方案的生成函数之积。
应用举例:背包问题。假设有两类物品,第一类物品的体积为 2,有无限件;第二类物品的体积为 3,有无限件。问装满容量为 $n$ 的背包有多少种方案?
- 第一类物品的生成函数(体积作为 $x$ 的指数):$A(x) = 1 + x^2 + x^4 + \dots = \frac{1}{1-x^2}$
- 第二类物品的生成函数:$B(x) = 1 + x^3 + x^6 + \dots = \frac{1}{1-x^3}$
根据乘法法则,总方案的生成函数为:
$$ C(x) = A(x)B(x) = \frac{1}{1-x^2} \frac{1}{1-x^3} $$
$C(x)$ 展开后 $x^n$ 的系数,就是装满容量为 $n$ 的背包的方案数。这个系数可以通过多项式求逆等操作(依赖于 NTT)来求得。
斐波那契数列的生成函数
OIwiki 上这一节的推导是错的。
斐波那契数列定义为 $f_0=1, f_1=1, f_n = f_{n-1} + f_{n-2}$。
令其生成函数为 $F(x) = \sum_{n=0}^{\infty} f_n x^n$。根据递推关系:
$$ \begin{align*} F(x) & = f_0 + f_1 x + f_2 x^2 + \cdots \ xF(x) & = f_0x + f_1 x^2 + f_2 x^3 + \cdots \ x^2F(x) & = f_0x^2 + f_1 x^3 + f_2 x^4 + \cdots \ \end{align*} $$
三式相减得到: $$ (1-x-x^2)F(x) = f_0 + f_1 x - f_0 x = 1 $$ 解出 $$ F(x) = \frac{1}{1-x-x^2} $$

