EagleBear2002 的博客

这里必须根绝一切犹豫，这里任何怯懦都无济于事

数据库系统概论-06-关系数据理论

发表于 更新于 分类于 ，
本文字数： 2.9k 阅读时长 ≈ 3 分钟

关系模式及范式

关系模式由五部分组成，是一个五元组： $R(U, D, \textup{DOM}, F)$

  1. 关系名 $R$ 是符号化的元组语义
  2. $U$ 为一组属性
  3. $D$ 为属性组 $U$ 中的属性所来自的域
  4. $\textup{DOM}$ 为属性到域的映射
  5. $F$ 为属性组 $U$ 上的一组数据依赖

由于 $D$、$\textup{DOM}$ 与模式设计关系不大，因此可以把关系模式看作一个三元组：$R \langle U, F \rangle $

作为二维表，关系要符合一个最基本的条件：每个分量必须是不可分开的数据项。满足了这个条件的关系模式就属于第一范式（1NF）。

数据依赖的主要类型：

  1. 函数依赖（Functional Dependency，简记为 FD）
  2. 多值依赖（Multi-Valued Dependency，简记为 MVD）

范式是符合某一种级别的关系模式的集合。关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式。

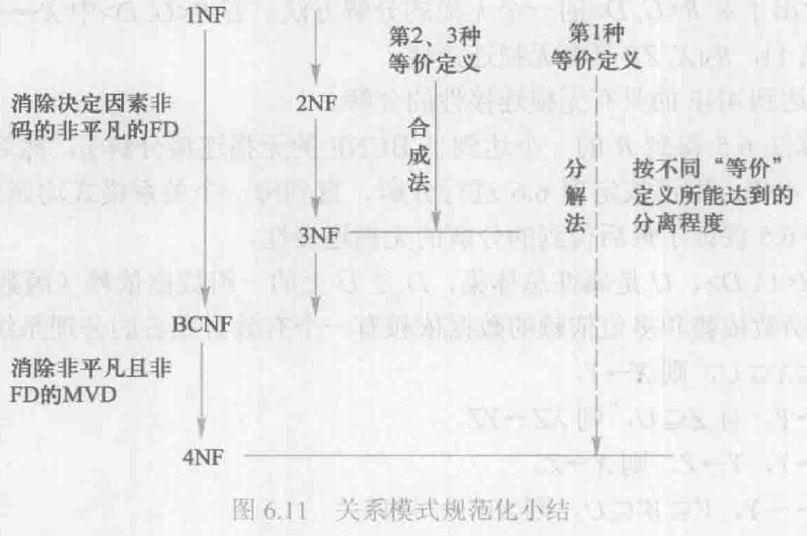
各种范式之间存在联系： $1NF \supset 2NF \supset 3NF \supset BCNF \supset 4NF \supset 5NF$。

一个低一级范式的关系模式，通过模式分解（schema decomposition）可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化（normalization）。

函数依赖

设 $R(U)$ 是一个属性集 $U$ 上的关系模式，$X$ 和 $Y$ 是 $U$ 的子集。若对于 $R(U)$ 的任意一个可能的关系 $r$，$r$ 中不可能存在两个元组在 $X$ 上的属性值相等，而在 $Y$ 上的属性值不等，则称“$X$ 函数确定 $Y$”或“$Y$ 函数依赖于 $X$”，记作 $X \to Y$，$X$ 称为这个函数依赖的决定因素（Determinant）。函数依赖是语义范畴的概念。只能根据数据的语义来确定函数依赖。

在关系模式 $R(U)$ 中，对于 $U$ 的子集 $X$ 和 $Y$：

  1. 如果 $X \to Y$，但 $Y \nsubseteq X$，则称 $X \to Y$ 是非平凡的函数依赖。
  2. 若 $X \to Y$，但 $Y \subseteq X$, 则称 $X \to Y$ 是平凡的函数依赖。

对于任一关系模式，平凡函数依赖都是必然成立的，它不反映新的语义，因此若不特别声明，我们总是讨论非平凡函数依赖。

在 $R(U)$ 中，如果 $X \to Y$，并且对于 $X$ 的任何一个真子集 $X’$, 都有 $X’ \nrightarrow Y$，则称 $Y$ 对 $X$ 完全函数依赖，记作 $X \overset{F}\to Y$。若 $X \to Y$，但 $Y$ 不完全函数依赖于 $X$，则称 $Y$ 对 $X$ 部分函数依赖，记作 $X \overset{P}\to Y$。

在 $R(U)$ 中，如果 $X \to Y(Y \nsubseteq X)$，$Y \nrightarrow X$， $Y \to Z$，$Z \nsubseteq Y$，则称 $Z$ 对 $X$ 传递函数依赖（transitive functional dependency）。记为 $X \overset{传递}\longrightarrow Z$。

设 $K$ 为 $R \langle U,F \rangle$ 中的属性或属性组合。若 $K \overset{F}{\to} U$，则 $K$ 称为 $R$ 的一个候选码（Candidate Key）。如果 $U$ 函数依赖于 $K$，即 $K \to U$，则 $K$ 称为超码（Surpkey）。候选码是一类特殊的超码，即候选码的超集（如果存在）一定是超码，候选码的任意一个真子集都不是超码。（课件此处有误，以本文档内容为准）

课程幻灯片 ch33-函数依赖与码 中 码 1 这一页对超码的定义存在逻辑矛盾：

在《数据库系统概论（第五版）》（2014 年 9 月第 1 次印刷，以下简称 14 版）中对超码的定义如下：

而在《数据库系统概论（第五版）》（2021 年 11 月第 21 次印刷，以下简称 21 版）中对超码的定义如下：

课程幻灯片中定义与 14 版定义相同，与 21 版定义相左。

14 版定义中存在逻辑问题：$U$ 完全函数依赖于候选码，$U$ 部分函数依赖于超码，那么候选码就不可能是最小的超码，因为完全函数依赖和部分函数依赖是互斥关系。

21 版定义逻辑自洽，因此我认为课程幻灯片不应采用 14 版定义，而应采用 21 版定义。

勘误地址（Moodle 访问）：http://219.219.120.72/mod/forum/view.php?id=7066

关系模式 $R$ 中属性或属性组 $X$ 并非 $R$ 的码，但 $X$ 是另一个关系模式的码，则称 $X$ 是 $R$ 的外部码（Foreign key）也称外码。

1NF

如果一个关系模式 $R$ 的所有属性都是不可分的基本数据项，则 $R \in 1NF$。

第一范式是对关系模式的最起码的要求。 不满足第一范式的数据库模式不能称为关系数据库。

2NF

若关系模式 $R \in 1NF$，并且每一个非主属性都完全函数依赖于任何一个候选码，则 $R \in 2NF$。

性质：不存在（某非主属性）部分依赖（于某一候选码）。

实例

下面是一个例子，该关系不是 2NF。其中 $Sno$ 是学号，$Cno$ 是课程号，$Sdept$ 是系别，$Sloc$ 是住所。虚线表示属性对候选码的部分函数依赖。

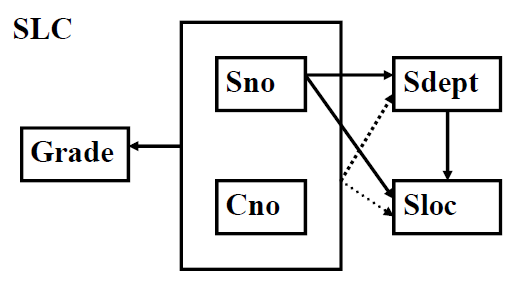
存在的问题

  1. 无法添加未选课的学生；
  2. 删除学生的最后一门课时，学生其他信息也被删除；
  3. 转系（同时还要转宿舍）修改成本高；
  4. 系别和住所信息多次存储。

解决方案

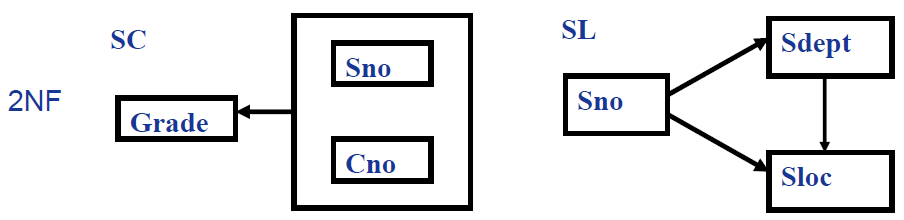
这一解决方案消除了问题 1、2 和 4。

3NF

设关系模式 $R\ \langle U,F\ \rangle \in 1NF$，若 $R$ 中不存在这样的码 $X$、属性组 $Y$ 及非主属性 $Z(Z \nsupseteq Y)$，使得 $X \to Y, Y \to Z$ 成立，$Y \nrightarrow X$ 不成立，则称 $R \langle U,F \rangle \in 3NF$。

性质：不存在（某非主属性）传递依赖、部分依赖（于某一候选码）

解决方案

在 2NF 的解决方案中，存在传递依赖 $Sno \to Sdept \to Sloc$。

解决方案为把 S-L 分解为 S-D 和 D-L。分解后的关系不再存在传递依赖，消除了问题 3。

BCNF

BCNF（Boyce Codd Normal Form）由 Boyce 和 Codd 提出，比 3NF 更进了一步。通常认为 BCNF 是修正的第三范式，有时也称为扩充的第三范式。

设关系模式 $R \langle U,F \rangle \in 1NF$，若 $X \to Y$ 且 $Y \nsubseteq X$ 时 $X$ 必含有码，则 $R \langle U,F \rangle \in BCNF$。换言之，在关系模式 $R \langle U,F \rangle $ 中，如果每一个决定属性集都包含候选码，则 $R \in BCNF$。

性质：

  1. 所有非主属性都完全函数依赖于每个候选码（2NF 性质）
  2. 所有主属性都完全函数依赖于每个不包含它的候选码（3NF 性质）
  3. 每一个决定属性集都包含候选码（亦即没有任何属性完全函数依赖于非码的任何一组属性）

一个模式中的关系模式如果都属于 BCNF，那么在函数依赖范畴内，它已实现了彻底的分离，已消除了插入和删除的异常。

实例

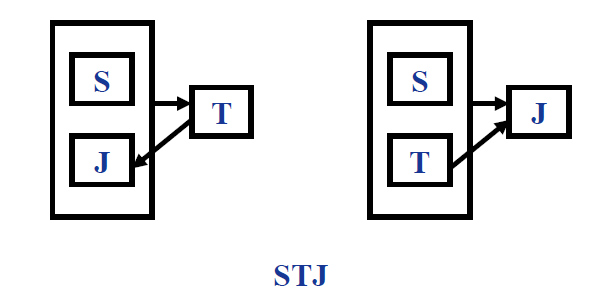
关系模式 $STJ(S,T,J)$ 中， $S$ 表示学生，$T$ 表示教师，$J$ 表示课程。每一教师只教一门课。每门课有若干教师，某一学生
选定某门课，就对应一个固定的教师。

左边的关系不满足 BCNF，右边的关系满足 BCNF。

小结