客户程序鲁棒性综述

摘要

数据库客户程序鲁棒性问题是数据库一致性领域的一个分支，是验证客户程序在弱隔离级别下的行为在多大程度上满足某个强隔离级别（一般是 SER）。鲁棒性常被分为动态鲁棒性和静态鲁棒性两个层次来讨论。

动态鲁棒性研究数据库的某一个弱隔离级别 $I_{1}$ 下的执行历史 $H$ 是否满足较强的隔离级别 $I_{2}$ （一般是 SER）。如果满足，我们说 $H$ 在 $I_{1}$ 下是鲁棒的。动态鲁棒性的研究与执行历史验证较为相似。
静态鲁棒性研究客户程序 $P$ 在弱隔离级别 $I_{1}$ 下的所有执行历史是否都满足较强的隔离级别 $I_{2}$ （一般是 SER）。如果满足，我们说 $P$ 在 $I_{1}$ 下是鲁棒的。例如，如果 $P$ 在 SI 下鲁棒，则我们可以在 SI 下运行 $P$ ，这可以在保证执行历史满足 SER 的情况下提高系统性能和吞吐率。

现有工作综述

$I_{1} ∖ I_{2}$	PC	SI	SER
RU			[Ketsman PODS'20] （非分布式）充要条件
RC			[Ketsman PODS'20] （非分布式）充要条件 [Vandevoort VLDB'21] （非分布式）事务模板的充要条件，有实验数据，未开源
RA
CC	[Bouajjani ESOP'21] 充要条件，转化为 CC 对 SER 鲁棒性	[Bouajjani ESOP'21] 充要条件， $C C \to P C \land P C \to S I$	[Bernardi CONCUR'16] 充分条件 [Beillahi CONCUR'19] CC、CM、CCv 下充要条件
PC	/	[Bouajjani ESOP'21] 充要条件，依赖程序搜索	[Bernardi CONCUR'16] 充分条件
PSI	/	[Cerone PODC'16] 充分条件	[Bernardi CONCUR'16] 充分条件
SI	/	/	[Fekete TODS'05] 充分条件 [Cerone PODC'16 & JACM'18] 充要条件 [Bernardi CONCUR'16] 充分条件

TODS2025 Allocating Isolation Levels to Transactions in a Multiversion Setting

problems

传统上，应用程序开发人员需要手动为每种类型的事务静态地选择一个隔离级别，这极具挑战性。如果选择过于保守的隔离级别（例如全部使用可串行化），会严重影响吞吐量；如果选择较低的隔离级别，则需要编写复杂的代码来处理可能出现的并发异常，这不仅容易出错，也增加了开发负担。

contributions

本文提出了一种在多版本数据库中系统性地分配隔离级别给事务的框架。其核心贡献在于，该框架能够根据事务的特性和行为，自动为每个事务动态地分配最合适的隔离级别，以在确保所需正确性的前提下最大化性能。它旨在将复杂性从应用程序开发人员转移到数据库系统内部。

techniques (basic ideas)

该框架的基本思想是，它通过分析事务的访问模式（读集和写集），动态地识别潜在的冲突。例如，对于只读事务，可以安全地分配快照隔离级别以实现高吞吐量；而对于可能产生写偏斜等异常的事务，系统会将其隔离级别自动提升到可串行化。该方法可能结合静态分析和运行时监控，以在事务执行前或执行期间做出明智的隔离级别决策。

limitations

该方法可能存在以下局限：

分析开销：在事务执行前进行复杂的访问模式分析可能会引入额外的开销。
无法处理所有动态情况：对于某些高度动态或依赖于运行时输入才能确定访问模式的事务，其分析的准确性可能会受限。
依赖于工作负载：该框架的性能增益可能高度依赖于数据库的工作负载，如果大部分事务都存在潜在冲突，则其优势会减弱。

arXiv2025 2501.18377v3 Using Read Promotion and Mixed Isolation Levels for Performant Yet Serializable Execution of Transaction Programs

problems

在实践中，许多数据库系统默认使用快照隔离（SI）等较低的隔离级别，以换取更高的性能。但这将处理并发异常（如写偏斜）的责任推给了应用程序开发者。目前的挑战在于，如何在不牺牲性能的前提下，为事务程序提供可串行化的正确性保证，从而简化开发。

contributions

本文提出了一种名为**“读提升”（Read Promotion）的新技术，并将其与混合隔离级别相结合。该方法的核心思想是，让事务在执行时以较低的隔离级别（如 SI）开始**，一旦系统检测到可能导致可串行化异常的特定条件，就会在运行时动态地将事务提升到更高的隔离级别。其结果是，应用程序获得了可串行化的保证，而系统则避免了在没有必要时使用开销巨大的高隔离级别。

techniques (basic ideas)

该技术基于一个两阶段模型：

初始阶段：所有事务都以快照隔离（SI）运行，该级别通常提供很好的并发性能。
动态提升：系统持续监控事务的读写依赖关系。例如，当一个事务 A 读取了另一个并发事务 B 刚刚写入的数据，而事务 A 自身又要写入数据时，存在写偏斜的潜在风险。一旦检测到这种模式，系统会立即执行**“读提升”**，将事务 A 的隔离级别提升到可串行化，从而防止异常的发生，并可能触发事务中止或锁升级。

limitations

该方法的局限性包括：

检测开销：运行时监控和检测潜在异常模式会引入额外的开销，特别是在高并发环境下。
提升时机：如果提升机制不够智能，可能导致过早或过晚的提升，从而影响性能。过晚的提升可能意味着事务已经进行了大量工作，然后才被中止。
不透明性：对于应用程序开发者来说，事务何时被提升是不透明的，这可能使得调试变得更加困难。

VLDB2025 TxnSails-Achieving Serializable Transaction Scheduling with Self-Adaptive Isolation Level Selection

problems

如何构建一个能够自动、持续地为每个事务选择最佳隔离级别的调度器，同时保证整个事务执行序列的可串行化，是一个重要的挑战。这需要系统能够理解不同事务类型的行为，并随着工作负载的变化而动态调整。

contributions

本文提出了一个名为 TxnSails 的自适应事务调度框架。其核心贡献在于，它引入了一种基于学习和反馈机制的隔离级别自适应选择器。该系统能够观察事务执行历史，学习不同事务类型在不同隔离级别下的表现（例如，冲突率、延迟），并据此为新来的事务动态地选择最合适的隔离级别，从而在不牺牲可串行化正确性的前提下最大化系统吞吐量。

techniques (basic ideas)

TxnSails 的基本思想是**“自适应学习”。它通过一个内部模型，持续收集并分析事务执行的元数据（如读写集、事务持续时间、冲突类型）。该模型将这些数据作为输入，输出一个策略，决定在当前工作负载下，哪种隔离级别最适合哪种事务类型。例如，对于历史上很少引发冲突的事务类型，调度器可能会为其分配快照隔离；而对于经常导致写偏斜的事务类型，调度器则会为其默认分配可串行化。这个模型是持续更新**的，能够随着工作负载的变化而自我调整。

limitations

该框架的局限性包括：

“冷启动”问题：在系统刚启动或工作负载发生剧烈变化时，学习模型可能需要一段时间来积累足够的数据才能做出有效的决策，这期间性能可能不如预期。
模型开销：收集数据和运行自适应模型本身会产生额外的计算和存储开销。
调试挑战：由于隔离级别的选择是自动化且动态的，当出现问题时，很难追溯和解释系统为何做出了某个特定的决策，这给调试和维护带来了挑战

Gotsman 等人在 Robustness 上的贡献

CONCUR'16-Robustness against Consistency Models with Atomic Visibility
- 给出 CC、PC、PSI、SI 下静态鲁棒性的充分条件
PODC'16-Analysing Snapshot Isolation & JACM'18-Analysing Snapshot Isolation（更长）
- 用集合不等式定义 SI，似乎是基于 Kleene Algebra with Tests [Kozen CSL'96]
- 对 SI 下的事务斩断进行静态分析
- 给出鲁棒性 SI $\to$ SER 和 PSI $\to$ SI 的充要条件，但过于简略且未给出算法
- 整篇文章完全基于数学分析，没有原型工具和实验
CONCUR'17-Algebraic Laws for Weak Consistency
- 揭示了抽象执行和依赖图两种形式化模型的内在联系

Beillahi 等人在 Robustness 上的贡献

CONCUR'19-Robustness Against Transactional Causal Consistency
- 给出 CC、CCv、CM（CC 的几个变体）下鲁棒性的充分条件
CAV'19-Checking Robustness Against Snapshot Isolation
ESOP'21-Checking Robustness Between Weak Transactional Consistency Models
- 验证了 CC-PC-SI-SER 四种隔离级别间的鲁棒性（除了 PC-SER）
- 将这些问题归结为可序列化下的状态可达性问题，在多项式时间内解决
- 目前唯一一个开源的工具：Boogie

Vandevoort 等人在 Robustness against RC 上的贡献

PODS'20-Deciding Robustness for Lower SQL Isolation Levels
- 理论细节最完善，是后续工作的基础；
- 提出了判定事务集合 $T$ 在无隔离级别、RU、RC 下鲁棒性的充要条件
VLDB'21-Robustness Against Read Committed for Transaction Templates
- 提出了判定事务集合 $T$ 和事务模板 $P$ 在 RC 下鲁棒性的充要条件和多项式时间算法
- 给出了 SmallBank 和 TPC-Ckv 的鲁棒子集
- 有实验数据，未开源
PODS'22-Robustness Against Read Committed-A Free Transactional Lunch
- 引入干涉图（interference graph）用于解释 VLDB'21 提出的算法，但并未给出证明
- 无实验数据
ICDT'22-Robustness Against Read Committed for Transaction Templates with Functional Constraints
- 对事务模板扩展了功能约束（functional constraints），看不懂
- 纯数学分析，无原型工具和实验
EDBT'23-Detecting Robustness against MVRC for Transaction Programs with Predicate Reads
- 扩展了具有控制结构（循环和条件）以及插入、删除和谓词读取的事务程序
- 有新算法和实验，未开源
SIGMOD'23-When is it safe to run a transactional workload under Read Committed
- 对以上所有文章的综述

数据库程序鲁棒性 benchamark

CAV'19-Checking Robustness Against Snapshot Isolation 使用了较多的 benchmark。

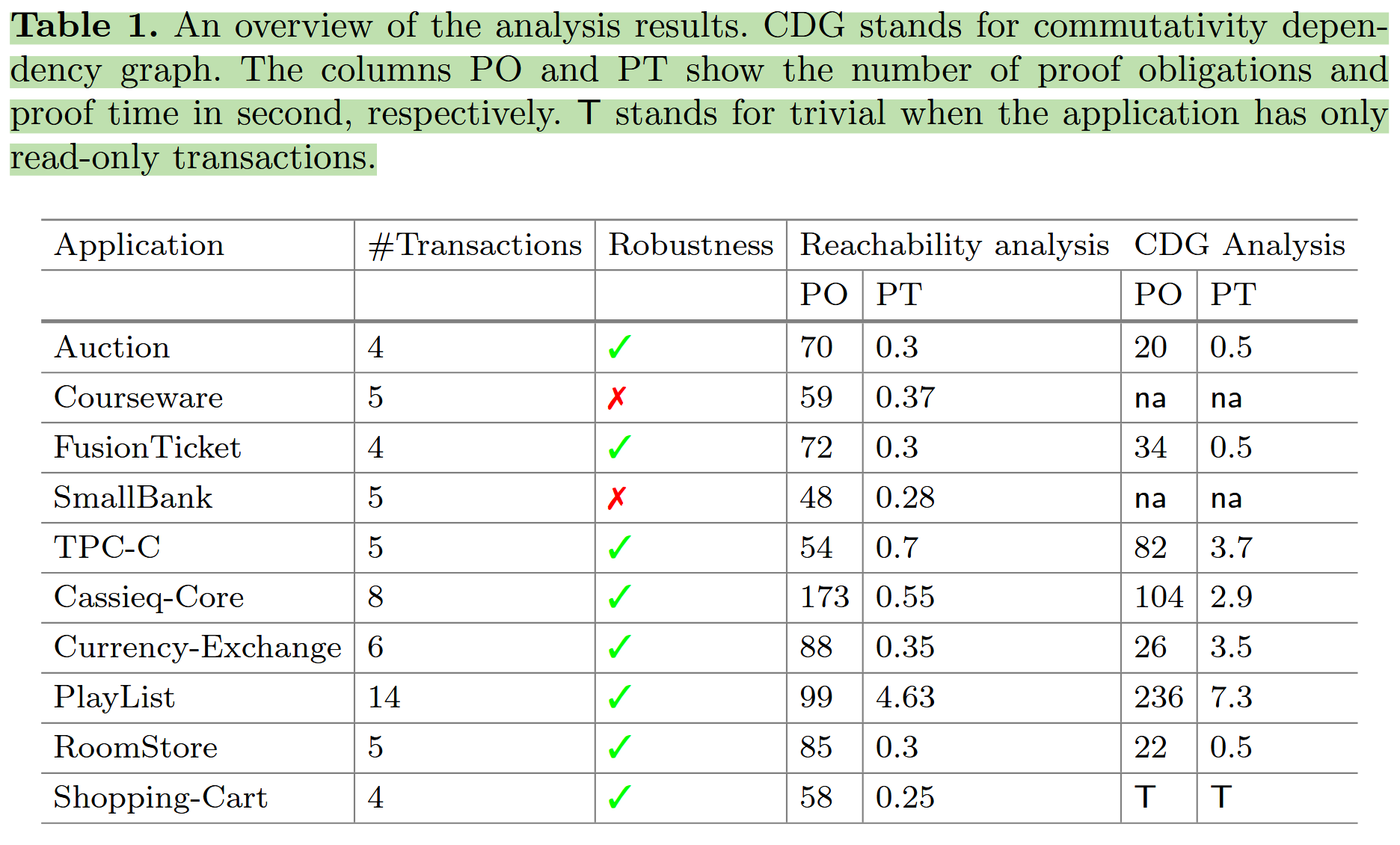
ESOP'21-Checking Robustness Between Weak Transactional Consistency Models

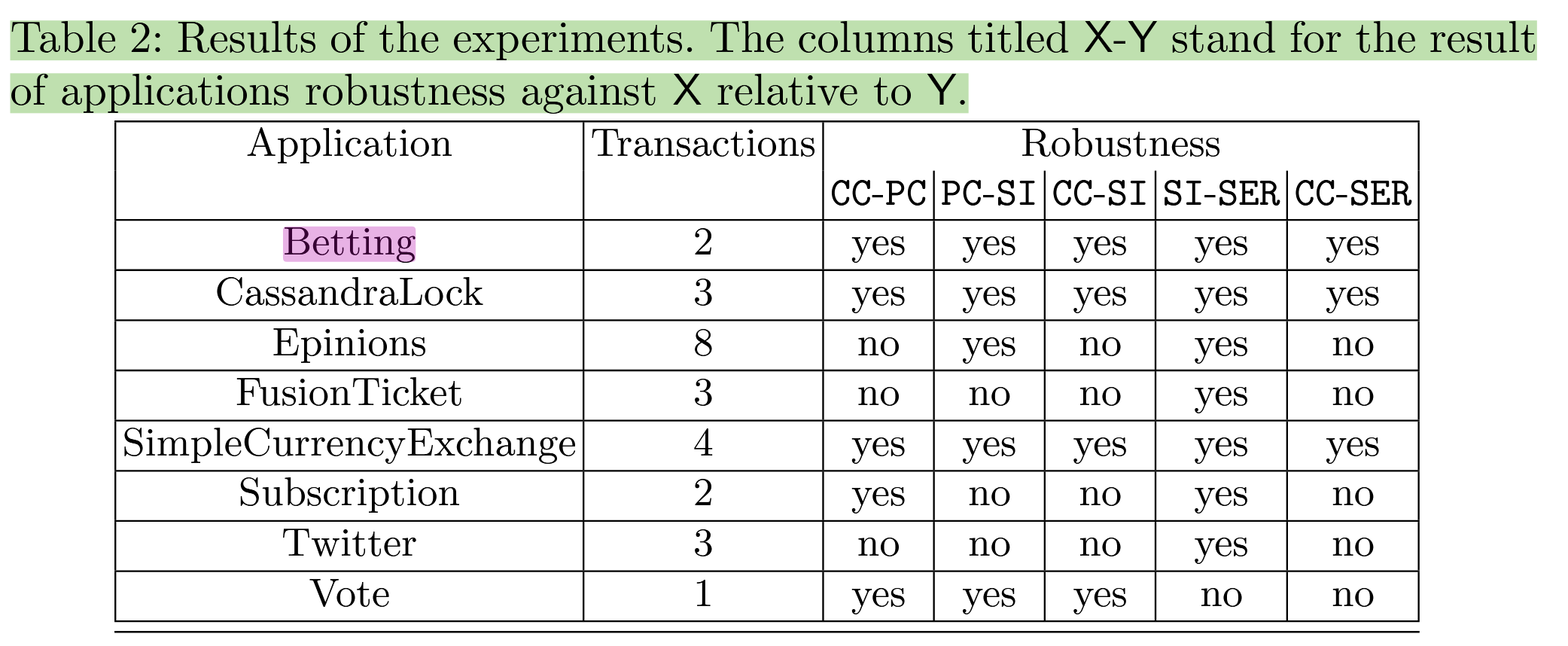
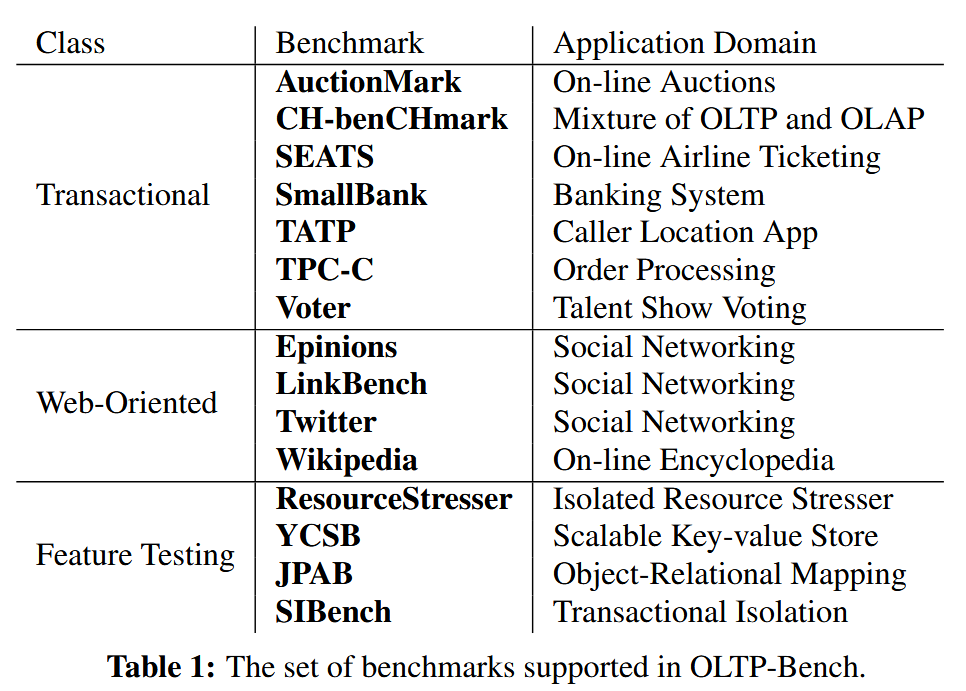
VLDB'14-OLTP-Bench an extensible testbed for benchmarking relational databases

EagleBear2002 的博客

客户程序鲁棒性综述

现有工作综述

TODS2025 Allocating Isolation Levels to Transactions in a Multiversion Setting

problems

contributions

techniques (basic ideas)

limitations

arXiv2025 2501.18377v3 Using Read Promotion and Mixed Isolation Levels for Performant Yet Serializable Execution of Transaction Programs

problems

contributions

techniques (basic ideas)

limitations

VLDB2025 TxnSails-Achieving Serializable Transaction Scheduling with Self-Adaptive Isolation Level Selection

problems

contributions

techniques (basic ideas)

limitations

Gotsman 等人在 Robustness 上的贡献

Beillahi 等人在 Robustness 上的贡献

Vandevoort 等人在 Robustness against RC 上的贡献

数据库程序鲁棒性 benchamark

混合隔离级别下鲁棒性