$$ \def\rd{\textcolor{orange}{\overset{rd}\Longrightarrow}} \def\b{\textcolor{green}{\overset{b}\rightsquigarrow}} \def\rf{\mathsf{\textcolor{green}{rf}}} \def\co{\mathsf{\textcolor{orange}{co}}} \def\fr{\textcolor{purple}{fr}} \def\br{\textcolor{purple}{br}} \def\po{\mathsf{\textcolor{red}{po}}} \def\porf{\po\rf} \def\init{\mathsf{init}} \def\next{\mathsf{next}} \def\Event{\mathsf{Event}} \def\R{\mathsf{R}} \def\W{\mathsf{W}} \def\Previous{\mathsf{Previous}} $$
摘要
动态偏序约简(DPOR)通过探索并发程序的所有交错直至某种等价关系(例如 Mazurkiewicz 迹等价)来验证并发程序。这样做涉及空间和时间之间的复杂权衡。现有的 DPOR 算法要么是探索最优的(即仅精确探索每个等价类的交错),但可能使用程序大小的指数内存,要么保持多项式内存消耗,但可能会探索指数级的许多冗余交错。
在本文中,我们表明可以两全其美:在线性内存消耗的情况下探索每个等价类的确切一个交错。我们的算法 TruSt 在 Coq 中形式化,不仅适用于顺序一致性,还适用于满足一些基本假设的任何弱内存模型,包括 TSO、PSO 和 RC11。此外,TruSt 的可并行性令人尴尬:它的不同探索选项没有共享状态,因此可以完全并行探索。因此,TruSt 在内存和/或时间方面优于最先进的技术。
作者:
- Michalis Kokologiannakis, MPI-SWS, Germany
- Iason Marmanis, MPI-SWS, Germany
- Vladimir Gladstein, MPI-SWS, Germany and St Petersburg University/JetBrains Research, Russia
- Viktor Vafeiadis, MPI-SWS, Germany
相关文章:https://zhuanlan.zhihu.com/p/446927002
INTRODUCTION
无状态模型检查(SMC)[Godefroid 1997; Musuvathi et al. 2008] 是一种用于验证有限尺寸的并发程序的有效验证技术。它是作为显式状态模型检查的替代方案而引入的,可以避免过多的内存消耗,因此有可能扩展到更大的程序。SMC 的工作原理是系统地探索给定并发程序的所有执行,而不存储它已经访问过的程序状态集。
虽然 SMC 允许根据多项式内存要求来验证程序,但它有一个明显的缺点,即要探索的执行次数通常与程序大小成指数关系。因此,SMC 几乎总是与巧妙的动态偏序约简(DPOR)算法一起使用 [Abdulla et al. 2014; Flanagan et al. 2005; Kokologiannakis et al. 2019] 减少了需要探索的执行次数,以覆盖所有可能的程序行为。DPOR 将程序的执行跟踪根据某些关系分为等效类,例如 Mazurkiewicz 跟踪等价 [Mazurkiewicz 1987],所有等效路径都表现出相同的可观察结果。然后,为了验证程序,只需从每个等价类中探索一条路径就足够了。
然而,探索每个等价类的一个代表性执行轨迹(即最优)并不容易。 DPOR 算法(例如,[Abdulla et al 2015; 2014; 2016; Albert et al 2017; 2018; Chalupa et al 2017; Chatterjee et al 2019; Flanagan et al 2005; Kokologiannakis et al 2019; Zhang et al 2015])通常开始通过探索一个程序路径,每当他们检测到一对竞争的的访问时,他们就会以相反的顺序探索包含竞争的访问的其他跟踪,同时还保持某种状态以避免重新探索等效的执行跟踪。然而,现有算法要么不是最优的,这意味着即使对于具有 $O(n)$ 等价类(其中 $n$ 是程序的大小)的程序,它们也可能探索指数数量的跟踪,或者通过牺牲 SMC 的发明来实现最优性多项式内存消耗。事实上,大多数现代 DPOR 验证问题解决方案都选择第二种解决方案,即它们可能会消耗指数级的内存。
在本文中,我们表明这种妥协是不必要的。我们开发了一种具有线性内存需求的探索最优 DPOR 算法。除了在时间和内存方面为 DPOR 提供可扩展的解决方案外,我们的算法,TruSt(Truly Stateless Model-checker)还具有另外两个大优势:
- 这两项内容是参数化的:(1) 内存模型的选择,不仅支持顺序一致性 (SC) [Lamport 1979],还支持各种弱内存模型,例如 TSO [Sewell et al 2010]、PSO [SPARC International Inc. 1994] 和 RC11 [Lahav et al 2017],以及 (2) DPOR 等价关系的选择,支持 Shasha-Snir 等价 [Shasha et al 1988](Mazurkiewicz 等价于弱内存模型)和读取等效性 [Chalupa et al 2017]。
- 它对不同执行跟踪的探索绝对不共享任何状态,这意味着 TruSt 的并行性令人尴尬。这与现有的 DPOR 解决方案形成鲜明对比,后者的并行化需要共享以避免重复(例如,[Lång et al 2020])。
为了实现这一目标,我们以之前的工作为基础——尤其是 GenMC [Kokologiannakis et al 2019]——并将程序执行表示为执行图 [Alglave et al 2014]。然而,我们从根本上改变了 DPOR 逆转恶意访问的条件。具体来说,我们限制只有当要删除的事件形成剩余执行的最大扩展时才发生反转——这是我们在本文中引入的一个新颖概念。我们证明最大扩展总是存在并且是唯一的,因此人们可以在不记录任何附加状态的情况下实现正确性和最优性。线性空间复杂度源于 TruSt 以递归深度优先的方式探索执行:递归深度受程序大小限制,每次递归调用都需要常数空间来表示其与当前执行图的差异,即大小也是线性的。
总之,我们做出以下贡献:
- $\S2$ 通过一系列示例,我们描述了现有 DPOR 解决方案的工作原理以及为什么保持最优性和多项式空间复杂性会带来相当大的挑战。
- $\S3$ 我们提供了一个直观的说明,说明 TruSt 如何通过将程序执行表示为图形并使用极大值概念限制替代探索来克服这一挑战。我们的算法适用于任何受一些基本假设限制的内存模型。
- $\S4$ 我们详细描述我们的算法,并证明(在 Coq 中)它是合理的、完整的和最优的。
- $\S5$ 我们将 TruSt 的并行版本实现为验证 C/C++ 程序的工具。
- $\S6$ 我们证明 TruSt 在内存和/或验证时间方面优于最先进的技术,并且它在多核机器上的扩展性非常好。
SMC & DPOR: A TROUBLED MARRIAGE
首先,为什么 SMC/DPOR 会遭受这种探索/内存权衡的困扰?为了回答这个问题,让我们首先回顾一下 DPOR 的基本原理。为了简化演示,在本节的其余部分中,我们假设顺序一致性(SC)的设置,并且使用的等价概念是 Mazurkiewicz 等价概念。在$\S 3$ 中,我们提出了这些假设并得出了 TruSt,这是一种与内存模型无关的 DPOR,它既适用于类似 Mazurkiewicz 的等价类,也适用于更粗略的等价划分。
DPOR in a Nutshell
正如简要提到的,DPOR 首先探索一个完整的程序交织,然后进入竞争检测阶段,当它识别出需要探索的进一步交织时。具体来说,它检测竞争的转换,如果以相反的顺序执行,将导致属于不同等价类的交错。然后,DPOR 以深度优先的方式一一探索这些替代方案。(在探索每个交错之后,运行竞争检测阶段,该阶段可以递归地生成要探索的进一步交错等等)
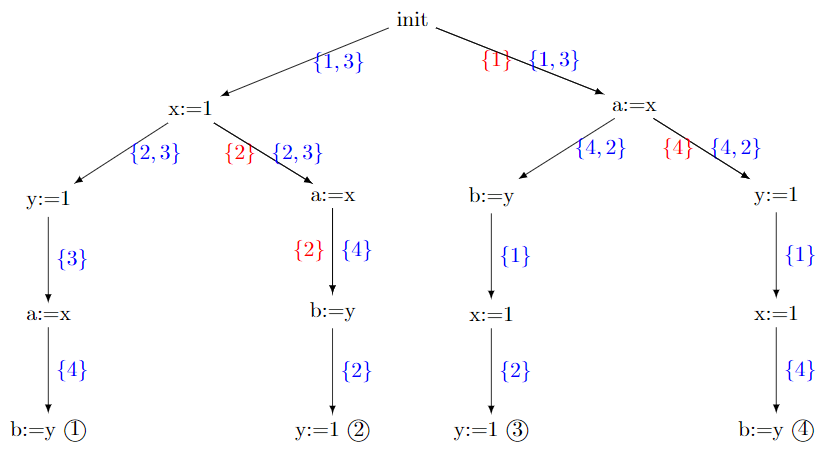
我们用下面的 $\mathsf{w+w+rr}$ 示例来说明上述过程,其中每条指令都被赋予了不同的标签。
$$ (1) x := 1 \parallel (2) y := 1 \parallel
\begin{array}{c} (3) a := x \ (4) b := y \ \end{array} $$
该程序有 12 个交错,分为 4 个 Mazurkiewicz 等价类。

TODO:上图中,红色的集合是睡眠集,蓝色的集合是每个转换的回溯集。
基本思想:交换竞争的转换(操作),以寻找新的路径
现在让我们看看 DPOR 如何生成该程序的所有四个 Mazurkiewicz 迹线。从空跟踪开始,DPOR 添加与程序转换相对应的事件,直到到达完整跟踪 ①,如图 1 所示。在此过程中,它会跟踪回溯集中每个步骤执行的转换,稍后它将记录任何替代探索选项。
一旦第一个跟踪被完全探索,DPOR 就会启动竞争检测($\rd$)阶段,并寻找竞争的转换。在 Mazurkiewicz 等价下,如果两个转换访问相同的内存位置,并且其中至少一个是写指令,则它们是竞争的。每当 DPOR 检测到两个竞争的转换时,它就会用另一个可用的转换填充较早转换的回溯集(backtrack set),这将迫使它以相反的顺序考虑竞争指令。
回到 $\mathsf{w+w+rr}$ 示例,有两对竞争的转换:$\langle 1, 3 \rangle$ 和 $\langle 2, 4 \rangle$。对于前一对,DPOR 使用 (3) 填充初始状态的回溯集,可以执行该回溯集而不是跟踪的第一次转换。然而,对于后一对竞争,请注意不能执行 (4) 来代替 (2),因为必须首先执行 (3)。因此, DPOR 使用 (3) 而不是 (4) 填充第二个转换的回溯集。(一般来说,当要记录在回溯集中的转换由于因果关系取决于某些先前的事件集而无法立即执行时,DPOR 会在回溯集中记录一些其他事件——通常但不一定是其中一个事件)。
现在竞争检测阶段已经完成,DPOR 以深度优先的方式考虑替代探索选项。它通过将跟踪限制为仅包含在该转换之前触发的事件,然后触发尚未探索的转换,来定位其回溯集中存在未探索的转换的最新转换,并回溯($\b$)。对于 $\mathsf{w+w+rr}$,第一个这样的转变是第二个,因此 DPOR 首先尝试扭转 (2) 和 (4) 之间的竞争。然而,要做到这一点,在竞争逆转之前(即,直到执行 (4) 之后),不应执行 (2)。 DPOR 通过将 (2) 放入睡眠集(sleep set)中来实现此目的,然后执行程序的其余转换(从 (3) 开始,如回溯集所示)。如图 1 所示,(2) 在执行 (4)(或者更一般地说,任何竞争的转换)时从睡眠集中删除。
此时,构建了第二个完整迹线(迹线 ②),并且 DPOR 再次启动竞争检测阶段。在此阶段中,检测到两个竞争:一个在转换 (1) 和 (3) 之间,一个在 (2) 和 (4) 之间。然而,这两个竞争都不会对后道设置产生任何影响。就第一个竞争而言,这几乎是预料之中的,因为 (3) 已经处于初始过渡的回溯组中。然而,也许令人惊讶的是,DPOR 也不会填充第三次转换的回溯集,尽管事实上 (2) 不属于那里的回溯集。原因是 (2) 处于该转换的睡眠集中。这表明这将“重新反转”正在反转的竞争(导致相当于迹线 ① 的跟踪),因此 DPOR 避免尝试一起反转第二个竞争。

随后,DPOR 进一步回溯(参见图 2)并探索第一次过渡的替代方案。由于已经探索了针对此转换触发 (1),因此将 (1) 插入睡眠集,并触发 (3)。此时,(1) 立即从睡眠集中移除,因为它正在与 (3) 进行竞赛。然后,DPOR 可以继续使用 (1)、(2) 和 (4) 中的任何一个,但我们假设它首先选择 (4),然后继续使用 (1) 和 (2),最终导致迹线 ③。
继续进行现在应该熟悉的竞争检测阶段,DPOR 注意到 (2) 与 (4) 处于数据竞争状态,因此将 (2) 插入第二个转换的回溯集中。
最后,算法回溯到第二个转换并触发 (2) 而不是 (4)。然后加上 (1) 和 (4) ,得到迹线 ④。与之前一样,④ 的竞争检测阶段不会向回溯集添加任何新的转换,从而结束了对该程序的所有四个不同 Mazurkiewicz 等价类的代表性交错的探索。
笔者将整个 DPOR 的搜索的过程用下图和伪代码表示。
2
3
4
5
6
7
8
9
10sleep_set;
traceback_set[];
procedure DPOR_DFS(u) {
find_valid_path();
race_detection();
}
procedure race_detection {
// add racy transitions into each traceback_set above
}
The Race-Reversal Problem
到目前为止,DPOR 有一个很大的缺点:竞争逆转的方式不是预先确定的。当 DPOR 检测到两个事件 a 和 b 之间存在竞争且 a 在跟踪中出现在 b 之前时,它需要填充在 a 位置设置的回溯集。然而,如果 b 在 a 的位置不可触发(例如,因为它因果上取决于 a 之后添加的一些其他事件,这里所说的因果取决于具体使用的 DPOR),则会添加一个不同的事件。事实上,我们已经看到了这个问题的一个例子:在 $\mathsf{w+w+rr}$ 的第一条踪迹的竞争检测阶段,(3) (而不是 (4))被添加到 (2) 的回溯集中,因为后者在那一点不可触发,因为它取决于转换 (3)。
一般来说,DPOR 使用出现在跟踪中 a 和 b 之间的事件 c 填充在 a 处设置的回溯,并且不因果依赖于任何其他事件。当然,虽然将 b 本身(或来自同一线程的 b 的前驱)添加到 a 的回溯集确实有意义,但这并不总是可能的,因为 b 可能依赖于跨越许多不同线程的多个其他事件。
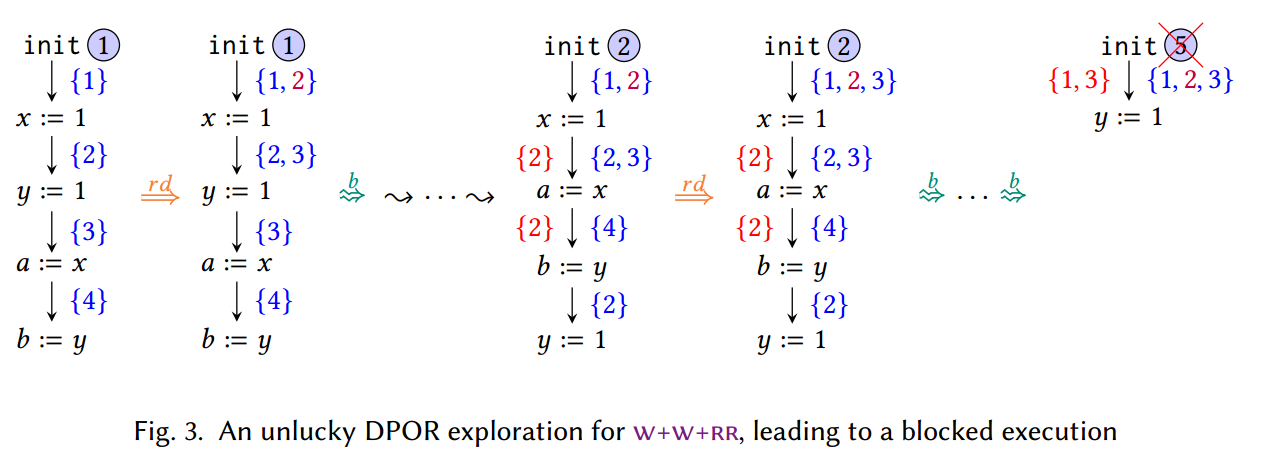
竞争逆转机制中的这种非确定性有时会导致 DPOR 遇到执行阻塞。要查看这样的示例,请再次考虑 $\S 2.1$ 中的 $\mathsf{w+w+rr}$ 示例,但这一次假设在迹线 ① 的竞争检测阶段,将 (2) 添加到第一个转换的回溯集中(而不是 (3)),如图 3 所示。在迹线 ② 的竞争检测过程中,DPOR 将发现与 $\S 2.1$ 探索中相同的竞争。然而,这一次有一个关键的区别:(1) 和 (3) 之间的竞争必须逆转。在 $\S 2.1$ 的运行中,(3) 已经位于第一个转换的回溯集中,因此在迹线 ② 的竞争检测阶段,DPOR 没有更改第一个转换的回溯集合。然而,在目前的探索中,(3) 并不属于第一次转变的回溯集。因此,DPOR 将其添加到此处,从而导致包含三个事件的回溯集。
TODO:在上一段的示例中,(2) 和 (1) 并不竞争,为什么要把 (2) 添加到第一个转换的回溯集中?
反过来,虽然对迹线 ②、③ 和 ④ 的探索与 $\S 2.1$ 中完全相同,但第一个转换的不同回溯集将导致无关的探索。事实上,如图 3 所示,DPOR 通过触发 (2) 作为第一个转换来开始探索。然而,所有其他可触发的转换都处于睡眠集中,这意味着这种无关的探索将被阻止。
更一般地说,即使在这个示例中,基本 DPOR 算法仅探索一个阻塞执行,但也存在具有线性数量的 Mazurkiewicz 等价类的参数程序,其中 DPOR 探索指数级的许多阻塞执行 [Abdulla et al 2017; Nguyen et al. 2018]。以最佳方式解决上述竞争逆转问题(即,仅探索每个 Mazurkiewicz 等价类的一条迹线)是非常困难的。而且,即使有 DPOR 算法能够实现这种最优性 [Abdulla et al 2017; 2019; 2018; Aronis et al. 2018; Kokologiannakis et al. 2019; 2020],正如我们很快就会看到的,所有此类解决方案都会遭受指数级的内存消耗。
Exponential-Cost Solutions to the Race-Reversal Problem
但现有的 DPOR 解决方案如何真正实现最优呢?这些技术背后的关键思想是不仅保存回溯集中的转换,而且保存转换序列。因此,每当 DPOR 试图逆转两个事件 a 和 b 之间的竞争(a 在跟踪中较早)时,它不必猜测应该将哪个转换添加到在 a 位置设置的回溯中;相反,它可以简单地添加一个包含 b 及其所有因果前身的序列,以便 a 和 b 之间的竞争精确逆转。通过这样做,它还可以摆脱睡眠集,该睡眠集仅用于不过早地触发转换(即在竞争逆转之前)。
作为一个具体的例子,让我们简要讨论 Abdulla 等人 [2014] 的最优 DPOR 算法的探索过程在验证 $\mathsf{w+w+rr}$ 示例时有何不同。在迹线 ① 的竞争检测阶段,最优 DPOR 将添加序列 3 和 3.4 以分别反转 (1) 和 (3) 以及 (2) 和 (4) 之间的竞争。通过这样做,optimal-DPOR 可以精确地逆转程序中的所有竞争,并且还可以避免探索任何阻塞的执行。
虽然保存转换序列足以保证最优性,但它可能导致指数内存消耗 [Abdulla et al 2014; Nguyen et al. 2018]。要查看这方面的示例,请考虑下面的 exp-mem 程序。
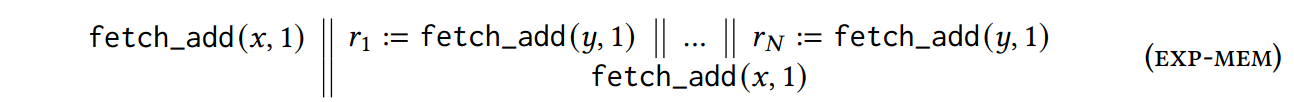
该程序的问题在于,指数数量的转换序列将存储在第一个 x 访问的回溯集中,并且只有在 y 访问上的所有竞争都反转后才会探索这些序列。具体地,假设最优 DPOR 算法通过按从左到右的顺序执行程序线程来获得程序的第一条踪迹。在该跟踪的竞争检测阶段,由于两个 x 访问之间的竞争,第一个 x 访问的回溯集将填充转换序列 s。由于第二次 x 访问因果关系取决于之前对 y 的所有访问,因此 s 将包含第一次访问 x 后触发的所有转换。
当然,s 的大小不是问题;然而,问题是 DPOR 还必须逆转 y 上的所有竞争。而且,更糟糕的是,对于每个反转,另一个(新的)转换序列将被插入到第一个 x 访问的回溯集中,因为它将与所有现有的 y 访问顺序不同。鉴于有 $N!$ 种 y 访问的排序方式,以及所有这些 $N!$ 在 x 上的竞争被逆转之前必须探索顺序(由于 DPOR 的类似 DFS 的性质),很明显,第一次 x 访问的回溯集将消耗指数量的内存。
TruSt: RECONCILING SMC & DPOR
在本节中,我们将描述 TruSt,这是我们的 DPOR 框架,它结合了三个关键功能:(1) 内存模型参数性、(2) 最优性和 (3) 多项式内存要求。在以下小节中,我们将逐步描述 TruSt 如何实现这些功能。为了避免混淆,我们对 TruSt 的每个“中间”版本使用不同的索引(即 TruSt~0~、TruSt~1~),直到我们在 $\S 3.5$ 中得到完整的算法。
TruSt~0~: Representing Executions as Graphs
使用执行图(execution graphs)而不是交错(interleavings)来表示执行。执行图本身是一个 DAG,包括 $\co, \rf, \le_G$ 分别对应数据库执行历史中的 WW、WR 和 Commit Order 关系。这一算法的优点是不需要为无竞争关系的事件确定相对顺序。
为了支持弱内存模型,我们不能简单地将程序执行表示为交错,因为我们必须考虑此类模型允许的可能的重新排序。因此,我们将并发程序的执行表示为执行图 [Alglave et al 2014],其中包含一组事件以及它们之间的一些关系。

我们对执行图的定义与文献中的大多数演示有两个不同之处。首先,它包含一个附加组件:总顺序 $\le_G$ ,TruSt 使用它来记录将事件添加到执行的顺序。其次,G 没有显式的程序顺序($\po$)组件。相反,$\po$ 是通过将事件表示为偏序来诱导的,该偏序根据同一线程的事件的序列号和所有非初始化事件之前的初始化事件进行排序。 $$ \po \triangleq \set{\langle \init, e\rangle | e \in \Event \setminus \set{\init}} \cup\left{\left\langle\left\langle t_{1}, i_{1}, l a b_{1}\right\rangle,\left\langle t_{2}, i_{2}, l a b_{2}\right\rangle\right\rangle \mid t_{1}=t_{2} \wedge i_{1}<i_{2}\right} $$
我们将因果依赖关系 $G.\porf$ 定义为程序顺序和读取依赖的传递闭包。
$$ G.\porf \triangleq(\po \cap(G . E \times G . E) \cup\set{\langle G . \rf(r), r\rangle \mid r \in G . R})^{+} $$
然后,程序 P 在内存模型 m 下的语义由满足 m 的一致性谓词的程序对应的执行图集合给出。一致性通常确保读取返回相对较新的值,并且写入的一致性顺序与程序顺序不矛盾。

作为示例,SC 下 $\mathsf{w+w+rr}$ 的一致执行图如图 4 所示。
在显示图表时,我们遵循弱内存文献中的标准约定,将 $\rf$ 函数绘制为虚线箭头,指示从写入到读取的数据流(而不是从每次读取到相应写入的功能映射)。类似地,我们仅将非传递 $\po$ 边绘制为实心黑色箭头,并隐式保留事件的 t 和 i 分量。最后,我们通常不会从初始化事件到其他写入绘制 $\co$ 边。
请注意,执行图包含 DPOR 使用的“等价类”概念。事实上,如图 4 所示,$\mathsf{w+w+rr}$ 在 SC 下有 4 个一致的执行图,尽管它有 12 个交错。尽管这些图引起的精确等价划分取决于内存模型定义和记录的关系,但请注意不同线程执行的操作在它们之间没有排序,并且默认情况下对不同变量的访问也是无序的。
TruSt 可以为任何满足三个基本假设的内存模型 $m$ 进行实例化:
- 格式良好(Well-formedness):一致性不取决于事件添加到图中的顺序(即,如果 $G$ 一致,则任何图 $G^{\prime} \approx G$ 也一致),并且,一致的图,$\po\rf$ 应该是无环的(即事件不能循环依赖于自身)。
- 前缀封闭性(Well-formedness):将一致图限制为其事件的任何 $\porf$-prefix-close 子集会产生得到的图也是一致的(即,若 G 是一致的,则 G 的任何前缀也是一致的)。前缀封闭性使 TruSt 能够增量地构建一致的图。
- 最大可扩展性(Maximal-extensibility:):如果以最大方式添加 $\po$-maximal 事件到一致图,则可以保持一致性:对于写入来说是 $\co$-maximally,对于读取来说是从 $\co$-maximally 写入中读取(关于 maximal 的定义,参考 $\S3.4$)。直观上,如果线程有更多语句要执行,则执行程序永远不会被卡住:其余语句始终可以使用 SC 语义执行(特别是,每次读取都可以返回由最近的同一位置写入写入的值)。
TruSt~0~: Partially Alleviating the Race-Reversal Problem
执行图使 TruSt~0~ 能够执行两项关键优化,这两项优化共同使其能够以最佳方式扭转超过 50% 的竞争。
第一个优化源于观察到 DPOR 的竞争检测阶段不需要在执行结束时发生,而是可以在每次将新事件添加到图中时增量执行。因此,每当将事件 b 添加到图中时,只需检查它是否与图中 G 中已有的某个事件 a 冲突即可。给定图形表示,这样的检查是非常自然的,因为如果 b 是写入或读取事件,TruSt~0~ 无论如何都必须确定 G 中的最后一个事件相同位置写入,以便分别更新 $\co$ 或 $\rf$ 组件。
第二个优化在逆转竞争时利用写入的语义:即,写入仅影响可以从内存读取的值,而不影响任何程序线程的本地状态。因此,如果我们在写入事件 a 和稍后的事件 b 之间存在竞争,我们不需要从执行图中删除任何事件。如果 b 是读事件,则改变 $G.\rf(b)$ 即可;而如果 b 是写入事件,则足以更改 a 和 b 之间的 $\co$ 边,同时保持其他事件不变。
下图中,紫色的集合是重访集。$\fr$ 是 forward revisit 的缩写。相比于基于交织的 DPOR,这一回溯的过程是:
- 不会删除两个活跃事件之间添加的任何事件;
- 从当前 R 事件的重访集修改对应的 $\rf$ 关系,使之从其他 W 那里读取。
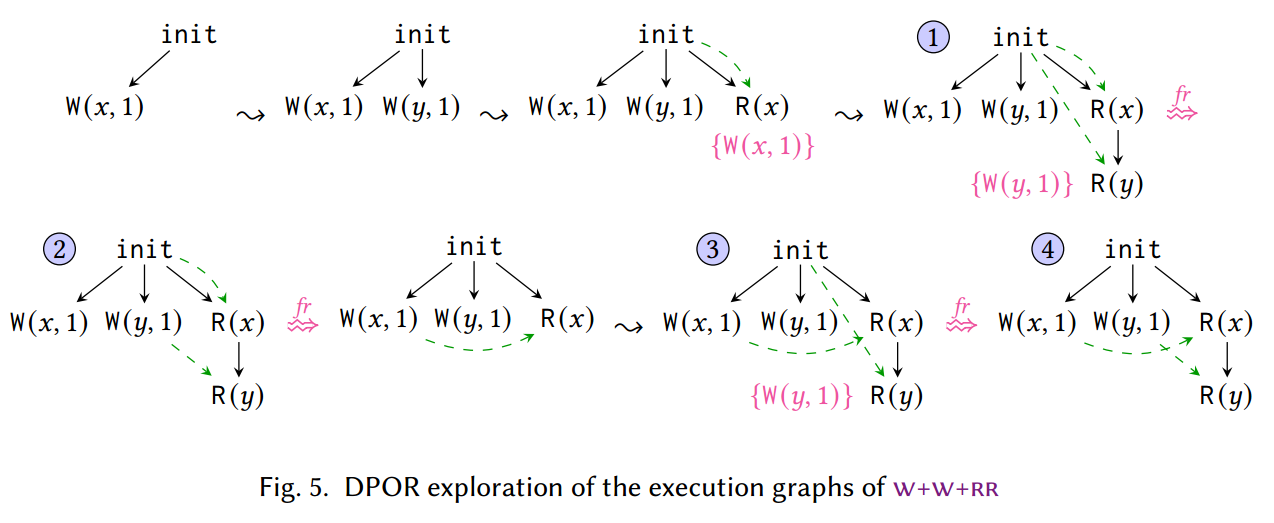
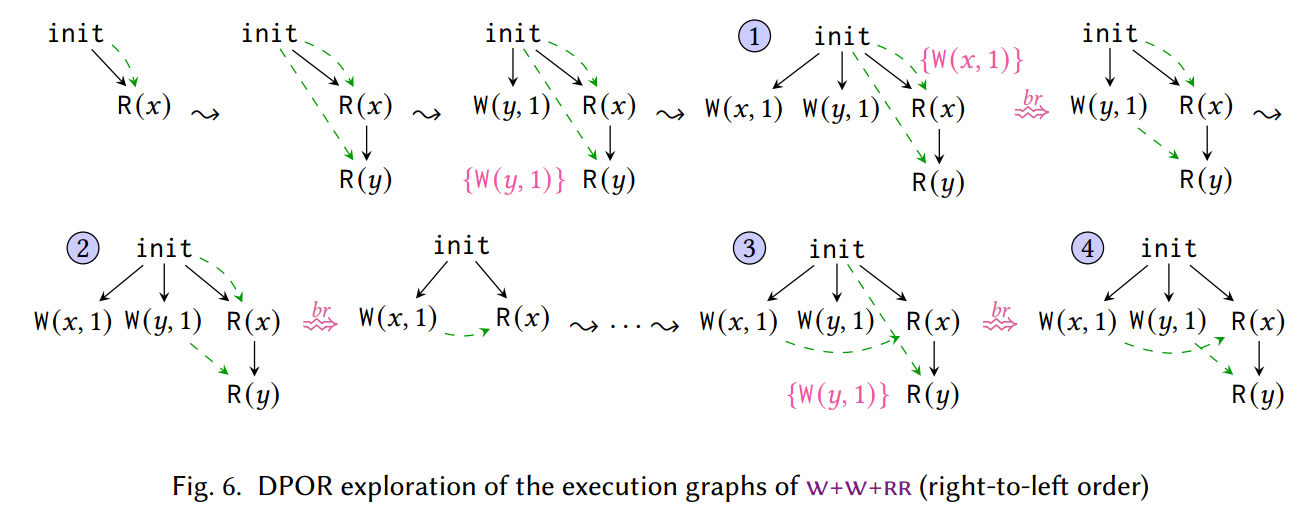
我们在 $\mathsf{w+w+rr}$ 示例中说明这些优化(参见图 5)。与基于交错的 DPOR 类似,TruSt~0~ 从初始图开始,并每次添加与程序指令相对应的事件。然而,与基于交错的 DPOR 相比,当 TruSt~0~ 添加读取事件时,其 $\rf$ 选项不限于单个写入;相反,它们是由内存模型的一致性谓词决定的。例如,当 TruSt~0~ 添加 $\R(x)$ 时,它无论读取 0 还是 1 都是一致的。因此,TruSt~0~ 继续处理一个 $\rf$ 选项(例如 0),并将另一个选项记录在与读取相关的重访集(revisit set)中。(重访集在某种程度上类似于 $\S 2$ 的回溯集,但请注意,它将替代选项与最后添加到图中的事件相关联)以类似的方式,当添加 $\R(y)$ 时,它将读取一个可能的值(例如,0),而任何替代方案(在本例中为 1)将被添加到其重新访问集中。
由于第一张图(图中 ①)已完成,TruSt~0~ 以深度优先的方式回溯并探索任何记录的替代选项。然而,TruSt~0~ 的回溯过程与基于交织的 DPOR 不同。当回溯以便 $\R(y)$ 从 $\W(y, 1)$ 读取时,TruSt~0~ 回溯到添加 $\R(y)$ 的点,而不是返回到初始状态(如基于交错的 DPOR 所做的那样),并简单地更改其 $\rf$ 以便从 $\W(y, 1)$,立即产生执行 ②。为了区分基于交织的 DPOR 和 TruSt~0~ 的回溯过程,我们将 TruSt~0~ 的回溯重访称为前向重访(forward revisit),这种优化的重访不会删除两个活跃事件之间添加的任何事件。
其余的探索以类似的方式进行。执行 ② 完成后,TruSt~0~ 重新访问 $\R(x)$ 并将其 rf 更改为 $\W(x, 1)$,然后再次添加 $\R(y)$ 和 $\W(y, 1)$,产生执行 ③,并通过另一次 $\fr$ 重新访问 $\R(y)$ 也执行 ④。
TruSt~0~ 能够以这种优化方式回溯的原因在于它检查一致性的方式。事实上,正是因为一致性不依赖于跟踪中不同事件的顺序,TruSt~0~ 能够将冲突的读取和写入保留在图中,并且仅通过更改读取的 $\rf$ 边来逆转竞争。相比之下,基于交错的 DPOR 始终必须从跟踪中删除两个冲突事件(以及跟踪中稍后事件的因果前驱事件),以便稍后可以按正确的顺序重新添加它们。
TruSt~0~: The Backward Revisit Problem
下图中 $\br$ 是 backward revisits 的缩写。有些较早的读取(如 $R(y)$)和较晚的写入(如 $W(y, 1)$)之间的事件需要删除。这一回溯过程是:
- 限制图表仅包含 $\R(y)$ 之前添加的事件,以及 $\W(y, 1)$ 的 $\porf$ 前缀,即 $\W(y, 1)$ 本身;
- 添加其他事件,完成执行。
我们刚刚看到了 TruSt~0~ 如何通过更新执行图而不删除任何中间事件来解决 $\fr$ 的竞争逆转问题。然而,这种方法不适用于向后重访(backward revisits),即较早的事件是读取而较晚的事件是写入的情况,因为在读取和写入之间添加到图中的事件可能取决于读取的值因此需要将其删除。为了确保始终添加写入及其因果($\porf$)前驱,类似于 $\S 2.3$ 中的最佳 DPOR,TruSt~0~ 将重访写入的 $\porf$ 前驱存储在读取的重访集中。
我们再次使用 $\mathsf{w+w+rr}$ 示例来说明 TruSt~0~ 对 $\br$ 的处理,但现在假设程序事件按从右到左的顺序添加(参见图 6)。可以看到,TruSt~0~ 逐一添加事件,直到最终到达执行 ①。当添加 $\W(y, 1)$ 时,TruSt~0~ 注意到可以重新访问 $\R(y)$ 来从中读取,因此将一个项目添加到 $\R(y)$ 的重新访问集中,其中包含 $\W(y, 1)$ 的因果前缀。类似地,当添加 $\W(x, 1)$ 时,TruSt~0~ 将因果前缀为 $\W(x, 1)$ 的项目添加到 $\R(x)$ 的重访集中。
完成完整执行后,TruSt~0~ 以深度优先的方式探索记录的重访。因此,它从 $\R(y)$ 的 $\br$ 开始,因此它限制图表仅包含 $\R(y)$ 之前添加的事件,以及 $\W(y, 1)$ 的 $\porf$ 前缀,即 $\W(y, 1)$ 本身。
然后它添加 $\W(x, 1)$ 事件完成执行 ② 。请注意,此时,$\R(x)$ 的重访集中不需要记录任何内容,因为它已经包含 $\W(x, 1)$。
接下来,算法继续 $\br$ $\R(x)$。受限图现在仅包含第一个事件 $\R(x)$ 和没有任何其他因果前身的 $\W(x, 1)$。然后它添加 $\R(y)$(只能读取 0),然后添加 $\W(y, 1)$,完成执行 ③ 并 $\br$ $\R(y)$ 导致执行 ④。
直观地,我们可以想象由从写入 w $\br$ 读取 r 引起的图,就像添加 r 时,如果 w 的前缀已经存在于图中,就会发生向前重新访问 r。换句话说,如果我们在添加 r 之前添加了触发 w 所需的事件,那么 r 也可以从 w 读取。作为一个具体的例子,当 $\W(x, 1)$ 在图 6 中的执行 ② 之后重新访问 $\R(x)$ 时,我们从 $\br$ 获得的图表有效地模拟了添加 $\R(x)$ 时 $\W(x, 1)$ 已经存在的场景。
虽然保存前缀避免了 TruSt~0~ 的睡眠集等构造,但仅靠它还不足以消除重新访问集的需要。要了解这一点,请考虑 $\W(x, 1)$ 在导致执行 ① 和 ② 的步骤中可以执行的 $\br$ 。在这两种情况下,$\W(x, 1)$ 都可以重新访问 $\R(x)$ 并得出相同的图。然而,执行两次相同的 $\br$ 显然会导致重复。重新访问集合对于防止此类重复是必要的。
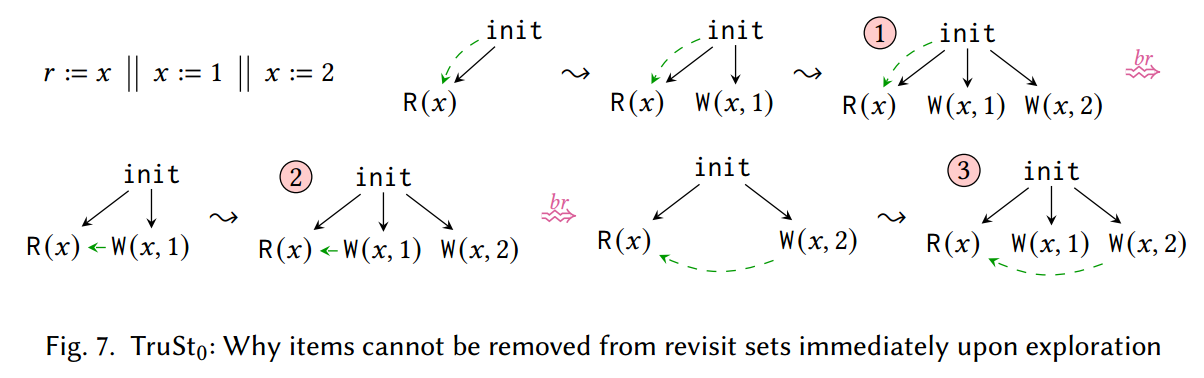
评论。事实上,在从图中删除相应的读取之前,重访集的任何项目都不能从集合中删除,如图 7 中的示例所示,为了简洁起见,我们不记录两次写入 x 之间的 $\co$。假设 TruSt~0~ 首先探索来自 $\W(x, 1)$ 的 $\br$,然后在执行 ① 后探索来自 $\W(x, 2)$ 的 $\br$ ,当在执行 ③ 中重新添加 $\W(x, 2)$ 时,我们必须记住它过去已经重访过 $\R(x)$。因此,一旦探索了这些项目,我们就无法从特定读事件的重访集中删除这些项目。
TruSt~1~: Achieving Optimality via Maximal Extensions
TruSt 通过确保特定的 $\br$ 只能在所有图中发生一次来避免重访集,在一种我们称为最大扩展(maximal extension)条件的新颖条件下,该条件要求必须以 $\co$-maximal 方式添加受重访影响(例如,删除)的所有事件。最大扩展条件允许我们完全消除重访集,并且可以被视为 TruSt 的基石:正如我们将在 $\S 3.5$ 中看到的,最大路径是 TruSt 实现多项式内存要求的原因。现在让我们将最大扩展条件合并到 TruSt~1~ 中。
最大扩展背后的关键思想很简单。考虑由于写事件 w $\br$ 事件 r 可能出现的(一致)图 $G'$。从前缀封闭性(参见 $\S 3.1$),我们还知道 $G'' \triangleq G' \setminus \set{r, w}$ 是一致的。从 $G''$ 开始并假设固定的构造顺序,如果我们添加程序的所有剩余事件,我们通常可以得到多个图 $G_1, G_2, \dots$ 具体取决于我们添加剩余事件的方式(例如、读取的 $\rf$ 边等)。原则上,这些都是可以导致从 w $\br$ r 的图。我们的目标是只允许在其中一个图 G 中进行此类重新访问,并确保这样的图存在。我们通过要求(1)以 $\co$-maximal 方式添加 G 中的所有附加事件(2)在构造 G 时不发生重新访问 来实现这一点。之所以具有唯一性,是因为只有一种选择 $\rf/\co$ 扩展,当没有重访发生时,它会使给定事件达到 $\co$-maximal,而存在性则来自于最大可扩展性(参见 $\S 3.1$):因为 $G''$ 是一致的,所以它以 $\co$-maximal 方式添加事件总是一致的。
现在让我们将这种直觉形式化。我们说写事件 $w \in G.W$ 对于一组事件 E 是的 $\co$-maximal 值,意味着 $w \in E$ 并且不存在 $w' \in E$ 使得 $\langle w, w' \rangle \in G.\co$(即,w 后面没有其他写事件)。读取事件 $r \in G.R$ 关于一个事件集合 E 是 $\co$-maximal 意味着 $G.\rf(r)$ 对于 E 是 $\co$-maximal。我们说事件 $e \in G.E$ 被最大添加(maximally added)在写入事件 $w \in G.W$ 之前,意味着 e 关于集合 $\Previous_G(e, w) \triangleq \set{e' \in G.E | e' \le_G e \vee \langle e', w\rangle \in G.\porf}$ 是 $\co$-maximal,且不存在 $r \in \Previous_G(e, w)$ 使得 $G.\rf(r) = e$。
定义 3.3(最大扩展)。执行图 G 是从 $w \in G.W$ 到 $r \in G.R$ 的潜在 $\br$ 的最大扩展,如果每个 $e \in G.E$ 使得 $r \le_G e$ 和 $\langle e, w \rangle \notin G.\porf$ 被最大添加在 w 之前。
上述定义与上面的直观描述密切相关,因此让我们在牢记上述解释的同时详细了解它。首先,请注意事件 e 的 $\co$-maximal 性是通过关于集合 $\Previous_G(e, w)$ 检查的,该集合包含 e 和在其之前添加的所有事件,以及(严格)在 w $\porf$-before 的事件,因为后面的事件将包含在结果图 G' 中。其次,请注意,只有 r 及其之后添加的所有事件才需要 $\co$-maximal 性,不包括那些严格位于 w 之前的事件(即,包括 w 本身)。排除 w 的严格 $\porf$ 前缀的原因是,如前所述,该前缀将包含在结果图 G' 中。另一方面,之所以包含 w 是因为,当从 G'' 开始时,我们通常可以通过多种不同的方式添加 w,只要它与 w 的位置有关。涉及到要删除的事件,因此我们必须选择一个。最后,请注意 $\Previous_G(e, w)$ 的定义禁止 $\br$ 已删除的事件。

现在让我们看一个示例,说明 TruSt~1~ 如何避免两次考虑相同的 $\br$ ,再次使用 $\mathsf{w+w+rr}$ 示例和图 6。如前所述,从 $\W(x, 1)$ $\br$ $\R(x)$ 在执行 ① 和 ② 中被检查两次。然而,根据定义 3.3,仅在执行 1 时考虑 $\br$ ,因为 $\R(y)$、$\W(y, 1)$ 和 $\W(x, 1)$ 都是以 $\co$-maximal 方式相加的。(请注意,$\R(y)$ 不是从 $\W(y, 1)$ 读取,这是执行 ① 中的 $\co$-maximal 写入,但这没关系,因为我们只希望事件在添加时达到最大。)相比之下,图 ② 不是相同重访的最大扩展,因为 $\R(y)$ 没有被最大程度地添加:它是从 $\W(y, 1)$ 读取的,它被添加到它之后的图中,并且不属于 $\W(x, 1)$ 的 $\porf$ 前缀。
理解为什么 TruSt~1~ 不应该在执行 2 中重新访问 $\R(x)$ 的另一种方式是,通过这样做,它将取消 $\W(y, 1)$ 之前对 $\R(y)$ 的重新访问。情况确实如此:最大扩展约束确保 $\br$ 不能包含在将被后续 $\br$ 删除的事件中。
正如我们很快就会看到的 ($\S 3.5$), TruSt~1~ 避免撤消已经完成的工作,以及重访集有效地转换为重访列表(因为 TruSt~1~ 不再需要保留前缀)这一事实,是对于在 TruSt 最终版本中实现多项式内存要求至关重要。
TruSt: From Exponential to Linear Memory Requirements
尽管最大路径渲染重访集已过时(从某种意义上说,TruSt~1~ 不需要记住已 $\br$ 每次读取的序列),TruSt~1~ 仍将可以重访每次读取的序列存储为重访列表的一部分。然而,正如 $\S 2.3$ 中的 exp-mem 所证明的,与回溯集类似,在我们开始从中删除项目之前,此类列表可能会变得指数级大,即使删除项目实际上是可能的。
现在让我们看看 TruSt 的最终版本如何扩展 TruSt~1~ 来解决上述问题。TruSt 的解决方案是热切地探索所有重访。也就是说,每当添加事件 a 时,TruSt 都会执行本地“竞争检测”阶段(即,如果 a 是读取,则查找 $\fr$,或者如果 a 是写入,则查找替代位置和 $\br$),并且,对于每个找到可能的替代方案后,它立即启动递归探索。例如,对于 $\mathsf{w+w+rr}$ 以及图 5 和图 6 中所示的探索,在这些探索中执行的每次重访都可以在每个重访事件恰好添加到图中的时间进行递归且热切地探索。
由于执行的 $\br$ 不会被后续 $\br$ 从图中删除,因此永远不会从图中删除的事件数量会增加。由于可以在图中添加的事件数量受到程序大小的限制,因此可以从给定图中执行的递归调用的数量也受到限制。一个简单的计算给我们提供了 $\mathcal{O}(n^3)$ 的空间复杂度界限,其中 n 是程序的大小:递归深度最多为 $n^2$(最多有 n 个 $\br$ ,其中任何对之间最多可能已添加 n 事件)并且每个递归调用都使用 $\mathcal{O}(n)$ 空间来存储执行图。
通过巧妙的数据结构和更仔细的计算,我们可以将 TruSt 的内存需求降低到 $\mathcal{O}(n)$。关键思想是存储单个执行图,并让所有递归调用在调用时更新图,并在返回时回滚更新。向前回滚很容易,因为它们仅更新一个 $\rf$ 或 $\co$ 边。此外,通过以固定顺序执行它们,人们不需要记住任何信息即可返回到先前的状态。回滚 $\br$ 有些困难,但仍然可以通过每次 $\br$ 仅保留恒定量的信息来实现。具体来说,由于读取可能会被来自唯一配置(图是最大扩展)的写入 $\br$,因此为了获得该配置,只需从图中删除重新访问的读写对并保持最大程度地添加事件,直到已达到重访写入。
现在让我们将所有内容放在一起,看看 TruSt 如何验证不同的程序,即下面的 $\mathsf{r+w+w}$ 程序:
$$ a := x \parallel x := 1 \parallel x := 2 $$
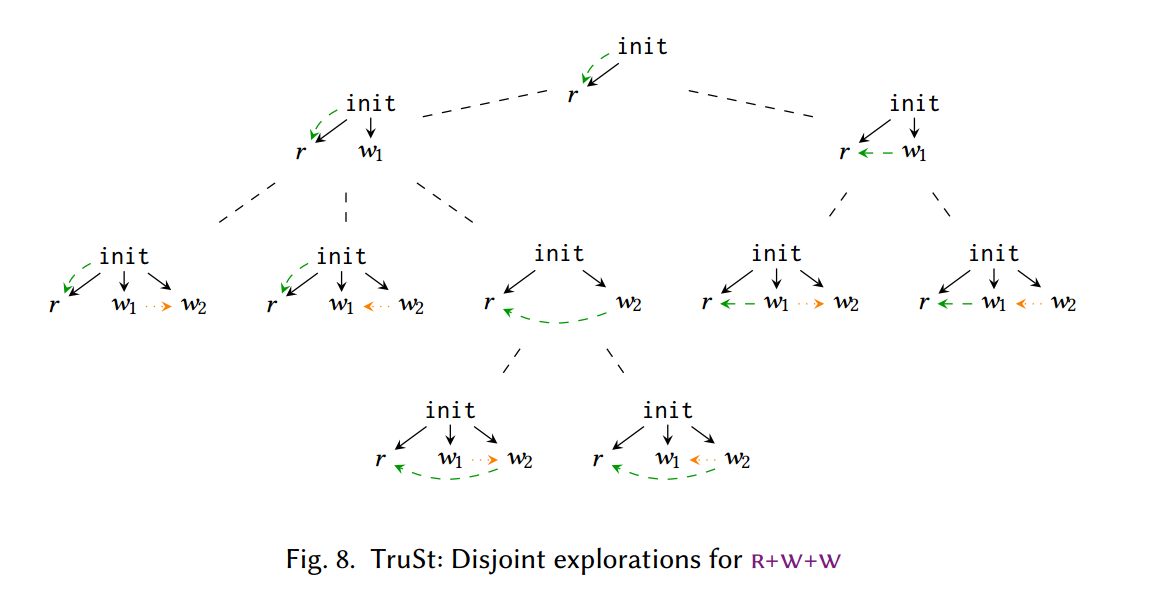
该程序在 SC 下有 6 个执行,可以在图 8 的探索过程的叶节点处看到(假设 TruSt 从左到右探索)。
由于 TruSt 急切地执行重访,因此当 TruSt 第一次遇到 $\W(x, 1)$ 时,它可以选择重访 $\R(x)$,也可以不重访;对于每种情况,TruSt 都会启动递归子探索。(请注意,重新访问 $\R(x)$ 是可能的,因为当前图是 $\W(x, 1)$ 重新访问 $\R(x)$ 时生成的图的最大扩展。)假设 TruSt 首先探索非重新访问的情况,接下来它将在所有可能的情况下添加 $\W(x, 2)$ 共同职位。如果 $\W(x, 2)$ 被最大程度地相加,TruSt 还可以选择重新访问 $\R(x)$,从而也递归地探索该选项。在这种情况下,$\W(x, 1)$ 被重新添加到图中,但现在它无法重新访问 $\R(x)$,因为后者没有被最大程度地添加(它已通过不在 $\W(x, 1)$ 的 $\porf$ 前缀中的写入 $\br$)。最后,TruSt 探索了第二个顶级递归调用,其中 $\W(x, 1)$ $\br$ $\R(x)$。当重新添加 $\W(x, 2)$ 时,它无法重新访问 $\R(x)$,因为它再次没有在 $\W(x, 2)$ 之前最大程度地添加。然而,TruSt 将探索 $\W(x, 2)$ 所有可能的一致性放置,从而完成对该程序的验证。
TruSt: Features and State-of-the-Art
我们通过关于 TruSt 和当前最先进技术的两个观察来结束本节。
首先,如 $\S1$ 中所述,TruSt 可以适应在 $\rf$ 等价下运行,该等价比 Mazurkiewicz 等价呈指数级粗糙。按照 Kokologiannakis 等人 [2019] 的说法,在这种 $\rf$ 分区下,TruSt 不会记录 $\co$,而是计算由于程序读取观察到的写入而产生的任何诱导的(induced) $\co$ 边。通过这种分区,TruSt 仅探索 $\mathsf{r+w+w}$ 的 3 次执行,因为 $\W(x, 1)$ 和 $\W(x, 2)$ 始终保持无序。
对于 $\mathsf{r+w+w}$ 程序:
$$ a := x \parallel x := 1 \parallel x := 2 $$
以下两个执行历史 $\rf$ 等价,尽管 $\W(x, 1)$ 和 $\R(x)$ 的相对顺序和关系不同:
$$ \init-\W(x, 1)-\W(x, 2)-\R(x, 2) \ \init-\W(x, 2)-\R(x, 2)-\W(x, 1) $$
因为这两个执行历史中每个 $\R$ 读到的值等价,即两个历史对应的树状历史等价,而树状历史(如图 6)不关心 $\co$ 边。
将 TruSt 扩展到 $\rf$ 等效性时的困难在于“相干性最大化”不再适用。正如 $\mathsf{r+w+w}$ 等示例所示,根据诱导的 $\co$ 边,可以有多个最大写入,这反过来又可以创建许多最大扩展。我们用一个平局制动(tie-braking)标准——来解决这个问题,从这些最大写入中选择一个:正如我们在 $\S 4.2$ 中所示,使用确定性平局制动标准(例如,$\le_G$ 关系),我们可以扩展 TruSt 来进行这样的分区对核心算法的改变最小。
其次,TruSt 的结构本质上是可并行的。尽管最佳 DPOR 算法已经并行化(例如,[Lång et al 2020]),但这种并行化涉及这些算法的实现,而不是算法本身,因为需要数据共享。TruSt 是第一个最佳的、与内存模型无关的 DPOR,它完全不需要在不同线程之间共享,因为如 $\S 3.5$ 所示,不同的重新访问可以以完全不相交的方式进行。
ALGORITHM
在本节中,我们将介绍模型检查算法 TruSt 的完整版本。首先,在 $\S 4.1$ 中,我们提出了 Mazurkiewicz/Shasha-Snir 等价的 TruSt 变体,它完全跟踪 $\co$,类似于 $\S 3$ 中的假设。然后,在 $\S 4.2$ 中,我们调整 TruSt 以实现更粗略的读取等价性,从而避免跟踪 $\co$。最后,在 $\S 4.3$ 和 $\S 4.4$ 中,我们分别概述了算法的合理性、完整性和最优性的证明,并分别限制了其内存消耗。
Algorithm Overview

TruSt 的算法可以在算法 1 中看到。给定一个输入程序 P,Verify 通过使用仅包含初始化事件的执行图 $G_\emptyset$ 调用 Visit 来验证 P。随后,Visit 将以深度优先的方式枚举 P 的所有执行图,并确保它们都不包含错误,即安全违规。
现在让我们仔细看看 Visit 函数,它是验证过程的核心。在每一步中,只要当前执行图 G 根据底层内存模型(第 4 行)保持一致,Visit 就会通过调用 nextP (G) 来扩展当前图 G。
函数 nextP (G) 找到一个既没有阻塞也没有完成的线程,将相应的事件添加到 G.E 和 $\le_G$(使其最大化),并通过 a 返回它(第 5 行)。它不会更新 $G.\rf$ 和 $G.\co$。从技术上讲,我们假设事件上存在某种总顺序 $<_{\next}$,表明 $\next_P()$ 对于首先添加哪个事件的偏好。我们假设 <next 遵循程序顺序(即 po ⊆ <next),并且对应于相同读取-修改-写入 (RMW) 指令的任何读取和写入事件在 <next 中都是相邻的。给定一组可以添加到 G 的可用事件的 avail(G)(即,程序的每个未终止、非阻塞线程的下一个事件的集合),nextP (G) 将最小的此类事件添加到 G w.r.t. <下一个。特别是,这意味着如果 G 包含与成功 RMW 指令的读独占事件相对应的事件,而没有其匹配的写独占事件,则 nextP (G) 将返回该写独占事件(无论如何,它紧随其后) )。如果没有可用事件,我们说执行图 G 已满,并且 nextP (G) 返回 ⊥。
Visit 采取的下一步行动取决于 a 本身。
- 如果 a 为 ⊥ 或错误,则 Visit 分别返回(第 6 行)或引发错误(第 8 行)。
- 如果 a 是读取,Visit 需要计算新添加事件的所有可能的 rf 选项。为此,对于每次将 w 写入与 a 相同的位置(第 11 行),如果 G rf(r) 映射到 w,它会在结果图上递归调用 Visit。任何不一致的选择随后将通过相应递归调用第 4 行的一致性检查来消除。
- 如果 a 是写入,如 $\S3$ 中所述,则访问需要检查 a 不重新访问任何图形读取的情况以及 a 重新访问 G 中的某些读取的情况。
为了处理第一个案例,Visit 致电 VisitCO(第 14 行)。对于 G 中 a 的每个可能的共同前任 w𝑝,VisitCOs 将通过 SetCO(G w𝑝 a) 在 co 中的 w𝑝 之后立即插入 a,然后在结果图上调用 Visit(第 22 行)。形式上,$SetCO(G, w_p, w)$ 返回一个新图 G' ,它与 G 相同,只是它的 $G'.\co$ 分量设置为:
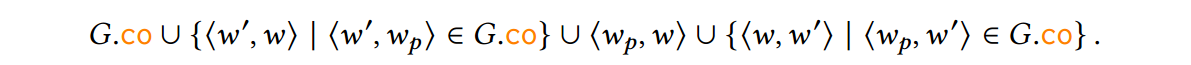
处理 a $\br$ G 中的某些内容的情况自然更具挑战性,因为它反映了 TruSt 的本质及其最大扩展条件。 Visit 迭代所有作为 a 的相同位置读取,这些读取不是 a 之前的 $\porf$-before a 作为 $\br$ 的候选者(第 15 行)。 ($\porf$-before a 之前的读取被排除,因为重新访问它们会创建 $\porf$ 循环,这是图良构所禁止的;参见 $\S 3.1$。)对于每个候选读取 r,Visit 计算将被删除的事件集如果 a $\br$ r(第 16 行),则从 G 开始,并通过调用 IsMaximallyAdded(第 17 行)检查是否已最大程度地添加了 r 和要删除的所有其他事件 e。如果是这样,Visit 通过删除已删除的事件来适当限制 G,使 r 从 a 读取,然后调用 VisitCO 来探索新图中 a 的所有可能的一致性位置(第 18 行),从而实现 $\S3$ 中描述的 $\br$ 过程。
因此,IsMaximallyAdded(G e w) 紧密遵循事件 e 在 G 中的 w 之前最大添加的定义(参见 $\S 3.4$)。首先,它计算先前事件的集合 Previous(即,在 e 之前添加的事件或在 a 之前 G $\porf$-before 的事件)。接下来,它检查是否有其他事件 r 已被 e 向后访问,如果是,则返回 false。然后,如果 e 是一个写入事件,它会检查 e 本身在 Previous 中是否是 $\co$-maximal 值。如果 e 是读取事件,它会检查 e 是否从 Previous 中的 $\co$-maximal 事件读取。请注意,如果 e 既不是读取也不是写入(例如,栅栏事件),则极大性检查通常会成功。
最后,回到 Visit 的 switch 语句,对于所有其他事件情况(例如,内存栅栏),Visit 只是启动一个递归调用(第 19 行),无需特别注意。
至此,我们对 TruSt 的介绍就完成了。然而,关于算法 1,有两点值得一提。
第一个是,当 $\br$ 时,Visit 在创建新图后设置 a 的相干放置。反过来,人们可能会想:为什么不在图形被限制之前设置它,以便所述放置可以用于重访和非重访情况?这个问题的答案是,如果 Visit 这样做了,那么它还必须对 a w.r.t. 的共同排序进行额外检查。已删除的事件。
值得一提的第二点是,算法 1 可以多次 $\br$给定的读取,尽管 $\br$通常会被保留。这样做常常是获得某些结果所必需的。图 9 中显示了一个这样的示例。对于 r+ww 示例,只有重新访问 $\R(x)$ 两次才能获得 a := x 读取注释值的执行:在子探索中 $\R(x)$ 没有最大程度地添加到 $\W(x, 2)$ 之前其中它没有被 $\W(x, 1)$ 重新访问并保持读数 0,从而排除了 $\W(x, 2)$ 重新访问 $\R(x)$。更一般地说,尽管最大扩展禁止从已删除事件 $\br$,但它们确实允许从 $\porf$ 相关存储 $\br$。
TruSt: Adaptation for a Reads-From Equivalence Partitioning
虽然算法 1 枚举了给定程序的所有一致执行图,但它同时还跟踪相同位置写入之间的完全一致性 (co)。事实上,正如第 3.4 节和第 4.1 节中所解释的,在检查最大扩展时, $\co$-maximal 性的概念对于 TruSt 来说至关重要。
然而,许多最近的 DPOR 方法避免跟踪完全的一致性(例如,[Abdulla et al 2019; 2018; Chalupa et al 2017; Kokologiannakis et al 2019; 2020])。如果不这样做,他们会获得指数级粗略的等价分区,通常称为读取等价分区。虽然尚不清楚这种分区是否会对现实工作负载的验证时间产生实际影响 [Kokologiannakis et al 2019],但它可能会导致在具有无序、并发、同一位置写入的程序中探索指数级减少的执行次数。
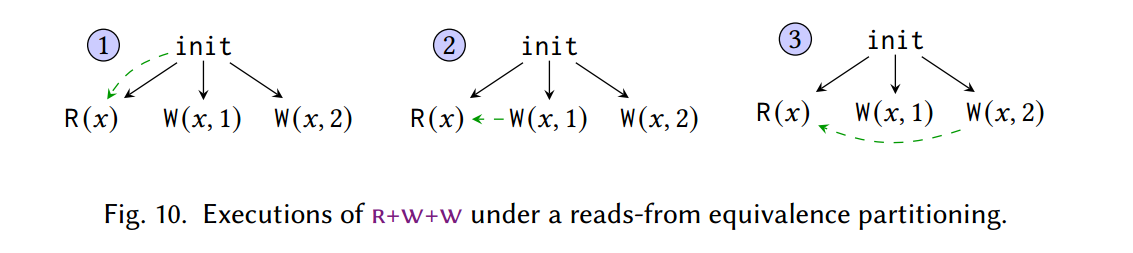
作为一个例子,再次考虑 $\S 3.5$ 中的 $\mathsf{r+w+w}$ 程序及其在读取等价分区下的执行,如图 10 所示。在这种分区下,对 x 的两次写入保持无序,因为任何程序的读取都不会遵守它们的顺序。在程序验证方面,在这种划分下运行的模型检查器可以通过仅枚举 3 次执行(而不是 6 次)来验证 $\mathsf{r+w+w}$ 程序。
一般来说,DPOR 避免对未观察到的并发写入进行排序的方法是用仅部分对相同位置写入进行部分排序的不同一致性关系替换 co。对于 GenMC(以及扩展后的 TruSt),这种关系称为 writes-before (wb) [Kokologiannakis et al 2019;拉哈夫等人 2015]。为了了解 wb 的工作原理,请考虑图 11 中的示例。在所描绘的执行图中,第一个线程的两次写入按 wb 排序,因为 $\W(x, 2)$ 是 po-在 $\W(x, 3)$ 之前。此外,$\W(x, 1)$ 必须在 $\W(x, 3)$ 之前为 wb-,否则 $\R(x)$ 将因一致性而读取 1。但是,请注意 $\W(x, 2)$ 和 $\W(x, 1)$ 保持无序:只要 wb 遵守 x,这两个写入就可以按任一顺序执行,并且无法观察到此顺序。
此时,必须提出一个问题:我们能否将 TruSt 的最大扩展思想(严重依赖 co)与 wb 之类的关系(通常避免排序并发写入)结合起来?
幸运的是,答案是肯定的,但实现起来却很棘手。显然,在最大添加事件的定义中,不能简单地将 co 替换为 wb,因为在一致的执行图中可能存在多个 wb 最大写入。为了保持最优性,我们需要在这些 wb-maximal 事件之间建立一个平局。一个简单的解决方案是选择一个任意的仲裁者(例如,最后插入到图表中的写入,即 wb-maximal 事件中的 <G -maximal 事件)。该解决方案有效,但它需要底层内存模型具有更强的可扩展性:使用从任何 wb-maximal 事件读取的读取事件扩展一致的执行图应该会产生一致的图。虽然此属性适用于某些简单模型,例如释放-获取一致性,但它不适用于其他模型,包括 SC。问题在于,虽然一致图的 co 必须是扩展 wb 的某个位置总阶,但并非所有扩展 wb 的位置总阶都满足模型的一致性谓词。

在算法 2 中,我们提出了一个更好的解决方案,它仅假设有一种由函数 GetConsCO 给出的方法来计算图一致的相关关系。该函数的简单实现是以系统方式枚举扩展 wb 的所有位置总订单,并返回满足模型一致性谓词的第一个订单。更好的实现可以通过更有效的方法来检查不包含协同组件的执行图的一致性(例如,[Abdulla et al 2019; Biswas et al 2019; Bui et al 2021])。
我们的改编算法(以下称为 TruSt/wb)通过在图的部分上调用函数 GetConsCO 来获得合适的相关性,该部分将在 $\br$ 时保持不变,并将任何将被重访删除的写入附加到该顺序的末尾按照他们的插入顺序。因此,通过构造,所有删除的写入都将满足最大值条件。如果删除的读取是从插入到它们之前的图中的最后一个删除的相同位置写入(如果存在这样的写入)读取的,或者从根据 GetConsCO 返回的订单。
唯一需要的其他更改是 VisitCO 的定义:由于 TruSt/wb 不跟踪完全一致性,VisitCO 简单地归结为 Visit 调用,从而展示了 TruSt/wb 潜在提供的指数级改进。
TruSt: Soundness, Completeness & Optimality
假设输入程序 P 的执行次数只有有限大小,我们表明 TruSt 算法(算法 1)总是终止,并且是健全的、完整的和最优的。健全性确保如果 Verify(P) 生成 G,那么 G 是一致的完整程序执行。完整性确保如果 G 是 P 的一致完整执行,则 Verify(P) 将生成 G。最优性确保 TruSt 准确地生成每个执行一次,并且从不进行浪费的探索。 Kokologiannakis 等人 [2022] 中完整给出了这些结果的证明;我们继续进行概述。
算法终止。我们首先表明,一旦任何 writew $\br$某些 readr,它就无法在任何后续子探索中删除。通过矛盾,假设通过写入 w ' $\br$某些先前的读取 r ' 来删除 w 。如果 r ' ≤ r,则 r 必须位于已删除事件集中,以便重新访问 r ' ,否则 w 不会被删除。但在这种情况下,r 本身无法被删除,因为它在 w ' 之前尚未被最大程度地添加:它从在其之后添加的已删除事件 w 中读取。否则,它必须是 r ' > r,但在这种情况下,w 无法被删除,因为未删除的事件 (r) 正在从中读取。
算法 1 的终止源自以下假设:P 的所有执行都是有界大小的。由于除了 $\br$ 之外的所有算法步骤都会增加图的大小,并且由于无法删除发起 $\br$ 的写入,因此只能有有限数量的 $\br$ ,因此只能有有限数量的算法步骤。
健全性。 TruSt 非常合理,因为事件按照程序语义添加到图中,而不一致的执行一旦到达就会被删除。
完整性。完整性表明,Verify(P) 访问 P 的每个一致的完整图。
定理 4.1(完备性)。令 G𝑓 成为 P 的一致完整执行图。然后,Verify(P) 为某个图 G' 𝑓 ≈ G𝑓 调用 Visit(P G' 𝑓 )。
证明背后的关键思想是,给定算法达到的执行 G,我们可以推断出在导致 G 的(唯一)生产序列中紧邻它之前的执行。这一观察使我们能够定义一个过程 Prev(算法 3),将每个非空一致执行映射到其“上一个”执行。 Prev 让我们退后一步;从 G 到唯一执行 G𝑝,这样 Visit(P G𝑝 ) 立即导致 Visit(P G) 调用。
我们表明,从 G𝑓 重复执行上一步最终将得到初始图:在每个点 G𝑓 的最大事件被删除或从较早的事件中读取。接下来,我们表明,只要图 G 通过一致的完整执行是 Prev 可到达的,并且 G𝑝 是可到达的算法配置,使得 Prev(G) = ⟨G' 𝑝 _⟩ 且 G' 𝑝 ≈ G𝑝 ,则 Visit(P G𝑝 ) 调用 Visit(P G' ) 对于一些 G' ≈ G。然后,定理 4.1 对来自 G𝑓 的 Prev-step 序列进行归纳。
最优性。最优性包括显示两个属性:(1)不存在重复的探索,(2)不存在注定会被阻止且永远无法完全执行的无结果的探索。
为了建立前者,我们首先证明对于每个可到达的算法配置 G,如果 G 执行算法步骤 𝑡 并达到配置 G',则 Prev(G') = ⟨G𝑡⟩。这是因为 𝑡 要么将最大事件添加到 G(非重访情况),要么将其读取的写入( $\br$ 情况)。无论哪种情况,Prev(G' ) 都会识别该步骤并取消它。
然后我们可以轻松证明不存在重复探索,因为每个配置 G 最多达到一次。 (通过矛盾假设有两个生产序列达到相同的配置。但是,我们刚刚证明它们必须具有完全相同的最后一步,现在我们有两个较短的生产序列达到相同的配置,通过归纳,它们也应该一致)
定理 4.2(无重复探索)。给定图 G,Verify(P) 在针对某些 G' ≈ G 调用 Visit(P G' ) 之前最多会经历一系列嵌套的 Visit(P _) 调用。
为了建立后一个属性,我们需要对涉及 RMW 事件处理的记忆模型进行额外的假设。我们说内存模型是独占写入可扩展的,如果对于所有具有 po 最大独占读 r ε G R ex 的一致图 G ,使得不存在具有立即 po- 的独占读 r ' ε G R ex 。后继(匹配)独占写入和 G rf(r ' ) = G rf(r),添加其相应的独占写入事件 w 产生一致的图(对于 co 的某些选择)。
然后,我们可以证明,如果可达算法配置无效,那么它会立即被阻止。事实上,可能出现无效配置的唯一方法是添加从另一个 RMW 已读取的写入中读取的 RMW 事件的读独占部分。下一步将添加其写入独占部分,从而使图形不一致。

TruSt: Iterative Version with Linear Memory Consumption
最后,我们提出了具有线性内存消耗的 TruSt 算法的迭代版本。为简单起见,在算法 4 中,我们展示了不记录 co 且适用于 rfe 等价的版本。该算法显然具有线性空间复杂度,因为它仅保留执行图 G 的一份副本以及用于跟踪 $\br$ 的辅助数组 B,并且不会递归地调用自身。
算法 4 以迭代方式运行,采用以下两种模式之一:(1) 前向模式,在可能的情况下不断向图中添加事件; (2) 回溯模式,当替代探索选项可能时,该模式改变图的 rf 边缘,删除事件(例如,执行 $\br$ 或当事件的所有重访选项都已被探索时),和/或恢复以下事件:已被需要撤消的 $\br$ 删除。
前向模式对应于算法 4 的外部 while 循环,非常简单。只要图形一致,图形就会随着下一个可用事件 a 进行扩展(第 3 行)。如果该事件表示错误,则验证失败并显示错误消息(第 4 行)。如果 a 是读,则其 rf 根据插入顺序设置为同一位置的最大写。如果 a 是写入,我们初始化它在 B 数组中的索引。否则,如果执行完成(或不一致),我们将进入回溯模式(第 8 行)。
回溯模式对应于内部 while 循环,并且更微妙一些。首先从 G 中选择最大事件 a(第 9 行)。如果不存在此类事件(即图中仅包含初始化事件),则回溯完成,验证完成(第 10 行)。现在,如果 a 存在并且是一个读取事件,我们必须检查 a 是否还有任何未考虑的剩余 $\fr$ 选项。如果还有更多可能的写入可供 a 读取,按插入顺序早于写入 a 当前正在读取的写入(第 11 行),那么我们将 a 设置为从最大此类写入中读取(第 12 行),然后返回到前向模式(第 13 行)。
类似地,如果 a 是一个写入事件,我们必须检查是否有任何(进一步的)读取需要由 a $\br$。如果有这样的读取(第 14 行),我们根据插入顺序选择最新的,并将其存储在 B[a\(第 15 行)中。然后,如果所选读取满足最大扩展条件(第 18 行),我们将其 rf 更新为从 a 读取(第 19 行),限制图(第 20 行),然后返回正向模式(第 21 行)。
最后,如果 a 没有任何剩余的重访选项,我们调用 Prev(G)(算法 3),返回上一个执行步骤(第 22 行)。如果这不是 $\br$ 步骤,我们只需从 G 中删除最大事件(第 23 行)。然而,如果这是从图 G𝑝 (第 25 行) $\br$,我们需要做更多的工作来重建 G𝑝 中的正确事件序列。
为此,对于 a 之前的事件,我们遵循 G 中的事件顺序,对于已删除的事件,则遵循插入顺序。每当删除的事件 𝑑 从稍后(按插入顺序)的 G 事件读取时,这意味着 𝑑 已被 $\br$;因此,我们还在 𝑑 之后立即添加 G 的所有先前(尚未添加)事件:操作 ra XX rb 返回 ra ∪ rb ∪ dom(ra) × dom(rb)。
IMPLEMENTATION
在第 1 节和第 3 节中,我们强调内存模型参数化是 TruSt 的关键特征之一。为了在内存模型的选择上实现参数化,我们在 GenMC 之上实现了 TruSt [Kokologiannakis et al 2019]。 GenMC 的实现是开源的 (https://github.com/mpi-sws/genmc),并且内置了对 RC11 等弱内存模型的支持 [Lahav et al 2017]。
也就是说,尽管 GenMC 的架构通常是模块化的并且允许扩展,但我们必须大幅修改 GenMC 的现有实现,以集成 TruSt 所需的更改并适应 TruSt 的并行化。后一部分可以说是技术方面最具挑战性的部分。
就 TruSt 的顺序实现而言,我们的实现主要遵循 TruSt 算法的递归版本,但在原地执行 $\fr$ ,并且仅复制图以进行 $\br$ 。虽然这意味着我们的实现会消耗二次空间,但我们相信它比 TruSt 的纯迭代版本更快,后者需要在每次 $\br$后通过重新解释程序来重建执行图。此外,正如我们的实验所证实的那样($\S 6.1$),我们实现的内存消耗从来都不是问题。
就 TruSt 的并行实施而言,我们面临两大挑战。第一个挑战是 GenMC 使用多个非线程安全的 LLVM 内在函数。因此,为了排除由于 GenMC 所依赖的内部 LLVM 库导致的并发错误,我们重新设计了 GenMC 基础设施的很大一部分,以减少其对 LLVM 内在函数的依赖,以便不同的线程可以以线程安全的方式进行通信。
我们必须处理的另一个问题是不同线程之间通信的设计。为此,我们选择了以下简单的解决方案:由于 TruSt 每当启动递归 $\br$ 探索时都会复制当前执行图,因此在多核设置中,它可以简单地将图副本传递给另一个工作线程,以便两个探索可以并行进行。诚然,这样的设计依赖于给定程序中有足够的 $\br$ ,但我们仍然发现它在实践中提供了良好的可扩展性。尽管我们还尝试为每个线程提供自己的工作窃取队列,但我们发现这种方法与我们当前的实现相比并没有带来任何好处。
将所有内容放在一起,我们获得了 TruSt 的实现,它具有多项式内存要求,并充分利用底层机器的并行性 ($\S 6.2$)。正如我们在 $\S 6.1$ 中所示,TruSt 的性能与最先进的 DPOR 实现相当。
EVALUATION
我们的评估围绕验证 $\S1$ 的主张展开。具体来说,我们着手展示以下两点:(1) TruSt 提供了两全其美的优点:最优性和多项式内存消耗。
(2) TruSt 本质上是可并行的:它可以扩展到大量核心,因为不同的探索不共享状态。
为了证明第一点($\S 6.1$),我们进行了包括两部分的评估。在第一部分中,我们将 TruSt 与其他两个无状态模型检查器进行了比较,即 GenMC 和 Nidhugg [Abdulla et al 2015; 2014]。我们选择 GenMC 是因为 TruSt 是建立在它之上的(也因为它的 DPOR 算法是最优的),而 Nidhugg 是因为它提供了最优和非最优(基于睡眠集)DPOR 算法,从而很好地突出了时间和内存之间的权衡 DPOR 算法必须付出代价。在第二部分中,我们在一组现实的弱内存基准测试上针对 GenMC 评估了 TruSt。由于 Nidhugg 不支持类似于 GenMC RC114 的内存模型,并且内存消耗直接取决于模型允许的执行次数,因此我们必须将其排除在本次比较之外。正如我们在 $\S 6.1$ 中所示,TruSt 总是比非最佳 DPOR 实现指数级快,并且比最佳 DPOR 实现指数级“轻”(就内存消耗而言)。尽管 TruSt 可能比最佳 DPOR 慢多项式,但我们观察到 TruSt 面临的开销微不足道。相比之下,在最佳 DPOR 消耗指数量内存的情况下,TruSt 的速度可以指数级加快,因为它的计算不会受到内存限制。为了保持比较公平,在这两个部分中,我们仅使用一个工作线程运行 TruSt,因为其他工具不支持相同程度的并行性。
为了演示第二点 ($\S 6.2$),我们在多个较大的基准测试中使用越来越多的线程来评估 TruSt 的并行实现。正如我们在 $\S 6.2$ 中所示,当扩展到可用物理核心数量时,我们的原型实现实现了几乎线性的加速,从而产生了显着的性能改进。
实验装置。我们在 Dell PowerEdge M620 刀片系统上进行了所有实验,该系统运行基于 Debian 的自定义发行版,配备两个 Intel Xeon E5-2667 v2 CPU(8 核 @ 3.3 GHz)和 256GB RAM。我们对 Nidhugg、GenMC 和 TruSt 使用 LLVM 7.0.1。除非另有明确说明,所有报告的时间均以秒为单位。我们设置了 24 小时的超时限制和 500MB 的内存限制。
TODO
RELATED WORK
在 Verisoft 等开创性作品之后 [Godefroid 1997; 2005] 和 Chess [Musuvathi et al 2008] 为无状态模型检查铺平了道路,关于 SMC 和 DPOR [Flanagan et al 2005] 已经有大量工作。 Abdulla 等人 [2014] 在这方面取得了重大突破,他们为 Mazurkiewicz 迹等价提供了第一个最优 DPOR 算法,以实现顺序一致性。如 $\S 2.3$ 中所述,该算法避免了以指数内存消耗为代价的阻塞探索。我们可以根据其主要关注点将这一领域的最新作品大致分为两大类。
首先,许多技术旨在通过引入更粗糙的等价划分来解决状态空间爆炸问题[Abdulla et al 2019;阿加瓦尔等人 2021;艾伯特等人 2017; 2018;阿罗尼斯等人,2018;查卢帕等人 2017; Chatterjee 等人 2019]。其中,只有 Nidhugg [Abdulla et al 2019; Aronis et al 2018] 是最优的。尽管如 6.1 中所示,其等价分区可能会遭受指数内存消耗的影响。
其次,其他技术侧重于通过针对特定的弱内存模型将 DPOR 扩展到弱内存模型 [Abdulla et al 2015; 2016 年; 2018; Norris et al 2013] 或通过相对于公理定义的内存模型进行参数化 [Kokologiannakis et al 2019; 2020]。此外,其中许多工作可以在更粗略的读取等价分区下运行,包括 Abdulla 等人 [2018] 和 Kokologiannakis 等人 [2019, 2020],它们在保持最优性的同时做到了这一点。 TruSt 建立在 GenMC [Kokologiannakis et al 2019] 奠定的基础上,以实现内存模型参数化;但是,它将底层内存模型的“可扩展性”要求调整为更精确的“最大可扩展性”要求(参见 $\S 3.1$)
然而,与 TruSt 相比,上述技术都没有能够将 (a) 参数化与 w.r.t 结合起来。内存模型,(b) 在读取等效性下运行,(c) 最优,以及 (d) 保持多项式内存消耗。在某种程度上,Nguyen 等人 [2018] 已经利用准最优 DPOR 探索了 (c) 和 (d) 之间的组合。准最优 DPOR 能够使用用户提供的常数 𝑘 来近似最优 DPOR。随着 𝑘 值的增加,内存消耗也呈指数增长。尽管准最优 DPOR 理论上仅在 𝑘 = ∞ 时才达到最优,但事实证明,对于较小的 𝑘 值,它实际上是最优的。
最后,值得思考的是,是否可以使用最大扩展的思想来实现像 RCMC [Kokologiannakis et al 2017] 这样的算法的最优性,该算法并不是严格意义上的 DPOR 算法。不幸的是,事实证明最大扩展是不够的。要看到这一点,请考虑下面的程序:
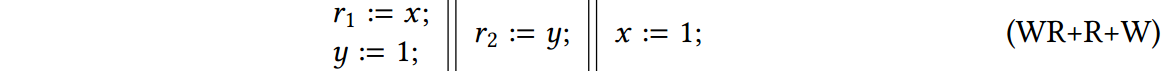
与 TruSt 不同,在 $\br$ 时,RCMC 仅删除重访事件的 $\porf$ 后缀,保持图表的其余部分完整。因此,当在 RCMC 中集成最大扩展时,RCMC 能够在 r2 = 0 和 r2 = 1 时重新访问 x 的读取,从而导致 r1 = 1 ∧ r2 = 0 两次执行。通过附加约束,很可能获得最优性;我们将其留给未来的工作。
结论和未来的工作
我们提出了 TruSt,一种优化的内存模型参数无状态模型检查算法,可协调 SMC 与 DPOR。 TruSt 提供了第一个保持多项式内存消耗的最佳 DPOR 框架。与之前的工作相比,TruSt 仅在要从当前执行图中删除的事件形成最大扩展(即它们以共最大方式添加)时才逆转两次内存访问之间的竞争。
未来,我们计划追求几个不同的研究方向。首先,我们计划放宽 TruSt 的波尔夫无环性假设,以便它也可以解释 POWER [Alglave et al 2014] 和 ARMv8/RISC-V [Pulte et al 2018] 等硬件内存模型。其次,我们计划通过设计更精细的消息传递方案来微调和优化 TruSt 的并行实现,该方案将允许在更大的基准测试中实现更大的可扩展性。最后,我们计划利用 TruSt 的低内存要求,并用它来验证大型软件系统的关键组件(例如 Linux 内核的数据结构)。

