$$ \def\SER{\mathsf{SER}} \def\PSI{\mathsf{PSI}} \def\SI{\mathsf{SI}} \def\PC{\mathsf{PC}} \def\CC{\mathsf{CC}} \def\RA{\mathsf{RA}} \def\read{\mathtt{read}} \def\write{\mathtt{write}} \def\Event{\mathsf{Event}} \def\Obj{\mathsf{Obj}} \def\hist{\mathsf{hist}} \def\level{\mathsf{level}} \def\before{\mathsf{before}} \def\po{\mathsf{\textcolor{red}{po}}} \def\wr{\mathsf{\textcolor{teal}{wr}}} \def\ww{\mathsf{\textcolor{red}{ww}}} \def\rw{\mathsf{\textcolor{blue}{rw}}} \def\co{\mathsf{\textcolor{orange}{co}}} \def\CO{\mathsf{\textcolor{brown}{CO}}} \def\Int{\mathtt{Int}} \def\Ext{\mathtt{Ext}} \def\Prefix{\mathtt{Prefix}} \def\Conflict{\mathtt{Conflict}} \def\SerTotal{\mathtt{SerTotal}} \def\lthb{\lt_\mathsf{hb}} \def\ltar{\lt_\mathsf{ar}} \def\ltpo{\lt_\mathsf{po}} \def\DDG{\mathsf{DDG}} \def\SDG{\mathsf{SDG}} \def\I{\mathcal{I}} $$
摘要
为了实现可扩展性，现代互联网服务通常依赖于分布式数据库，其事务一致性模型比可序列化性要弱。目前，应用程序员通常缺乏确保这些一致性模型的弱点不会违反应用程序正确性的技术。我们提出了一些标准来检查依赖于仅提供弱一致性的数据库的应用程序是否具有鲁棒性，即其行为是否像使用提供可序列化的数据库一样。在这种情况下，应用程序员可以获得弱一致性的可扩展性优势，同时能够轻松检查所需的正确性属性。我们的结果系统而统一地处理了最近提出的几种弱一致性模型，以及一种增强应用程序各部分一致性的机制。
本文的研究对象的是分布式数据库及其一致性。
作者：
- Giovanni Bernardi, IMDEA Software Institute
- Alexey Gotsman, IMDEA Software Institute
Introduction
为了实现可扩展性和可用性，现代互联网服务通常依赖于大型数据库，这些数据库在大量节点和/或广阔的地理跨度上复制和分区数据（例如，[14、20、26、3、6、4、5、11、22、27、10]）。数据库客户端在任何节点上调用数据事务，节点之间使用消息传递相互传达更改。理想情况下，我们希望这个分布式系统能够提供关于事务处理的强保证，例如可序列化性 [8]：如果这些事务按某种顺序串行执行，则可以获得并发执行一组事务的结果。可序列化性很有用，因为它允许应用程序程序员轻松建立所需的正确性属性。例如，要检查应用程序的事务是否保留给定的数据完整性约束，程序员只需检查每个事务在单独执行时是否都保留了约束，而不必担心并发性。不幸的是，实现可串行化需要数据库节点之间进行过多的同步，这会减慢数据库的速度，甚至在副本之间的网络连接失败时导致数据库不可用 [17, 1]。因此，如今的大型数据库通常提供弱一致性保证，这允许非串行化行为，称为异常。
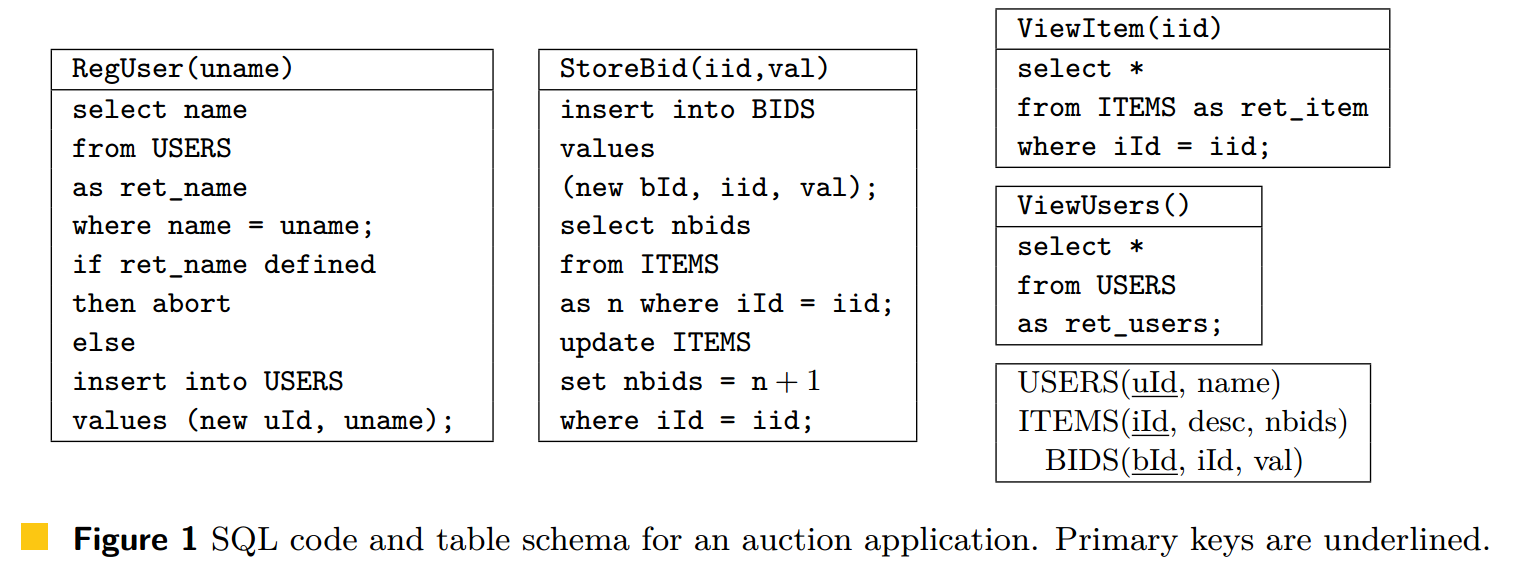
作为一个激励性的例子，考虑一个玩具在线拍卖应用程序，其交易由图 1 中的交易程序定义。程序 RegUser 创建一个新用户帐户。它操作表 USERS，该表的行包含主键 (uId) 和昵称。只有昵称 uname 未出现在 USERS 中时，RegUser(uname) 的调用才会在 USERS 中插入新行，以确保昵称是唯一的。程序 ViewUsers 可用于查看所有用户。某些数据库 [22, 26, 3] 可能允许执行 RegUser 和 ViewUsers，例如图 2(c) 中所示的那个。RegUser 的两次调用生成事务 T1 和 T2；它们写入两行 USERS，用 x 和 y 表示，以注册用户 Alice 和 Bob。然后程序 ViewUsers() 被调用两次；T3 中的调用看到 Alice 但没有 Bob，而 T4 中的调用看到 Bob 但没有 Alice。这个结果称为长分叉异常，无法通过以任何顺序执行这四个事务来获得，因此是不可序列化的。
过去几年，针对现代大型数据库提出了许多新的事务一致性模型 [22、11、26、3、5]，这些模型的不同之处在于它们通过暴露此类异常来削弱一致性，以换取更好的性能。不幸的是，应用程序程序员通常缺乏确保这些一致性模型的弱点不会违反应用程序正确性的技术。这种情况阻碍了主流数据库开发人员和应用程序程序员采用新的一致性模型。
解决此问题的一种方法是使用应用程序鲁棒性的概念 [16, 15, 9]。如果应用程序在使用该模型或序列化能力的数据库时表现相同，则该应用程序对特定弱一致性模型具有鲁棒性。如果应用程序对给定的弱一致性模型具有鲁棒性，那么程序员就可以获得使用弱一致性的性能优势，同时能够轻松检查所需的正确性属性。
在本文中，我们制定了针对三种最近提出的一致性模型检查应用程序鲁棒性的标准——因果（又名因果+）一致性（CC）[22]、前缀一致性[11]（PC）和并行快照隔离[26]（PSI，又名非单调快照隔离[3]）。作为我们研究结果的推论，我们还推导出了经典快照隔离模型[6]（SI）的现有鲁棒性标准[16]。我们的标准还处理一致性模型的变体，这些变体允许应用程序员要求在可序列化性下执行某些事务，从而确保原本不稳健的应用程序的鲁棒性。
我们利用最近提出的框架 [12] 以声明方式指定其语义（第 2 节），以统一和系统的方式处理上述四种一致性模型。特别是，我们考虑的所有一致性模型都保证事务的原子可见性：事务执行的所有写入操作要么可以被其他事务观察到，要么都不能被观察到。这使我们能够通过从应用程序执行中的事务内部抽象出来，来简化建立鲁棒性标准所需的推理。我们首先提出一个动态鲁棒性标准，用于检查给定执行是否可序列化（第 3 节）。我们根据执行的依赖关系图 [2] 制定此标准，描述其事务之间的几种关系：如果执行的依赖关系图不包含某种形式的循环，则执行是可序列化的，我们称之为关键（critical）。针对不同一致性模型的鲁棒性标准在哪些循环被视为关键方面有所不同。然后，我们说明如何将单个执行上的动态鲁棒性标准提升为静态标准，以检查给定应用程序的所有执行是否可序列化（第 4 节）。
Consistency Model Specifications
我们首先回顾一下 [12] 中数据库计算的正式模型和我们处理的一致性模型的规范。这些规范是声明性的，这大大简化了我们的形式化开发。尽管如此，如 [12] 所示，这些规范相当于某些操作规范，接近于实现。
定义 1
事务 T, S, … 是一对 $(E, \ltpo)$，其中 $E \subseteq \Event$ 是具有不同标识符的有限非空事件集，程序顺序 $\ltpo$ 是 E 上的全序。历史 H 是具有不相交事件标识符集的事务的有限集。带注释的历史 $(H, \level)$ 是一对，其中 H 是历史，$\level: H \to \set{\SER, \perp}$。执行是三元组 $X = ((H, \level), \lthb, \ltar)$，其中 $(H, \level)$ 是带注释的历史，$\lthb$ 是 H 上的严格偏序，$\ltar$ 是 H 上的全序，且满足 $\lthb \subseteq \ltar$。我们称 $\lthb$ 为 先行发生关系（happens-before），称 $\ltar$ 为 仲裁（arbitration）。
我们将执行的组件表示为 X.H，并对类似的结构使用相同的符号。
事务记录了一组操作以及客户端程序调用它们的顺序。历史记录了在有限的数据库计算中提交的事务。为了简化，我们省略了对已中止和进行中的事务以及无限数据库计算的处理。带注释的历史通过一个函数 $\level$ 丰富了历史，该函数记录了程序员请求在可串行化条件下执行的事务，以及在底层数据库提供的弱一致性模型下执行的事务。最后，执行通过先行发生关系和仲裁顺序丰富了带注释的历史，这些关系以声明的方式表示了内部数据库的处理过程。直观上，$T \lthb S$ 表示 S 知道 T 执行的更新，因此 S 中操作的结果可能取决于 T 的效果。我们称那些没有先行发生关系的事务为并发（concurrent）。关系 $T \ltar S$ 表示 S 写入的对象版本取代了 T 写入的版本。约束 $\lthb \subseteq \ltar$ 确保事务 T 写入的数据版本不会被 T 知道的写入所取代。
我们使用集合 $\set{\CC, \PC, \PSI, \SI, \SER}$ 来表示我们在第 1 节（Section 1）中处理的一致性模型，并且我们通过 wm 遍历这个集合。在图 4 中，我们指定了这些一致性模型，作为图 3 中公理的组合，以约束执行。形式上，我们令由一致性模型 wm 允许的带注释历史集由 $\hist(wm) = \set{(X.H, X.\level) \mid X \models wm}$ 给出。现在我们解释这些公理以及它们（不）允许的异常。我们在图 2 中总结了这些异常。
给定一个全序 < ⊆ A × A 和一个集合 B ⊆ A，我们写作 max (B,<) 表示元素 b ∈ B，使得 ∀a ∈ B.a ≤ b；如果 A = ∅，则 max (B,<) 未定义。我们以显而易见的对偶方式定义 min 。在下文中，当我们写 max (B,<) 或 min (B,<) 时，我们假设它们是已定义的。给定一个偏序 < ⊆ A × A 和元素 a ∈ A，我们定义 a 的下集（downset）为 $\before(a, \lt) = \set{a' \in A \mid a' \lt a}$，并令 $\before(a, \lt, op\ x) = \before(a, \lt) \cap \set{a' \in A \mid a' \Vdash op(x, \_)}$。
内部一致性公理（$\Int$）确保在一个事务中，数据库提供顺序语义：在事务 $(E, \ltpo)$ 中，对象 x 上的读取事件 e 返回 e 之前在 x 上发生的最后一个事件的值。由集合 $\before(e, \ltpo, \_x)$ 给出的事件。在 $(E, \ltpo)$ 中，如果读取 e 之前没有在同一对象上（即 $\before(e, \ltpo, \_x) = \emptyset$）的操作，那么它的值由其他事务的写入决定，使用外部一致性公理（$\Ext$）。为了形式化 $\Ext$，我们将 ⊢ 符号扩展到事务的操作。对于给定的事务 $T = (E, <_{\po})$，对象 $x \in \Obj$ 和自然数 n ∈ ℕ，我们写作：
- $T \vdash \write(x, n)$ 当且仅当 $, <_{}) \write(x, n) $；
- $T (x, n) $ 当且仅当 ${e E | e _(x,_) }, <_{}) (x, n) $。
根据 $\Ext$，如果一个事务 T 在对对象 x 进行写操作之前对其进行了读操作，那么这个读操作返回的值由那些在 T 之前发生并且写入了 x 的事务决定；这些事务的集合由 $\before(T,\lthb, \write x)$ 给出。如果这个集合是空的，那么 T 读取初始值 0；否则，它读取由 $\ltar$ 中的最后一个事务写入的值。$\Ext$ 保证了事务的原子可见性（atomic visibility）：一个事务的所有写入操作要么全部对另一个事务可见，要么全不可见。关于此问题的详细讨论可参见 [12] 第 3 节。
$\SER$ 公理形式化了应用程序员要求以串行化方式执行的事务所提供的附加保证，这些要求记录在 $\level$ 中。我们将在后文详细讨论此公理；现在我们假设对所有执行来说 $\level = (λT.\bot)$。
公理 $\Int$、$\Ext$ 和 $\SER$ 定义了因果一致性（$\CC$） [22]。它禁止了图 2(a) 中所示的因果性违背异常（causality violation anomaly），在该异常中，一个用户看到了评论内容，但没有看到与该评论相关联的图书。这一异常被禁止是因为 $\lthb$ 是传递的，因此必须有 $T_1 \lthb T_3$。由于 $T_1 \ltar T_2$，T2 的写入覆盖了 T1 的写入，因此 $\Ext$ 推导出 $T_3 (y, review) $ 和 $T_3 (x, book) $。
因果一致性允许丢失更新异常（lost update anomaly），如图 2(b)
所示。该异常可能由程序 ViewItem
和 StoreBid
产生，前者允许用户查询某物品的信息，后者允许用户对物品进行出价操作。它们访问一张
ITEMS
表，其中的行代表物品，并包含主键 iId、物品描述
desc
和当前出价数 nbids。图
2(b) 中的异常由两次 StoreBid
调用产生，它们分别生成了事务 T1 和 T2，目的是增加某物品的出价数。这两个事务读取了物品的初始出价数（即
0），并发地修改了它，导致其中一次更新被丢失。此结果由第三个事务 T3（由 ViewItem
生成）观察到。丢失更新异常由公理 Conflict
禁止，该公理保证更新相同对象的事务不能并发执行。此公理排除了图 2(b)
中的执行历史。我们通过加强因果一致性并引入 Conflict
公理来定义并行快照隔离（parallel snapshot isolation, $\PSI$） [26]。这种一致性模型允许出现图 2(c)
所示的长分叉异常（long fork anomaly），该异常在第 1 节中讨论过。
我们通过使用公理 $\Prefix$
来加强因果一致性（$\CC$）和并行快照隔离（$\PSI$），从而定义前缀一致性（prefix
consistency, $\PC$） [11]
和快照隔离（snapshot isolation, $\SI$）
[6]。$\Prefix$ 公理的含义是：如果事务
T 观察到了事务 S，那么它也必须观察到所有在 $\ltar$ 中位于 S
之前的事务，这一性质使用关系的顺序组合 ; 来形式化。$\Prefix$ 公理禁止了图 2(c)
中的执行历史：T1 和
T2 必须通过 $\ltar$ 相关联；但若如此，要么 T4 必须观察到 Alice，要么
T3 必须观察到 Bob。与因果一致性一样，前缀一致性允许出现图
2(b) 中的丢失更新异常。快照隔离禁止了丢失更新，但允许图 2(d)
所示的写偏差异常（write skew anomaly）。此异常可能由 RegUser
生成的执行产生，图 1 中的对象 x 和 y 分别对应于 USERS
表的不同行。RegUser
的两次调用生成了未能看到彼此写入的事务，结果是两位用户使用了相同的昵称并同时注册成功。
Dynamic Robustness Criteria
我们的第一个目标是定义标准来检查我们考虑的一致性模型之一中的单个执行 X 是否具有可序列化历史记录：$X.H \in \hist(\SER)$。从这些动态稳健性标准中，在下一节中，我们将得出静态标准来检查给定应用程序的所有执行是否都是这种情况。
我们的动态标准是基于依赖图来制定的，这在数据库文献中被广泛使用 [2]。设标签集 L 定义如下：$D = \{(\wr, x), (\ww, x) | x \in \Obj\}, L = D \cup \{(\rw, x) | x \in \Obj\}$。我们使用 λ 来表示 L 中的元素，并用 s, t 表示 L* 的元素。一个图 G 是一个有序对 (H,→)，其中 H ∈ Hist，且 → ⊆ H × L × H。我们用 $T \overset{\lambda}{\longrightarrow} S \in G$ 来表示 (T,λ,S) ∈ →。我们还使用一些图论的概念。图 G 中的路径 π 是一系列非空有限边的序列 $T_0 \overset{\lambda_0}{\longrightarrow} T_1 \overset{\lambda_1}{\longrightarrow} \ldots \overset{\lambda_{n-1}}{\longrightarrow} T_n$。在这种情况下，我们写作 π ∈ G。如果 T0 = Tn，则该路径是一个环；如果路径上所有其他事务对都是不同的，则它是一个简单循环。我们还写作 $T \overset{\lambda}{\longrightarrow} S \in \pi$ 来表示边 $T \overset{\lambda}{\longrightarrow} S$ 出现在路径 π 中。
给定一个图 G = (H,→)，我们用 s→+ 表示最小关系，使得：
- 如果 $T \overset{\lambda}{\longrightarrow} S \in G$，则 $T \overset{\lambda}{\longrightarrow}^+ S$；
- 如果 $T \overset{\lambda}{\longrightarrow} T_0 \in G$，并且存在某个 T′ ∈ H 使得 $T' \overset{s}{\longrightarrow}^+ S$，则 $T \overset{\lambda s}{\longrightarrow}^+ S$。
我们用 $\overset{s}{\longrightarrow}^*$ 表示 $\overset{s}{\longrightarrow}^+$ 的自反闭包，因此对于每个 T ∈ H，都有 $T \overset{\varepsilon}\longrightarrow^* T$。现在我们定义一个将执行映射到依赖图的映射。
定义 2 依赖图
执行 $X = ((H, \_), \lthb, \ltar )$ 的动态依赖图是 $\DDG(X) = (H, \longrightarrow)$，其中对于每个 $x \in \Obj$，→ 包含了下列三元组：
- 读依赖：$T \overset{\wr, x}{\longrightarrow} S$，若 $S \vdash \read(x, \_)$ 并且 $T = \max(\before(S, \lthb, \write \ x), \ltar)$；
- 写依赖：$T \overset{\ww, x}{\longrightarrow} S$，若 $T \vdash \write(x, \_), S \vdash \write(x, \_)$ 并且 $T \ltar S$；
- 反向依赖：$T \overset{\rw, x}{\longrightarrow} S$ 若 T ≠ S 并且满足以下的一个条件：
- $T \vdash \read(x, \_), S \vdash \write(x, \_)$ 并且 $\before(T, \lthb, \write \ x) = \emptyset$；
- $\exist T' \in H. T' \overset{\wr, x}{\longrightarrow} S \land T' \overset{\ww, x}{\longrightarrow} S$。
引理 3
对于每个 X，若 X 满足 $\Int$ 和 $\Ext$ 公理（这意味着 X 符合 $\RA$），且 $\DDG(X)$ 无环，则 $X.H \in \hist(\SER)$。
定义 4 执行的关键环
给定一个执行 X，某个边 $T \overset{\lambda}{\longrightarrow} S \in \DDG(X)$ 是不被保护的，若 $X.\level(T) \ne \SER$ 或 $X.\level(S) \ne \SER$。T0, T1, …, Tn（其中 T0 = Tn）包含某个简单无弦且 rw-最小的环 $\pi \in \DDG(X)$ 是：
- CC-critical：若 π 包含两个未被保护的边 $T_i \overset{\rw, \_}{\longrightarrow} T_{i+1}$ 和 $T_j \overset{\lambda}{\longrightarrow} T_{j+1}$，其中 i ≠ j 且 $\lambda \in \set{(\ww, \_), (\rw, \_)}$；
- PC-critical：若 π 包含一个未被保护的边 $T_i \overset{\rw, \_}{\longrightarrow} T_{i+1}$ 和至少两个相邻的未被保护的标记属于 $\set{(\ww, \_), (\rw, \_)}$ 边；
- PSI-critical：若
- π 包含至少两个未被保护的 $\rw$ 边，并且；
- 对每个 $T_i \overset{\rw, x}{\longrightarrow} T_{i+1}, T_j \overset{\rw, y}{\longrightarrow} T_{j+1} \in \pi$，若 i ≠ j，则 x ≠ y；
- SI-critical：若
- π 包含至少两个相邻的未被保护的 $\rw$ 边，并且；
- 对每个 $T_i \overset{\rw, x}{\longrightarrow} T_{i+1}, T_j \overset{\rw, y}{\longrightarrow} T_{j+1} \in \pi$，若 i ≠ j，则 x ≠ y。
图 2 中的执行图（级别为 (λT.⊥)）包含关键环：（c）包含一个 PSI 关键环，（d）包含一个 SI 关键环。
定理 5
对于每个 wm 和 X，如果 X ⊨ wm，则 $\DDG(X)$ 包含一个环，当且仅当它包含一个 wm 关键环。
根据定理 5 和引理 3，我们得到我们的动态鲁棒性标准。
推论 6 动态鲁棒性充分条件（其实也是充要条件）
对于每个 wm 和每个 X，如果 X ⊨ wm 且 $\DDG(X)$ 不包含任何 wm 关键环，则 $X.H \in \hist(\SER)$。
我们注意到，上述 SI 鲁棒性标准是现有标准的一个变体 [16, 15]。在我们的设置中，它只是我们新标准的一个结果。
为了证明定理 5，我们展示图 3 中的公理如何影响依赖图中的边和路径的性质。首先，观察到 wr、ww 边与路径之间的关系。对于每个 X 和每个 T, S ∈ X.H，定义确保：
$$ T \overset{\wr}{\longrightarrow} S \in \DDG(X) \Rightarrow T \lthb S\\ $$
$$ (T \overset{\wr}{\longrightarrow} S \in \DDG(X) \lor T \overset{\ww}{\longrightarrow} S \in \DDG(X)) \Rightarrow T \ltar S\\ $$
$$ X \models \Conflict \land T \overset{\ww}{\longrightarrow} S \in \DDG(X) \Rightarrow T \lthb S $$
这些蕴含关系使我们得以证明，在某些条件下，如果两个事务在依赖图中通过路径连接，它们也通过发生前关系或仲裁相互关联。
引理 7
对于任意 X，s ∈ L+，且 $T \overset{s}{\longrightarrow}^{+} S \in \DDG(X)$，如果 $X \models \SerTotal$，则：
- 如果所有 $\rw$ 和 $\ww$ 边在 $T \overset{s}{\longrightarrow}^{+} S$ 中受到保护，则 $T \lthb S$；
- 如果所有 $\rw$ 边在 $T \overset{s}{\longrightarrow}^{+} S$ 中受到保护，则 $T \ltar S$；
- 如果 $X \models \Conflict$ 并且所有 $\rw$ 边在 $T \overset{s}{\longrightarrow} S$ 中受到保护，则 $T \lthb S$。
接下来的引理表明，如果 $T \overset{\rw,x}{\longrightarrow} S$，则 T 不能发生在 S 之前：在这种情况下，T 必须读取至少与 S 写入的值相同或更新的值，这与反依赖的定义相矛盾。
引理 8 $$ \forall X, \forall x \in \Obj, \forall T, S \in X.H.T \overset{\rw,x}{\longrightarrow} S \in \DDG(X) \implies S \not\le_{hb} T \land T \vdash \read(x,\_) \land S \vdash \write(x, \_) $$
定理 5 证明
该命题的“如果”蕴含关系是显而易见的，因此让我们证明“当且仅当”的含义。假设图 $\DDG(X)$ 包含一个循环 π′。从 π′ 我们可以很容易地构建一个循环：
$$ \pi = T_0 \overset{\lambda_0}{\longrightarrow} T_1 \overset{\lambda_1}{\longrightarrow} \ldots \overset{\lambda_{n-1}}{\longrightarrow} T_n, (\text{where } T_0 = T_n, n \geq 2) $$
在 $\DDG(X)$ 中，该循环是简单的、无弦的且 $\rw$ 最小的。该论证是案例分析关于 wm 的。我们考虑 CC 和 PSI，并推迟完整证明到 [7]。
从依赖图推导执行
在 CONCUR’16 原文中：
- ≀ 边意味着 $\lthb$ 关系；
- $\Conflict$ 公理下的 $\ww$ 边意味着 $\lthb$ 关系；
- $\wr \cup \ww$ 边意味着 $\ltar$ 关系；
对于 $\rw$ 边，我们能得到的限制只有：
定理 α
在 $\SerTotal$ 公理约束下，被保护的 $\rw$ 边意味着 $\ltar$ 和 $\lthb$；
定理 7 实际上是这一命题利用 $\lthb$ 的传递性得到的引理。
如果对 $\level=(\SER)$ 的事务的限制从 $\SerTotal$ 强化为 SER-(2)，定理 α 仍然成立。其他性质在表格第 4 列。
| RA | Update Atomic | SI | SER | protected edge （$\SerTotal$） |
$T_1[wm]
\longrightarrow T_2[\SER]$ （by SER-(2)） |
$T_1[wm] \longrightarrow T_2[\SI]$ | |
|---|---|---|---|---|---|---|---|
| ≀ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ |
| $\ww$ | $\ltar$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ | $\lthb$ |
| $\rw$ | none | none | none | $\lthb$ | $\lthb$ | none | none |
Static Robustness Criteria
我们现在说明如何将动态鲁棒性标准（推论 6）提升为静态标准，这使得程序员能够分析其应用程序的行为，并可作为静态分析工具的基础。
我们通过一组事务程序 fi 来定义应用程序 A，并给出其事务代码：A = {f1, …, fn}（例如，参见图 1）。按照数据库文献 [16] 中的标准，这从应用程序逻辑的其余部分中抽象出来，以专注于直接与数据库交互的部分。我们将程序对 I = (f, v) 和其实际参数向量称为程序实例。应用程序实例 I 是一组程序实例，带注释的应用程序实例是一对 (I, levelS)，其中 levelS : I → {SER, ⊥} 定义程序员请求在可序列化下执行哪些程序。我们首先制定检查特定带注释的应用程序实例的稳健性的标准，该标准是通过使用给定参数运行一组事务程序得出的。然后，我们概述了如何将这些标准推广到整个应用程序。
我们旨在以最简单的形式说明将动态稳健性标准提升为静态稳健性标准的想法。为此，我们从编程语言的语法中抽象出来，并假设我们只给出了每个事务程序读取或写入的对象集的近似信息。也就是说，我们假设一个函数 rwsets 将每个程序实例 I 映射到三元组 rwsets(I) = (R3, W3, W2)。非正式地说，R3 和 W3 是可能在 I 的某些执行中读取或写入的所有对象的集合，而 W2 是必须在 I 的任何执行中写入的对象的集合，但前提是 W2 ⊆ W3。例如，对于 I = (StoreBid,hiId1, 7i)（图 1），我们有
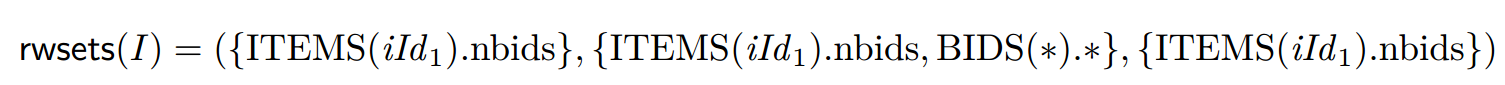
其中 ∗ 表示“所有字段”或“所有行”。
为了形式化读/写集的含义，我们定义了一个关系，该关系确定是否可以由给定的 I 生成历史记录。我们让 T I 对于 rwsets(I) = (R3, W3, W2)，如果：
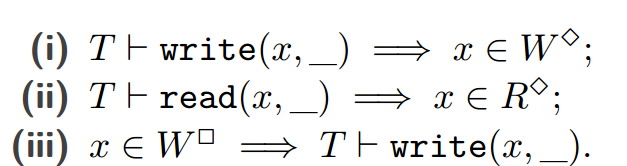
我们将 与带注释的历史和带注释的应用实例的关系提升：
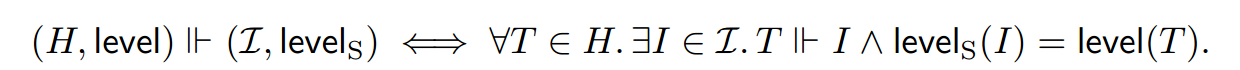
定义 9 静态依赖图
图 6 显示了 (3) 中 I 的静态依赖图。非正式地，静态依赖图 SDG(I) 的边描述了由 I 产生的执行中事务之间可能存在的依赖关系：边 I λ > J 表示可能存在的依赖关系，边 I λ ←→ J 表示必须存在的依赖关系。正式地，给定一个带注释的应用程序实例 (I, levelS)，我们说对 (DDG(X), X.level) 被对 (SDG(I), levelS) 过度近似，写为 (DDG(X), X.level) (SDG(I), levelS)（即，前者是后者的子图），如果对于某个总函数 f : X.H → I 我们有：
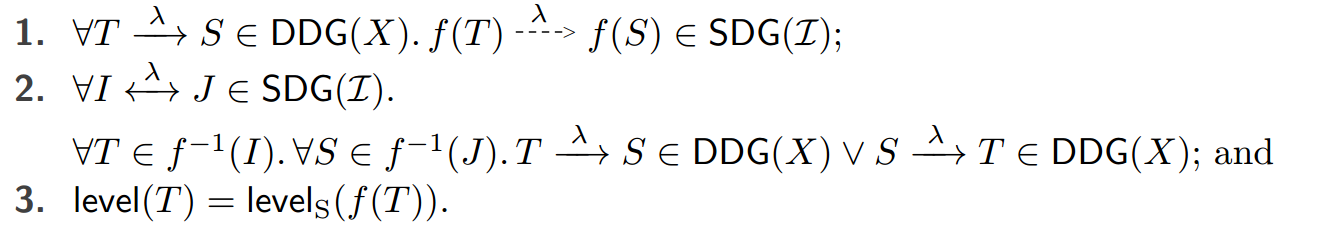
引理 10 $$ \forall X . \forall (\I, \level_S).(X.H, X.\level) \Vdash (\I, \level_S) \Rightarrow (\DDG(X), \level) \triangleleft (\SDG(\I), \level_S) $$
我们现在通过使用与动态依赖图相同的路径和循环概念来制定静态鲁棒性标准（第 3 节）。给定一对 (I, levelS) 和程序实例 I0, I1, . . . , In（其中 I0 = In）中 π ∈ SDG(I) 中的一个循环。
定义 11 程序实例的关键环
对于一对 $(\I, \level_S)$，若 $\level_S(I_i) \ne \SER$ 或 $\level_S(I_{i+1}) \ne \SER$，则称 $I_i \overset{\lambda}{\dashrightarrow} I_{i+1} \in \SDG(\I)$ 是未被保护的。一个环 $\pi \in \SDG(\I)$ 包括 I0, I1, …, In（其中 I0 = In）是：
- CC-critical：若 π 包含两条未被保护的边 $I_i \overset{\rw, \_}{\dashrightarrow} I_{i+1}, I_j \overset{\lambda}{\dashrightarrow} I_{j+1}$，其中 i ≠ j 并且 $\lambda \in \set{(\ww, \_), (\rw, \_)}$；
- PC-critical：若 π 包含一个未被保护的边 $I_i \overset{\rw, \_}{\dashrightarrow} I_{i+1}$ 和至少两个相邻的未被保护的标记属于 $\set{(\ww, \_), (\rw, \_)}$ 边；
- PSI-critical：若
- π 包含至少两个未被保护的 $\rw$ 边，并且；
- 对每个 $I_i \overset{\rw, x}{\dashrightarrow} I_{i+1}, I_j \overset{\rw, y}{\dashrightarrow} I_{j+1} \in \pi$，若 i ≠ j，则 x ≠ y；
- SI-critical：若
- π 包含至少两个相邻的未被保护的 $\rw$ 边，并且；
- 对每个 $I_i \overset{\rw, x}{\dashrightarrow} I_{i+1}, I_j \overset{\rw, y}{\dashrightarrow} I_{j+1} \in \pi$，若 i ≠ j，则 x ≠ y。
请注意，与动态依赖图中的关键循环（定义 4）不同，静态图中的关键循环不必是简单的。以下引理指出 ⊲ 保留了关键循环。
定理 12
对每个 $(G, \level), (F, \level_S)$ 和 wm，使得 $(G, \level) \triangleleft (F, \level_S)$，若 G 包含 wm-critical 环，则 F 包含 wm-critical 环。
换言之，若 F 不包含 wm-critical 环，则 G 不包含 wm-critical 环。该关系是单向的。
定理 13 静态鲁棒性充分条件
对每个 $(H, \level), (\I, \level_S)$ 和 wm，若 $\SDG(\I)$ 不包含 wm-critical 环并且 $(H, \level) \in \hist(wm)$，则若 $(H, \level) \Vdash (\I, \level_S)$，我们有 $H \in \hist(\SER)$。
- 静态鲁棒性充分条件：若程序 $\I$ 满足某条件，则 $\I$ 产生的所有历史 $H \in \hist(\SER)$；反之，若 $\I$ 不满足这些条件，则不能保证所有 $H \in \hist(\SER)$；
- 程序鲁棒性充要条件：若程序 $\I$ 满足某条件，则 $\I$ 产生的所有历史 $H \in \hist(\SER)$；反之，若 $\I$ 不满足这些条件，则保证并非所有 $H \in \hist(\SER)$。
如果在定理 13 的基础上，能构造出某个反例 $(H, \level) \Vdash (\I, \level_S)$ 但 $H \not \in \hist(\SER)$，则充分条件上升为充要条件。
Analysing Whole Applications
定理 13 中的静态标准允许程序员分析给定应用程序实例的鲁棒性。使用定理完整分析应用程序需要考虑其无限数量的实例，这项任务最好由自动静态分析工具完成。我们现在概述如何使用抽象解释 [13, 25] 中的想法来有限地表示和分析应用程序的所有实例集。在未来，这可以为在静态分析工具中自动化我们的鲁棒性标准铺平道路。由于篇幅限制，我们仅通过示例介绍这些概念。
Related Work
在数据库环境中，应用程序鲁棒性最早是由 Fekete 等人 [16] 研究的，他们提出了针对快照隔离 (SI) 的鲁棒性标准 [6]。然后，Fekete 将该标准扩展到 SI 数据库，允许程序员为某些事务请求可序列化性 [15]，我们也考虑了这种机制。我们的标准的制定方式与 Fekete 等人的类似，使用依赖图 [2]。然而，与他们的工作相比，我们考虑了更微妙的并行快照隔离、前缀一致性和因果一致性模型，这些模型允许比 SI 更多的异常。我们使用的方法也不同于 Fekete 等人的方法。他们考虑了 SI 的操作规范 [6]，这使得鲁棒性标准的证明高度复杂。相比之下，我们可以从使用声明性规范中受益，通过利用事务的原子可见性 [12] 实现简洁性。这使我们能够更系统地提出鲁棒性标准。
还研究了在常见多处理器和编程语言的弱共享内存模型上运行的应用程序的鲁棒性（例如 [9]）。然而，这方面的工作尚未考虑使用事务的应用程序。事务使一致性模型语义复杂化，这使得建立鲁棒性标准更具挑战性。
应用程序中事务的可序列化性简化了其正确性属性的建立，但对此并非必要。因此，建立应用程序正确性的另一种方法是直接证明其所需属性，而不要求事务仅产生可序列化的行为。Lu 等人 [23] 为 ANSI SQL 隔离级别和 SI 提出了相应的方法，Gotsman 等人 [18] 为 PSI 和其他一些最新模型提出了相应的方法。这些方法是我们的补充：它们所需的条件可以被更多应用程序满足，但比健壮性更难检查。
Conclusion
在本文中，我们迈出了理解最近提出的大型数据库事务一致性模型对使用它们的应用程序的正确性属性的影响的第一步。为此，我们提出了检查使用弱一致性模型的应用程序何时仅表现出强一致性行为的标准。这使程序员能够检查应用程序的正确性是否会因选择特定的一致性模型或要在可序列化下执行的事务而得到保留。
Fekete 等人对 SI 的鲁棒性结果此前已催生出用于静态检测应用程序中异常的自动工具 [19]。我们的工作可以为提供较弱一致性模型的数据库的类似进展奠定基础。我们的动态鲁棒性标准也具有独立意义：除了作为静态分析的基础外，此类标准还可用于优化运行时监控算法 [24, 28]。
在建立鲁棒性标准时，我们采用了一种利用公理规范的系统方法 [12]：使用一致性模型的公理，我们表征了模型执行依赖图中允许的循环，并利用这些表征提供了可靠的静态分析技术。我们希望这种方法可以适用于针对大型数据库提出的其他一致性模型。
