$$ \def\po{\mathsf{\textcolor{red}{po}}} \def\so{\mathsf{\textcolor{purple}{so}}} \def\soo{\mathsf{\textcolor{purple}{soo}}} \def\wr{\mathsf{\textcolor{teal}{wr}}} \def\ww{\mathsf{\textcolor{red}{ww}}} \def\rw{\mathsf{\textcolor{blue}{rw}}} \def\co{\mathsf{\textcolor{orange}{co}}} \def\SO{\mathsf{\textcolor{purple}{SO}}} \def\WR{\mathsf{\textcolor{teal}{WR}}} \def\CM{\mathsf{\textcolor{orange}{CM}}} \def\CO{\mathsf{\textcolor{brown}{CO}}} \def\AR{\mathsf{\textcolor{pink}{AR}}} \def\vis{\mathsf{\textcolor{orange}{vis}}} \def\VIS{\mathsf{\textcolor{orange}{VIS}}} \def\hb{\mathsf{\textcolor{pink}{hb}}} \def\hbo{\mathsf{\textcolor{pink}{hbo}}} \def\A{\mathsf{A}} \def\E{\mathsf{E}} \def\cc{\mathsf{cc}} \def\ec{\mathsf{ec}} \def\sc{\mathsf{sc}} \def\rc{\mathsf{rc}} \def\mav{\mathsf{mav}} \def\rr{\mathsf{rr}} \def\sameobj{\mathsf{sameobj}} \def\oper{\mathsf{oper}} \def\txn{\mathsf{txn}} \def\sametxn{\mathsf{sametxn}} \def\withdraw{\mathtt{withdraw}} \def\deposit{\mathtt{deposit}} \def\getBalance{\mathtt{getBalance}} \def\heta{\hat{\eta}} \def\RYW{\mathbf{RYW}} \def\MR{\mathbf{MR}} \def\MW{\mathbf{MW}} \def\WFR{\mathbf{WFR}} $$
摘要
面向用户的在线服务采用地理分布的数据存储来减少延迟并容忍部分故障，以提供快速且始终可用的体验。然而，地理分布并非没有代价；应用程序开发者需要处理弱一致性行为，并且缺乏构建高级复制数据类型的抽象机制，这导致了复杂的应用程序逻辑，并不可避免地将不一致性暴露给用户。一些商业分布式数据存储和多个学术提案提供了一致性级别的层次结构，更强的一致性保证会带来更高的延迟和吞吐量成本。然而，正确为操作分配合适的一致性级别需要细致的推理，并且通常是一个容易出错的任务。
在本文中，我们提出了 QUELEA，一种针对最终一致性的数据存储（ECDS）的声明式编程模型，它配备了一种契约语言，能够指定细粒度的应用层一致性属性。一个契约执行系统分析这些契约，并自动生成受保护方法所需的一致性协议。我们在一个现成的支持无协调事务的 ECDS 之上实现了 QUELEA。通过包括两个大型网络应用在内的几个基准测试，展示了我们的方法的有效性。
关键词：最终一致性、可用性、CRDT、公理合约、合约分类、分布式事务、SMT 求解器、可判定逻辑、Quelea、Cassandra、Haskell
作者：
- KC Sivaramakrishnan*, University of Cambridge, UK, sk826@cl.cam.ac.uk
- Gowtham Kaki, Purdue University, USA, gkaki@cs.purdue.edu
- Suresh Jagannathan, Purdue University, USA, suresh@cs.purdue.edu
Introduction
许多现实世界的网络服务（例如由 Amazon、Facebook、Google、Twitter 等公司构建和维护的网络服务）在数据中心内和数据中心之间跨多个副本复制应用程序状态和逻辑。复制不仅旨在提高应用程序吞吐量并减少用户感知的延迟，而且还旨在容忍部分故障而不损害整体服务可用性。
传统上，程序员依靠强一致性保证（例如线性化 [15] 或可序列化 [22]）来构建正确的应用程序。虽然强一致性是一种容易表述的属性，但它掩盖了大规模分布式系统在非均匀延迟、可用性和网络分区方面的现实 [8, 14]。事实上，旨在提供“始终在线”体验的现代网络服务绝大多数都倾向于可用性和分区容忍度而不是强一致性。为此，已经提出了几种弱一致性模型，例如最终一致性、因果一致性、会话保证和时间线一致性。
在弱一致性下，开发人员需要注意并发的冲突更新，并且必须小心谨慎以避免不必要的不一致（例如，银行账户余额为负数，或购物车中出现已移除的商品 [13]）。通常，这些不一致会从应用程序中泄露出来并被用户看到。最终，开发人员必须决定适合特定操作的一致性级别；可以理解，这是一个容易出错的过程，需要对应用程序以及底层数据存储的语义和实现有复杂的了解，而这些通常只有非正式的描述。尽管如此，选择正确的一致性级别不仅对正确性至关重要，而且对应用程序的可扩展性也至关重要。虽然选择比要求的更弱的一致性级别可能会引入程序错误和异常，但选择比必要更强的一致性级别可能会对程序的可扩展性和性能产生负面影响。
弱一致性还会阻碍程序的组合推理。尽管应用程序可能自然地以易于理解和富有表现力的数据类型（如 map、树、queue 或 graph）来表达，但地理分布式存储通常仅提供一组最小的数据类型，并带有内置冲突解决策略，如最后写入者获胜（LWW）寄存器、计数器和集合 [17, 26]。此外，虽然传统数据库系统通过事务实现可组合性，但地理分布式存储通常缺乏对数据的无限制可序列化事务访问。因此，在这种环境中工作需要适当地强制应用程序状态仅使用存储的功能来运行。
为了解决这些问题，我们描述了 QUELEA，一种用于 ECDS 的声明式编程模型和实现。QUELEA 的主要创新之处在于它是一种表达性合约语言，用于声明和验证细粒度的应用程序级一致性属性。程序员使用契约语言公理化地指定允许在复制数据类型上执行的合法执行集。
契约是使用原始一致性关系（例如可见性和会话顺序）以及标准逻辑和关系运算符构建的。契约执行系统将数据类型上的操作静态映射到存储上可用的特定一致性级别，并可证明地验证映射的正确性。本文做出了以下贡献：
- 我们引入了 QUELEA，这是 Haskell 的浅层扩展，支持对 ECDS 中发现的复制数据类型的描述和验证。契约用于指定细粒度的应用程序级一致性属性，并进行静态分析以将最有效和最合理的存储一致性级别分配给相应的操作。
- QUELEA 支持任意数据类型上的无协调事务。我们扩展了我们的契约语言以表达细粒度事务隔离保证，并利用契约执行系统自动为事务分配正确的隔离级别。
- 我们提供元理论来证明我们的合同执行系统的健全性，并确保只有在满足一致性的必要条件时才执行操作。
- 我们描述了 QUELEA 的实现，它是 Cassandra [17]（一种著名的通用数据存储）上的透明垫片层。对一组真实世界的应用程序（包括类似 Twitter 的微博网站和类似 eBay 的拍卖网站）进行的实验评估说明了我们的方法的实用性。
本文的其余部分安排如下。下一节介绍系统模型。我们描述了最终一致性下编程的挑战，并在 $\S 3$ 中介绍了 QUELEA 合约作为克服这些问题的建议解决方案。$\S 4$ 提供了有关合约语言及其到存储一致性级别的映射的更多细节，以及用于证明映射正确性的元理论。$\S 5$ 介绍了交易合约及其分类。$\S 6$ 描述了在 Cassandra 之上 QUELEA 的实现。$\S 7$ 讨论了实验评估。$\S 8$ 和 $\S 9$ 介绍了相关工作和结论。
System Model
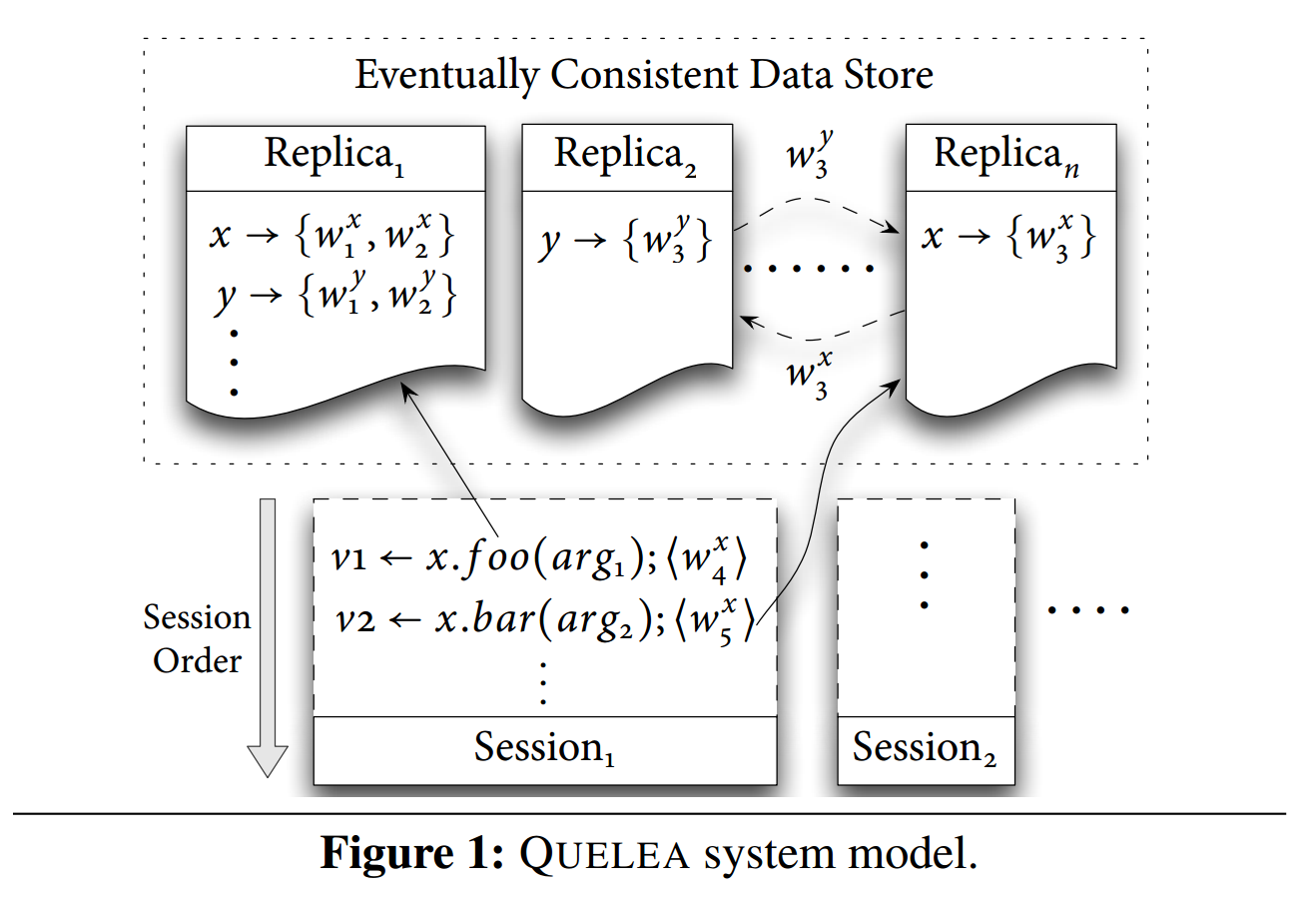
在本节中，我们将描述系统模型，并介绍我们的契约语言所基于的基本关系。图 1 展示了我们系统模型的示意图。分布式存储由一组副本组成，每个副本存储一组对象（x、y 等）。我们假设每个对象在存储中的所有副本上都有复制。一个对象在任何副本上的状态是由对该对象执行的所有更新（效果）组成的集合。例如，在副本 1 上 x 的状态是由对 x 执行的效果 w1x 和 w2x 组成的集合。
每个对象都关联着一组操作。客户端通过调用对象上的操作与存储进行交互。特定客户端在存储上的一系列操作称为会话。通常，大量的客户端（因此也有许多会话）并发地访问数据存储。重要的是，客户端不知道某个操作被应用到了哪个副本；为了最小化延迟、负载均衡等原因，数据存储可以选择将操作路由到任意副本。例如，同一会话在同一对象上调用的 foo 和 bar 操作，可能会最终被应用到不同的副本上，因为当客户端调用 bar 时，foo 被应用到的副本 1 可能无法访问。
当在副本 1 上对对象 x 调用 foo 操作并带有参数 arg1 时，它只是对该副本上该对象当前的效果集（w1x 和 w2x）进行归约，产生结果 v1 发送回客户端，并发出一个新的单一效果 w3x ，该效果被附加到副本 1 上 x 的状态中。因此，每个操作都是在其被调用的对象状态的一个快照上进行评估的。在这种情况下，效果 w1x 和 w2x 对 w3x 是可见的，逻辑上表示为 $\vis(w_1^x, w_3^x) \land \vis(w_2^x, w_3^x)$ ，其中 $\vis$ 是效果之间的可见性关系。可见性是一种非自反且不对称的关系，只涉及同一个对象上操作产生的效果。执行只读操作类似，只是不会产生新的效果。添加到特定副本的效果会被异步发送到其他副本，并最终合并到所有其他副本中。请注意，此模型不假定针对并发冲突更新的特定解决策略，而是保留了每一个更新。当操作在一个特定副本上对一个对象的效果集进行归约时，更新冲突就会得到解决。
两个来自同一会话的效果 w4x 和 w5x 被认为是在会话顺序中（逻辑上表示为 $\so(w_4^x, w_5^x)$ ）。会话顺序是一种非自反、传递的关系。来自对相同对象 x 的操作的效果 w4x 和 w5x 被认为是处于相同对象关系下，写作 $\sameobj(w_4^x, w_5^x)$ 。最后，我们可以使用关系 $\oper$ 将每个效果与其生成操作相关联。在当前例子中，$\oper(w_4^x, foo)$ 和 $\oper(w_5^x, bar)$ 成立。为了简化起见，我们假设所有对象上的所有操作名称都是唯一的。
这个模型包含了与最终一致性相关的所有不一致性。这项工作的目标是为每个操作确定精确的一致性级别，以确保应用程序级约束不被违反（与鲁棒性相一致）。在下一节中，我们将具体描述在 ECDS 之上构建一致银行账户的相关挑战。随后，我们将说明我们的契约和规范语言如何利用基本关系 $\vis$、$\so$、$\sameobj$ 和 $\oper$ 来缓解这些挑战。
Motivation
考虑一下我们如何在 ECDS 上实现高可用性银行账户，并具有完整性约束，即余额必须为非负数。我们首先在 QUELEA 中实现银行账户复制数据类型（RDT），然后描述获得所需正确性保证的机制。
RDT Specification
QUELEA 的一个关键创新之处在于它允许向存储添加新的 RDT，这样就无需强制应用程序逻辑来利用存储提供的数据类型。此外，QUELEA 将数据类型的收敛语义（即如何解决冲突更新）与其一致性属性（即更新何时可见）分开处理。这种关注点分离允许对冲突解决进行操作推理，对一致性进行声明性推理。这些技术的结合增强了存储的可编程性。
我们假设银行账户对象提供三种操作：存款 deposit、取款
withdraw 和获取余额
getbalance，并假设如果账户余额不足，取款将失败。QUELEA
中的每个操作都属于以下类型，以 Haskell 语法编写：
1 | |
操作采用效果列表（该对象的更新历史记录）和输入参数，并返回结果以及可选效果（只读操作不返回任何内容）。新效果（如果发出）将添加到当前副本的对象状态中，并异步发送到其他副本。QUELEA 中的银行帐户操作的实现如图 2 所示。
数据类型 Acc 表示银行帐户的效果类型。函数
sum 返回列表中元素的总和，sel1
返回元组的第一个元素。对于每个操作，hist
是某个副本中对象状态的快照。从这个意义上讲，RDT
上的每个操作都是原子的，因此适合顺序推理。在这里，getBalance
是一个只读操作，deposit 总是发出效果，而
withdraw
仅在帐户中有足够的余额时才会发出效果。我们以这种风格用几十行代码实现了大量用于现实基准的
RDT，包括购物车、拍卖和微博网站等。
Summarization
请注意，getBalance
的定义减少了对帐户的整个更新历史记录。如果我们要实现此银行帐户 RDT
的有效实施，我们需要帐户历史记录的摘要。直观地说，当前帐户余额总结了帐户的状态。具有历史记录
[Deposit 10, Withdraw 5]
的银行帐户明显等同于具有单个存款操作 [Deposit 5]
的银行帐户；我们可以用后者替换较早的历史记录，而商店的客户将无法分辨两者之间的区别。
这种可观察等价性的概念也可以推广到其他
RDT。例如，具有多次更新的最后写入者获胜寄存器等效于仅具有最后一次写入的寄存器。类似地，具有添加和删除操作集合的集合等效于具有从原始集合中添加一系列活动元素的集合。由于可观察等价性的概念特定于每个
RDT，因此程序员可以提供一个汇总函数 - 类型为 [e] -> [e]
- 作为 RDT 规范的一部分。银行账户的汇总函数为：
1 | |
给定一个银行账户历史记录，汇总函数将返回一个新的历史记录，其中包含当前账户余额的单笔存款。我们的实现调用与 RDT 关联的汇总函数来减少副本维护的效果集的大小。
Anomalies under Eventual Consistency
我们的目标是为每个银行账户操作选择正确的一致性级别，以便 (1)
余额保持非负数，以及 (2) getBalance
操作永远不会错误地返回负余额。
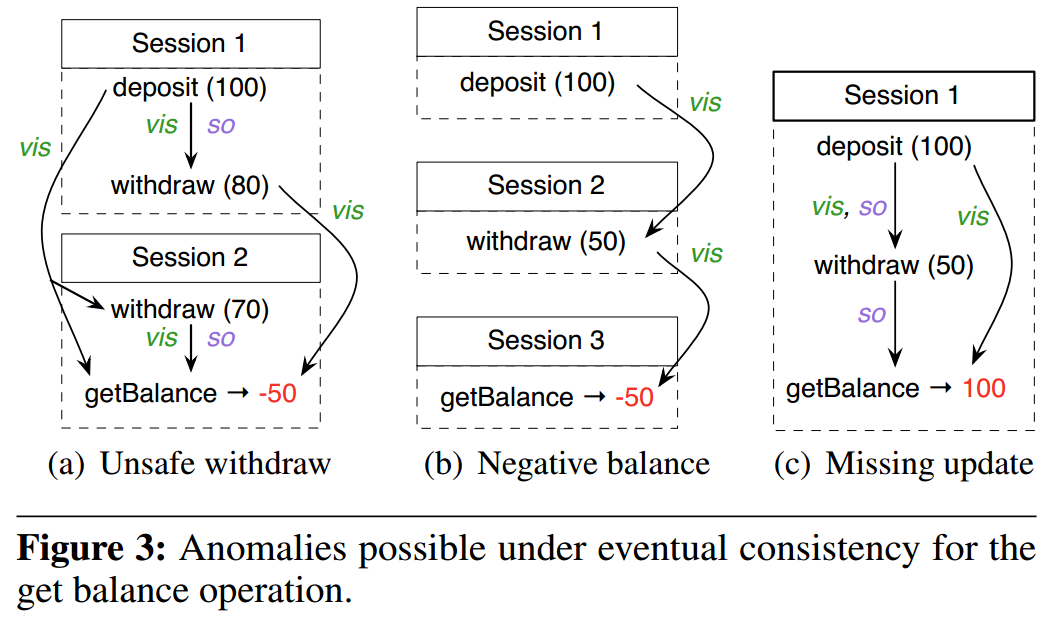
考虑图 3(a)
中所示的执行。假设图中的所有操作都在同一个银行账户对象上进行，初始余额为零。会话
1 执行了一笔 100 的存款，随后在同一会话中执行了一笔 80
的取款。取款操作见证了存款并成功完成。随后，会话 2
执行了一笔取款操作，但重要的是，由于最终一致性，它只见证了会话 1
的存款，而没有见证随后的取款。因此，这笔取款也错误地成功了，违反了完整性约束。随后的
getBalance
操作，如果见证了所有之前的操作，将报告一个负余额。
很容易看出，防止并发取款操作可以消除这种异常。这可以通过坚持取款操作作为强一致性操作来实现。尽管进行了这种强化，getBalance
操作仍然可能错误地向用户报告一个负余额。考虑图 3(b)
中所示的执行，它由三个并发会话组成，分别执行存款、取款和
getBalance 操作，都在同一个银行账户对象上。如
vis 边所示，会话 2 中的取款操作 withdraw(50)
见证了会话 1 中存款 deposit(100)
的效果，得出余额充足，并成功完成。然而，getBalance
操作可能只见证了这次成功的取款，而没有见证因果前的存款，并向用户报告负
50 的余额。
在最终一致性下，用户还可能暴露于其他形式的不一致性。图 3(c)
显示了一个执行，其中会话中的 getBalance
操作没有见证同一会话中较早执行的取款操作的效果，可能是因为它是由一个尚未合并
withdraw 效果的副本提供的。此异常会导致用户错误地认为
withdraw 操作失败。
虽然很容易理解上述异常发生的原因，但找到适当的修复方法却并不容易。使
getBalance
成为强一致性操作肯定足以避免异常，但这真的有必要吗？考虑到强制执行强一致性的成本
[25,
28]，除非没有可行的替代方案，否则最好避免施加如此严格的条件。探索这些替代方案的空间需要了解各种弱一致性替代方案在语义上的细微差别。
Contracts
QUELEA 通过让程序员声明应用程序级别的一致性约束作为合约（图 4）来帮助将操作映射到适当的一致性级别，这些合约公理化地指定了涉及该操作的允许执行集。在银行账户的情况下，任何不表现出前一节描述的异常的执行都是银行账户对象上的良好执行。通过指定每种数据类型的操作调用跟踪的合法执行集，QUELEA 确保该类型的所有执行都是良好范式的。
在我们的运行示例中，很明显，为了保持关键的完整性约束，withdraw
操作必须是强一致性的。也就是说，给定两个 withdraw 操作
a 和 b，要么 a 对 b
可见，要么反之亦然。我们表达这一应用程序级别的强一致性要求为
withdraw 的合约 (ψw)：
$$ \psi_{w} = \forall (a : \withdraw). \sameobj(a, \heta) \Rightarrow a = \heta \lor \vis(a, \heta) \lor \vis(\heta, a) $$
这里，$\heta$ 代表
withdraw 操作发出的效果。语法 $a
: \withdraw$ 表示 a
是由 withdraw 操作发出的效果，即 $\text{oper}(a, \withdraw)$
成立。合约规定，如果当前操作发出效果 $\heta$，那么对于任何由 withdraw
操作发出的操作 a，要么 $a = \heta$，要么 a 对 $\heta$
可见，或者反之亦然。任何在银行账户对象上执行的操作，如果保持上述
withdraw 操作的合约，则认为是从 withdraw
的正确实现派生的。
为了防止 getBalance 操作永远显示负余额，有必要防止图
3(b) 中描绘的情景。设 $\heta$ 代表
getBalance 操作发出的效果。如果 withdraw
操作的效果 (b) 对 $\heta$ 可见，且 deposit
操作的效果 (a) 对
withdraw 操作的效果 (b) 可见，那么必须是 a 也对 $\heta$
可见。一个精确捕捉这一应用程序级别一致性要求的 getBalance
合约 (ψgb1)
可以这样写：
$$ \psi_{gb}^1 =\forall (a : \deposit), (b : \withdraw). (\vis(a, b) \land \vis(b, \heta) \Rightarrow \vis(a, \heta)) $$
为了防止图 3(c) 中描述的缺失更新异常，银行账户上的
getBalance
操作必须见证同一会话中在同一银行账户上执行的所有先前
deposit 和 withdraw
操作的效果。我们可以表达一个额外的 getBalance 合约 (ψgb2)，以捕捉这一一致性要求：
$$ \psi_{gb}^2 = \forall (c : \deposit \lor \withdraw). (\so \cap \sameobj)(c, \heta) \Rightarrow \vis(c, \heta)) $$
我们的合约语言提供了用于组合关系的运算符。语法 (R1∩R2)(a,b) 等价于 R1(a,b) ∧ R2(a,b)。
上述合约 (ψgb2)
表示，如果在会话顺序中，存款或取款操作在 getBalance
操作之前执行，并且在与 getBalance 操作相同的对象上应用，则
getBalance 操作必须见证这些前置操作的效果。
getBalance 操作的最终合约 (ψgb)
仅仅是前两个版本 (ψgb1
和 ψgb2)
的合取：
$$ \psi_{gb} = \forall (a : \deposit), (b : \withdraw), (c : \deposit \lor \withdraw). \\ (\vis(a, b) \land \vis(b, \heta) \Rightarrow \vis(a, \heta)) \\ \land ((\so \cap \sameobj)(c, \heta) \Rightarrow \vis(c, \heta)) $$
直观上，这一规范禁止了图 3(b) 和 3(c) 中描述的
getBalance 异常的发生。
最后，由于对存款操作何时或如何执行没有限制，其合约简单为真。
From Contracts to Implementation
请注意，withdraw 和 getBalance
的合约仅表达应用程序级别的一致性要求，并不涉及底层存储的语义。编写合约时，程序员只需考虑在
QUELEA
系统模型下的应用程序语义。应用程序级别一致性要求到适当的存储级别保证的映射是自动在后台完成的。如何确保执行符合合约？挑战在于合约提供了一个声明性的（公理化的）执行规范，而需要的是一个操作过程来强制执行其隐含的约束。
一种策略是投机性地（speculatively）执行操作。在这里，操作在接收到客户端或其他副本时暂时应用。我们可以维护执行的运行时表现，并在运行时检查良好形成条件，如果执行不良好则回滚。然而，状态维护的开销和用户定义合约的复杂性可能会使这种技术在实践中不可行。
我们设计了一种静态方法。合约在定理证明器的帮助下进行分析，并静态地映射到特定的存储级别一致性属性，该证明器保证保留合约语义。我们称此过程为合约分类。鉴于存储级别一致性属性的多样性和复杂性，系统实现者通过在相同的合约语言中描述存储语义来参数化分类过程，该语言与用于表达操作合约的语言相同。在下一节中，我们将详细介绍合约语言，并描述针对特定存储语义的分类过程。
Contract Language
Syntax
我们的核心合约语言的语法如图 4 所示。该语言基于一阶逻辑 (FOL)，并允许对类型化和非类型化效应变量进行前缀全称量化。我们使用特殊效应变量（$\heta$）来表示当前操作——正在编写合约的操作。
请注意，在契约中 $\heta$
是自由变量。我们在分类契约时（$\S
4.4$）确定其作用域。一个效果的类型仅仅是引发该效果的操作的名称（例如：withdraw）。我们允许在类型中使用析取，以让效果变量覆盖多个操作名称。契约
∀(a:τ1∨τ2). ψ
仅仅是语法糖，表示 $\forall a. (\oper(a,
\tau_1) \lor \oper(a, \tau_2)) \Rightarrow
\psi$。一个未类型化的效果变量覆盖所有操作名称。
在我们的契约语言中，量化自由命题是谓词表达的效果变量对之间的关系的合取、析取和蕴含。谓词关系的语法类以原始的 $\vis$，$\so$，和 $\sameobj$ 关系为基础，并且也接受可以表示为原始关系的并、交或传递闭包的派生关系。常用的派生关系是同一对象会话顺序（$\soo = \so \cap \sameobj$），发生在之前的顺序（$\hb = (\so \cup \vis)^+$）和同一对象发生在之前的顺序（$\hbo = (\soo \cup \vis)^+$）。
Semantics
QUEUELA 契约是程序执行的公理定义上的约束。图 5 总结了定义公理执行的相关工件。我们将公理执行形式化为一个元组 $(\A, \vis, \so, \sameobj)$，其中 $\A$，称为效果汤（effect soup），是在程序执行期间生成的所有效果（版本）的集合，而 $\vis, \so, \sameobj \subseteq \A \times \A$ 分别是可见性、会话顺序和同一对象关系，这些关系在运行时被观察到。
请注意，公理执行（$\E$）的定义为契约公式中自由出现的原始关系（例如：$\vis$）提供了解释，并且将量化域固定为程序执行期间观察到的所有效果（$\A$）的集合。因此，$\E$ 是任何可以用我们的契约语言表达的一阶公式（ψ）的潜在模型。如果 $\E$ 确实是 ψ 的有效模型（表示为 $\E \models \psi$），我们说执行 $\E$ 满足契约 ψ：
定义 1
一个公理执行 $\E$ 满足契约 ψ 当且仅当 $\E \models \psi$。
Capturing Store Semantics
我们的契约语言的一个重要方面是它能够捕获存储级一致性保证以及应用程序级一致性要求。与 [10] 类似，我们可以严格定义各种存储语义，包括结合任何会话子集和因果关系保证以及多个一致性级别的语义。但是，为了我们的目的，我们确定了三个特定的一致性级别——最终一致性、因果一致性和强一致性，许多分布式存储通常提供这三个级别，具有可调（tunable）一致性，但延迟和可用性方面的开销会增加。
Eventual consistency
只要客户端可以访问至少一个副本，就可以满足最终一致性操作。在银行账户示例中，存款是最终一致性操作。虽然 ECDS 通常提供具有所有可能异常的基本最终一致性，但我们假设我们的存储提供了更强大的语义，可以保持高可用性 [2, 19]；存储始终公开更新的因果关系。可以根据以下合约定义正式捕获此语义：
$$ \psi_\ec = \forall a, b. \; \hbo(a, b) \land \vis(b, \heta) \Rightarrow \vis(a, \heta) $$
上述契约规定，如果因果关系上继 a 之后的某个效应 b 对 $\heta$ 也可见，则效应 a 必须对当前效应 $\heta$ 可见。因此，如果每个存储副本始终维护并向客户端公开更新的因果关系，那么这样的存储将满足此契约。在这样的系统中，只要某个副本可访问，就可以满足最终一致性操作（例如存款）的保证，这需要比存储提供的保证更弱的保证。
Causal consistency
因果一致的操作需要看到对象状态的一个因果一致的快照，包括在同一会话中执行的动作。后一个要求意味着，如果来自同一会话的两个操作
o1 和 o2 被应用到不同的副本
r1 和 r2
上，第二个操作不能被执行，直到 o1 的效果被包含在 r2
中。getBalance
操作需要因果一致性，因为它要求来自同一会话的操作必须是可见的，这在最终一致性下无法保证。相应的存储语义由以下定义的契约
$\psi_\cc$ 捕捉：
$$ \psi_\cc = \forall a. \; \hbo(a, \heta) \Rightarrow \vis(a, \heta) $$
Strong consistency
强一致的操作在网络分区下可能会无限期地阻塞。一个例子是对
withdraw 操作的全序契约。相应的存储语义由以下定义的契约
$\psi_\sc$ 捕捉：
$$ \psi_\sc = \forall a. \; \sameobj(a, \heta) \Rightarrow \vis(a, \heta) \lor \vis(\heta, a) \lor a = \heta $$
Contract Classification
我们的目标是将应用级别的操作一致性约束映射到适当的存储级别一致性保证，这些保证能够满足这些约束。在我们的契约语言中，能够表达这两种约束作为契约，使我们能够比较并确定一个操作（op）的契约（ψop）是否足够弱，以至于在由契约 ψst 标识的存储一致性级别下能够被满足。为此，我们定义了一个二元的“弱于”关系，用于我们的契约语言，如下所示：
定义 2
一个契约 ψop 被称为弱于 ψst（表示为 ψop ≤ ψst），当且仅当 Δ ⊢ ∀η̂.ψst ⇒ ψop。
在该蕴含式中的量化符绑定在 ψst 和 ψop 中自由出现的 η̂。蕴含式的上下文（Δ）是一组关于原始关系性质的假设的合取。一个形式良好的公理执行（$\E$）应该满足这些假设（即，$\E \models \Delta$）。
定义 3
一个公理执行 $\E = (\A, \vis, \so, \sameobj)$ 是形式良好的，如果以下公理（Δ）成立：
- $\hbo$ 顺序关系是无环的：$\forall a. \neg \hbo(a, a)$；
- $\vis$ 仅关联同一对象上的操作：$\forall a, b. \vis(a, b) \Rightarrow \sameobj(a, b)$；
- $\so$ 是一个传递关系：$\forall a, b, c. \so(a, b) \land \so(b, c) \Rightarrow \so(a, c)$；
- $\sameobj$ 是一个等价关系：
- $\forall a. \sameobj(a, a)$；
- $\forall a, b. \sameobj(a, b) \Rightarrow \sameobj(b, a)$；
- $\forall a, b, c. \sameobj(a, b) \land \sameobj(b, c) \Rightarrow \sameobj(a, c)$。
如果操作的契约 ψop 弱于存储契约 ψst，则前者表达的约束被后者提供的保证所隐含。一阶逻辑的完备性使我们能够断言，任何满足 ψst 的形式良好的执行（$\E$）也满足 ψop（即，$\E \models \psi_{op}$）。因此，在由 ψst 捕获的存储一致性级别下执行操作 op 是安全的。
观察到契约 $\psi_{\sc}$，$\psi_{\cc}$ 和 $\psi_{\ec}$ 本身在 ≤ 关系下是全序的：$\psi_{\ec} \leq \psi_{\cc} \leq \psi_{\sc}$。这符合直觉，即任何在 $\psi_{\ec}$ 或 $\psi_{\cc}$ 下可满足的契约在 $\psi_{\sc}$ 下也是可满足的，任何在 $\psi_{\ec}$ 下可满足的契约在 $\psi_{\cc}$ 下也是可满足的。我们感兴趣的是最弱的保证（在 $\psi_{\ec}$，$\psi_{\cc}$，和 $\psi_{\sc}$ 中）以满足契约。我们定义相应的一致性级别为契约的一致性级别。
分类方案在图 6
中正式给出，定义了判断契约一致性级别的规则。例如，方案将
getBalance 契约（ψgb）从
$\S 3$ 分类为因果一致契约，因为蕴含式
$\Delta \vdash \forall \heta. \psi_{\cc}
\Rightarrow \psi_{gb}$ 在一阶逻辑中是有效的（因此，$\psi_{gb} \leq \psi_{\cc}$），而蕴含式 $\Delta \vdash \forall \heta. \psi_{\ec} \Rightarrow
\psi_{gb}$ 是无效的（因此，$\psi_{gb}
\nleq
\psi_{\ec}$）。由于我们将契约语言限制为逻辑的可判定子集，因此这些蕴含式的有效性可以机械地决定，使我们能够在
QUELEA 中自动化分类方案。
除了将契约分类为一致性级别的三个简单规则外，分类方案还提供了一个判断契约是否形式良好的规则。契约是形式良好的当且仅当它在 $\psi_{\sc}$ 下是可满足的——存储可以提供的最强一致性保证。否则，它被认为是不形式良好的，并被静态地拒绝。
Generality of Contracts
值得注意的是，我们的契约语言提供了一种通用方法来捕获应用程序级一致性属性，并且不依赖于特定的存储语义。特别是，相同的应用程序级契约可以轻松映射到具有不同一致性格的不同存储。为了说明这一点，让我们考虑 Terry 等人 [27] 提出的基于会话保证的一致刻画。Terry 等人提出了以下四个无法比较的会话保证，其语义在以下契约中捕获：
$$ \text{Read Your Writes (RYW)} \coloneqq \forall a. \soo(a, \heta) \Rightarrow \vis(a, \heta) \\ \text{Monotonic Reads (MR)} \coloneqq \forall a, b. \vis(a, b) \land \soo(b, \heta) \Rightarrow \vis(a, \heta) \\ \text{Monotonic Writes (MW)} \coloneqq \forall a, b. \soo(a, b) \land \vis(b, \heta) \Rightarrow \vis(a, \heta) \\ \text{Writes Follow Reads (WFR)} \coloneqq \forall a, b, c. \vis(a, b) \land \vis(c, \heta) \land (\soo \cup =)(b, c) \Rightarrow \vis(a, \heta) $$
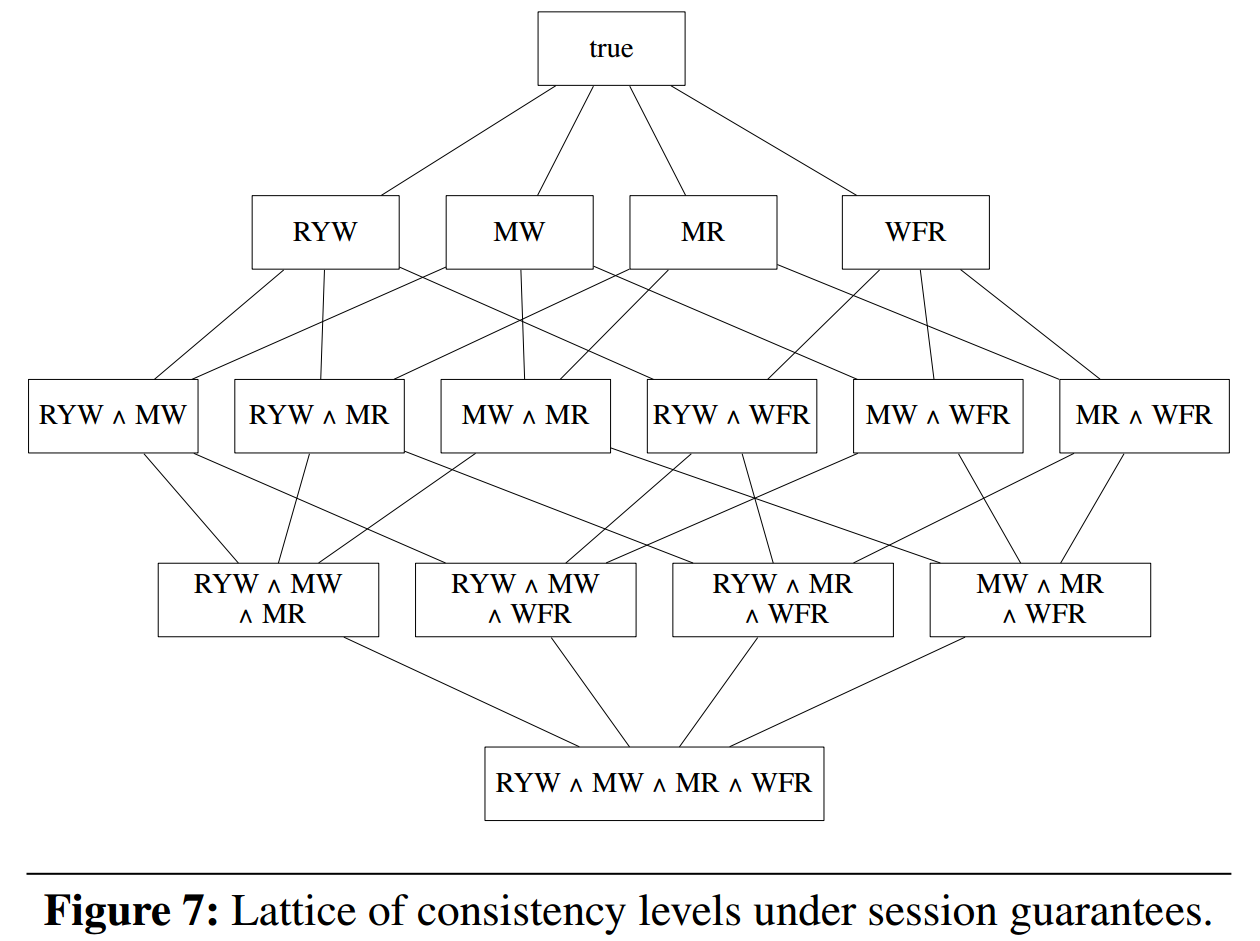
在该方案中，操作的一致性级别是上述保证的任意组合，它们形成图 7
所示的部分有序一致性格。该格中的每个元素对应于一个存储一致性级别，并由其契约表示。从上级元素到下级元素的边对应于相应契约之间的弱于关系。根据该方案对契约进行分类是在格中进行定向搜索，从底部开始，确定可以满足契约的最弱一致性级别。确定在最弱的一致性级别下契约可以被满足。根据这个方案，deposit
操作不需要任何保证，getBalance 需要 $\RYW$ 和 $\WFR$（$\psi_{gb}
\leq \RYW \land \WFR$），而 withdraw
不能被满足（$\psi_{w} \nleq \RYW \land \MW
\land \MR \land \WFR$）。
Soundness of Contract Classification
Operational Semantics
Soundness of Operational Semantics
Transaction Contracts
虽然针对单个操作的合约提供了程序员对象级别的声明式推理，但现实场景中经常涉及跨越多个对象的操作。为了解决这个问题，最近的几个系统 [2, 9, 26] 提出了最终一致的事务，以便组合多个对象上的操作。然而，考虑到经典的事务模型（如可串行性和快照隔离）需要跨副本协调，这些系统提倡在网络分区下仍可用的无协调事务（coordination-free transactions），但仅提供较弱的隔离保证。无协调事务具有复杂的一致性语义和广泛变化的运行时开销。与操作级别的一致性类似，选择正确的事务类型的责任在于程序员。这一选择进一步被单个操作的一致性语义所复杂化。
Syntax and Semantics Extensions
QUELEA
自动化了选择正确和最有效的事务隔离级别的过程。类似于针对单个操作的合约，程序员将合约与事务关联，声明式地表达一致性规范。我们扩展了合约语言，在无量词命题下引入了一个新的术语
$\txn \ S_1 \ S_2$，其中 S1, S2
是效果集合，并引入了一个新的原始等价关系
sametxn，该关系对来自同一事务的效果有效。$\txn\set{a, b}\set{c, d}$ 只是 $\sametxn(a, b) \land \sametxn(c, d) \land \lnot
\sametxn(a, c)$ 的语法糖，其中 a 和 b 被认为属于当前事务。
我们假设不属于任何事务的操作属于它们自己的唯一事务。虽然事务可能具有不同的隔离保证，但我们假设所有事务都提供原子性。因此，我们在 Δ 中包含以下公理：
$$ \forall a, b, c. \, \txn\set{a}\set{b, c} \land \sameobj(b, c) \land \vis(b, a) \Rightarrow \vis(c, a) $$
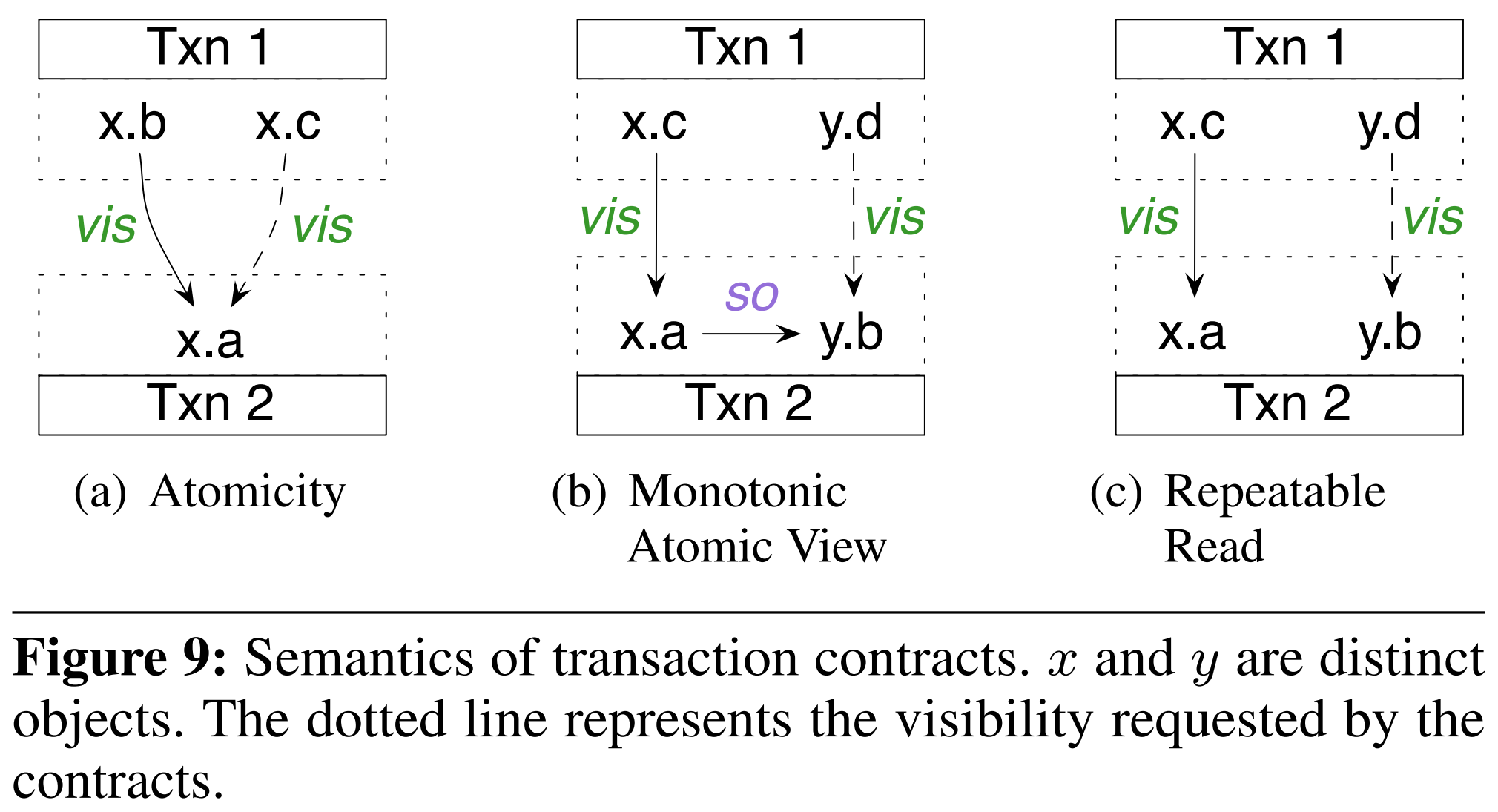
该原子性实际上保证了 $(\VIS, \AR)$ 框架的 Read Atomic。
该合约的语义如图 9(a) 所示。
Transactional Bank Account
为了说明声明式推理对于事务的实用性，考虑我们运行示例的扩展，使用两个账户（对象）——当前账户
(c) 和储蓄账户 (s)。每个账户提供
withdraw、deposit 和 getBalance
操作，具有之前定义的相同合约。我们考虑两个事务——save(amt)，将
amt 从当前账户转移到储蓄账户，以及
totalBalance，返回各个账户余额的总和。我们的目标是确保
totalBalance 返回的对象状态一致快照的结果。QUELEA
代码如下：
ψsv 和
ψtb
是对应事务的契约。函数 classify
静态地将这些契约分配到存储提供的事务隔离级别之一；$()
是元编程语法，用于将结果拼接到程序中。atomically
构造在给定的隔离级别 x
上调用封闭的操作，确保操作的效果以原子方式可见。
虽然使两个事务可序列化可以确保正确性，但分布式存储很少提供可序列化的事务，因为它们的可用性要求和可扩展性的含义
[2]。幸运的是，这些事务可以通过更弱的隔离保证来满足。然而，尽管事务提供了原子性，异常仍然可能发生。例如，在
totalBalance 事务中，两个 getBalance
操作可能由不同的副本提供服务，每个副本有一组不同的已提交的
save 事务。如果第一个（第二个） getBalance
操作见证了第二个（第一个） getBalance 操作未见证的
save
事务，那么返回的余额将小于（大于）实际余额。如何选择最弱的隔离保证以防止这种异常并不立即明显。
相反，QUELEA
要求程序员简单地将一致性要求作为契约声明。由于我们希望两个
getBalance 操作见证同一组 save 事务，我们定义
totalBalance 事务的约束 ψtb
如下：
$$ \psi_{tb} = \forall a : \getBalance, b : \getBalance, \\ (c : \withdraw \lor \deposit), (d : \withdraw \lor \deposit). \\ \txn\{a, b\}\{c, d\} \land \vis(c, a) \land \sameobj(d, b) \Rightarrow \vis(d, b) $$
上述定义中的关键思想是 txn
原语允许我们将不同对象上的操作关联起来。
save
事务只需要确保它执行的两个写操作以原子方式可见。由于这通过将它们组合在一个事务中来保证，save
不需要任何额外的约束，因此 ψsv
简单地为真。
Coordination-free Transactions
为了说明事务契约分类的实用性，我们识别了三种广为人知的无协调事务语义——已提交读取（RC）[7]、单调原子视图（MAV）[2] 和可重复读取（RR）[7]，并说明了分类策略。我们的技术确实可以应用于不同的隔离级别格。
具有 ANSI RC 语义的事务仅见证已提交的操作。假设一个副本将缓冲事务更新，直到同一事务的所有更新都可用。一旦事务的所有更新都可用，缓冲的更新将对后续的客户端请求可见。这确保了事务的原子性。重要的是，RC 不包含任何其他保证。因此，实现 RC 的存储不需要副本间的协调。我们可以将 RC 表达如下：
$$ \psi_\rc = \forall a, b, c. \txn\{a\}\{b, c\} \land \sameobj(b, c) \\ \land \vis(b, a) \Rightarrow \vis(c, a) $$
请注意，上述定义与 $\S 6.1$
中描述的事务原子性保证相同。save 操作是一个 RC
事务的例子。
MAV 语义确保如果事务 $ T_1 $ 中的某个操作见证了另一个事务 $ T_2 $ 的效果，那么 $ T_1 $ 中的后续操作也将见证 $ T_2 $ 的效果。MAV 语义对于维护外键约束、物化视图和二级更新的完整性非常有用 [2]。为了实现 MAV，存储只需跟踪运行事务见证的事务集 $ S_t $，并在某个副本上执行操作之前，确保该副本包含了 $ S_t $ 中的所有事务。因此，MAV 是无协调的。MAV 语义通过以下契约捕获：
$$ \psi_\mav = \forall a, b, c, d. \txn\set{a, b}\set{c, d} \land \so(a, b) \land \vis(c, a) \\ \land \sameobj(d, b) \Rightarrow \vis(d, b) $$
其语义如图 9(b) 所示。
ANSI RR
语义要求事务见证数据存储状态的快照。重要的是，这个快照可以从任何副本中获得，因此
RR 也是无协调的。一个这样的事务的例子是 totalBalance
事务。RR 语义通过以下契约捕获：
$$ \psi_\rr = \forall a, b, c, d. \txn\{a, b\}\{c, d\} \land \vis(c, a) \\ \land \sameobj(d, b) \Rightarrow \vis(d, b) $$
其语义如图 9(c) 所示。
Classification
类似于操作级别的契约，在 ≤ 关系下，这里描述的无协调事务语义形成了一个全序：$\psi_\rc \leq \psi_\mav \leq \psi_\rr$。事务分类也类似于图 6 中展示的操作级别契约分类；给定一个事务上的契约 ψ，我们从最弱的事务契约 $\psi_\rc$ 开始，并逐步将其强度与已知的事务契约进行比较，直到找到一个可以安全解除 ψ 的隔离级别。否则，我们报告一个类型错误。
Implementation
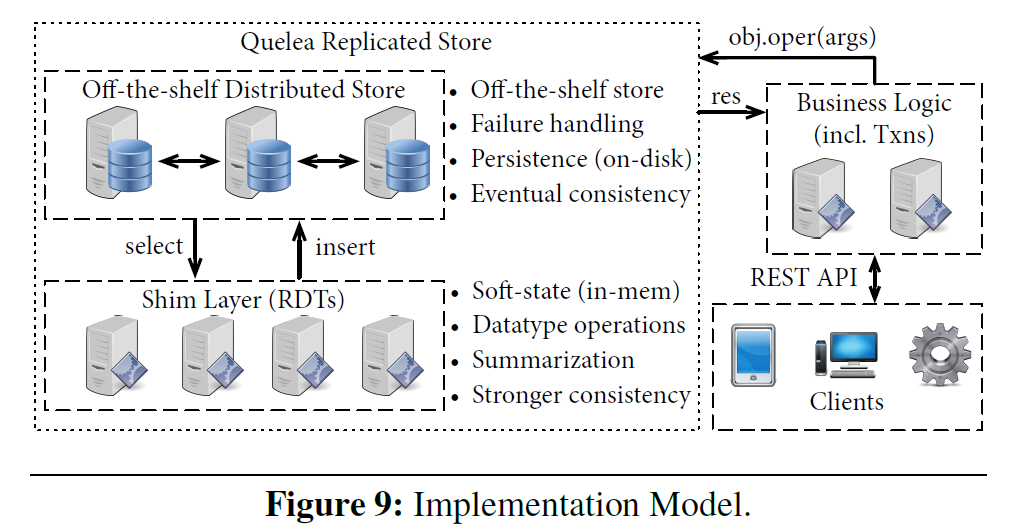
QUELEA 实现为 GHC Haskell 的浅层扩展，并在 Cassandra 上运行，Cassandra 是一个现成的最终一致性分布式数据（或备份）存储，负责所有数据管理问题（即，复制、容错、可用性和收敛性）。使用 Template Haskell 实现静态合约分类，借助 Z3 [31] SMT 解决器来完成证明义务。图 9 展示了整体系统架构。
复制的数据类型和各种一致性语义在 shim 层实现和强制执行。我们的实现支持数据类型操作的最终一致性、因果一致性和强一致性，以及事务的 RC、MAV 和 RR 语义。此功能完全基于 Cassandra 暴露的标准接口实现。从工程角度来看，利用现成的数据存储使实现仅包含大约 2500 行 Haskell 代码，这些代码被封装为一个库。
Operation Consistency
垫片层通过显式跟踪由于可见性、会话和相同事务关系而引入的影响之间的依赖关系，维护后备存储中对象子集的因果一致的内存快照。依赖关系跟踪类似于 [3] 和 [21] 中介绍的技术。由于 Cassandra 提供持久性、收敛性和容错性，因此每个垫片层节点仅充当软状态缓存，没有节点间通信，并且可以随时安全终止。同样，可以根据需求生成新的垫片层节点。
