SAT & SMT

约束求解问题

给定一组约束，求：

• 这组约束是否可满足
• （可选）如果可满足，给出一组赋值
• （可选）如果不可满足，给出一个较小的矛盾集 unsatisfiable core

总的来说是不可判定的问题，但存在很多可判定的子问题：

如：

$$(a>10)\wedge (b<100\vee b>200)\wedge (a+b=30)$$

可满足：$a=15,b=15$

• SAT solver：解著名的 NP 完全问题
• Linear solvers：求线性方程组
• Array solvers：求解包含数组的约束
• String solver：求解字符串约束
• SMT：综合以上各类约束求解工具

SAT 问题描述

SAT 解法

SAT 基本求解算法-穷举

Sat(assign) {
	if (assign 是完整的) {
		if (每个子句中都有至少一个文字为真) {
			return true;
		} else {
			return false;
		}
	} else {
		选择一个未赋值的变量 x;
		return sat(assign ∪ {x = 0}) || sat(assign ∪ {x = 1});
	}
}

时间复杂度：最差为 $O(2^n)$。

优化 1：冲突检测

Sat(assign) {
	if (assign 有冲突) {
        return false;
    }
	if (assign 是完整的) {
        return true;
	}
    选择一个未赋值的变量 x;
    return sat(assign ∪ {x = 0}) || sat(assign ∪ {x = 1});
}

相当于及时剪枝，比穷举法略好。

优化 2：赋值推导

标准推导方法 DPLL

• Unit Propagation：其他文字都为假，剩下的一个文字必定为真
• Unate Propagation：当一个子句存在为真的文字时，可以从子句集合中删除
• Pure literal elimination：当一个变量只有为真或者只有为假的形式的时候，可以把包含该变量的子句删除

dpll(assign) {
	assign' = 赋值推导(assign);
	if (assign' 有冲突) {
		return false;
	}
	if (assign' 是完整的) {
		return true;
	}
	选择一个未赋值的变量 x;
	return dpll(assign’ ∪ {x = 0}) || dpll(assign’ ∪ {x = 1});
}

该算法被称为 DPLL ，由，由 Davis, Putnam, Logermann, Loveland 在 1962 年代提出

高级推导方法

• Probing：如果 x=0 或者 x=1 都能推导出 y=0 ，则推导出 y=0
• Equivalence classes：预先检查出等价的子句集合（如仅仅是顺序不同），然后删除其中一个

优化 3：变量选择 Branching Heuristics

• 基于子句集的：
  • 优先选择最短子句里的变量
  • 优先选择最常出现的变量
• 基于历史的：
  • 优先选择之前导致过冲突的变量
  • 注意：变量选择只是在下一次选择变量时生效，对于已经生成的搜索树仍然会遍历结束

优化 4 ：冲突导向的子句学习 CDCL

Conflict Driven Clause Learning 基本思想：在搜索过程中学习问题的性质，加入约束集合中

一个 DPLL 的例子

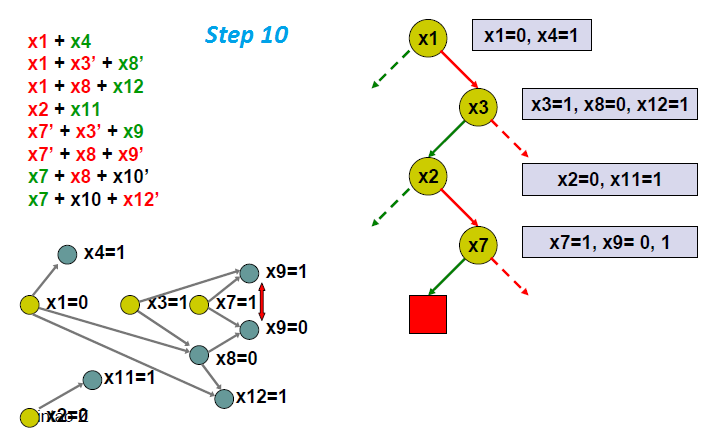
CDCL：子句学习

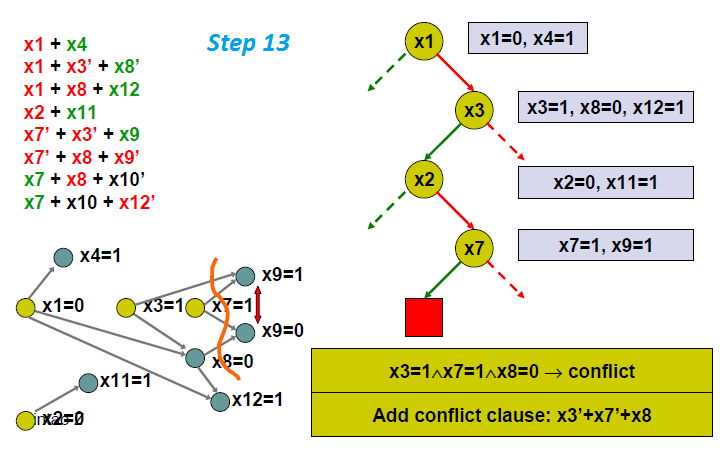
• 在搜索过程中发现矛盾，找到最小的矛集合，把这一集合加入到子句集合当中。
• 注意从新添加约束出发的推导实际保证了之前探过的冲突赋值不会出现
• 所以不再需要记录之前遍历过的赋值，每次任意选择剩下的变量和赋值即可
• 空赋值推出冲突意味着 UNSAT。

cdcl() {
	assign = 空赋值;
	while (true) {
		赋值推导(assign);
		if (推导结果有冲突) {
			if (assign为空) {
				return false;
			}
			添加新约束;
			撤销赋值;
		} else {
			if (推导结果是 完整的) {
				return true;
			}
			选择一个未尝试的赋值{x = 1} 或者{x = 0};
			添加该赋值到 assign;
		}
	}
}

优化 4.1：新的变量选择方法 VSIDS

• VSIDS=Variable State Independent Decaying Sum
• 首先按变量出现次数给所有变量打分
• 添加新子句的时候给子句中的变量加分
• 每隔一段时间把所有变量的分数除以一个常量

从 SAT 到 SMT

SMT 解法

Eager 方法

将 SMT 问题编码成 SAT 问题。

例：将 EUF 编码成 SAT

$$f(a)=c\wedge f(b)\ne c\wedge a\ne b$$

1. 引入符号替代函数调用：A 替代 $f(a)$，B 替代 $f(b)$

原式变为：

$$A=c\wedge B\ne c\wedge a\ne b$$

同时根据公理添加约束：

$$a=b\to A=B$$

2. 引入布尔变量替代等式：

$$\begin{gathered} P_{A=c}\wedge \mathrm{\neg }{P}_{B=c}\wedge \mathrm{\neg }{P}_{a=b}\text{ \\ Pa=b→PA=B} \end{gathered}$$

编码方式蕴含了第二条公理和对称性

3. 根据自反性添加约束，如 $PA=A$，本例中不需要
4. 同时为传递性添加约束

$$\begin{gathered} P_{A=c}\wedge P_{B=c}\to P_{A=B}\text{ \\ PA=B∧PB=c→PA=c \\ PA=B∧PA=c→PB=c \\ } \end{gathered}$$

Eager 算法存在的问题：

1. 很多理论存在专门的求解算法，如
   1. EUF 可以用一个不动点算法不断合并等价类求解
   2. 线性方程组存在专门算法求解
2. 编码成 SAT 之后， SAT 求解器无法利用这些算法
3. 模块化程度不高：
   1. 每种理论都要设计单独的编码方法
   2. 不同理论混合使用时要保证编码方法兼容

Lazy 方法

黑盒混合 SAT 求解器和各种理论求解器

理论求解器：

• 输入：属于特定理论的公式组，组内公式属于合取关系
  • EUF 公式组：
    • $f(a)=c$
    • $f(b)=c$
    • $a\ne b$
  • 线性方程组：
    • $a+b=10$
    • $a-b=4$
• 输出：SAT 或者 UNSAT

DPLL(T) 算法

打破 SAT 黑盒，以 CDCL 算法为中心集成理论求解器