$$ \def\P{\mathcal{P}} \def\V{\mathbb{V}} \def\Tr{\mathbb{Tr}} \def\X{\mathsf{X}} \def\begin{\mathsf{begin}} \def\ld{\mathsf{ld}} \def\isu{\mathsf{isu}} \def\del{\mathsf{del}} \def\end{\mathsf{end}} \def\HB{\mathsf{HB}} \def\CC{\mathtt{CC}} \def\CM{\mathtt{CM}} \def\CCv{\mathtt{CCv}} $$
摘要
分布式存储系统和数据库被各种类型的应用程序广泛使用。对这些存储系统的事务访问是一种重要的抽象,它允许应用程序程序员将操作块(即事务)视为原子执行。出于性能原因,现代数据库实现的一致性模型比标准可序列化模型弱,后者对应于在顺序一致内存上执行的事务的原子性抽象。例如,因果一致性就是在实践中广泛使用的此类模型之一。
在本文中,我们研究了因果一致性的几种变体之间的特定于应用程序的关系,并解决了自动验证给定事务程序是否对因果一致性具有鲁棒性的问题,即在任意因果一致数据库上执行时,其所有行为都是可序列化的。我们表明,没有 ww 竞争的程序在所有这些变化下都具有相同的行为集,并且我们表明,检查鲁棒性是多项式时间可归结为顺序一致共享内存上事务程序的状态可达性问题。后一个结果的一个令人惊讶的推论是,允许不可比较的行为集的因果一致性变体允许可比较的稳健程序集。这种简化还为利用现有的并发程序验证方法和工具(假设顺序一致性)来推理在因果一致的数据库上运行的程序打开了大门。此外,它允许确定当在不同站点执行的程序是有限状态时,检查稳健性的问题是可判定的。
作者:
- Sidi Mohamed Beillahi, Université de Paris, IRIF, CNRS, F-75013 Paris, France
- Ahmed Bouajjani, Université de Paris, IRIF, CNRS, F-75013 Paris, France
- Constantin Enea, Université de Paris, IRIF, CNRS, F-75013 Paris, France
Introduction
广泛采用分布和复制来实现提供高性能和可用服务的存储系统和数据库。这些系统的实现必须确保一致性保证,从而能够以抽象和简单的方式推理其行为。理想情况下,使用此类系统的应用程序程序员希望具有强一致性保证,即系统中任何地方发生的所有更新都能立即被所有站点看到并以相同的顺序执行。此外,应用程序程序员还需要一种抽象机制(如事务),以确保站点的操作块(写入和读取)可以被视为原子执行,而不会受到其他站点操作的干扰。对于事务程序,提供强一致性的一致性模型是可序列化 [37],即程序的每次计算都等同于另一个程序,其中事务一个接一个地串行执行而不会受到干扰。在非事务情况下,此模型对应于顺序一致性(SC)[31]。然而,虽然可序列化和 SC 更容易被应用程序程序员理解,但它们的实施(由存储系统实现者实施)需要在所有站点之间使用全局同步,这很难在确保可用性和可接受的性能的同时实现 [24, 25]。因此,现代存储系统确保的一致性保证较弱。在本文中,我们感兴趣的是研究因果一致性 [30]。
因果一致性是一种基本一致性模型,已在多个生产数据库中实现,例如 AntidoteDB、CockroachDB 和 MongoDB,并在文献中进行了广泛研究 [7、23、33、34、39]。基本上,当在动作层面上定义时,它保证每两个因果相关的动作(比如 𝑎1 在 𝑎2 之前有因果关系(即它对 𝑎2 有影响))都以相同的顺序执行,即 𝑎1 在 𝑎2 之前,所有站点都执行。不同站点可见的更新集可能不同,读取操作可能返回在 SC 执行中无法获得的值。因果一致性的定义可以提升到事务的级别,假设事务对站点来说是完整的可见的(即,它们的所有更新都同时可见),并且它们由站点独立执行,不受其他事务的干扰。与可串行化相比,因果一致性允许冲突事务(即读取或写入公共位置的事务)由不同站点以不同的顺序执行,只要它们没有因果关系。实际上,我们考虑了文献中引入的三种因果一致性变体,即弱因果一致性($\CC$)[38, 14]、因果记忆($\CM$)[3, 38] 和因果收敛($\CCv$)[18]。

因果一致性的最弱变体,即 $\CC$,允许推测执行和回滚无因果关系(并发)的事务。例如,图 1c 中的计算仅在 $\CC$ 下可行:右侧的站点在执行 t3 之前在 t1 之后应用 t2,并在执行 t4 之前回滚 t2。$\CCv$ 和 $\CM$ 提供更多保证。$\CCv$ 在所有事务之间强制执行总仲裁顺序,该顺序定义了每个站点执行已交付并发事务的顺序。这保证了所有事务交付后,所有站点都达到相同的状态。$\CM$ 确保站点读取的所有值都可以通过与因果顺序一致的事务交错来解释,从而在 $\CC$ 之上强制执行 PRAM 一致性 [32]。与 $\CCv$ 相反,$\CM$ 允许两个站点在并发事务的顺序上存在分歧,但两种模型都不允许并发事务的回滚。因此,$\CCv$ 和 $\CM$ 在它们允许的计算方面是无法比较的。图 1a 中的计算不被 $\CM$ 接受,因为这些事务之间没有交错,无法解释右侧站点读取的值:从 z 读取 0 意味着左侧的事务必须在 t3 之后应用,而从 y 读取 1 意味着 t1 和 t2 都在 t4 之前应用,这与从 x 读取 2 相矛盾。但是,这种计算在 $\CCv$ 下是可能的,因为 t1 可以在执行 t3 之后传递到右侧,但在 t3 之前进行仲裁,这意味着 t1 中对 x 的写入将丢失。图 1b 中的 $\CM$ 计算在 $\CCv$ 下是不可能的,因为没有仲裁顺序可以解释从 x 进行的两次读取。
作为本文的第一项贡献,我们表明,对于不包含写入-写入竞争的事务程序(即并发事务写入公共变量),三种因果一致性语义是一致的。我们还表明,如果事务程序在其中一个语义下存在写入-写入竞争,那么它在其他两种语义中的任何一种下也必须存在写入-写入竞争。此属性相当违反直觉,因为 $\CC$ 严格弱于 $\CCv$ 和 $\CM$,并且 $\CCv$ 和 $\CM$ 无法比较(就承认的行为而言)。请注意,图 1b、1a 和 1c 中的每个计算都包含写入-写入竞争,这解释了为什么这三种语义下都不可能进行这些计算。
然后,我们研究检查应用程序对因果一致性放松的稳健性的问题:给定一个程序 $P$ 和一个因果一致性变体 $X$,如果 $P$ 在 $X$ 下运行时的计算集与在可序列化下运行时的计算集相同,则我们说 $P$ 对 $X$ 具有稳健性。这意味着可以推断 $P$ 的行为,假设更简单的可序列化模型,并且当 $P$ 在 $X$ 下运行时不需要额外的同步,以便它保持在可序列化下满足的所有属性。检查稳健性并不简单,它可以看作是检查程序等价性的一种形式。然而,要检查的等价性是在同一程序的两个版本之间,使用两种不同的语义获得,一个比另一个更宽松。目标是检查这种宽松性实际上对所考虑的特定程序没有影响。检查鲁棒性的难点在于理解由于放宽一致性模型相对于可序列化性引入的重新排序而产生的额外行为。这需要对任意长计算中的操作之间的复杂顺序约束进行先验推理,这可能需要维护无界有序结构,并使检查鲁棒性的问题变得困难甚至无法判定。
我们证明了,验证事务程序对因果一致性的鲁棒性可以在多项式时间内简化为 SC 上并发程序的可达性问题。这允许使用现有的验证技术来推理在因果一致性存储系统上运行的分布式应用程序,并且它意味着鲁棒性问题对于有限状态程序是可判定的;当站点数量固定时,问题是 PSPACE-完全的,否则是 EXPSPACE-完全的。这是关于验证因果一致性鲁棒性的可判定性和复杂性的第一个结果。事实上,文献中已经考虑了几种分布式系统一致性模型的鲁棒性验证问题,包括因果一致性 [12, 16, 17, 20, 35]。这些工作提供了检查鲁棒性的(过度或不足)近似分析,但它们都没有提供解决该问题的精确(合理和完整)算法验证方法,也没有解决其可判定性和复杂性。
我们采用的解决此验证问题的方法是基于对稳健性违规集的精确描述,即因果一致但不可序列化的执行。对于 $\CCv$ 和 $\CM$,我们表明搜索一种特殊类型的稳健性违规就足够了,这种违规可以通过对原始程序的仪表进行串行(SC)计算来模拟。这些计算保留了识别因果一致语义(执行同一组操作)下原始程序中可能发生的违规模式所需的信息。这些结果的一个令人惊讶的结果是,当且仅当程序对 $\CC$ 具有稳健性时,它才对 $\CM$ 具有稳健性,并且对 $\CM$ 的稳健性意味着对 $\CCv$ 具有稳健性。这表明,我们研究的因果一致性变化在承认的行为方面无法比较,但在它们支持的稳健应用程序方面可以比较。
Causal Consistency
Program syntax
我们考虑一个简单的编程语言,其中一个程序 $\P$ 是进程的并行组合,这些进程通过一组标识符 $\mathbb{P}$ 区分开来。每个进程是事务的序列,而每个事务是标记指令的序列。每个事务以 begin 指令开始,并以 end 指令结束。其他指令要么是对进程本地寄存器(来自寄存器集 $\R$)的赋值,要么是对共享变量(来自变量集 $\V$)的赋值,或者是 assume 语句。赋值使用的数据来自数据域 $\D$。对寄存器的赋值 $\langle reg \rangle := \langle var \rangle$ 称为读取 $\langle var \rangle$,而对共享变量的赋值 $\langle var \rangle := \langle \textit{reg-expr} \rangle$ 称为写入 $\langle var \rangle$($\langle \textit{reg-expr} \rangle$ 是一个基于寄存器的表达式)。assume 语句在布尔表达式 $\langle \textit{bexpr} \rangle$ 结果为 false 时阻塞进程。每个指令后跟一个 goto 语句,用来定义程序计数器的变化。多个指令可以关联到相同的标签,这允许我们编写非确定性的程序,而多个 goto 语句可以将控制流指向相同的标签,从而模拟循环和条件语句等命令式结构。我们假设控制流不会在事务之间跳转,必须通过 begin 和 end 指令来标记事务的开始和结束。
Causal memory (CM) semantics
在因果内存下,程序的语义定义如下。共享变量被复制到每个进程中,每个进程维护自己对这些变量的本地值。在进程中执行事务期间,对共享变量的写操作存储在事务日志中,该日志仅对执行该事务的进程可见,并在事务结束时广播给所有其他进程。要读取共享变量 $x$,进程 $p$ 首先访问其事务日志,并获取 $x$ 的最后写入值(如果存在),然后从本地存储中读取 $x$ 的值(如果在当前事务中没有写入 $x$)。事务日志按照与事务之间的因果传递关系一致的顺序传递,即程序顺序(进程执行事务的顺序)和传递之前关系的并集的传递闭包(即,如果事务 $t_1$ 的日志在 $t_1$ 开始之前已经被传递给执行 $t_2$ 的进程,则称 $t_1$ 被传递在 $t_2$ 之前)。这种性质称为“因果传递”。一旦事务日志被传递,它将立即应用于接收进程的共享变量值。此外,当进程 $p$ 正在执行另一个事务时,事务日志不能传递给该进程。我们称这一性质为“事务隔离”。
Causal convergence (CCv) semantics
与因果内存相比,因果收敛确保进程本地的共享变量副本最终一致。每个事务日志与一个时间戳关联,进程仅在时间戳大于它已应用的所有事务日志(且写入相同变量 $x$ 的日志)的时间戳时,才会应用事务日志中的写操作。为简化起见,我们假设事务标识符充当时间戳,并且它们根据某种关系 $<$ 完全有序。CCv 满足因果传递和事务隔离。
Weak causal consistency (CC) semantics
相比前述语义,CC 允许同一进程的读取操作观察到并发写操作的不同执行顺序。每个进程为每个共享变量维护一个值集合,读取操作可以从中任意返回一个值。事务日志与向量时钟关联,向量时钟表示因果传递关系。即,如果事务 $t_1$ 的向量时钟小于事务 $t_2$ 的向量时钟,则事务 $t_1$ 在因果传递上先于 $t_2$。我们假设事务标识符充当向量时钟,并且它们根据某种部分有序关系 $<$ 排序。当将事务日志应用于接收进程的共享变量时,仅保留由并发事务写入的值(与因果传递无关的事务写入值)。CC 满足因果传递和事务隔离。
Program execution

在因果一致性语义 $\X \in \set{\CCv, \CM, \CC}$ 下,程序 $\P$ 的语义通过标记转换系统 $[\P]_\X$ 来定义,转换标签(称为事件)的集合 $\Ev$ 定义如下:
$$ \Ev = \set{\begin(p, t), \ld(p, t, x, v), \isu(p, t, x, v), \del(p, t), \end(p, t) \mid p \in \mathbb{P}, t \in \T, x \in \V, v \in \D } $$
其中,begin 和 end 标记事务的开始和结束,isu 和 ld 标记事务期间的写入和读取共享变量的操作,del 标记从其他进程接收到的事务日志在本地共享变量副本上的应用。事件 isu 称为“发出”,而事件 del 称为“存储”。$[\P]_\X$ 的执行是事件序列 $\rho = \mathtt{ev}_1 \cdot \mathtt{ev}_2 \cdot \dots$,其中的每个事件为转换标签。图 2a 显示了在 CM 下的一个执行。这种执行在 CCv 下是不可能的,因为 $t_4$ 和 $t_2$ 分别从 $x$ 中读取了 2 和 1。这只有在 $t_1$ 和 $t_3$ 分别在 $p_2$ 和 $p_1$ 写入 $x$ 时才有可能发生,这与 CCv 的定义相矛盾,因为在 CCv 中不可能同时有 $t_1 < t_3$ 和 $t_3 < t_1$。
图 2b 显示了在 CCv 下的一个执行(我们假设 $t_1 < t_2 < t_3 < t_4$)。请注意,del(p_2, t_1) 并没有导致 $x$ 的更新,因为时间戳 $t_1$ 小于 $p_2$ 最后一次写入 $x$ 的事务(即 $t_3$)的时间戳,这种行为在 CM 下是不可能的。两个进程在执行结束时达成一致,并存储了相同的共享变量副本。
图 2c 显示了在 CC 下的一个执行,这在 CCv 和 CM 下是不可能的,因为 $t_3$ 和 $t_4$ 分别读取了 2 和 1。由于 $t_1$ 和 $t_2$ 是并发的,$p_2$ 存储了由这些事务写入的值 2 和 1。读取 $x$ 时可以返回其中的任意一个值。
Execution summary
令 $\rho$ 是在 $\X \in \set{\CCv, \CM, \CC}$ 下的一个执行,一个事件序列 $\tau$ 是 $\rho$ 的摘要,如果它通过将 $\rho$ 中的每个由 begin 和 end 限定的转换子序列替换为单个“宏事件” $\isu(p, t)$ 来获得。例如,$\isu(p_1, t_1) \cdot \isu(p_2, t_3) \cdot \del(p_1, t_3) \cdot \del(p_2, t_1) \cdot \isu(p_2, t_4) \cdot \isu(p_1, t_2)$ 是图 2a 中执行的摘要。
我们说,在 $\rho$ 中,事务 $t$ 对变量 $x$ 执行了外部读取,如果 $\rho$ 包含事件 ld(p, t, x, v),并且在 $t$ 之前没有对 $x$ 的写入操作(即 $\isu(p, t, x, v)$)。在 CM 和 CC 下,如果 $\rho$ 包含 $\isu(p, t, x, v)$,则事务 $t$ 对 $x$ 进行了写入。在图 2a 中,$t_2$ 和 $t_4$ 执行了外部读取,而 $t_2$ 对 $y$ 进行了写入。进程 $p$ 执行的事务 $t$ 对另一个进程 $p' \neq p$ 写入 $x$,如果 $t$ 对 $x$ 进行了写入,并且 $\rho$ 包含事件 $\del(p', t)$(例如,在图 2a 中,$t_1$ 对 $p_2$ 写入了 $x$)。在 CCv 下,我们说进程 $p$ 执行的事务 $t$ 对进程 $p' \neq p$ 写入了 $x$,如果 $t$ 对 $x$ 进行了写入,并且 $\rho$ 包含事件 $\del(p', t)$,该事件没有被另一个事务 $t'$ 之前的事件 $\del(p', t')$(或 $\isu(p', t')$)所取代,且 $t < t'$ 并且 $t'$ 对 $x$ 进行了写入(如果有这样的事件在之前,那么 $t$ 对 $x$ 的写入将被丢弃)。例如,在图 2b 中,$t_1$ 并没有对 $p_2$ 写入 $x$。
Write-Write Race Freedom
Programs Robustness
Program Traces
我们定义了一个满足事务隔离的执行抽象,称为轨迹。直观上,轨迹忽略了事务内部访问共享变量的顺序以及访问不同变量的事务之间的顺序。执行 $\rho$ 的轨迹是通过在其摘要中添加若干标准关系来记录数据流(例如,一个事务读取的值是由哪个事务写入的)。 轨迹的事件序列由以下事件构成: $$ Ev = \set{\mathtt{begin}(p, t), \mathtt{ld}(p, t, x, v), \isu(p, t, x, v), \del(p, t), \mathtt{end}(p, t) \mid p \in P, t \in T, x \in V, v \in D } $$ 其中 $\mathtt{begin}(p, t)$ 和 $\mathtt{end}(p, t)$ 分别表示事务的开始和结束,$\mathtt{ld}(p, t, x, v)$ 表示读取事件,$\isu(p, t, x, v)$ 表示写入事件,$\del(p, t)$ 表示从其他进程接收到的事务日志。轨迹通过保持事务隔离来记录事件顺序。
Program Semantics Under Serializability
在因果一致性模型下,程序的轨迹包含根据 $\mathsf{HB}$ (先行关系)的事务顺序。我们关注满足 $\mathsf{HB}$ 顺序的轨迹,这些轨迹中的每个事务都符合事务隔离原则。不同一致性模型允许不同的轨迹,例如,串行化模型下的轨迹与因果一致性模型下的轨迹可能有所不同。
Robustness Problem
我们考虑检查程序在因果一致性语义下是否产生与串行化语义相同的 trace 集的问题。
定义 4
给定一个程序 $\P$ 和语义 $X \in \set{\CCv, \CM, \CC}$,如果 $\Tr_X(\P) = \Tr_{\SER}(\P)$,则称程序 $\P$ 对 $X$ 具有鲁棒性。
由于 $\Tr_{\SER}(\P) \subseteq \Tr_X(\P)$,因此检查程序 $\P$ 在语义 $X$ 下的鲁棒性问题可归结为检查是否存在路径 $tr \in \Tr_X(\P) \setminus \Tr_{\SER}(\P)$。我们称 $tr$ 为鲁棒性违例(或简称为违例)。根据定理 3,$tr$ 的事务先行关系 $\HB_t$ 是有环的。

我们讨论一些程序在 $\CM$ 和 $\CCv$ 下(非)鲁棒的例子,或仅在其中一个语义下非鲁棒。图 4a 和图 4b 展示了在 $\CM$ 和 $\CCv$ 下都不具有鲁棒性的程序例子,这些例子也在关于弱内存模型的文献中讨论过,例如 [6]。在 $\CM$ 和 $\CCv$ 下执行 Lost Update 程序允许两个事务 $t_1$ 和 $t_2$ 对 $x$ 的读取都返回 0,尽管在串行化语义下不可能发生这种情况。此外,执行 Store Buffering 程序允许对 $x$ 和 $y$ 的读取都返回 0,尽管在串行化语义下也不可能发生这种情况。这些值是可能的,因为每个进程的第一个事务可能不会传递给另一个进程。
假设图 4c 和图 4d 中的每个指令都形成一个不同的事务,那么我们在注释中给出的值表明,图 4c 的程序分别在 $\CCv$ 下非鲁棒,图 4d 的程序在 $\CM$ 下非鲁棒。图 4c 中的值在 $\CCv$ 下是可能的,假设事务 $[x = 1]$ 的时间戳比 $[x = 2]$ 的时间戳小(这意味着如果前者在第二个进程执行 $[x = 2]$ 之后传递,则它将被丢弃)。此外,将事务扩展如图 4c 所示,程序对 $\CCv$ 是鲁棒的。图 4d 中的值在 $\CM$ 下是可能的,因为不同的进程不需要就应用事务的顺序达成一致,每个进程都将最后接收到的事务应用。然而,在 $\CCv$ 下这种行为是不可能的,程序实际上对 $\CCv$ 是鲁棒的。如前所述,将事务扩展如图所示会使程序对 $\CM$ 是鲁棒的。
最后,我们展示了一些对 $\CM$ 和 $\CCv$ 都鲁棒的程序例子。这些是简化的模型,源自 [28] 中报告的真实应用。图 4e 中的程序可以理解为两个进程的并行执行:它们要么创建一个新的服务用户(抽象表示为对变量 $x$ 的写操作),要么检查其凭证(抽象为对 $x$ 的读取,非确定性选择抽象了某些代码来检查用户是否存在)。显然,该程序对 $\CM$ 和 $\CCv$ 都是鲁棒的,因为每个进程只对共享变量进行了单次访问。尽管我们考虑了简单的事务(仅访问一个共享变量),这一结论也适用于访问任意数量变量的“更大”事务。图 4f 中的程序可以被理解为一个进程创建一个新用户并读取一些附加数据,另一个进程并行地更新该数据,前提是用户存在。很容易看出,该程序对 $\CM$ 和 $\CCv$ 都是鲁棒的。
Robustness Against Causal Consistency
接下来我们讨论在因果一致性变体下检查程序鲁棒性的问题,首先考虑 $\CCv$ 和 $\CM$ 的情况。对于 $\CC$ 的结果是由 $\CM$ 的结果推导出来的。接下来我们证明,鲁棒性违例中,必须包含同一事务的发出和存储事件,并且这两个事件之间必须由发生在发出之后、存储之前的另一个事件隔开,且该事件通过先行关系与两者相关联。否则,由于两个没有先行关系的事件可以交换顺序来推导出相同的 trace,因此每个存储事件可以被交换,直到它紧随其发出事件,从而使得执行是可串行化的。
引理 5
给定一个鲁棒性违例 $\tau$,存在某个事务 $t$ 使得 $\tau = \alpha \cdot \isu(p, t) \cdot \beta \cdot \del(p', t) \cdot \gamma$,并且存在事件 $a \in \beta$,满足 $(\isu(p, t), a) \in \HB$ 且 $(a, \del(p', t)) \in \HB$。
上面 trace 中的事务 $t$ 被称为延迟事务。先行关系的约束表明 $t$ 属于 $\HB_t$ 循环。
接下来我们展示,程序在 $\CCv$ 或 $\CM$ 下不鲁棒,当且仅当它允许违例形状的 trace,这使得鲁棒性检查问题可以归约为程序在串行化语义下的可达性问题(详见第 6 节)。
Robustness Violations under Causal Convergence
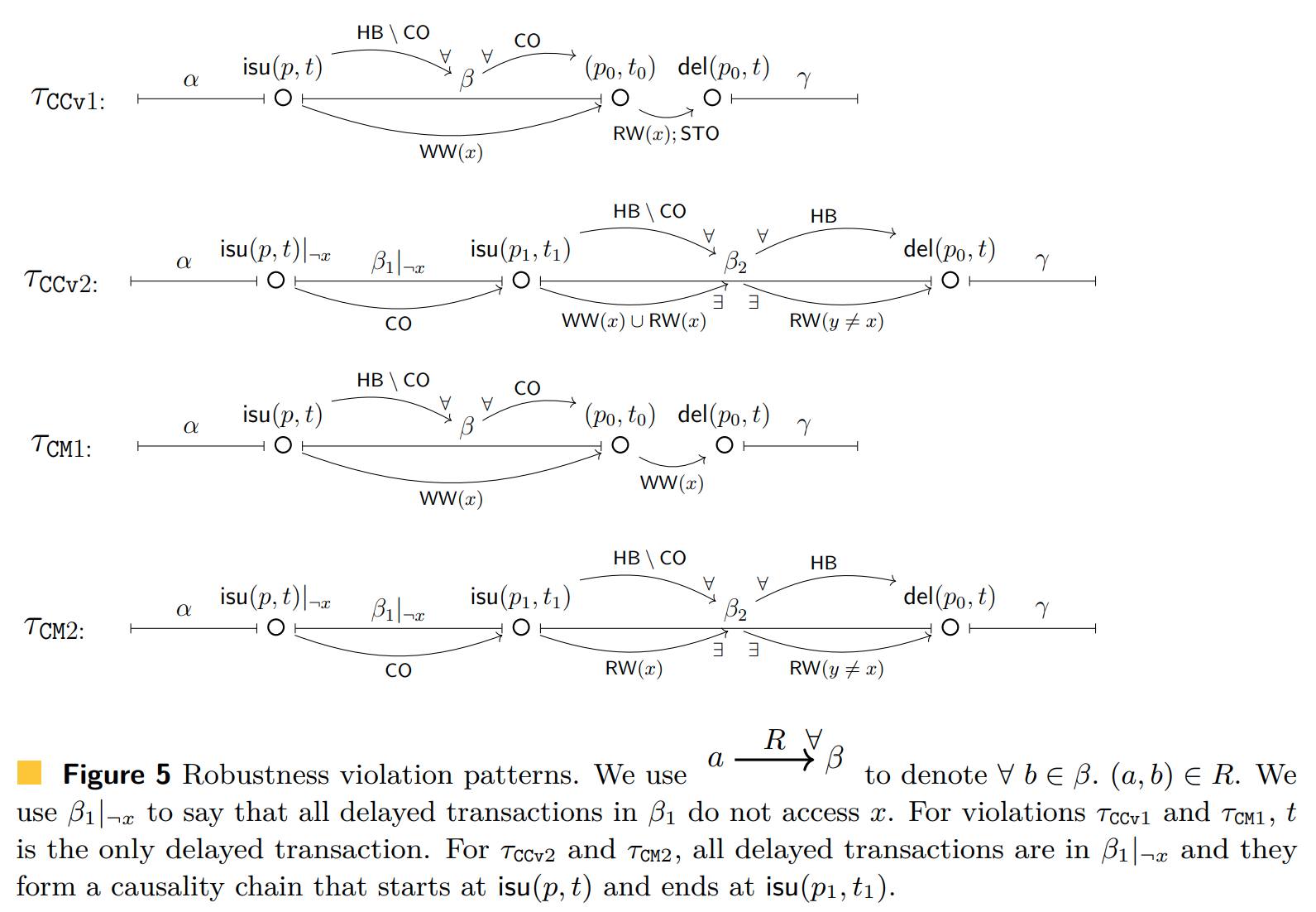
简而言之,我们对 $\CCv$ 鲁棒性违例的刻画表明,第一个延迟事务(根据引理 5 必然存在)后跟一个可能为空的延迟事务序列,这些延迟事务形成一个“因果链”,即每个新的延迟事务在因果顺序上跟随前一个延迟事务。此外,最后一个延迟事务的发出事件发生在另一个事务的发出事件之前,且该事务读取了第一个延迟事务更新的变量(这完成了 $\HB_t$ 中的一个循环)。我们称发出事件序列 $\mathsf{ev}_1 \cdot \mathsf{ev}_2 \cdot \dots \mathsf{ev}_n$ 形成因果链,当且仅当对于所有 $1 \leq i \leq n-1$,$(\mathsf{ev}i, \mathsf{ev}{i+1}) \in \CO$。为简单起见,我们在因果一致性下得到的 trace 中也使用“宏事件”(即 $(p, t)$),这最初用于简化可串行化的 trace。
定理 6 $\CCv$ 下鲁棒性充要条件
如果程序 $\P$ 在 $\CCv$ 下不鲁棒,当且仅当 $\Tr(\P){\CCv}$ 包含形如 $\tau{\CCv1} = \alpha \cdot \isu(p, t) \cdot \beta \cdot (p', t') \cdot \del(p', t) \cdot \gamma$ 或 $\tau_{\CCv2} = \alpha \cdot \isu(p, t) \cdot \beta_1 \cdot \isu(p_1, t_1) \cdot \beta_2 \cdot \del(p', t) \cdot \gamma$ 的 trace,且满足图 5 中给出的性质。
在 $\tau_{\CCv1}$ 中包含一个延迟事务,而 $\tau_{\CCv2}$ 可以包含任意多个延迟事务。最后一个延迟事务的发出事件(即 $\tau_{\CCv1}$ 中的 $\isu(p, t)$ 或 $\tau_{\CCv2}$ 中的 $\isu(p_1, t_1)$)分别发生在 $(p', t')$ 和 $\beta_2$ 中的某个事件之前,这些事件读取了由第一个延迟事务更新的变量。定理允许 $\beta_1 = \epsilon, \beta_2 = \epsilon, \beta = \epsilon, \gamma = \epsilon, p = p_1, t = t_1$,且 $t_1$ 可以是只读事务。如果 $t_1$ 是只读事务,那么 $\isu(p_1, t_1)$ 的效果与 $(p_1, t_1)$ 相同,因为 $t_1$ 不包含写操作。图 6a 和图 6b 展示了 $\CCv$ 下的两个违例。
定理 6 中的违例模式刻画了最小的鲁棒性违例,其中度量定义为同一事务发出和存储事件之间的距离(与发出相关的事件数量)的总和是最小的。最小性保证了上面描述的约束。
Robustness Violations under Causal Memory
$\CM$ 下的鲁棒性违例与 $\CCv$ 下的鲁棒性违例有某种程度上的相似性。然而,$\CCv$ 下的一些违例模式在 $\CM$ 下是不可行的,而 $\CM$ 允许的某些违例模式在 $\CCv$ 下也是不可能的。这反映了这两种一致性模型在一般情况下是不可比的。以下定理给出了精确的刻画。简单来说,程序不鲁棒是因为它允许违例,这可能是由于两个并发的事务写入相同的变量(写-写竞争),或者由于 $\CCv$ 模式的某个限制,其中最后一个延迟事务必须仅通过 $\RW$ 与未来的事务在先行路径上相关联。第一个模式在 $\CCv$ 下是不允许的,因为对每个变量的写入是按照时间戳顺序执行的。
定理 7 $\CM$ 下鲁棒性充要条件
如果程序 $\P$ 在 $\CM$ 下不鲁棒,当且仅当 $\Tr(\P){\CM}$ 包含形如 $\tau{\CM1} = \alpha \cdot \isu(p, t) \cdot \beta \cdot (p', t') \cdot \del(p', t) \cdot \gamma$ 或 $\tau_{\CM2} = \alpha \cdot \isu(p, t) \cdot \beta_1 \cdot \isu(p_1, t_1) \cdot \beta_2 \cdot \del(p', t) \cdot \gamma$ 的 trace,且满足图 5 中给出的性质。
图 6b 中的 $\CM$ 违例(模式 $\tau_{\CM2}$)也是 $\CCv$ 下的违例,模式对应于 $\tau_{\CCv2}$。检测违例模式 $\tau_{\CM1}$(例如,图 6c)意味着在 $\CM$ 下存在写-写竞争。反之,如果程序存在包含写-写竞争的 trace,那么该 trace 必然是鲁棒性违例,因为引起写-写竞争的两个事务在存储顺序上形成了一个循环,因此在事务先行关系上也形成了一个循环。因此,程序在 $\CM$ 下不鲁棒。因此,程序在 $\CM$ 下鲁棒也意味着它在 $\CM$ 下不存在写-写竞争。由于没有写-写竞争,$\CM$ 和 $\CCv$ 语义一致,我们得到以下结论。
引理 8
若程序 $\P$ 对 $\CM$ 鲁棒,则其对 $\CCv$ 鲁棒。
Robustness Violations under Weak Causal Consistency
如果程序对 $\CM$ 是鲁棒的,那么它在 $\CM$ 下不存在写-写竞争(注意,这对 $\CCv$ 并不成立)。因此,根据定理 2,一个对 $\CM$ 鲁棒的程序在 $\CM$ 和 $\CC$ 下具有相同的 trace 集,这意味着它对 $\CC$ 也是鲁棒的。反之,由于 $\CC$ 弱于 $\CM$(即 $\Tr_{\CM}(\P) \subseteq \Tr_{\CC}(\P)$),如果程序对 $\CC$ 是鲁棒的,那么它对 $\CM$ 也是鲁棒的。因此,我们得到以下结论。
定理 9 $\CC$ 下鲁棒性充要条件
程序 $\P$ 对 $\CC$ 鲁棒,当且仅当其对 $\CM$ 鲁棒。
Reduction to SC Reachability
Related Work
因果一致性是分布式系统最古老的一致性模型之一 [30]。最近,人们引入了几种适用于不同类型应用的因果一致性变体的正式定义 [19, 18, 38, 14]。本文中的定义受到这些工作的启发,与 [14] 中的定义一致。在那篇论文中,作者讨论了可判定性和验证存储系统实现是否具有因果一致性(即,对于每个客户端,其所有计算都是因果一致的)的复杂性。
虽然我们的论文重点关注基于跟踪的鲁棒性,但基于状态的鲁棒性要求程序在弱语义下所有可达状态的集合与强语义下的可达状态集相同时,才是鲁棒的。虽然状态鲁棒性是保持状态不变量的必要和充分概念,但其验证(即计算弱语义下的可达状态集)通常是一个难题。已经在 TSO 和 Power 等宽松记忆模型的背景下研究了该问题的可判定性和复杂性,结果表明它要么是可判定的但非常复杂(非原始递归),要么是不可判定的 [8, 9]。据我们所知,尚未针对因果一致性研究该问题的可判定性和复杂性。已经提出了使用抽象或有界分析来自动检查近似可达性/不变量的程序,例如 [10, 5, 21, 1]。人们也开发了用于验证弱一致性模型中不变量的证明方法,如 [29, 26, 36, 4]。然而,这些方法不提供决策程序。
针对 TSO 和 Power 内存模型,已经研究了基于轨迹的鲁棒性的可判定性和复杂性 [15, 13, 22]。我们在本文中介绍的工作借鉴了使用最小违规表征来构建仪器的想法,从而可以将鲁棒性检查问题简化为 SC 上的可达性检查问题。但是,将这种方法应用于因果一致性的情况并不简单,需要不同的证明技术。处理因果一致性比处理 TSO 更加棘手和困难,并且需要提出完全不同的论据和证明,以便(1)以有限的方式表征违规集,(2)证明这种表征是合理和完整的,以及(3)在可达性问题简化的定义中有效地使用这种表征。
据我们所知,我们的工作是第一个在因果一致性的背景下,考虑到事务的情况下,对鲁棒性问题的可判定性和复杂性问题建立结果的工作。现有的分布式系统鲁棒性验证工作主要考虑基于跟踪的鲁棒性概念,并提供过度或欠近似的分析来检查它。[12、16、17、20] 中提出的静态分析基于计算一组计算的抽象,该抽象用于搜索鲁棒性违规。这些方法可能会由于它们考虑的抽象而返回错误警报。特别是,[12] 表明,当且仅当因果收敛下的跟踪包含具有 RW 依赖项和另一个 RW 或 WW 依赖项的(事务性)发生前循环时,它才不被可序列化语义所接受。仅凭这种表征不足以证明定理 10 中的简化,这需要更精细地表征鲁棒性违规。 [35] 提出了一种用于检测鲁棒性违规的合理(但不完整)有界分析。我们的方法在技术上有所不同,非常精确,并且提供了在程序为有限状态时检查鲁棒性的决策程序。

