$$ \def\po{\mathsf{\textcolor{red}{po}}} \def\AR{\mathsf{\textcolor{brown}{AR}}} \def\VIS{\mathsf{\textcolor{orange}{VIS}}} \def\Obj{\mathsf{Obj}} \def\Op{\mathsf{Op}} \def\Hist{\mathsf{Hist}} \def\Event{\mathsf{Event}} \def\REvent{\mathsf{REvent}} \def\WEvent{\mathsf{WEvent}} \def\HEvent{\mathsf{HEvent}} \def\EventId{\mathsf{EventId}} \def\read{\mathtt{read}} \def\write{\mathtt{write}} \def\H{\mathcal{H}} \def\A{\mathcal{A}} $$
摘要
现代分布式系统通常依赖于数据库,这些数据库通过仅提供关于分布式事务处理一致性的弱保证来实现可扩展性。与此类数据库交互的程序的语义取决于其一致性模型,该模型定义了这些保证。不幸的是,一致性模型通常是非正式的或使用不同的形式主义,通常与数据库内部相关。为了解决这个问题,我们提出了一个框架,用于统一和声明性地指定各种事务一致性模型。
我们的规范以弱内存模型的形式给出,使用事件和关系结构。这些规范特别简洁,因为它们利用了许多一致性模型保证的原子可见性属性:事务的所有更新或所有更新都对另一个事务可见。这允许规范从事务内部的单个事件中抽象出来。我们通过指定几个现有的一致性模型来说明我们框架的使用。为了验证我们的规范,我们证明它们等同于替代操作规范,这些规范是更接近实际实现的算法。我们的工作为开发弱一致性大规模数据库中出现的新形式并发的元理论提供了严格的基础。
作者:
- Andrea Cerone, IMDEA Software Institute
- Giovanni Bernardi, IMDEA Software Institute
- Alexey Gotsman, IMDEA Software Institute
Introduction
Abstract Executions
我们考虑一个存储对象 $\Obj = \set{x, y, \ldots}$ 的数据库,为了简化,我们假设这些对象是整数值的。客户端通过在对象上发出 $\read$ 和 $\write$ 操作与数据库交互,这些操作被分组为事务。我们令 $\Op = \set{\read(x, n), \write(x, n) \mid x \in \Obj, n \in \mathbb{Z}}$ 描述可能的操作调用:从对象 $x$ 读取值 $n$ 或者向 $x$ 写入 $n$。
为了指定一个一致性模型,我们需要定义它允许的所有客户端-数据库交互的集合。我们首先引入结构来记录这种交互,在一个单独的数据库计算中,称为历史。在这些历史中,我们使用形式为 $(\iota, o)$ 的历史事件来表示操作调用,其中 $\iota$ 是来自可数无限集合 $\EventId$ 的标识符,而 $o \in \Op$。我们使用 $e, f, g$ 来表示历史事件。我们令 $\WEvent_x = \set{(\iota, \write(x, n)) \mid \iota \in \EventId, n \in \mathbb{Z}}$,类似地定义读事件的集合 $\REvent_x$,并令 $\HEvent_x = \REvent_x \cup \WEvent_x$。如果一个关系是传递的、非自反的,并且以某种方式关联每一对不同的元素,则该关系是一个全序。
定义 1:一个事务 $T, S, \ldots$ 是一对 $(E, \po)$,其中 $E \subseteq \Event$ 是具有不同标识符的有限、非空事件集合,而程序顺序 $\po$ 是 $E$ 上的全序。一个历史 $\H$ 是具有不同事件标识符集合的(有限或无限)事务集合。
历史中的所有事务都假定已提交:为了简化表述,我们的规范不限制在中止或正在进行的事务中读取的值。
为了定义给定一致性模型允许的历史集合,我们引入抽象执行,这些抽象执行通过在事务上添加某些关系来丰富历史,声明性地描述数据库如何处理它们。然后通过限制这些关系来定义一致性模型。如果关系中的每个元素在关系的传递闭包中只有有限多个前驱,则我们称该关系是前缀有限的。
定义 2:一个抽象执行是一个三元组 $\A = (\H, \VIS, \AR)$,其中:
- 可见性(visibility) $\VIS \subseteq \H \times \H$ 是一个前缀有限的、无环的关系;并且
- 仲裁(arbitration) $\AR \subseteq \H \times \H$ 是一个前缀有限的、全序关系,满足 $\AR \supseteq \VIS$。
我们经常写作 $T \xrightarrow{\VIS} S$ 来代替 $(T, S) \in \VIS$,对于 $\AR$ 同理。图 3(a) 给出了一个对应于 $\S 1$ 中解释的异常的执行。非正式地说,$T \xrightarrow{\VIS} S$ 意味着 $S$ 知道 $T$,因此 $T$ 的效果可以影响 $S$ 中操作的结果。在实现方面,如果 $T$ 执行的更新已经被传递到执行 $S$ 的副本,那么可能会出现这种情况;前缀有限性要求确保可能只有有限多个这样的事务 $T$。我们称不通过可见性关联的事务是并发的。关系 $T \xrightarrow{\AR} S$ 意味着 $S$ 写入的对象版本取代了 $T$ 写入的版本;例如,在图 3(a) 中,评论取代了空。约束 $\AR \supseteq \VIS$ 确保事务 $T$ 的写入取代了 $T$ 知道的那些写入;因此 $\AR$ 本质上确保了事务 $T$ 的写入只取代那些 $T$ 知道的事务的写入。在实现中,可以通过给事务分配时间戳来建立仲裁。
一致性模型规范是一组一致性公理 $\Phi$,限制执行。该模型允许那些存在满足公理的执行的历史:
$$ \Hist_\Phi = \set{\H \mid \exists \VIS, \AR. (\H, \VIS, \AR) \models \Phi} $$
我们的一致性公理不限制数据库客户端执行的操作。我们可以通过限制上述集合来获得特定程序与数据库交互产生的历史的集合,如 (1),这在弱内存模型定义中是标准的做法 [7]。
历史 $\H$ 和抽象执行 $\A = (\H, \VIS, \AR)$ 的区别在于:
- $\A$ 的信息量比 $\H$ 更大,一个 $\H$ 可以对应多个 $\A$;
- 本文的公理是用于描述一个满足隔离级别的 $\A$ 应该有哪些约束;
- 我们说 $\H$ 满足某个隔离级别 $\Phi$,当且仅当 $\exists \VIS, \AR. (\H, \VIS, \AR) \models \Phi$。
Adya 体系用于描述执行历史,$(\VIS, \AR)$ 体系用于描述抽象执行。目前没有基于 $(\VIS, \AR)$ 体系的一致性验证算法。
TODO:$\VIS$ 关系如何确定?
Specifying Transactional Consistency Models
事务中有两种偏序,仲裁序 $\AR$ 和可见序 $\VIS$,且 $\VIS \subseteq \AR$。
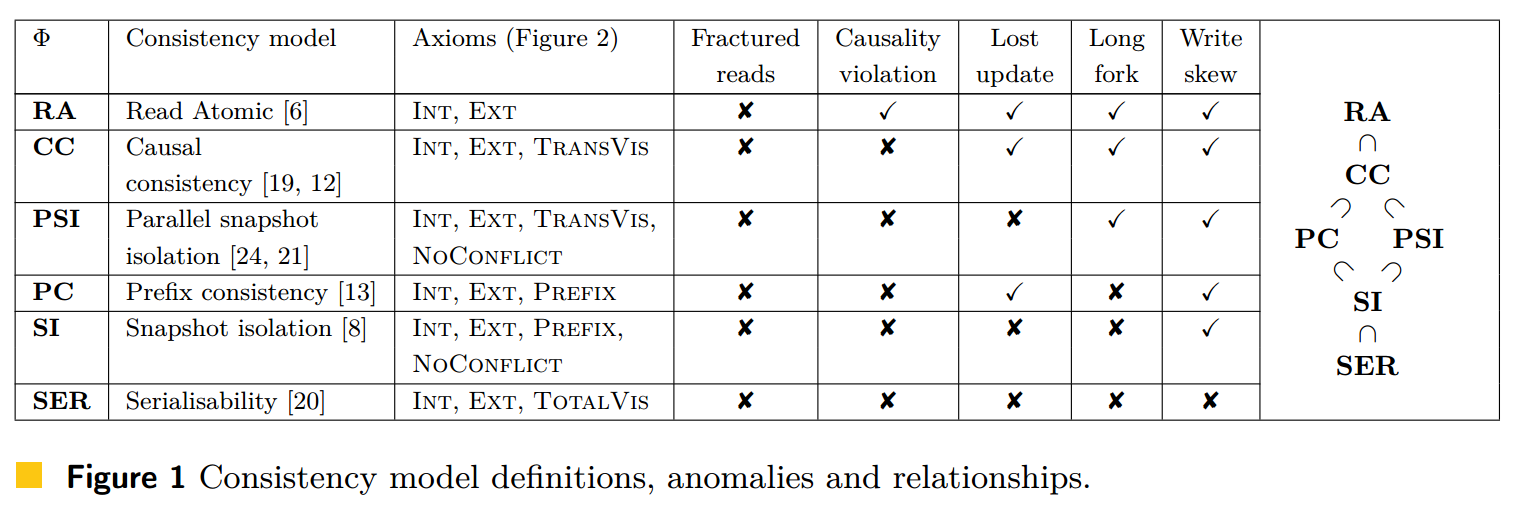
其中:
- Int 是内部一致性公理,对于事务内先写后读,要求所写即所读;
- Ext 是外部一致性公理,对于事务内不写即读,要求读到的是最后一个外部写;
- Int 和 Ext 共同避免不完整的读 Fractured reads,保证了原子读 RA;
- TransVis 是可见性传递公理,要求事务间的可见性关系 VIS 是传递性的,避免了因果违规 Causality violation,保证了 CC;
- NoConflict 公理要求不会对同一个变量并发写入,避免了丢失更新 Lost update,保证了 PSI;
- Prefix 公理要求,如果 T 能观察到 S,则 T 也能观察到 S 的所有 AR-前缀,该公理避免了 Long fork;
- NoConflict 和 Prefix 共同保证了 SI;
- TotalVis 公理要求 VIS 是一个全序,保证了 SER。
公理形式化定义

违反公理的示例
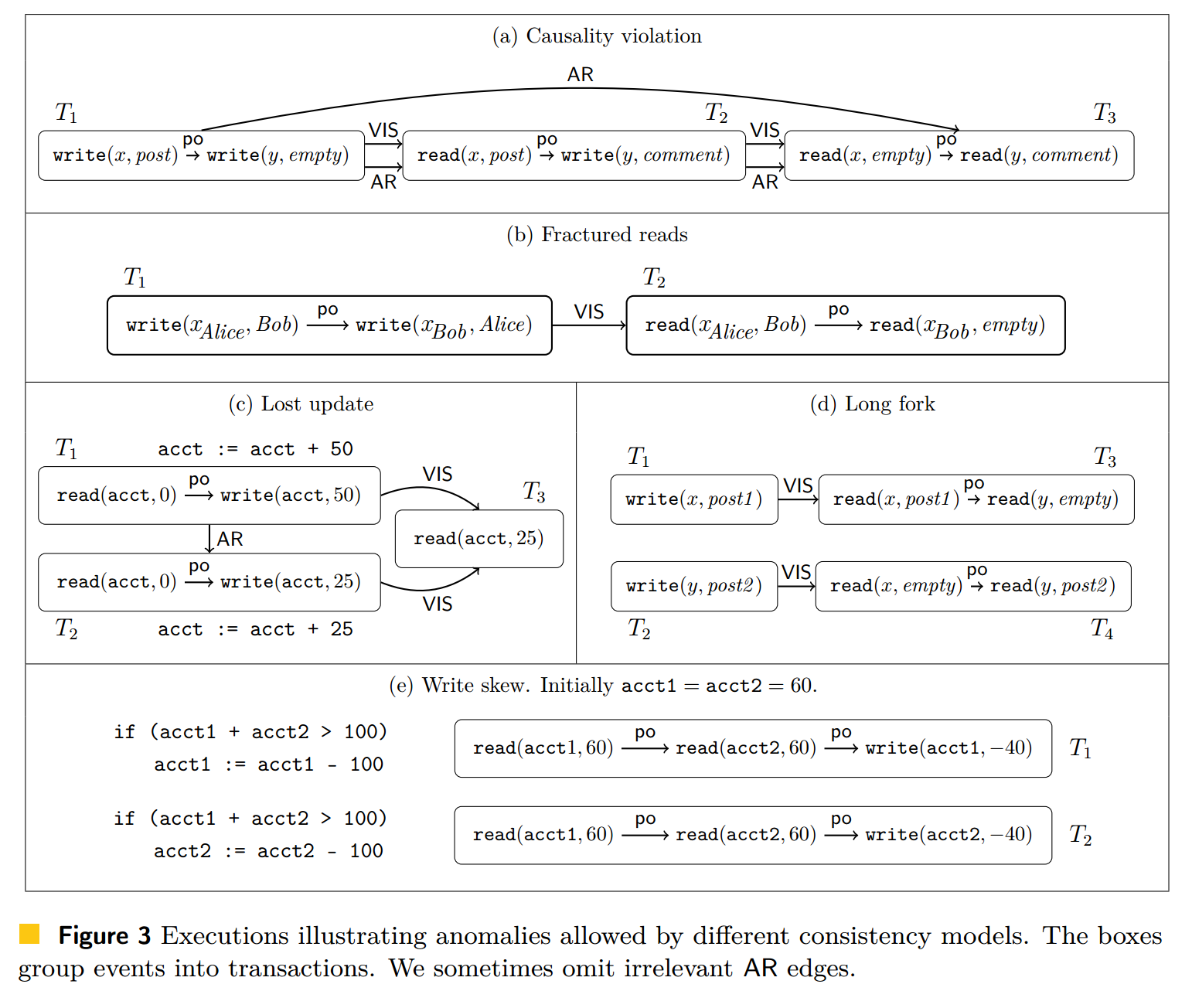
Operational Specifications
Operational Specification of Read Atomic
Correspondence to Axiomatic Specifications and Other Models
Related Work
我们的规范框架建立在公理化方法之上,用于指定一致性模型,该方法先前已应用于弱共享内存模型[3]和最终一致性[11,12]。特别是,可见性和仲裁关系最初是为了指定最终一致性和因果一致事务[12]而引入的。与之前工作相比,我们处理了更复杂的事务一致性模型。此外,我们的框架专门针对具有原子可见性的事务模型,通过在事务整体而非事件上定义可见性和仲裁关系。这避免了在所有公理中明确强制执行原子可见性[12]的需要,从而简化了规范。
Adya[2]先前为经典数据库中的弱一致性事务模型提出了规范。他的框架也广泛遵循公理化规范方法,但使用了与可见性和仲裁不同的关系。Adya 的工作没有解决最近为大规模数据库提出的各种一致性模型,而我们的框架特别适合这些模型。另一方面,Adya 处理了不保证原子可见性的事务一致性模型,例如已读提交(Read Committed),我们没有涉及这一点。Adya 还指定了快照隔离(SI),这是我们考虑的其他模型中较老的一种弱一致性模型。然而,他的规范是低级别的,因为它引入了额外的事件来表示事务获取数据库状态快照的时间。Saeida Ardekani 等人[22]此后提出了一个更高层次的快照隔离规范;这个规范仍然使用单个事件的关系,因此没有利用原子可见性。
偏序已被用于定义并发和分布式程序的语义,例如通过事件结构[26]。我们的结果通过考虑事件之间的新类型关系来扩展这一研究方向,这些关系适合描述弱一致数据库的计算,并通过将生成的抽象规范与低级算法相关联。
先前的研究已经调查了通过消息传递进行通信的事务演算:cJoin[10]、TCCS”[17] 和 RCCS[15]。尽管复制数据库实现和我们的操作规范也基于消息传递,但我们考虑的数据库接口只允许客户端程序读写对象。因此,它为程序提供了共享内存的(不完美)幻觉,我们的目标是为这个接口提供规范,这些规范抽象于其基于消息传递的实现。
Conclusion
我们已经提出了一个框架,用于统一指定现代复制数据库的事务一致性模型。我们框架的公理性质使得规范声明性和简洁性,并通过利用原子可见性进一步简化。我们通过指定几个现有的一致性模型来说明该框架的使用,从而系统化了关于它们的知识。我们还通过证明我们的公理规范与更接近实现的操作规范等价,来验证我们的公理规范。
我们希望我们的工作能够促进大规模数据库和并发理论研究社区之间的思想交流。特别是,我们的框架提供了一个基础,用于开发关于使用现代数据库的应用程序正确性的推理技术;这是我们正在进行的工作的主题。
最后,公理规范非常适合系统地探索一致性模型的设计空间。特别是,规范提供的见解可能会建议新的模型,正如我们在 $\S 3$ 中通过更新原子模型所说明的那样。这可能会有助于设计复制数据库开始提供的复杂编程接口,以补偿其一致性模型的弱点。例如,所谓的复制数据类型[23]通过最终合并并发更新来避免丢失更新,而无需在副本之间进行协调,会话[25]为同一客户端发出的事务提供额外的一致性保证。最后,还有一些接口允许程序员为不同的事务请求不同的一致性模型[18],类似于弱内存模型中的栅栏[3]。未来我们计划推广我们的技术来处理上述特性。我们希望通过将我们的框架与[11]中提出的它们的规范集成来处理复制数据类型,并通过研究可见性和仲裁关系上的附加约束来处理会话和混合一致性模型。我们相信数据库一致性模型的复杂性以及上述编程接口使得正式和声明性地指定它们变得不可或缺。我们的工作为实现这一点提供了必要的基础。
其他材料
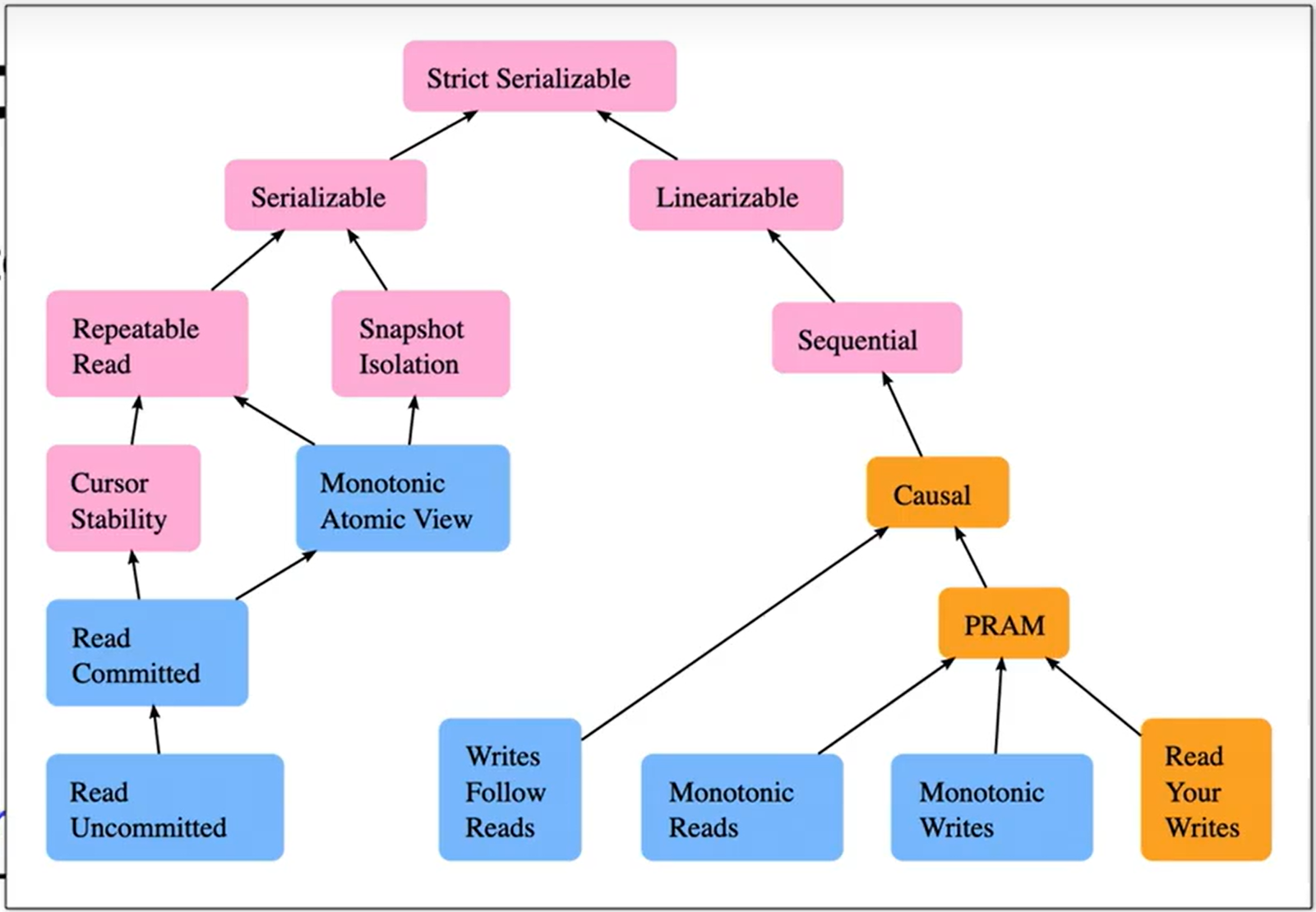
Gotsman 在 Database Isolation Levels Part 1 (SPTDC; Alexey Gotsman)_哔哩哔哩_bilibili 中用下图描述所有的隔离级别。