$$ \def\ReadSet{\mathsf{ReadSet}} \def\WriteSet{\mathsf{WriteSet}} \def\Attr{\mathsf{Attr}} \def\Account{Account} \def\Savings{Savings} \def\Checking{Checking} \def\Balance{Balance} \def\Amalgamate{Amalgamate} \def\Var{\mathsf{Var}} \def\Tuples{\mathsf{Tuples}} \def\prefix{\mathsf{prefix}} \def\postfix{\mathsf{postfix}} \def\ww{\mathsf{ww}} \def\rw{\mathsf{rw}} \def\wr{\mathsf{wr}} \def\pcfg{\mathsf{prefix-conflict-free-graph}} \def\R{\mathsf{R}} \def\W{\mathsf{W}} \def\U{\mathsf{U}} \def\t{\mathsf{t}} \def\v{\mathsf{v}} \def\T{\mathcal{T}} \def\P{\mathcal{P}} \def\D{\mathrm{D}} \def\C{\mathrm{C}} $$
摘要
众所周知,许多数据库系统提供的隔离级别多版本读取已提交 (RC) 会牺牲一致性来换取更高的事务吞吐量。有时,事务工作负载可以在 RC 下安全执行,以较低的 RC 成本获得完美的可序列化隔离。为了识别这种情况,我们引入了一个事务程序的表达模型,以更好地推理事务工作负载的可序列化性。**我们开发了易处理的算法来决定在 RC 下执行的工作负载的任何可能调度是否可序列化(称为稳健性问题)。**我们的方法产生的稳健子集比以前的方法识别的子集更大。我们提供实验证据表明,与更强的隔离级别相比,在 RC 下可以更快地评估对 RC 具有稳健性的工作负载。我们讨论了通过将选择性读取操作提升为更新来使工作负载对 RC 具有稳健性的技术。根据场景的不同,性能改进可能相当可观。因此,在较低的隔离级别 RC 下进行稳健性测试和安全地执行事务可以提供一种直接的方法来增加事务吞吐量,而无需更改 DBMS 内部结构。
作者:
- Brecht Vandevoort, UHasselt, Data Science Institute, ACSL, Belgium
- Bas Ketsman, Vrije Universiteit Brussel, Belgium
- Christoph Koch, École Polytechnique Fédérale de Lausanne, Switzerland
- Frank Neven, UHasselt, Data Science Institute, ACSL, Belgium
INTRODUCTION
关系数据库系统通过提供多种隔离级别,从而能够以隔离保证换取更高的性能,最高隔离级别是可序列化,它保证了被认为是完美的隔离。在较弱的隔离级别下并发执行事务并非没有风险,因为它可能会引入某些异常。但有时,一组事务可以在低于可序列化的隔离级别下执行,而不会引入任何异常。这是一种理想的情况:较低的隔离级别通常可以用更便宜的并发控制算法实现,它为我们免费提供了更强的可序列化隔离保证。这种正式的属性称为健壮性 [10, 21]:如果在指定的隔离级别下允许的 T 中所有可能的事务交错都是可序列化的,则称一组事务 T 对给定的隔离级别具有健壮性。
有一个著名的例子是数据库传说的一部分:TPC-C 基准 [46] 对快照隔离 (SI) 具有很强的鲁棒性,因此如果工作负载只是 TPC-C,则无需运行比 SI 更强大且更昂贵的并发控制算法。这在错误地选择 SI 作为 Oracle 和 PostgreSQL 中可序列化隔离级别的通用并发控制算法(9.1 版之前,参见 [22])方面发挥了一定作用。
一般来说,鲁棒性是一种无法判定的属性,因此以前的工作只处理了非常简单的工作负载模型。在本文中,我们专注于推动 RC 鲁棒性问题的前沿。任意数据库应用程序代码的鲁棒性都需要最先进的程序分析和定理证明器的全面复杂性,并且不允许我们提取可以导致更简单的分析算法的一般保证。我们采取了中间路线,提出了一种比以前考虑的更具表现力的工作负载模型,这让我们仍然可以制定一个完整且易于处理的鲁棒性决策程序。我们将通过示例(特别是 TPC-C 和 SmallBank 基准)展示我们的模型使我们能够显着扩展鲁棒性测试的范围,以 RC 隔离为代价为更大类别的工作负载提供保证的可序列化性。
我们的方法以 [21, 29] 为中心,以对 RC 鲁棒性的一种新表征为中心,这种表征改进了 [5] 中提出的充分条件,并以交易程序的形式化(称为交易模板)为中心,促进对 RC 鲁棒性的细粒度推理。我们形式化的关键方面如下:
- 从概念上讲,事务模板是带有参数的函数,例如,可以从数据库系统内的存储过程派生而来。我们的抽象概括了并发控制研究中通常研究的事务——读写操作序列——通过使工作对象变为变量,由输入参数决定。这些参数被输入以增加分析的额外能力。
- 我们支持原子更新(即,使用原子的 U 操作代替两个连续的 R-W 操作,对同一数据库对象进行读取后写入,以对其值进行相对更改),这使我们能够将一些原本不可靠的工作负载识别为可靠的。
- 此外,我们在字段粒度上对读写数据库对象进行建模,而不仅仅是整个元组,从而进一步解耦冲突并允许识别在元组级别上无法识别为可靠的其他情况。
该模型也有一些限制。我们假设有一组固定的只读属性,这些属性无法更新,用于选择要更新的元组。最典型的例子是作为参数传递给事务模板的主键值。在许多工作负载中,无法更新主键并不是一个重要的限制,因为出于监管或数据完整性的原因,一旦分配了键,就永远不会更改。一般来说,这种对更新和基于查询的相同字段选择的限制处理了这样一个事实:幻影问题的静态工作负载级分析很快就会产生不可判定性。这使得我们的结果在某些情况下不适用,但这些假设对于使这种多功能工作负载的稳健性可判定是必要的,而且获得这样的结果似乎是一个可以接受的权衡。可以希望未来的工作将进一步推动这一可判定性前沿。这些选择在易处理性和建模能力以及决定更现实的工作负载的稳健性之间提供了有趣的权衡,正如本文其余部分所讨论和说明的那样(如第 2 节中的 SmallBank 基准)。
总而言之,本文的技术贡献如下。
- 我们为纯粹事务实例的工作负载提供了针对 RC 的鲁棒性的完整描述(即,在没有变量的情况下)。该特征构成了下面(3)中提到的事务模板稳健性结果的主要构建模块。我们的结果本身就很有趣,因为已知完整特征的隔离水平并不多。Fekete [21]的开创性论文是第一篇为 SI 提供描述的论文。最近,在基于锁而不是多版本语义下为 RC 和 Read Uncommitted 获得了此类特征[29]。事实上,已经表明,在基于锁的语义下,针对 RC 的鲁棒性是一致完全的,这应该与本文获得的多版本读提交的多版本时间算法进行对比。
- 我们引入了事务模板的形式主义,并正式定义如何定义关联的工作负载集。新的形式化定义考虑了操作中变量的类型,使原子更新显式,并以字段而不是二元组的粒度对读取和写入的数据库对象进行建模。
- 我们获得了针对由事务模板定义的事务工作负载的 RC 鲁棒性的多项时间决策过程。这是第一次获得在交易程序层面上针对 RC 的稳健性的健全且完整的算法——也就是说,一种不会产生假阳性或假阴性的算法。通过这种方式,我们扩展了[5]中的工作,该工作基于鲁棒性的充分条件,即假阳性永远不会发生,但假阴性会发生。我们在第 8 节中详细讨论了算法的含义。
- 我们通过分析 SmallBank 和 TPC-Courier(基于 TPC-C)来评估我们方法的有效性,表明我们可以识别比之前方法识别的子集更大的稳健子集。尽管如此,在考虑所有交易模板时,SmallBank 和 TPC-Courier 都无法对抗 RC。我们考虑通过促进选择性读取操作来更新操作来使事务模板稳健的方法,并评估该方法在两个基准上的有效性。通过这些(保存)调整,两个完整的基准对 RC 来说变得稳健。
- 我们通过实验证明,使用这两个基准测试和一个众所周知的且未修改的数据库管理系统,与在 SI 或可序列化 SI 下执行时相比,以及与 RC 的其他鲁棒性技术相比,我们的方法带来了实际的性能改进[5],特别是在竞争较高的情况下。
由于空间限制,证明已推迟到本文的在线完整版本[47]。
MOTIVATING EXAMPLE
SmallBank [3]模式由帐户表(Name,CustomerID)、储蓄表(CustomerID,Balance)和支票表(CustomerID,Balance)组成(关键属性加了星号)。帐户表将客户名称与 ID 关联。其他表包含由 ID 标识的客户的储蓄和支票账户的余额(数字值)。应用程序代码通过以下交易程序与数据库交互:
Balance(N)返回名称为 N 的客户的总余额(储蓄和支票);DepositChecking(N, V)在姓名为 N 的客户的支票账户中存入金额为 V 的存款(参见图 1);TransactSavings(N, V)在姓名 N 的客户的储蓄账户上进行金额为 V 的存款或提款;Amalgamate(N1, N2)将所有资金从客户 N1 转移到客户 N2;WriteCheck(N, V)针对名为 N 的客户的账户开出金额为 V 的支票,如果透支则进行处罚。

Formalisation of transactions templates
图 2 显示了 SmallBank 的事务模板。事务模板由对特定关系中的元组 X 的一系列读、写和更新操作组成。
类型化变量有效地实施了域约束,因为我们假设在不同关系元组上的变量永远不能由相同的值实例化。
例如,在图 2 中 DepositChecking 的事务模板中,X 和 Z 不能被解释为相同的对象。

Detecting more robust subsets
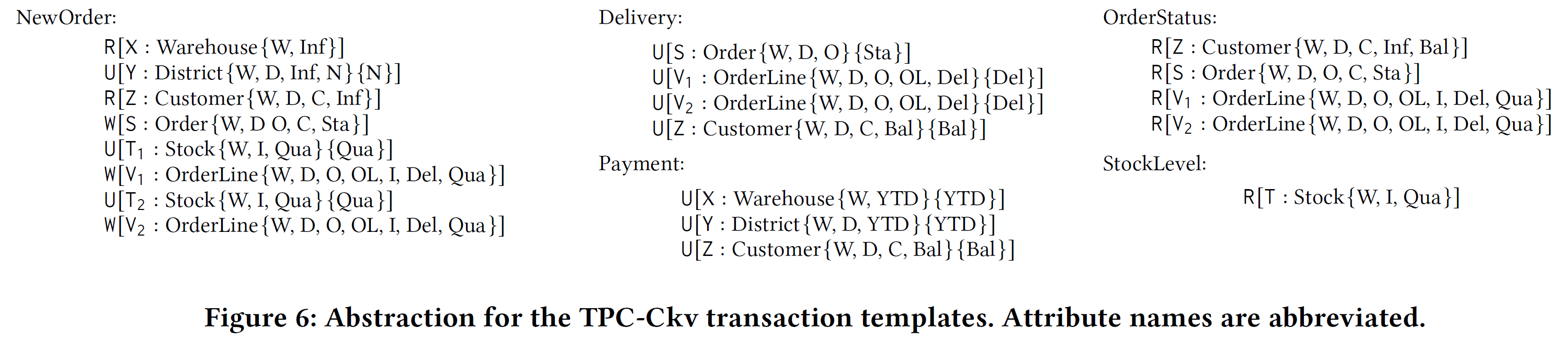
图 3 概述了使用我们的方法对 SmallBank 和 TPC-Ckv 基准测试检测到的最大鲁棒子集(TPC-Ckv 在第 7 节中讨论,模板在图 6 中给出)。交易模板以缩写形式呈现(例如,Bal 指的是 Balance)。为了评估抽象的不同特性的效果,我们考虑了不同的设置:
- “Only R & W”是通过读和写来建模更新的设置,其中读和写集总是指定整个属性集(也就是说,在整个元组级别上考虑冲突)。这个设置可以被看作是对应于[5]中的设置,它只报告集合 $\set{Bal}$ 对于 RC 是健壮的;
- “Atomic Updates”是将更新显式地建模为原子更新的扩展(即,使用原子的 U 操作代替两个连续的 R-W 操作),并且与“Only R & W”设置相比,已经允许检测相对较大的鲁棒集。实际上,对于 SmallBank 来说,$\set{Am,DC,TS}$ 是一个健壮的子集,表明任何调度使用任意数量的实例化,只要满足 RC 的这三个模板都是可序列化的!此外,对于 TPC-Ckv,检测到更大的鲁棒子集。
- “Attr conflicts”不再需要读写集来指定所有属性(也就是说,在属性级别上指定冲突)。为了说明其重要性,考虑操作 $R[X: Warehouse\set{W, Inf}]$ 和 $U[X: Warehouse\set{W, YTD}\set{YTD}]$分别来自图 6 所示的 TPC-Ckv 基准测试中的 NewOrder 和 Payment 模板。这两个模板在两个操作中将 X 映射到同一个元组 t 的实例化不会导致冲突,因为前者的读集与后者的写集是不相交的。然而,考虑到元组粒度上的冲突,即读写集引用所有属性,确实会导致冲突。这种粒度上的差异对 TPC-Ckv 有深远的影响,如图 3 的最后一行所示:发现了(从五个模板当中)四个模板的健壮子集:$\set{Del,Pay,NO,SL}$。对于 SmallBank 来说,没有改进,因为元组冲突总是意味着该基准的属性冲突,因为所有属性冲突都基于 Savings 和 Checking 中相同的 Balance 属性。我们将在第 8 节中解释属性级冲突的健壮性如何意味着并发控制子系统在元组粒度上工作的系统的健壮性。
以上三个条件逐渐放松,允许更多的并发行为,因此依次获得了更大的鲁棒子集。
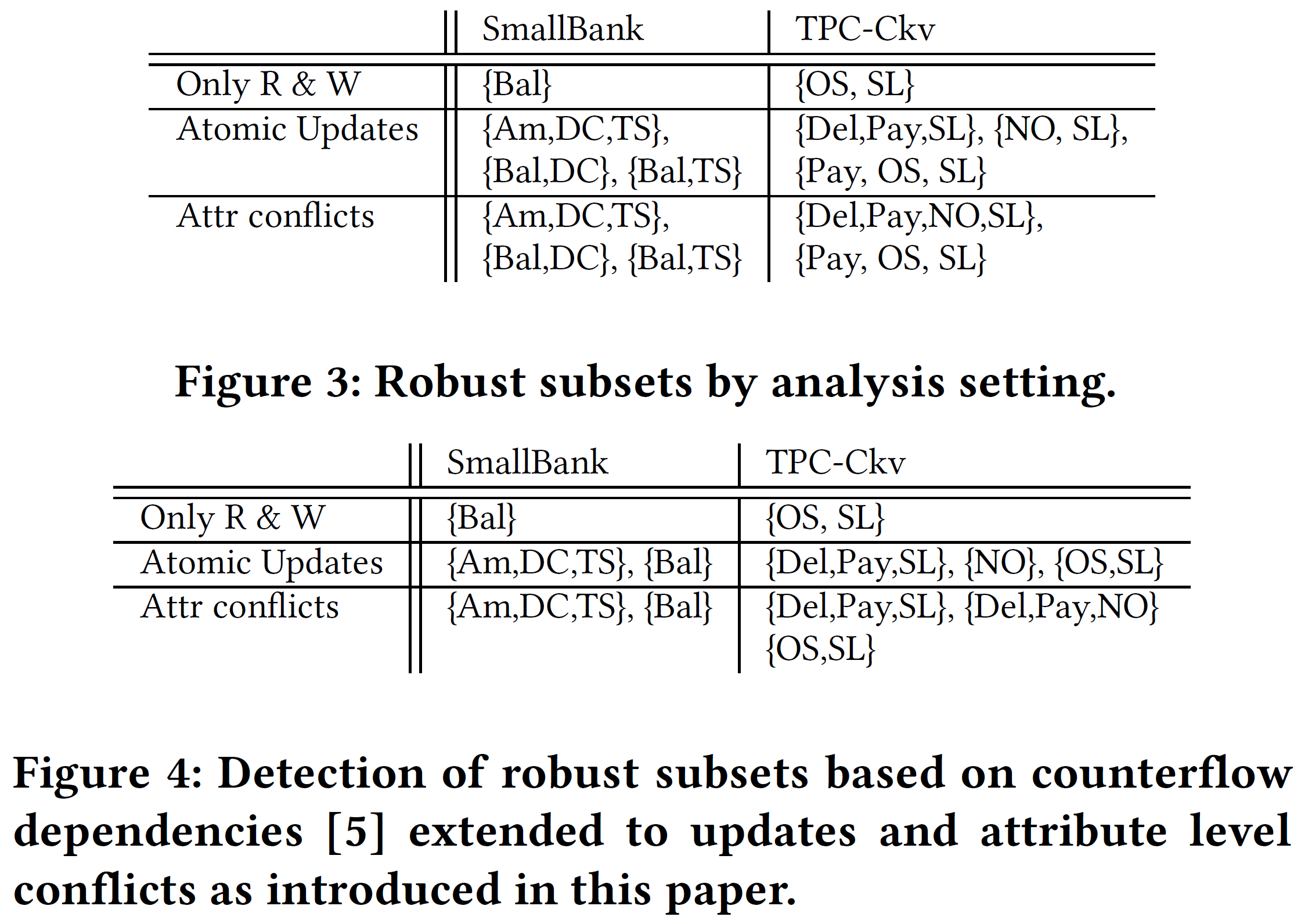
我们并不声称我们抽象中的所有特性都是新颖的。新颖之处在于它们的组合推动了 RC 稳健性问题的前沿。事实上,图 3 清楚地表明,当以明确的形式化方式结合在一起时,可以安全地确定更大的事务工作负载集是稳健的。这很重要,因为与 SI 或可序列化 SI 相比,在 RC 下可以以更高的吞吐量执行稳健工作负载(参见第 9.2 节)。
早期基于反向流依赖关系(counterflow dependency)的 RC 稳健性研究 [5] 没有考虑原子更新或属性级冲突,但可以扩展到这些设置。这些扩展检测到的稳健子集如图 4 所示。与图 3 的比较表明,尽管检测到了更大的子集,但我们的分析在“原子更新”和“属性冲突”下仍然检测到两个基准测试中更多甚至更大的稳健子集。
RELATED WORK
Static robustness checking on the application level
之前对事务程序的静态稳健性测试 [5, 22] 的研究基于以下关键见解:当一个调度不可序列化时,从该调度构建的依赖关系图包含一个满足特定于当前隔离级别的条件的循环:对于 SI 是危险结构,对于 RC 是逆流边的存在。这通过所谓的静态依赖关系图扩展到事务程序的工作负载,其中每个程序都由一个节点表示,如果存在导致冲突的调度,则从一个程序到另一个程序存在冲突边。没有满足特定于该隔离级别的条件的循环保证了稳健性,而存在循环并不一定意味着不稳健。我们通过在事务模板的形式化中更明确地阐明基本假设,提供了一种静态稳健性测试的形式化方法,并获得了一个可靠且完整的决策程序,可用于针对 RC 进行稳健性测试,从而可以检测出更大的事务子集是否稳健,如第 2 节所示。
其他工作研究了在以声明方式统一指定不同隔离级别的框架内的稳健性 [10, 13, 14]。这里的一个关键假设是原子可见性,要求每个事务的所有更新对其他事务都是可见的,或者对其他事务都不是可见的。这旨在实现更高的隔离级别,不能用于 RC,因为 RC 不承认原子可见性。
在较低隔离级别下执行非稳健工作负载通常会增加吞吐量,但代价是增加异常数量。为了更好地量化给定工作负载的这种权衡,Fekete 等人 [23] 提出了一个概率模型,该模型可以根据特定的工作负载配置预测完整性违规率。这条工作线与稳健性正交,因为稳健的工作负载将增加吞吐量而不会引入异常。
事务切割(transaction chopping)将事务拆分成更小的部分以获得性能优势,并且如果对于切割的每个可序列化执行,都存在原始事务的等效可序列化执行,则该操作是正确的 [42]。Cerone 等人 [14, 15] 研究了不同隔离级别下的切割。事务切割与针对 RC 的稳健性测试没有直接关系。
Making transactions robust
当工作负载对某个隔离级别不够稳健时,可以通过修改事务程序[2-5, 22]、使用外部锁管理器[2, 5, 6]、将某些程序分配到更高的隔离级别[4, 21],甚至结合使用这些技术[2]来实现稳健性。
对于 SI,已经研究了两种从静态依赖关系图中删除危险结构的代码修改技术 [2-4、6、22]:具体化和提升。具体化技术通过向数据库添加一个表示冲突的新元组来实现两个潜在并发事务之间的冲突,并将对该元组的写入添加到两个事务中,强制它们为非并发。或者,可以使用外部锁管理器 [6]。提升技术通过向同一对象添加标识写入来提升读取操作。在某些 DBMS 上,可以通过将 SELECT 语句更改为 SELECT ... FOR UPDATE 来实现提升。代码修改技术的替代方法是将一些事务分配给 S2PL 而不是 SI [21]。Alomari [2] 考虑了一种改进方法,即为在 S2PL 下运行的每个事务添加额外的写入。
对于 RC,Alomari 和 Fekete [5] 考虑使用两种方法实现锁实现,以避免反向流依赖:(1) 在数据库中,通过在每个事务开始时对新引入的元组添加写入;(2) 在数据库之外引入应用程序需要访问的外部锁管理器。相比之下,我们采用基于提升的代码修改技术,就像 SI 一样,将某些读取操作更改为更新。我们在第 9.3 节中提供了比较。
已经提出了许多提高事务吞吐量的方法:改进的或新颖的悲观算法(例如参见 [27、37、39、45、48])或乐观算法(例如参见 [11、12、17、18、25、26、28、30-32、34、40、41、49、50]),以及基于协调避免的方法(例如参见 [19、20、33、36、38、43、44])。我们不与这些方法进行比较,因为我们的重点在于一种可以应用于标准 DBMS 而无需对数据库内部进行任何修改的技术。
DEFINITIONS
Databases
Transactions and Schedules
元组 $t \in \Tuples$ 相当于关系型数据库当中的“行”。
$\R[t], \U[t], \W[t]$ 表示对元组 $t$ 的操作,其中前两种属于读操作,后两种属于写操作。此外还有 commit 操作。
$\ReadSet(o), \WriteSet(o)$ 表示操作 $o$ 所读到的、写入的属性(字段)的集合,而不是元组的集合。
事务形式化表示为 $(T, \le_T)$ ,其中 $T$ 表示操作的集合(包括读操作、写操作和 commit 操作),$\le_T$ 表示集合内的操作顺序,相当于执行历史中的 program order 边。
在事务集合 $\T$ 中有一个 id,用 $T_i$ 表示每个事务,其中 $i$ 是唯一的 id。$\W_i[t]$ 表示该操作属于 $T_i$。
事务集合 $\T$ 上的(多版本)调度用元组 $s=(O_s, \le_s, \ll_s, v_s)$ 表示。其中,
- $O_s$ 是 $\T$ 中所有操作的集合,并且还包括一个特殊的操作 $op_0$ 表示初始化写入;
- $\le_s$ 是这些操作的顺序;
- $\ll_s$ 是 version order,对所有同一个元组上的写操作进行排序,相当于依赖图当中的 ww 边;
- $v_s$ 是 version function,$v_s(a) = b$ 表示读操作 a 读取了写操作 b 写入的值。
对同一个元组上的两个写操作,$\ll_s$ 关系并不一定要与 $\le_s$ 一致。例如,在 RC 下,version order 是基于 commit order 的。
如果某调度 $s$ 中的 $\ll_s$ 关系与 $\le_s$ 关系一致,且读操作总是读取最近一个写操作,则该调度称为单版本调度。
Conflict Serializability
我们说 $a_j$ 和 $b_i$ 是冲突的,意味着三者之一:
- (ww-conflict) $\WriteSet(a_j) \cap \WriteSet(b_i) \neq \emptyset$;
- (rw-conflict) $\ReadSet(a_j) \cap \WriteSet(b_i) \neq \emptyset$;
- (wr-conflict) $\WriteSet(a_j) \cap \ReadSet(b_i) \neq \emptyset$。
定义 1
调度 $s$ 是冲突可串行化的,意味着该调度与某一个串行调度(single version serial schedule)冲突等价。
定理 2
调度 $s$ 是冲突客可串行化的,当且仅当其冲突依赖图无环。
Multiversion Read Committed
定义 3
某个调度在 RC 隔离级别下被允许,意味着它满足 RLC(read-last-committed) 并且不产生脏写。
Robustness
定义 4
一个事务集合 $\T$ 对于 RC 是健壮的,意味着其任何一个 RC 下的调度都是冲突可串行化的。
示例 5
对于调度 $s = \R_1[\t\set{a, b, c}] \R_2[\v\set{b}] \W_2[\t\set{a, b, d}] \C_2 \W_1[\v\set{a}] \C_1$,在元组冲突(tuple-conflict)级别下是不健壮的,在属性冲突(attribute-conflict)级别是健壮的。
ROBUSTNESS FOR TRANSACTIONS
在下一节介绍事务模板的形式化之前,我们首先研究事务的稳健性问题。本节的结果可作为事务模板稳健性算法的基础。
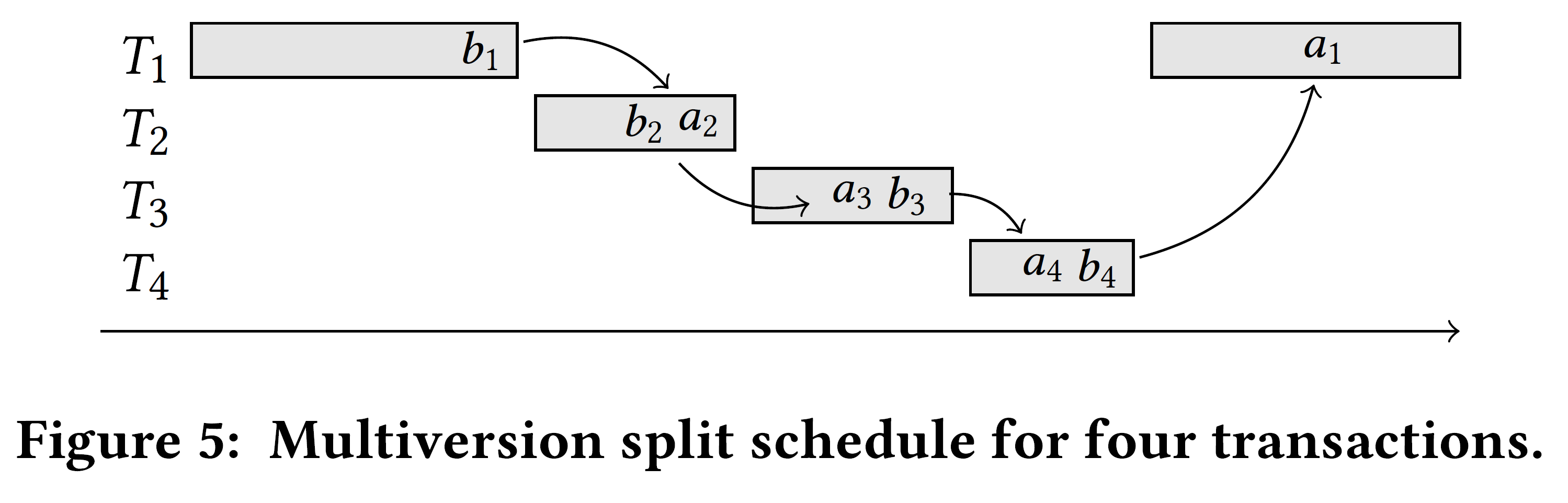
确定一组事务的稳健性属性的一种简单方法是遍历 RC 下允许的所有可能的调度,并验证没有一个违反冲突可序列化性。我们在本节中表明,只有具有非常特殊结构的调度才需要考虑,这些调度构成了可处理决策程序的基础。我们将这些调度称为多版本拆分调度。
定义 6 多版本拆分调度
对于事务集合 $\T$ 和 $\T$ 的一个冲突四元组序列 $C = (T_1, b_1, a_2, T_2), (T_2, b_2, a_3, T_3), \dots, (T_m, b_m, a_1, T_1)$,$\T$ 中的每个事务在 $C$ 中都最多出现两次。$\T$ 的一个基于 $C$ 的多版本拆分调度有如下形式:
$$ \prefix_{b_1}(T_1) \cdot T_2 \cdot ... \cdot T_m \cdot \postfix_{b_1}(T_1) \cdot T_{m+1} \cdot ... \cdot T_n $$
其中:
- $\prefix_{b_1}(T_1)$ 和 $T_2, \dots , T_m$ 中的操作都没有 $\ww$ 冲突(不允许脏写,允许有 $\wr$ 冲突,但该冲突并不会导致 $\wr$ 依赖边,因为 RLC);
- $b_1 <{T_1} a_1$ 或者 $b_m$ 和 $a_1$ 有 $\rw$ 冲突(若 $a_1 <{T_1} b_1$,则 $b_m \to a_1$ 只能是 $\rw$,因为 $T_1$ 中未提交的写对其他事务不可见);
- $b_1$ 和 $a_2$ 有 $\rw$ 冲突(该冲突必然对应 $\rw$ 依赖边)。
此外,$T_{m+1}, \dots , T_n$ 是 $\T$ 中剩余的事务,它们未在 $C$ 中出现,以任意顺序排列(因为这些事务不涉及冲突)。
其中,条件 1 保证了调度 $s$ 满足 RC,条件 2 和 3 保证了 $C$ 和某个 $CG(s)$ 中的环对应。
以下定理根据多版本拆分调度的存在性来描述非鲁棒性。证明表明,对于 RC 下允许的任何反例调度(反例调度的意思是违反 SER 的调度吗?),都可以构造一个反例调度,即多版本拆分调度,反之,任何多版本拆分调度 $s$ 都会在冲突图 $CG(s)$ 中产生循环。
定理 7
对于一组事务 $\T$,这两者等价:
- $\T$ 对 RC 不健壮;
- 存在基于某个冲突四元组序列 $C$ 的 $\T$ 多版本拆分调度 $s$。
该定理应该这样理解:由于我们知道不健壮的充要条件是某个调度存在依赖环,该定理意味着若某调度存在依赖环,则必然存在另一个包含上述冲突四元组序列 C 调度。
RC 下鲁棒性的上述特性导致了一个多项式时间复杂度的算法,环绕所有可能的拆分调度。对此,我们需要引入如下记号:对于事务 $T_1$,操作 $b_1 \in T_1$ 和事务集合 $\T$,其中 $T_1 \notin \T$,定义 $\pcfg(b_1, T_1, \T)$ 是一个图,将 $\T$ 中所有与 $\prefix_{b_1}(T_1)$ 中操作没有 ww 冲突的事务作为结点。如果 $T_i$ 和 $T_j$ 中的操作冲突,则在 $T_i$ 和 $T_j$ 间存在边。
定理 8
算法 1 可判断事务集合 $\T$ 在 RC 下是否鲁棒,时间复杂度为 $O(\max\set{k\left|\T\right|^3, k^3 l})$,其中 $k$ 是 $\T$ 中总操作数,$l$ 是 $\T$ 中每个事务的最大操作数。
TRANSACTION TEMPLATES
交易模板是针对类型变量定义操作的交易。变量类型是 Rels 中的关系名称,表示变量只能由相应类型的元组实例化。
我们固定一个无限的变量集 $\Var$,该集与 $\Tuples$ 不相交。每个变量 $X \in \Var$ 在 $\mathsf{Rels}$ 中有一个与之关联的关系名作为类型,我们用 $\mathsf{type}(X)$ 表示。
定义 9
一个事务模板 $\tau$ 是在 $\Var$ 上的事务。此外,对于 $\tau$ 中的每个操作 $o$,如果 $o$ 在变量 $X$ 上操作,则 $\ReadSet(o) \subseteq \Attr(\mathsf{type}(X))$ 和 $\WriteSet(o) \subseteq \Attr(\mathsf{type}(X))$。
请注意,事务模板中的操作定义在类型化的变量上,而事务中的操作则定义在 $\Tuples$ 上。实际上,图 2 中的 Balance 事务模板包含一个读操作 $o = \R[X : \mathsf{Account}\set{N, C}]$。如第 2 节所述,记号 $X : \mathsf{Account}\set{N, C}$ 是 $\mathsf{type}(X) = \mathsf{Account}$ 和 $\ReadSet(o) = \set{N, C}$ 的缩写。
回忆一下,我们用大写字母 $X, Y, Z$ 表示变量,用小写字母 $\t, \v$ 表示元组。变量赋值 $\mu$ 是从 $\Var$ 到 $\Tuples$ 的映射,使得 $\mu(X) \in \Tuples_{\mathsf{type}(X)}$。通过 $\mu(\tau)$,我们表示通过将 $\tau$ 中的每个变量 $X$ 替换为 $\mu(X)$ 获得的事务。数据库 $\D$ 的变量赋值将每个变量映射到 $\D$ 中关系中的元组。
一组事务 $\mathcal{T}$ 与一组事务模板 $\mathcal{P}$ 和数据库 $\D$ 一致,如果对于 $\mathcal{T}$ 中的每个事务 $T$,存在一个事务模板 $\tau \in \mathcal{P}$ 和一个变量赋值 $\mu_T$ 对于 $\D$,使得 $\mu_T(\tau) = T$。
令 $\mathcal{P}$ 为一组事务模板,$\D$ 为一个数据库。那么,$\mathcal{P}$ 在 $\D$ 上对 RC 是鲁棒的,如果对于与 $\mathcal{P}$ 和 $\D$ 一致的每组事务 $\mathcal{T}$,$\mathcal{T}$ 对 RC 是鲁棒的。
定义 10(鲁棒性)
一组事务模板 $\P$ 在所有数据库 $\D$ 上对 RC 是鲁棒的,如果 $\P$ 在每个数据库 $\D$ 上对 RC 是鲁棒的。
示例 11
考虑基于 SmallBank 模式的小型数据库 $\D$:$\Account^\D = \set{a_1, a_2}$; $\Savings^\D = \set{s_1, s_2}$; 和 $\Checking^\D = \set{c_1, c_2}$。
为了简化,我们忽略读写集。设 $\T_1 = \set{\R[a_1] \R[s_1] \R[c_1], \R[a_1] \R[a_2] \U[s_1] \U[c_1] \U[c_2]}$。那么 $\T_1$ 与 SmallBank 事务模板和 $\D$ 一致,如事务模板 Balance 和 Amalgamate 以及变量赋值 $\mu_1 = \set{X \rightarrow a_1, Y \rightarrow s_1, Z \rightarrow c_1}$ 和 $\mu_2 = \set{X_1 \rightarrow a_1, X_2 \rightarrow a_2, Y_1 \rightarrow s_1, Y_2 \rightarrow s_2, Z_2 \rightarrow c_2}$ 所示。集合 $\set{\Balance, \Amalgamate}$ 在 $\D$ 和 $\T_1$ 上对 RC 不是鲁棒的。
实际上,我们可以构造一个多版本拆分调度 $\T_1$:
$$ \begin{aligned} T_1: & \R_1[a_1] \R_1[s_1] & & \R_1[c_1] \C_1 \ T_2: & & \R_2[a_1] \R_2[a_2] \U_2[s_1] \U_2[c_1] \U_2[c_2] \C_2 & \end{aligned} $$
ROBUSTNESS FOR TEMPLATES
Algorithm 1 不能直接应用于测试事务模板的鲁棒性,因为与给定的一组事务模板 $\P$ 一致的事务集 $\T$ 有无限多个。我们采用了一种不同的方法,类似于 Algorithm 1,但直接在事务模板上操作。
在提出的算法(Algorithm 2)中,核心是对冲突操作的泛化:对于事务模板 $\tau_i$ 和 $\tau_j$ 中的操作 $o_i$ 和 $o_j$,我们说 $o_i \in \tau_i$ 与 $o_j \in \tau_j$ 潜在冲突,如果 $o_i$ 和 $o_j$ 是对同一类型变量的操作,并且至少满足以下条件之一:
- $\WriteSet(o_i) \cap \WriteSet(o_j) \neq \emptyset$(潜在 ww-冲突);
- $\WriteSet(o_i) \cap \ReadSet(o_j) \neq \emptyset$(潜在 wr-冲突);
- $\ReadSet(o_i) \cap \WriteSet(o_j) \neq \emptyset$(潜在 rw-冲突)。
直观上,潜在冲突的操作在这些操作的变量通过变量赋值映射到同一个元组时会导致冲突操作。类似于在 Definition 6 中定义的事务集上的冲突四元组,我们考虑事务模板集 $\P$ 上的潜在冲突四元组 $(\tau_i, o_i, p_j, \tau_j)$,其中 $\tau_i, \tau_j \in \P$,且 $o_i \in \tau_i$ 与 $p_j \in \tau_j$ 潜在冲突。一系列潜在冲突四元组 $D = (\tau_1, o_1, p_2, \tau_2), \ldots, (\tau_m, o_m, p_1, \tau_1)$ 通过应用变量映射 $\mu_i$ 到每个 $\tau_i$ 生成一系列冲突四元组 $C = (T_1, b_1, a_2, T_2), \ldots, (T_m, b_m, a_1, T_1)$。我们将这样的一组变量映射简单地称为对 $D$ 的变量映射,记为 $\bar{\mu}$,并写为 $\bar{\mu}(D) = C$。
一个基本的见解是:如果对于与一组事务模板 $\P$ 和数据库 $\D$ 一致的事务集 $\T$ 存在一个多版本分裂调度 $s$,并且 $s$ 满足 Definition 6 的属性,那么存在一个潜在冲突四元组序列 $D$,使得 $\bar{\mu}(D) = C$ 对于某个 $\bar{\mu}$。Algorithm 2 采用的方法是枚举序列 $D$ 以及映射 $\bar{\mu}$,以寻找满足 Definition 6 条件的 $\bar{\mu}(D)$。如果存在反例,Algorithm 2 最多需要每种类型三个元组来构造反例。我们通过将数字 1 到 3 分配给特定操作来编码这种选择。
为了遍历所有可能的序列 $D$,Algorithm 2 遍历可能的拆分事务模板 $\tau_1 \in \P$ 及其可能的操作 $o_1, p_1 \in \tau_1$,并依赖于一个称为 pt-prefix-conflict-free-graph$(o_1, p_1, h, \tau_1, \P)$ 的图。这里,$h \in \set{1, 2}$ 表示当 $h = 1$ 时,$\tau_1$ 的前缀和后缀使用每种类型的同一个元组,当 $h = 2$ 时,后缀使用每种类型的第二个元组。该图的节点是四元组 $(\tau, o, i, j)$,其中 $\tau \in \P$,$o \in \tau$,$i \in \set{1, 2, 3}$ 且 $j \in \set{\text{in}, \text{out}}$。这里,$i \in \set{1, 2, 3}$ 编码分配给 $\tau$ 中 $o$ 的元组。将有两种类型的边:(1) 内部边 $(\tau, o, i, \text{in}) \rightarrow (\tau, p, i', \text{out})$,这些边在同一事务 $\tau$ 内,指示从 $c_i$ 到 $c_{i'}$ 的选定元组版本如何变化(或保持不变);以及 (2) 外部边 $(\tau, o, i, \text{out}) \rightarrow (\tau', p, i', \text{in})$,这些边在不同实例的事务模板之间,编码一个潜在冲突的四元组 $(\tau, o, p, \tau')$,并保持选定元组的信息。
更正式地,图中的四元组节点 $(\tau, o, i, j)$ 满足以下属性:
(a) $i = 1$ 表示在 $\prefix_{o_1}(\tau_1)$ 中没有操作 $o_1' \in \prefix_{o_1}(\tau_1)$ 与 $o_1$ 在同一变量上,且 $o_1'$ 与 $o$ 在同一变量上的操作潜在地 ww-冲突。 (b) $i = h$ 表示在 $\prefix_{o_1}(\tau_1)$ 中没有操作 $o_1' \in \prefix_{o_1}(\tau_1)$ 与 $p_1$ 在同一变量上,且 $o_1'$ 与 $o$ 在同一变量上的操作潜在地 ww-冲突。
节点上的条件 (a) 和 (b) 确保 Definition 6 的条件 (1) 对于所有与特定元组选择一致的可能变量映射总是成立的。此外,两个节点 $(\tau, o, i, j)$ 和 $(\tau', o', i', j')$ 通过有向边连接,如果满足以下条件之一:
($\dagger$) $\tau = \tau'$,$j = \text{in}$,$j' = \text{out}$,且如果 $o$ 和 $o'$ 在 $\tau$ 中是同一变量上的操作,则 $i = i'$(即,在同一事务内保持不变,并且仅当 $o$ 和 $o'$ 不在同一变量上时才改变选定的元组版本);或,
($\ddagger$) $j = \text{out}$,$j' = \text{in}$,$i = i'$,且 $o$ 和 $o'$ 潜在地冲突(即,对于分裂调度中连续事务的 $b$ 和 $a$ 的类比,但这里定义为事务模板)。
定理 12
Algorithm 2 在时间 $O(k^4 \cdot \ell)$ 内决定一组事务模板 $\P$ 是否对 RC 是鲁棒的,其中 $k$ 是 $\P$ 中操作的总数,$\ell$ 是 $\P$ 中事务的最大操作数。
核心洞察:对于事务模板集合 $\P$,如果存在由模板中事务构成的违反 SER 的反例,则必然存在一个反例,其中每种元组不超过三个。

DETECTING ROBUST SETS
由于稳健模板集的每个子集也都是稳健的,因此可以通过首先在 P 本身上运行算法 2,然后在较小的子集上运行算法 2(如果需要),来检测工作负载 P 的最大稳健子集。尽管可能的子集数量呈指数级增长,但 P 预计会很小,并且可以在静态和离线分析阶段执行稳健性测试。
算法 2 可以完整地表征属性级粒度的稳健性。我们讨论了将这些结果用于并发控制子系统在元组粒度上工作的 DBMS 的后果。在这种情况下,RC 实现的隔离强度超过了实际需要,以确保我们的技术确定为稳健的工作负载上的可序列化性。
在这种情况下,有两种方法可以采用我们的决策程序。第一种方法是简单地将工作负载模型粗化到元组级别,方法是为每个操作设置元组所有属性的读写集。这样,我们的算法就可以在元组级粒度上给出正确而完整的答案。如第 2 节所述,图 3 中的“原子更新”行表示在 SmallBank 和 TPC-Ckv 的此方法下哪些集合是稳健的,以及与仅考虑读写相比,这种方法如何改进。
第二种方法是简单地使用属性级模型,并接受 DBMS 比必要的更为保守。当我们的算法确定工作负载是稳健的时,该工作负载在保证具有元组级数据库对象的 RC 的系统上仍然是稳健的,原因很简单,每个属性粒度上的冲突都意味着元组粒度上的冲突。因此,这些系统可以创建的每个调度都是在我们的 RC 定义下允许的。但是,当我们的算法确定工作负载不稳健时,它们可能过于保守:它们可能会通过识别一组完整的反例调度来做到这一点,而这些调度实际上可能都不被元组粒度的 RC 所允许。因此,我们的属性级算法在技术上仅提供了此类系统稳健性的充分条件,而不是完整条件。尽管如此,第二种技术在 SmallBank 和 TPC-Ckv 上严格优于第一种技术(如图 3 中“Attr 冲突”行所示),即使 DBMS 使用元组级对象。它检测前一种方法的所有稳健情况,以及可能只能通过属性级分析发现的其他情况,但在具有元组级并发控制的 DBMS 上仍然很稳健。后一种方法导致具有实用价值的更一般的观察结果:我们的算法为只能生成 RC 允许的调度子集的每个实现提供了充分条件来保证可串行化。
EXPERIMENTS
在第 2 节末尾,我们讨论了我们的方法在检测更大的稳健子集方面的有效性,并与 [5] 进行了比较。在这里,我们重点关注稳健性如何提高交易吞吐量。
Experimental Setup
Robust workloads
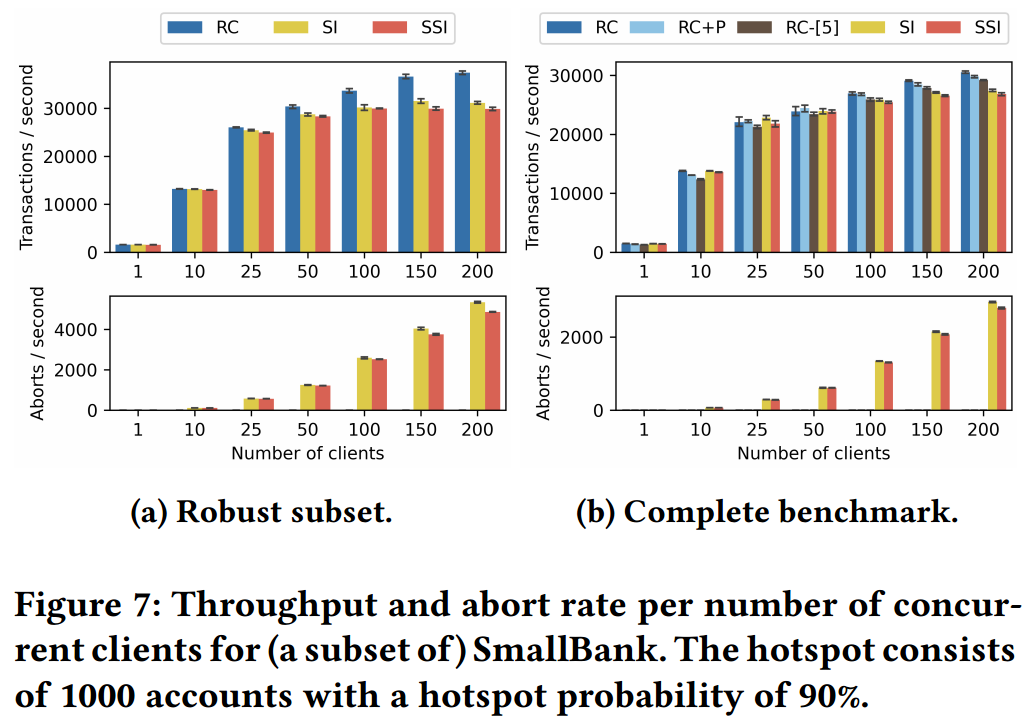
Promoted workloads