OOPSLA'19-On the Complexity of Checking Transactional Consistency

$$$$

摘要

事务通过启用对共享数据的计算来简化并发编程，这些共享数据与其他并发计算隔离并且对故障具有弹性。现代数据库为事务提供了不同的一致性模型，对应于一致性和可用性之间的不同权衡。在这项工作中，我们研究了检查事务数据库的给定执行是否遵循某种一致性模型的问题。我们证明了诸如读提交、读原子和因果一致性之类的一致性模型是多项式时间可检查的，而前缀一致性和快照隔离通常是 NP 完全的。这些结果补充了先前有关可串行性的 NP 完整性结果。此外，在 NP 完全一致性模型的背景下，我们设计了多项式时间的算法，假设输入执行中的某些参数（例如会话数）是固定的。我们在几个生产数据库的背景下评估这些算法的可扩展性。

笔者修改了 DBCop 的部分代码：https://git.nju.edu.cn/EagleBear/dbcop-verifier

作者：

• RANADEEP BISWAS, Universite de Paris, IRIF, CNRS, France
• CONSTANTIN ENEA, Universite de Paris, IRIF, CNRS, France

INTRODUCTION

事务通过启用对共享数据的计算来简化并发编程，这些共享数据与其他并发计算隔离并且能够适应故障。现代数据库提供各种形式的事务，对应于一致性和可用性之间的不同权衡。最强级别的一致性是通过可序列化事务实现的[Papadimitriou 1979]，其并发执行的结果与按某种顺序原子执行事务相同。不幸的是，串行化对系统的可用性带来了严重的损失，例如，假设数据库是通过可能遭受分区或故障的网络访问的。因此，现代数据库通常对事务提供较弱的保证，通过弱一致性模型形式化，例如因果一致性[Lamport 1978]和快照隔离[Berenson et al 1995]。

提供事务的大型数据库的实现很难构建和测试。例如，分布式（复制）数据库必须考虑部分故障，其中某些组件或网络可能会发生故障并产生不完整的结果。确保容错依赖于难以设计和推理的复杂协议。黑盒测试框架 Jepsen [Kingsbury 2019] 在许多生产分布式数据库中发现了大量微妙的问题。

测试事务数据库提出了两个问题：（1）导出一组合适的测试场景，例如注入系统的故障和要执行的事务集，以及（2）导出有效的算法来检查给定的执行是否满足所考虑的一致性模型。 Jepsen 框架旨在通过使用随机化来解决第一个问题，例如随机引入故障并随机选择事务中的操作。这种方法的有效性已在最近的工作中得到正式证明 [Ozkan et al 2018]。然而，第二个问题基本上尚未得到探讨。 Jepsen 以一种相当特别的方式检查一致性，重点关注给定一致性模型的特定类别的违规，例如脏读（从中止的事务中读取值）。这个问题具有挑战性，因为一致性规范非常重要，并且无法使用例如添加到客户端代码中的标准本地断言来检查它们。

除了可串行化之外，检查执行正确性的复杂性也很复杂。某些一致性模型是未知的。检查可串行性已被证明是 NP 完全的 [Papadimitriou 1979]，并且在非事务上下文中检查因果一致性已知需要多项式时间 [Bouajjani et al 2017]。在这项工作中，我们试图通过调查这个问题的复杂性来填补这一空白。几个一致性模型，并且在 NP 完整性的情况下，设计多项式时间的算法，假设输入执行的某些参数（例如会话数）有固定界限。

我们考虑了实践中最流行的几种一致性模型。其中最弱的是提交读（RC）[Berenson et al 1995]，要求事务中读取的每个值都由提交的事务写入。读取原子（RA）[Cerone et al 2015] 要求在事务中连续读取同一变量返回相同的值（也称为可重复读取 [Berenson et al 1995]），并且事务“看到”前一个写入的值同一会话中的事务。一般来说，我们假设事务是在会话中组织的[Terry et al 1994]，会话是应用程序执行期间执行的事务序列的抽象。因果一致性（CC）[Lamport 1978] 要求如果事务 $t_1$ 影响另一个事务 $t_2$，例如，在同一会话中 $t_1$ 在 $t_2$ 之前排序，或者 $t_2$ 读取 $t_1$ 写入的值，则这两个事务可以被任何其他事务观察到按这个顺序。前缀一致性（PC）[Burckhardt et al 2015] 要求所有事务之间存在总提交顺序，以便每个事务都遵守该序列的前缀。快照隔离（SI）[Berenson et al 1995] 进一步要求两个不同的事务在都写入公共变量时观察不同的前缀。最后，我们还提供了有关检查可串行性（SER）问题的新结果，以补充有关其 NP 完整性的已知结果。

我们在本文中探讨的算法问题为这些一致性模型带来了一个新的规范框架，该框架依赖于执行中的写入-读取关系（也称为读取）这一事实，将读取与写入其数据的事务相关联。值，可以有效地定义。可以从每个值最多写入一次（变量可以写入任意次数）的执行中轻松提取写-读关系。这可以通过使用唯一标识符标记值来轻松实现（例如，随着每次新写入而递增的本地计数器与客户端/会话标识符相结合）1。由于实际的数据库实现是数据无关的[Wolper 1986]，即它们的行为不依赖于事务中读取或写入的具体值，因此任何潜在的错误行为都可能在每个值最多写入一次的执行中暴露出来。因此，这个假设不失一般性。

之前的工作 [Bouajjani et al 2017; Burckhardt et al 2014; Cerone et al 2015] 使用两种辅助关系形式化了这种一致性模型：为每个事务定义其观察到的事务集的可见性关系，以及定义事务提交到“全局”内存的顺序的提交顺序。满足某些一致性模型的执行被定义为存在可见性关系和遵守某些公理的提交顺序。在我们的例子中，从执行中导出的写-读关系扮演了可见性关系的角色。这种简化使我们能够陈述一系列定义这些一致性模型的公理，这些模型具有共同的形状。直观上，它们定义了事务 $t_1$ 集合的下限，该组事务 $t_1$ 必须按提交顺序位于执行中读取的事务 $t_2$ 之前。除了揭示这些一致性模型之间的差异之外，这些公理对于我们随后研究的算法问题也至关重要。

我们确定检查执行是否满足 RC、RA 或 CC 是多项式时间，而同样的问题对于 PC 和 SI 来说是 NP 完全的。此外，在 NP 完全一致性模型（PC、SI、SER）的情况下，我们表明，只要输入执行中的会话数被认为是固定的（即， 不计入输入大小）。更详细地说，我们确定，当会话数量固定时，检查 SER 可以简化为具有多项式大小的空间中的搜索问题。 （该算法适用于任意执行，但其复杂性一般来说会以会话数量呈指数级增长）然后，我们表明，使用执行转换，可以在多项式时间内将检查 PC 或 SI 减少为检查 SER，粗略地说， ，将每个事务分为两部分：一部分包含所有读取，一部分包含所有写入（SI 还需要添加一些额外的变量，以便处理在公共变量上写入的事务）。我们通过依赖称为通信图的执行抽象来进一步扩展这些结果 [Chalupa et al 2018]。粗略地说，通信图的顶点对应于会话，边表示两个会话访问（读或写）同一个变量。我们证明，只要通信图的双连通分量具有固定大小，所有这些标准都是多项式时间可检查的。

我们对我们的算法在 CockroachDB [Cockroach 2019a] 的执行上进行了实验评估，该数据库声称实现了可串行性 [Cockroach 2019b]，但承认存在异常的可能性；Galera [Galera 2019a] 的文档包含关于是否实现快照隔离的相互矛盾的声明[Galera 2019b,c] 和 AntidoteDB [Antidote 2019a]，声称实现因果一致性 [Antidote 2019b]。我们的实施报告在所有情况下都违反了这些标准。我们发现 AntidoteDB 的一致性违规是新颖的，并且已得到其开发人员的证实。我们证明了我们的算法是高效且可扩展的。特别是，我们表明，尽管我们算法的渐近复杂度一般是指数级的（相对于会话数），但在实践中并没有执行最坏情况的行为。

总而言之，这项工作的贡献有四个方面：

• 我们开发了一个新的规范框架来描述常见的事务一致性标准（§2）；
• 我们证明检查 RC、RA 和 CC 是多项式时间，而检查 PC 和 SI 是 NP 完全的（§3）；
• 我们证明 PC、SI 和 SER 是多项式时间可检验的，假设输入执行的通信图具有固定大小的双连通分量（§4 和§5）；
• 我们对生产数据库生成的执行算法进行实证评估（§6）；

这些贡献结合起来形成了一个用于验证事务一致性模型的有效算法框架。据我们所知，我们是第一个研究大多数一致性模型的渐近复杂性的人，尽管它们在实践中很普遍。

其他材料可在 [Biswas 和 Enea 2019] 中找到。

CONSISTENCY CRITERIA

Histories

我们考虑一个存储一组变量 $\mathsf{<}!--swig0-->=\{x,y,\dots \}$。客户端通过发出由读和写操作形成的事务来与数据库交互。假设一组未指定的值 $\mathsf{Val}$ 和一组操作标识符 $\mathsf{OpId}$，我们让

$$\mathsf{Op}=\{{\mathsf{read}}_i(x,v),{\mathsf{write}}_i(x,v):i\in \mathsf{OpId},x\in \mathsf{<}!--swig0-->,v\in \mathsf{Val}\}$$

是读取值 $v$ 或将值 $v$ 写入变量 $x$ 的操作集。当操作标识符不重要时，我们会忽略它们。

定义 2.1。事务 $⟨O,\mathsf{po}⟩$ 是一组有限的操作 $O$ 以及 $O$ 上的严格全序 $\mathsf{po}$，称为程序顺序，program order。

我们使用 $t, t_1, t_2 \dots $ 来排列事务。事务 $t$ 中的读、写操作集分别由 $\mathsf{reads}(t)$，和 $\mathsf{writes}(t)$ 表示。事务集的扩展照常定义。另外，我们说事务 $t$ 写入变量 $x$，表示为 $t$ 写入 $x$，当 ${\mathsf{write}}_i(x,v)\in \mathsf{writes}(t)$ 对于某些 $i$ 和 $v$ 时。类似地，事务 $t$ 读取变量 $x$，当 ${\mathsf{read}}_i(x,v)\in \mathsf{reads}(t)$ 对于某些 $i$ 和 $v$ 来说。

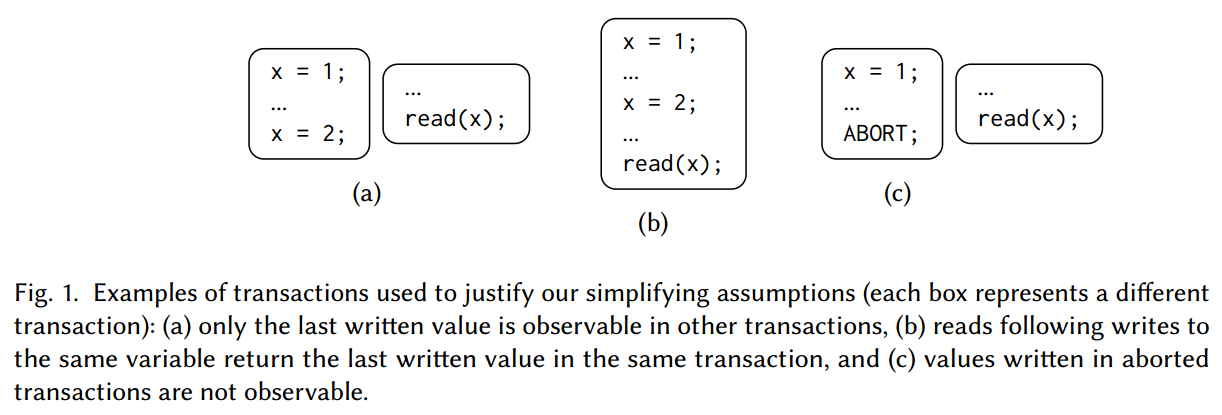
为了简化说明，我们假设每个事务 $t$ 至多包含对每个变量 $x$ 的一次写入操作，并且在同一事务中读取变量 $x$ 之前不能先写入 $x$（也即，不存在对于同一个变量“先写后读”）。如果一个事务包含对同一变量的多次写入，则只有最后一个对其他事务可见（相对于实践中考虑的任何一致性标准）。例如，图 1a 中的 $\mathsf{read}(x)$ 不应返回 1，因为这不是其他事务写入 $x$ 的最后一个值。它可以返回初始值或 2。此外，如果在同一事务中在读取之前先写入同一变量，那么它应该返回在同一事务中写入的值（即最新写入的值）事务中的 $x$。例如，图 1b 中的 $\mathsf{read}(x)$ 只能返回 2（假设同一事务中没有其他对 x 的写入）。这两个属性可以在给定的执行中轻松验证（以语法方式）。除了这两个属性之外，实践中使用的各种一致性标准仅约束每个事务中对每个变量的最后写入以及同一事务中不先于对同一变量的写入的读取。

一致性标准在称为历史（history）的执行的抽象视图上形式化。历史记录仅包含成功或已提交的事务。在数据库上下文中，始终假设中止事务的影响对其他事务不可见，因此可以忽略它们。例如，图 1c 中的 $\mathsf{read}(x)$ 不应返回由中止事务写入的值 1。事务根据（部分偏序）会话顺序（session order） $\mathsf{so}$ 进行排序，因此这表示使用数据库的应用程序施加的排序约束。最常见的是序列的并集，每个序列称为一个会话。我们假设历史记录包含 W-R 关系，该关系标识写入执行中每次读取返回的值的事务。如前所述，可以从每个值最多写入一次的执行中轻松提取这样的关系。由于在实践中，数据库是数据独立的 [Wolper 1986]，即它们的行为不依赖于事务中读取或写入的具体值，因此在此类执行中可能会暴露任何潜在的错误行为。

定义 2.2。历史 $⟨T,\mathsf{so},\mathsf{wr}⟩$ 是一组事务 $T$ 以及严格的偏序（称为会话顺序），以及关系 $\mathsf{wr}\subseteq T\times \mathsf{reads}(T)$ 称为写-读关系，当且仅当

• $\mathsf{wr}$ 的反函数是一个全函数（total function），如果 $(t,\mathsf{read}(x,v))\in \mathsf{wr}$，则 $\mathsf{write}(x,v)\in t$，并且
• $ \so \cup \wr$ 是无环的。

全函数意味着每一个读操作读到的值都对应着对该变量的更早的一个写操作。

为了简化技术说明，我们假设每个历史记录都包含写入所有变量初始值的不同事务。此事务先于 $\mathsf{so}$ 中的所有其他事务。我们使用 $h,h_1,h_2,\dots$ 涵盖历史。

当 $(t,\mathsf{read}(x,v))\in \mathsf{wr}$ 时，我们说读操作 $\mathsf{read}(x,v)$ 从 $t$ 写入的变量 $x$ 中读取值 $v$。对于给定的变量 $x$，${\mathsf{wr}}_x$ 表示 $\mathsf{wr}$ 对变量 $x$ 的读取的限制，即，${\mathsf{wr}}_x=\mathsf{wr}\cap (T\times \{\mathsf{read}(x,v)|v\in \mathsf{Val}\})$（即，涉及到变量 $x$ 的 W-R 关系）。此外，我们将关系 $\mathsf{wr}$ 和 ${\mathsf{wr}}_x$ 扩展为事务对，如下所示：$⟨t_1,t_2⟩\in \mathsf{wr}$ 时，$⟨t_1,t_2⟩\in {\mathsf{wr}}_x$，当且仅当存在读操作 $\mathsf{read}(x,v)\in \mathsf{reads}(t_2)$ 使得 $⟨t_1,\mathsf{read}(x,v)⟩\in \mathsf{wr},⟨t_1,\mathsf{read}(x,v)⟩\in {\mathsf{wr}}_x$。当 $⟨t_1,t_2⟩\in \mathsf{wr}$ 时，我们说事务 $t_1$ 被事务 $t_2$ 读取，当它被某个事务 $t_2$ 读取时，我们说它被读取。

Axiomatic Framework

我们描述了一个公理框架来描述满足特定一致性标准的历史集。总体原则是，如果历史记录的事务存在严格的总顺序（称为提交顺序，用 $\mathsf{co}$ 表示），则该历史记录满足特定标准，该顺序扩展了写读关系和会话顺序，并且满足某些属性。这些属性由一组公理表示，这些公理将提交顺序与历史记录中的会话顺序和写读关系联系起来。

我们使用的公理具有统一的形式：它们定义了在历史记录中读取的事务 $t_1$ 的强制共同前驱 $t_2$ 。例如，称为读提交（RC）[Berenson et al 1995] 的标准要求历史中读取的每个值都是由提交的事务写入的，而且同一事务中的读取是单调的，因为它们确实不返回较旧的值，w.r.t.提交顺序，而不是过去读取的其他值 4。虽然第一个条件适用于任何历史记录（由于 $\mathsf{wr}$ 的满射性），但第二个条件由图 2a 中的已提交读公理表示。该公理指出，对于写入在事务 $t$ 中读取的变量 $x$ 的任何事务 $t_1$ ，在同一事务中写入 $x$ 并先前读取的事务集 $t_2$ 的提交顺序必须先于 $t_1$ 。例如，图 3a 显示了不满足此公理的历史记录和（部分）提交顺序，因为 $\mathsf{read}(x)$ 返回的事务中写入的值比前一个 $\mathsf{read}(y)$ 中读取的事务更旧。图 3b 给出了满足该公理的历史记录和提交顺序的示例。

更准确地说，这些公理是以下形式的一阶公式（像往常一样，这些公式在历史记录 $h$ 的元组 $⟨h,\mathsf{co}⟩$ 和 $h$ 中事务的提交顺序 $\mathsf{co}$ 上进行解释）：

$$\mathrm{\forall }x,\mathrm{\forall }{t}_1,t_2,\mathrm{\forall }\alpha .t_1\ne t_2\wedge ⟨t_1,\alpha ⟩\in {\mathsf{wr}}_x\wedge t_2\text{ writes }x\wedge \varphi (t_2,\alpha )\Rightarrow ⟨t_2,t_1⟩\in \mathsf{co}$$

其中 $\varphi (t_2,\alpha )$ 是与 $t_2$ 和 $\alpha$（即从 $t_1$ 读取的数据或事务读取）相关的属性，该属性随一个公理的不同而变化。直观上，这个公理模式陈述如下：为了让 $\alpha$ 能够专门读取 $t_1$ 对 $x$ 的写入，必须是每个也写入 $x$ 并满足 $\varphi (t_2,\alpha )$ 的 $t_2$ 在 $t_1$ 之前提交。请注意，在我们考虑的所有情况下， $\varphi (t_2,\alpha )$ 已经确保 $t_2$ 在读取 $\alpha$ 之前提交，因此该公理模式确保 $t_2$ 在 $t_1$ 写入之前进一步提交。

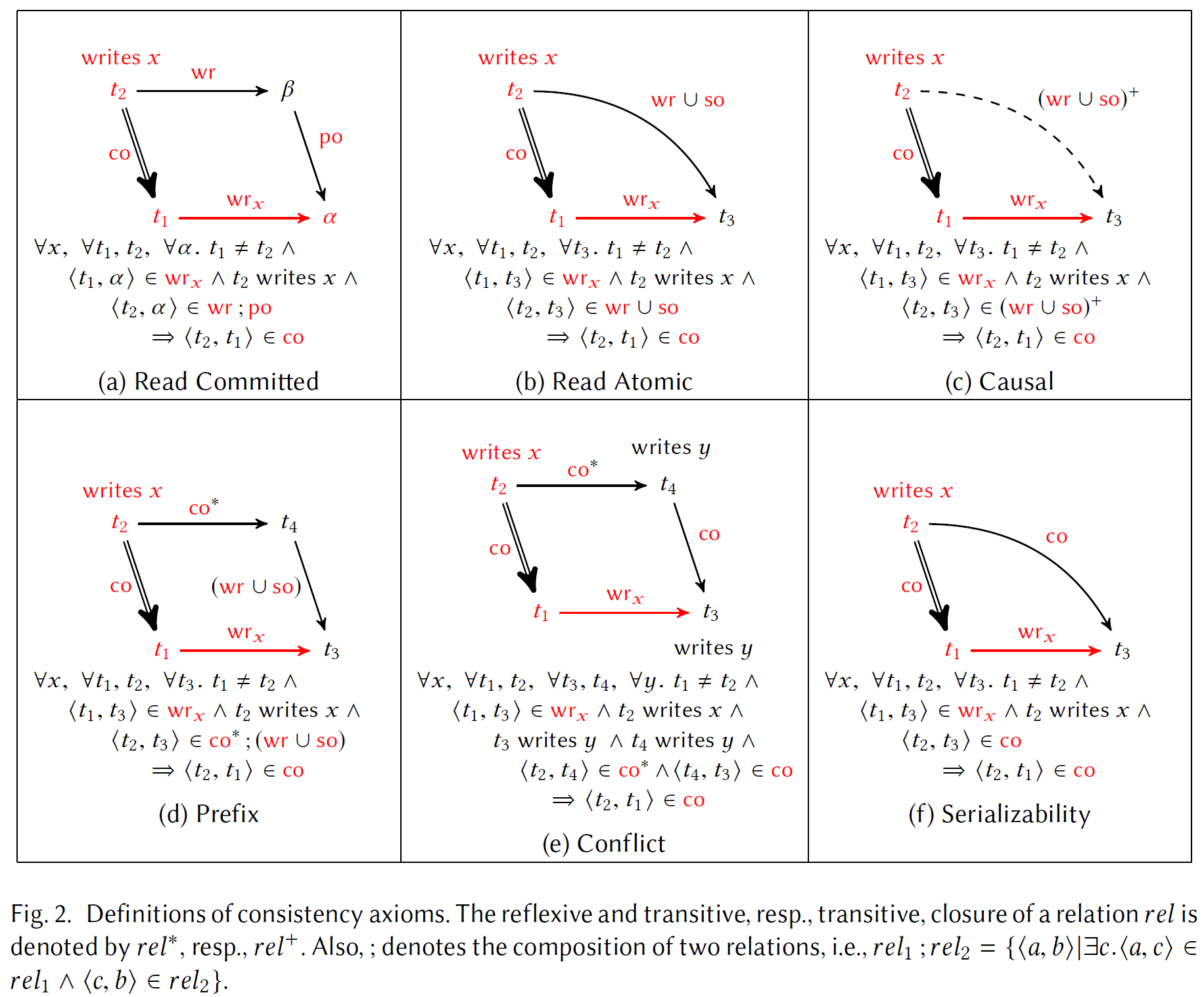
图 2 给出了整篇论文中使用的公理。属性 $\varphi$ 使用写-读关系、历史记录中的会话顺序以及提交顺序将 $t_2$ 和 $\alpha$ 联系起来。

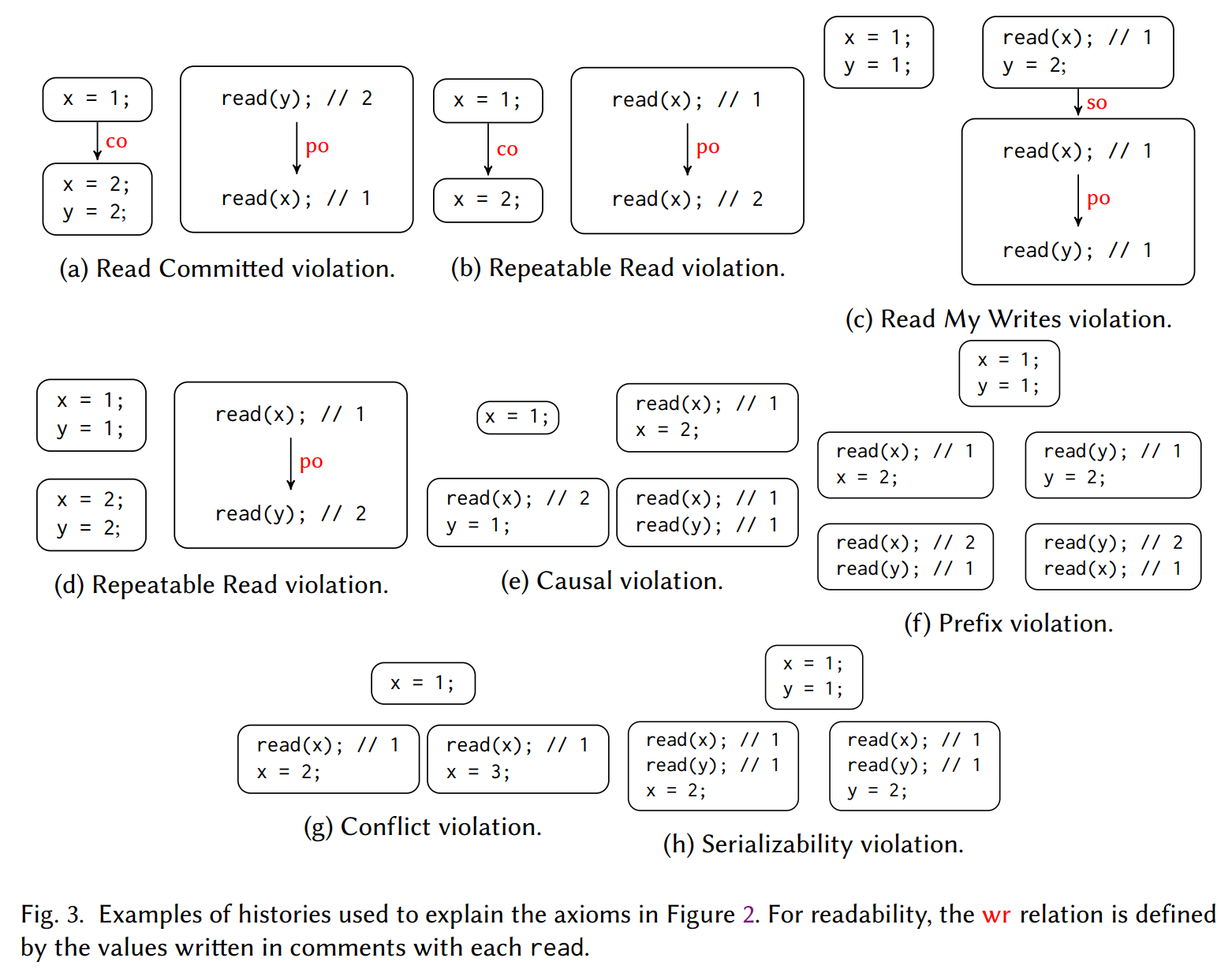
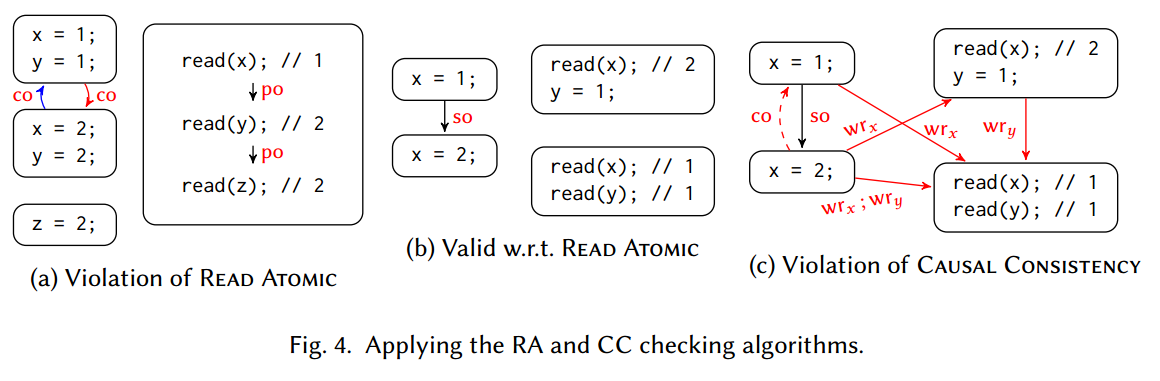
下面，我们解释我们考虑的其余一致性标准以及定义它们的公理。读原子（RA）[Cerone 等人 2015] 是由读原子公理定义的读提交的强化，它规定对于任何事务 $t_1$ 写入在事务 $t_3$ 中读取的变量 $x$，$\mathsf{wr}$ 或 $\mathsf{so}$ 前驱的集合 $t_3$ 中写入 $x$ 的提交顺序必须先于 $t_1$。 $\mathsf{wr}$ 前驱的情况对应于 [Berenson et al 1995] 中的可重复读取标准，该标准要求同一事务中对同一变量的连续读取返回相同的值，图 3b 显示了违规，并且每次读取 $a$ 事务 $t$ 中的变量 $x$ 返回由 $t$ 读取的最大事务 $t^{\prime }$（w.r.t. 提交顺序）写入的值，图 3d 显示了违规（对于左侧事务之间的任何提交顺序， $\mathsf{read}(x)$ 或 $\mathsf{read}(y)$ 将返回一个未由最大事务写入的值）。前驱的情况对应于有关会话的“read-my-writes”保证 [Terry et al 1994]，该保证规定事务 $t$ 必须观察同一会话中先前的写入。例如，图 3c 中的 $\mathsf{read}(y)$ 返回 1 表明右侧的最后一个事务不满足此保证：将 1 写入 $y$ 的事务在将 2 写入 $y$ 之前对该会话已经可见，因此值 2 应该已经读过。Read Atomic 要求读取 $y$ 的事务的 $\mathsf{so}$ 前驱在向 $y$ 写入 1 的事务之前在 $\mathsf{co}$ 中排序，这使得并集 $\mathsf{co}\cup \mathsf{wr}$ 循环。

下面的引理表明，对于满足 Read Atomic 的历史，${\mathsf{wr}}_x$ 的逆扩展到交易是一个总函数（证明见附录 A）。

引理 2.3

设 $h=⟨T,\mathsf{so},\mathsf{wr}⟩$ 是历史。如果 $⟨h,\mathsf{co}⟩$ 满足 Read Atomic，则对于每个事务 $t$ 和两次读取 ${\mathsf{read}}_{i_1}(x,v_1),{\mathsf{read}}_{i_2}(x,v_2)\in \mathsf{reads}(t),{\mathsf{wr}}^{-1}({\mathsf{read}}_{i_1}(x,v_1))={\mathsf{wr}}^{-1}({\mathsf{read}}_{i_2}(x,v_2))$ 且 $v_1=v_2$。

因果一致性（CC）[Lamport 1978] 由因果公理定义，该公理指出，对于任何事务 $t_1$ 写入在事务 $t_3$ 中读取的变量 $x$，$(\mathsf{wr}\cup \mathsf{so}{)}^{+}{t}_3$ 写入 $x$ 的前驱集合必须按提交顺序位于 $t_1$ 之前（$(\mathsf{wr}\cup \mathsf{so}{)}^{+}$ 通常称为因果顺序）。图 3e 中可以发现违反该公理的情况：事务 $t_2$ 将 2 写入 $x$ 是 $(\mathsf{wr}\cup \mathsf{so}{)}^{+}$ 事务 $t_3$ 从 $x$ 读取 $1$ 的前置事务，因为事务 $t_4$ 将 $1$ 写入 $y$，从 $t_2$ 读取 $x$，$t_3$ 从 $t_4$ 读取 $y$。这意味着 $t_2$ 在提交顺序上应该先于事务 $t_1$ 将 $1$ 写入 $x$，这又与写-读关系（$t_2$ 从 $t_1$ 读取）不一致。

前缀一致性（PC）[Burckhardt et al. 2015]是 CC 的加强，它要求每个事务遵守所有事务之间提交顺序的前缀。直觉上观察到的事务是 $\mathsf{wr}\cup \mathsf{so}$ 前驱，定义 PC 的公理前缀指出，对于写入在事务 $t_3$ 中读取的变量 $x$ 的任何事务 $t_1$，由 $t_3$ 写入 $x$ 观察到的事务的 ${\mathsf{co}}^{\ast }$ 前驱集合按提交顺序必须先于 $t_1$（我们使用 ${\mathsf{co}}^{\ast }$ 来表示即使 $t_3$ 观察到的事务也必须先于 $t_1$）。这确保了上述前缀属性。PC 违规的示例可以在图 3f 中找到：底部的两个事务从顶部的三个事务读取，但这三个事务的任何序列化都将意味着 $x=1$、$y=2$ 或在此序列化中，无法在前缀末尾生成 $x=2$，$y=1$。

快照隔离（SI）[Berenson et al. 1995] 是对 PC 的强化，如果两个事务发生冲突，即不允许两个事务观察到相同的提交顺序前缀，即写入公共变量。它是由前缀公理和另一个称为冲突公理的规则结合定义的。冲突公理要求对于任何事务 $t_1$ 写入在事务 $t_3$ 中读取的变量 $x$，在 $t_3$ 之前写入与 $t_3$ 冲突的事务 $x$ 的 ${\mathsf{co}}^{\ast }$ 前驱集合按提交顺序，必须在 $t_1$ 之前。图 $3g$ 显示了冲突违规的情况。

最后，可串行性（SER）[Papadimitriou 1979] 由同名公理定义，它要求对于任何写入事务 $t_3$ 中读取的变量 $x$ 的事务 $t_1$，$t_3$ 写入 $x$ 的共同前驱集合必须按提交顺序位于 $t_1$ 之前。这确保了每笔交易都能观察到所有共同前任交易的影响。图 3h 显示了可串行性违规的情况。

下一个引理说明了这些公理之间的关系（参见附录 A 的证明）。

引理 2.4 以下蕴涵成立：

$$\begin{gathered} \text{Causal}\Rightarrow \text{Read Atomic}\Rightarrow \text{Read Committed}\text{ \\ Prefix⇒Causal \\ Serializability⇒Prefix∧Conflict} \end{gathered}$$

CHECKING CONSISTENCY CRITERIA

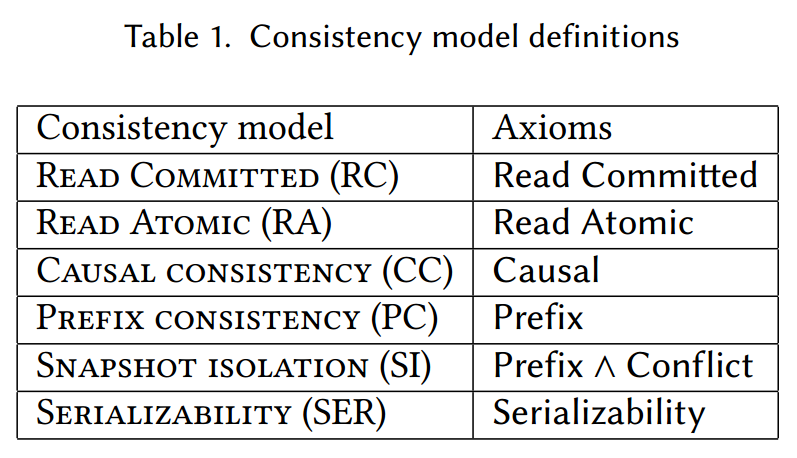
本节确定了针对给定历史记录检查表 1 中不同一致性标准的复杂性。更准确地说，我们表明可以在多项式时间内检查已提交读、原子读和因果一致性，而检查其余标准的问题是 NP 完全的。

直观上，多项式时间结果基于以下事实：定义这些一致性标准的公理不包含蕴涵左侧的提交顺序 ($\mathsf{co}$)。因此，证明满足这些公理的提交顺序的存在可以使用饱和过程来完成，该饱和过程基于实例化给定历史中的写-读关系和会话顺序的公理来构建“部分”提交顺序。由于提交顺序必须是写读关系和会话顺序的扩展，因此它从一开始就包含这两个关系。当以这种方式导出的阶次约束变成循环时，该饱和过程停止。例如，让我们考虑对图 4a 和图 4b 中的历史应用与 RA 相对应的程序。将图 2b 中的公理应用于第一个历史记录，由于右侧的事务从 y 读取 2，我们得到它的 ${\mathsf{wr}}_x$ 前驱（即左侧的第一个事务）必须先于按提交顺序将 2 写入 y 的事务（红边）。这是成立的，因为 ${\mathsf{wr}}_x$ 前驱写在 y 上。类似地，由于同一个事务从 x 读取 1，我们知道它的前驱事务必须先于按提交顺序向 x 写入 1 的事务（蓝色边缘）。这已经暗示了循环提交顺序，因此，该历史记录不满足 RA。另一方面，对于图 4b 中的历史，所有公理实例化都是空的，即蕴涵的左边部分是假的，因此，它满足 RA。检查图 4c 中历史记录的 CC 需要一个饱和步骤：由于右下角的事务从 x 读取 1，这是 ${\mathsf{wr}}_x$ ；在 x 上写入的 ${\mathsf{wr}}_y$ 前驱（左下角的事务）在提交顺序中必须先于向 x 写入 1 的事务（图中 ${\mathsf{wr}}_x;{\mathsf{wr}}_y$ 表示 ${\mathsf{wr}}_x\circ {\mathsf{wr}}_y$，对应的箭头应该是虚线）。由于这已经与会话顺序不一致，我们得知该历史记录违反了 CC。

算法 1 列出了我们检查 CC 的过程。如上所述，$\mathsf{co}$ 最初设置为 $\mathsf{so}\cup \mathsf{wr}$，然后，它被公理 Causal 的非空实例化所隐含的其他排序约束所饱和（其中蕴涵的左侧计算结果为 true）。有关 RC 和 RA 的算法以类似的方式定义，通过本质上更改第 6 行的测试，使其对应于相应公理中蕴涵的左侧。算法 1 可以重写为 Datalog 程序，其中包含用于计算传递闭包和关系组合的简单 Datalog 规则，以及形式化的规则：

TODO

来表示因果公理。以下是这些算法在多项式时间内运行的结果（或者等效地，可以在包含给定历史中的 $\mathsf{wr}$ 和 $\mathsf{so}$ 关系的数据库上以多项式时间评估相应的 Datalog 程序）。

定理 3.1. 对于任何标准 $C\in \{\mathsf{RC},\mathsf{RA},\mathsf{CC}\}$，检查给定历史是否满足 C 的问题是多项式时间。

另一方面，检查 PC、SI 和 SER 通常是 NP 完全的。我们使用布尔可满足性（SAT）的减少来展示这一点，该减少统一覆盖了所有三种情况。就 SER 而言，Papadimitriou [1979] 提供了 的 NP 完整性结果的新证明，该证明使用了所谓的非循环 SAT 的约简，并且不能扩展到 PC 和 SI。

定理 3.2. 对于任何准则 $C\in \{\mathsf{PC},\mathsf{SI},\mathsf{SER}\}$，检查给定历史是否满足 C 的问题是 NP 完全的。

证明：TODO

CHECKING CONSISTENCY OF BOUNDED-WIDTH HISTORIES

在本节中，我们将展示在给定历史记录的宽度（即相互无序事务的最大数量）的假设下，检查前缀一致性、快照隔离和可串行性变成了多项式时间。会话顺序受固定常数限制。如果我们考虑会话顺序是事务序列的并集（以写入初始值的虚构事务为模）的标准情况，即一组会话，那么历史的宽度就是会话的数量。我们首先提出一种用于检查可串行性的算法，该算法是当宽度受固定常数限制时的多项式时间。一般来说，该算法的渐近复杂度在历史宽度上是指数级的，但这种最坏情况的行为在实践中并没有被执行，如第 6 节所示。然后，我们证明可以减少检查前缀一致性和快照隔离检查可串行性问题的多项式时间。

Checking Serializability

我们提出了一种用于检查给定历史记录的可序列化性的算法，该算法通过按照与会话顺序一致的顺序逐一“线性化”事务来构造有效的提交顺序（满足序列化）（如果有）。在任何时候，已经线性化的事务集都由会话顺序的反链唯一确定（即，一组相互无序的事务 w.r.t. $\mathsf{so}$），并且下一个要线性化的事务是在事务的直接后继者中选择的在这个反链中。该算法的关键在于，可以选择下一个要线性化的事务，以便它不会以不依赖于已线性化事务之间的顺序的方式产生串行化违规。因此，该算法可以看作是在 $\mathsf{so}$ 反链空间中的搜索。如果历史的宽度有界（由固定常数），则可能的反链数量是历史大小的多项式，这意味着搜索可以在多项式时间内完成。

历史 $h=⟨T,\mathsf{so},\mathsf{wr}⟩$ 的前缀是一组事务 $T^{\prime }\subseteq T$，使得 $T^{\prime }$ 中的所有 $\mathsf{so}$ 前驱事务也在 $T^{\prime }$ 中，即 $\mathrm{\forall }t\in T,{\mathsf{so}}^{-1}(t)\in T^{\prime }$。前缀 $T^{\prime }$ 由 $T^{\prime }$ 中关于 $\mathsf{so}$ 最大的事务集唯一确定。这组事务形成了一个反链，即该组中的任何两个元素对于 $\mathsf{so}$ 都是不可比较的。给定一个反链 $\{t_1,\dots ,t_n\}$，我们可以说 $\{t_1,\dots ,t_n\}$ 是前缀 $T^{\prime }=\{t:\mathrm{\exists }i,⟨t,t_i⟩\in \mathsf{so}\vee t=t_i\}$ 的边界。例如，给定图 6a 中的历史记录，事务集 $\{t_0,t_1,t_2\}$ 是具有边界 $\{t_1,t_2\}$ 的前缀（后者是会话顺序的反链）。

历史 $h$ 的前缀 $T^{\prime }$ 被称为可序列化，当且仅当 $h$ 中的事务存在部分提交顺序 $\mathsf{co}$ 使得以下内容成立：

• $\mathsf{co}$ 与 $h$ 中的会话顺序和写-读关系不矛盾，即 $\mathsf{wr}\cup \mathsf{so}\cup \mathsf{co}$ 是无环的；
• $\mathsf{co}$ 是 $T^{\prime }$ 中事务的全序；
• $\mathsf{co}$ 将 $T^{\prime }$ 中的事务排序在 $T\setminus T^{\prime }$ 中的事务之前，即对于每个 $t_1\in T^{\prime },t_2\in T\setminus T^{\prime }$，$⟨t_1,t_2⟩\in \mathsf{co}$；
• $\mathsf{co}$ 不会对任何两个事务 $t_1,t_2\notin T^{\prime }$ 进行排序；
• 历史记录 $h$ 以及提交顺序 $\mathsf{co}$ 满足定义可串行性的公理，即 $⟨h,\mathsf{co}⟩\models \mathsf{Serialization}$。

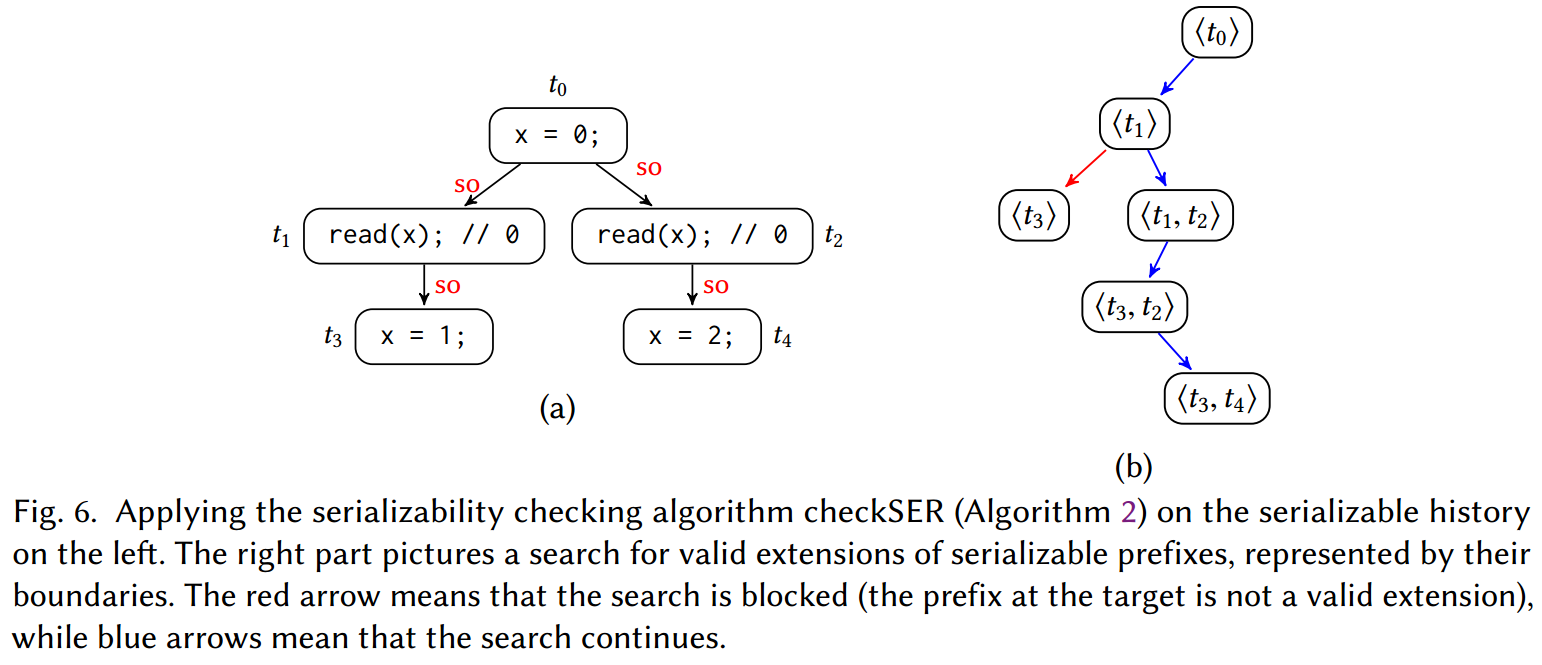
对于图 6a 中的历史记录，前缀 $\{t_0,t_1,t_2\}$ 是可序列化的，因为存在一个部分提交顺序 $\mathsf{co}$，它按照此顺序排列 $t_0,t_1,t_2$，并且 $t_1$ 和 $t_2$ 都在 $t_3$ 和 $t_4$ 之前。公理序列化很容易满足，因为前缀包含写入 $x$ 的单个事务，并且前缀之外的所有事务都不读取 $x$。

$h$ 的前缀 $T^{\prime }\uplus t$ 被称为 $h$ 的可序列化前缀 $T^{\prime }$ 的有效扩展，表示为 $T^{\prime }▹T^{\prime }\uplus t$，如果满足以下条件：

• $t$ 不从 $T^{\prime }$ 之外的事务读取，即对于每个 $t^{\prime }\in T\setminus T^{\prime }$，$⟨t^{\prime },t⟩\notin \mathsf{wr}$。
• 对于 $t$ 写入的每个变量 $x$，在 $T^{\prime }$ 之外不存在事务 $t_2\ne t$ 读取由 $t_1\in T^{\prime }$ 写入的 $x$ 值，即对于每个 $x$ 和每个 $t_1\in T^{\prime }$，$t_2\in T\setminus (T^{\prime }\uplus t)$，$⟨t_1,t_2⟩\notin \mathsf{wr}$。（原文如此，笔者认为此处应该改为 $⟨t_1,t_2⟩\notin {\mathsf{wr}}_x$）

对于图 6a 中的历史记录，我们有 $\{t_0,t_1\}▹\{t_0,t_1\}\uplus \{t_2\}$，因为 $t_2$ 从 $t_0$ 读取并且不写入任何变量。另一方面，$\{t_0,t_1\}\mathrm{not}▹\{t_0,t_1\}\uplus \{t_3\}$，因为 $t_3$ 写入 $x$，而在此前缀之外的事务 $t_2$ 从前缀中包含的事务 $t_0$ 读取。

令 ${▹}^{\ast }$ 表示 $▹$ 的自反和传递闭包。

以下引理对于证明初始空前缀的迭代有效扩展可用于表明给定历史是可序列化的至关重要。

引理 4.1 对于历史 $h$ 的可序列化前缀 $T^{\prime }$，如果前缀 $T^{\prime }\uplus t$ 是 $T^{\prime }$ 的有效扩展，则扩展后的前缀是可序列化的。

证明 令 ${\mathsf{co}}^{\prime }$ 为满足可序列化前缀条件的 $T^{\prime }$ 的部分提交顺序。我们将 ${\mathsf{co}}^{\prime }$ 扩展到偏序 $\mathsf{co}={\mathsf{co}}^{\prime }\cup \{⟨t,t^{\prime }⟩|t^{\prime }\notin T^{\prime }\uplus \{t^{\prime }\}\}$。我们证明 $⟨h,\mathsf{co}⟩\models \mathsf{Serialization}$。$T^{\prime }\uplus \{t\}$ 是可序列化前缀的其他条件可以通过 $\mathsf{co}$ 轻松满足。

TODO

算法 2 列出了我们用于检查可串行性的算法。它被定义为一个递归过程，搜索给定前缀的有效扩展序列（最初，该前缀为空），直到覆盖整个历史记录。图 6b 描绘了图 6a 中历史记录的搜索情况。右侧分支（包含蓝色边缘）仅包含有效扩展，并且它到达包含历史记录中所有事务的前缀。

定理 4.2 历史 $h$ 是可序列化的当且仅当 $\mathsf{checkSER}(h,\mathrm{\varnothing })$ 返回 true。

证明 TODO

算法 2 枚举给定历史 $h$ 的前缀，每个前缀由包含该前缀中最大事务的 $h$ 的反链唯一确定。根据定义，历史 $h$ 的每个反链的大小小于 $h$ 的宽度。因此，历史 $h$ 的可能反链（前缀）的数量为 $O(\mathsf{size}(h{)}^{\mathsf{width}(h)})$，其中 $\mathsf{size}(h)$、$\mathsf{width}(h)$ 分别是事务数量、宽度，$h$。由于可以在二次时间内检查有效扩展属性，因此由 $\mathsf{checkSER}$ 定义的算法的渐近时间复杂度上限为 $O(\mathsf{size}(h{)}^{\mathsf{width}(h)}\cdot \mathsf{size}(h{)}^3)$。以下推论是这些观察的直接结果。

推论 4.3 对于任意但固定的常数 $k\in \mathbb{N}$，检查宽度至多为 k 的历史的可串行性的问题是多项式时间。

Reducing Prefix Consistency to Serializability

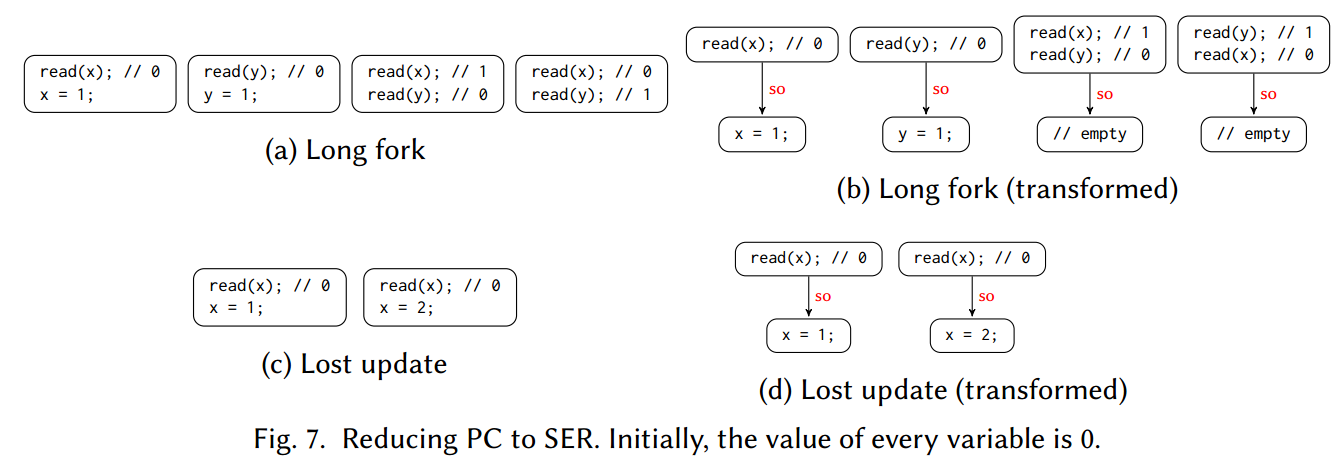
定理 4.8 历史 $h$ 满足前缀一致性当且仅当 $h_{R|W}$ 是可序列化的

推论 4.9 对于任意但固定的常数 $k\in \mathbb{N}$，检查宽度至多为 k 的历史的前缀一致性的问题是多项式时间。

Reducing Snapshot Isolation to Serializability

定理 4.10 历史 $h$ 满足 SI 当且仅当 $h_{R|W}^c$ 是可序列化的

COMMUNICATION GRAPHS

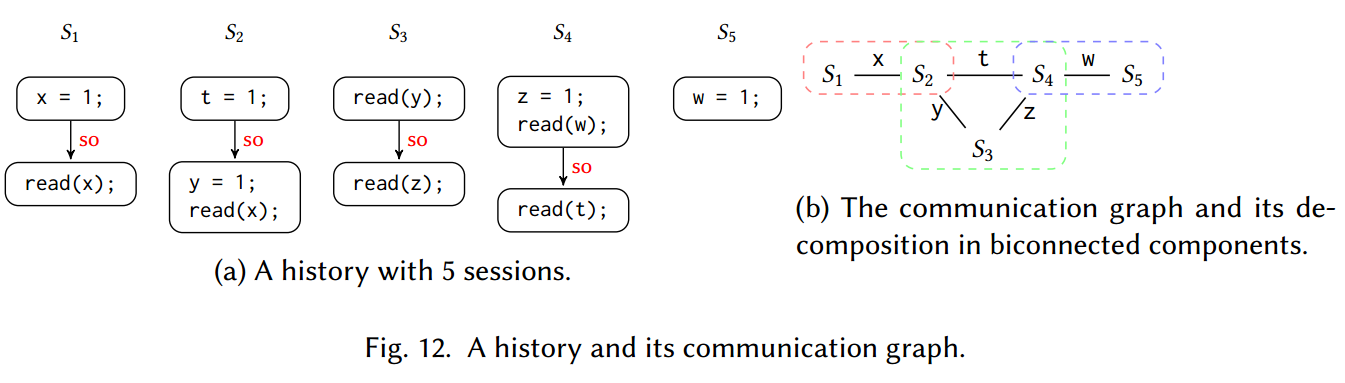
在本节中，我们提出了 PC、SI 和 SER 多项式时间结果的扩展，它允许处理不同会话之间共享变量稀疏的历史。对于本节的结果，我们采取简化的假设，即会话顺序是事务序列的并集（以写入初始值的虚构事务为模），即每个事务序列对应于会话的标准概念。我们使用称为通信图的无向图来表示不同会话之间的变量共享。例如，图 12a 中的历史通信图在图 12b 中给出。为了便于阅读，在边上标记了两个会话访问的变量。

我们证明，当通信图的每个双连通分量的大小受固定常数限制时，检查 PC、SI 或 SER 的问题是多项式时间。这比第 4 节中的结果更强，因为双连通分量的数量可以任意大，这意味着会话总数是无限的。一般来说，我们证明这些一致性标准的时间复杂度仅在此类双连通分量的最大大小中呈指数增长，而不是在会话总数中呈指数增长。

一个无向图是双连通的，意味着它是连通的，并且如果要删除任何一个顶点，该图将保持连通状态，并且图 $G$ 的双连通分量是 $G$ 的最大双连通子图。图 12b 显示了通信图双连通分量的分解。该图包含 5 个会话，而每个双连通分量的大小最多为 3。直观上，如果历史 $h$ 违反了某些一致性标准 $C\in \{\mathsf{PC},\mathsf{SI},\mathsf{SER}\}$，则存在来自同一双连通分量的会话上的 $h$ 投影，这也违反了 $C$（反之亦然） 。因此，可以针对每个双连通分量（更准确地说，在仅包含同一双连通分量中的会话的子历史记录上）单独检查这些标准中的任何一个。实际上，这个分解论证甚至适用于 RC、RA 和 CC。例如，在图 12a 中的历史情况中，可以单独查看三个子历史来检查任何一致性标准：具有 $S1$ 和 $S2$ 的子历史，具有 $S2$、$S3$ 和 $S4$ 的子历史，以及 $S4$ 和 $S5$ 的子历史记录。

形式上，历史 $h$ 的通信图是一个无向图 $\mathsf{Comm}(h)=(V,E)$，其中顶点集 $V$ 是 $h$ 中会话的集合，并且 $(v,v^{\prime })\in E$ 当且仅当会话 $v$ 和 $v^{\prime }$ 分别包含两个事务 $t_1$ 和 $t_2$，使得 $t_1$ 和 $t_2$ 读取或写入公共变量 $x$。

我们从一个技术引理开始，表明图中表示历史 $h$ 和关系 $\mathsf{co}$（在 $h$ 的交易上）的某种形式的最小路径位于底层通信图的单个双连通分量内。这用于表明任何一致性违规都可以通过一次查看单个双连通分量来暴露。表示历史 $h$ 和关于 $h$ 的交易的关系 $\mathsf{co}$ 的图由 $G(h,\mathsf{co})$ 表示。

给定图 $G(h,\mathsf{co})$ 和其顶点上的关系 $r$，关系 $\mathsf{so},\mathsf{wr}$ 和 $\mathsf{po}$ 上的项，例如 $(\mathsf{wr}\cup \mathsf{so}{)}^{+}$，形式为 $r$ 的路径（或 $r$ 路径）是表示由项 $r$ 指定的 $\mathsf{so},\mathsf{wr}$ 或 $\mathsf{co}$ 依赖关系的边序列，例如 $\mathsf{wr}$ 或 $\mathsf{so}$ 依赖关系的序列。

TODO

EXPERIMENTAL EVALUATION

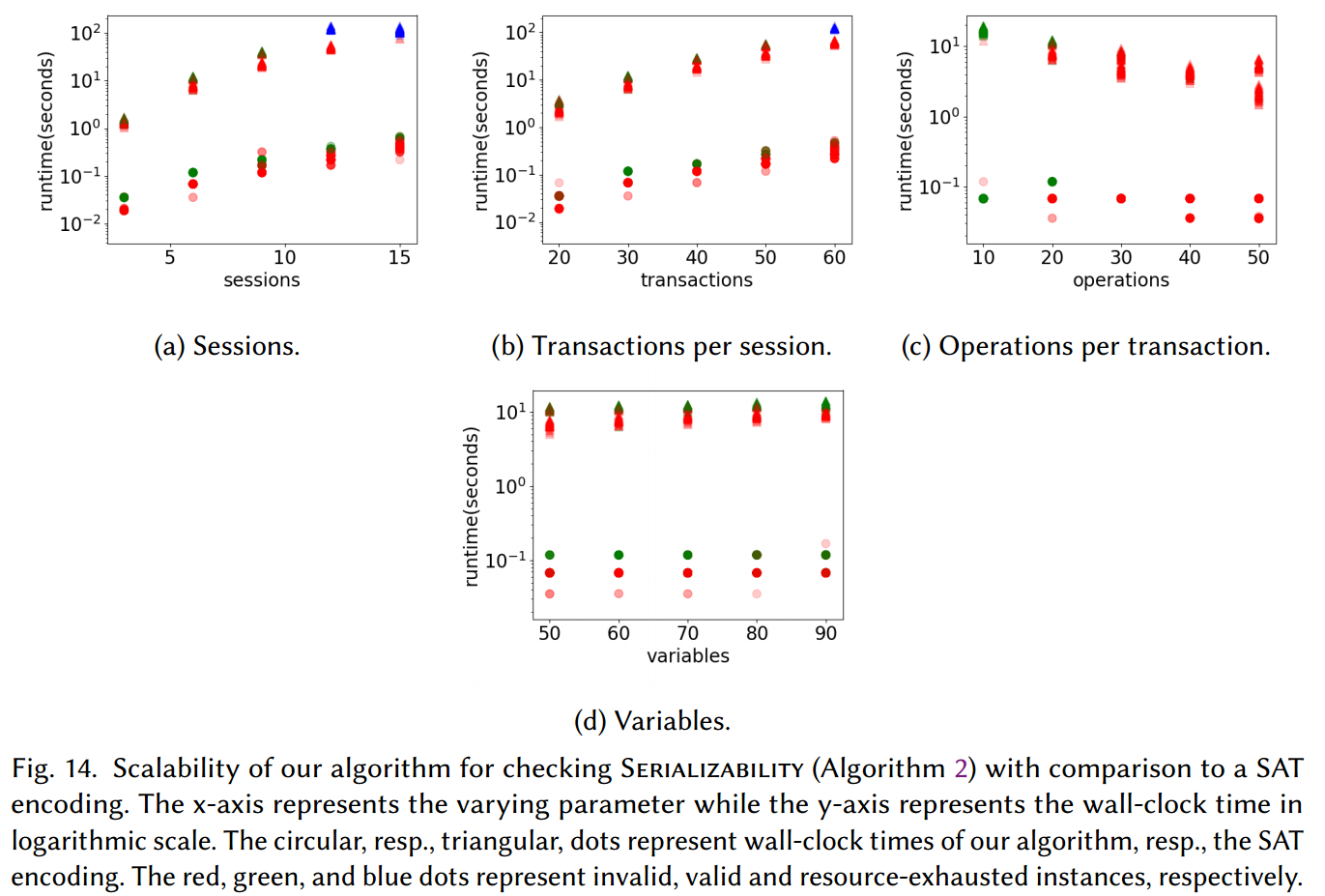
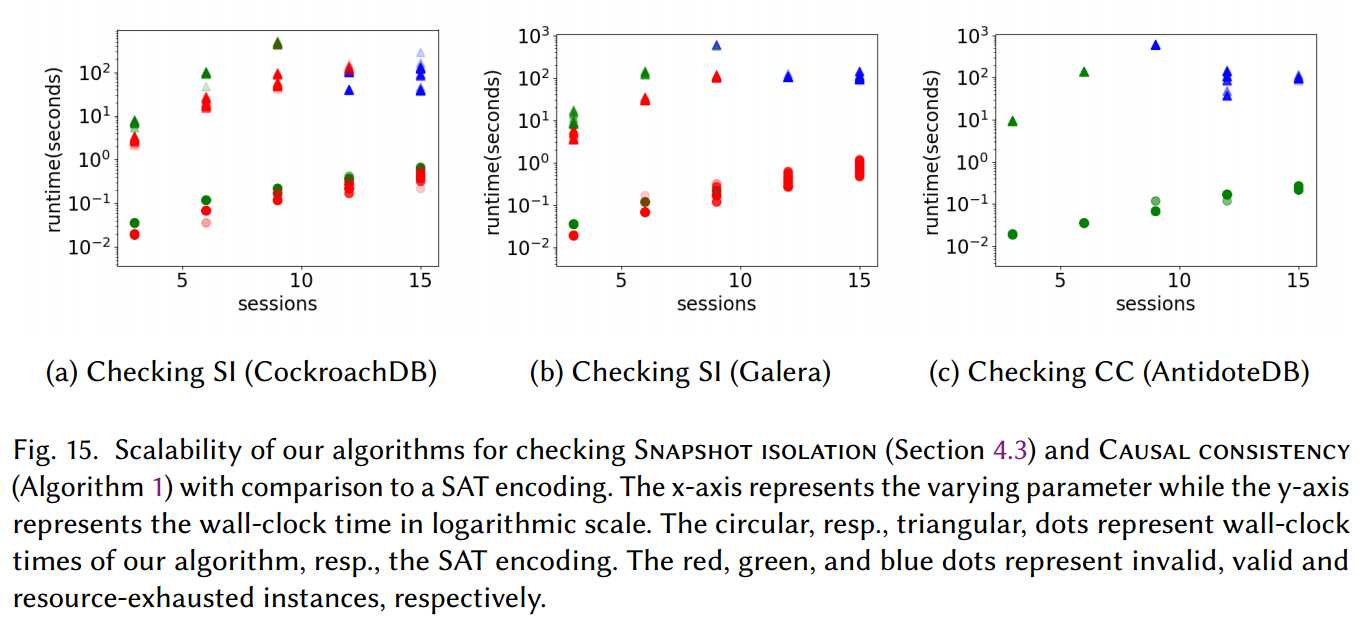
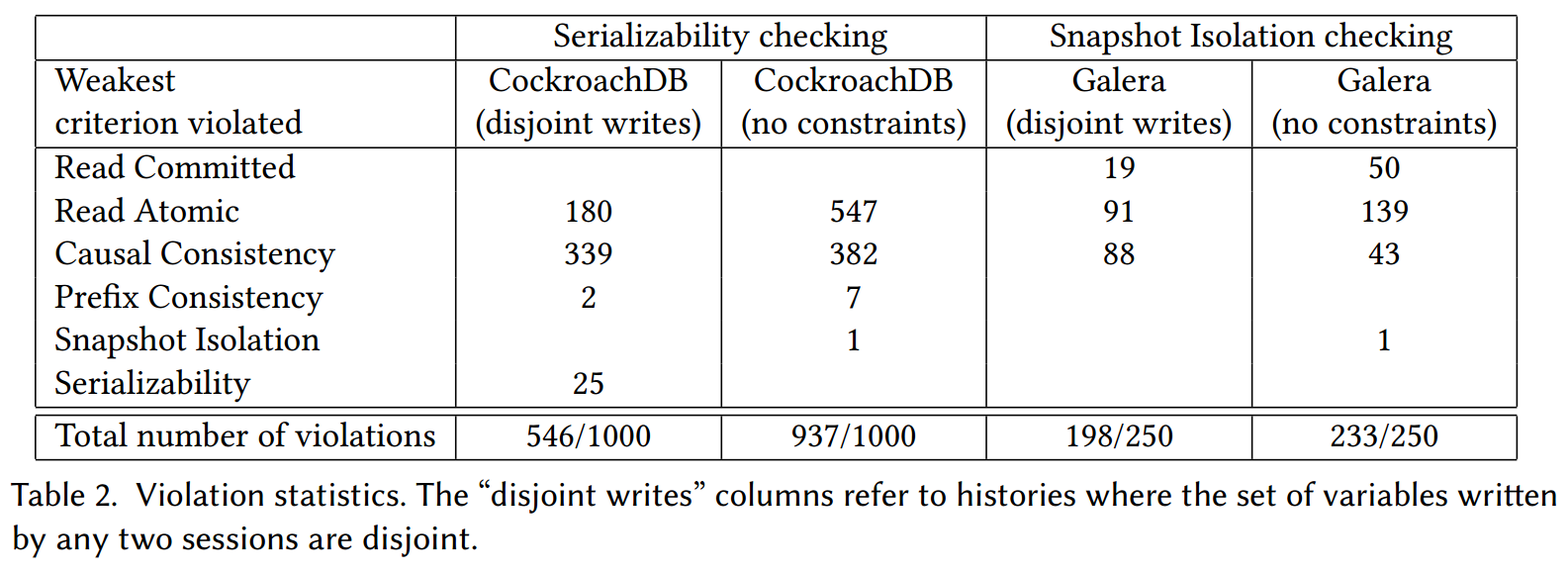
RELATED WORK

Cerone 等人 [2015] 使用 Burckhardt 等人 [2014] 的规范方法，对我们在本文中考虑的标准进行了首次形式化。这种形式化使用两个辅助关系，一个是可见性关系，它表示一个事务“观察”另一个事务的影响，另一个是提交顺序，也称为仲裁顺序，就像我们的例子一样。使用仅包括会话顺序的历史概念来抽象执行，并且对某些一致性标准的遵守被定义为存在可见性关系和满足某些公理的提交顺序。在实际目标的推动下，我们的历史包括写入-读取关系，这使得能够更统一且在我们看来更直观的公理来描述一致性标准。然而，我们的形式化与 Cerone 等人 [2015] 的形式化是等效的（本文的扩展版本中提出了这种等效性的形式证明 [Biswas 和 Enea 2019]）。此外，Cerone 等人 [2015] 并没有像我们的论文那样研究算法问题。

Papadimitriou [1979] 表明检查执行的可串行性是 NP 完全的。此外，它还确定了一个更强的标准，称为冲突可串行性，它是多项式时间可检查的。冲突可串行性假设历史作为操作序列给出，并要求提交顺序与基于该序列定义的事务之间的冲突顺序一致（粗略地说，如果事务 $t_1$ 在 $t_2$ 之前访问某个变量 $x$，则事务 $t_1$ 按冲突顺序位于事务 $t_2$ 之前）。此结果不适用于分布式数据库，在分布式数据库中，不可能在提交到网络中不同节点的操作之间得出这样的序列。

Bouajjani 等人[2017] 表明，检查非事务性分布式数据库执行中因果一致性的几种变化需要多项式时间（他们还假设每个值最多写入一次）。假设单例事务，我们的 CC 概念对应于 Bouajjani 等人 [2017] 中的因果收敛标准。因此，我们关于 CC 的结果可以看作是关于因果收敛到事务的结果的延伸。

有一些工作研究了检查共享内存系统中的一致性标准（例如顺序一致性和线性化）的问题。 Gibbons 和 Korach [1997] 表明，检查单值寄存器类型的线性化能力一般来说是 NP 完全的，但执行时需要多项式时间，其中每个值最多写入一次。通过减少可串行性，他们表明即使每个值最多写入一次，检查顺序一致性也是 NP 完全的。 Emmi 和 Enea [2018] 将有关线性化的结果扩展到一系列称为集合的抽象数据类型，其中包括堆栈、队列、键值映射等。顺序一致性简化为具有单例事务的历史的可串行性（即，由单个读或写操作）。因此，我们用于检查有界宽度历史的可串行性的多项式时间结果（推论 4.3）意味着用有界数量的线程检查历史的顺序一致性是多项式时间。后一个结果是由 Abdulla 等人独立建立的[2019]。

通信图的概念受到 Chalupa 等人 [2018] 的工作的启发，该工作研究了多线程程序的偏序约简（POR）技术。一般来说，偏序约简的目标 [Flanagan and Godefroid 2005] 是避免探索对于一些合适的等价概念等价的执行，例如 Mazurkiewicz 迹等价 [Mazurkiewicz 1986]。他们使用通信图的非循环性来定义其 POR 技术最适合的一类程序。他们探索的算法问题与我们的不同，并且他们不像我们的结果那样研究该图的双连通分量。

CONCLUSIONS

我们的结果提供了一种有效的方法，以有效的方式检查事务数据库在广泛的一致性标准方面的正确性。我们为这些标准设计了一个新的规范框架，除了启用有效的验证算法之外，还提供了对它们之间在执行期间读取的事务之前必须提交的事务集方面的差异的新颖理解。这些算法被证明是可扩展的，并且比这些标准的标准 SAT 编码（如我们的框架中定义的）效率高几个数量级。虽然这些算法非常容易理解和实现，但其正确性的证明并非易事，并且可以从新的规范框架中受益匪浅。

未来工作的一个重要场所是确定特定违规行为的根本原因。事实上，我们能够处理广泛的标准，这已经有助于识别给定执行中违反的最弱标准。然后，在 RC、RA 和 CC 的情况下，不一致对应于提交顺序中的周期，根本原因可以归因于这种关系中的最小周期。我们在与 Antidote 开发人员的沟通中这样做是为了简化我们发现的包含 42 笔事务的违规行为。在 PC、SI 和 SER 的情况下，可以在 SAT 求解器中实现类似于 CDCL 的搜索过程，以便计算根本原因，因为 SAT 求解器将计算不可满足性核心。