题目背景
一个简单的问题,什么是递推?
题目描述
定义一个数列 $\set{a_0 \dots a_{n - 1} }$ 的递推式为满足下式的序列 $\set{r_0\dots r_m}$:
$$ \sum_{j = 0} ^ m r_j a_{i - j} = 0, \forall i \ge m $$
$m$ 称为该递推式的阶数。特别地,$r_0\neq 0$。
给你一个无限长的数列 $\set{a_i}$ 的前 $n$ 项以及数列 $\set{a_i}$ 的一个阶数为 $n$ 的递推式 $\set{b_i}$。
要求求出数列 $\set{a_i}$ 的所有项之和。答案对 $998244353$ 取模。
可以证明,对于任意一个模 $998244353$ 意义下输入,都存在实数意义下的一个对应数列的答案是收敛的。
输入格式
第一行一个正整数 $n$。
第二行输入 $n$ 个整数,表示序列 $\set{a_i}$ 的前 $n$ 项即 $\set{a_0 \dots a_{n-1}}$ 在模 $998244353$ 意义下的值。
第三行输入 $n+1$ 个整数,表示递推式 $\set{b_0\dots b_n}$ 在模 $998244353$ 意义下的值。
输出格式
输出一行一个整数,表示数列 $\set{a_i}$ 的所有项之和对 $998244353$ 取模的结果。
保证答案可以在模 $998244353$ 意义下表示,即如果最终的答案为分数 $\frac qp$(可以证明答案肯定是一个有理数),保证 $p\not\equiv0\pmod {998244353}$。
输入输出样例 #1
输入 #1
1 | |
输出 #1
1 | |
输入输出样例 #2
输入 #2
1 | |
输出 #2
1 | |
输入输出样例 #3
输入 #3
1 | |
输出 #3
1 | |
说明/提示
样例解释 #1
$499122176\equiv -\frac12\pmod {998244353}$。
$\forall i\ge n,a_i-\frac12\times a_{i-1}=0$ 即 $a_i=\frac12\times a_{i-1}$,即数列 $\set{a_i}$ 是等比数列 $1,\frac12,\frac14,\dots$。其和收敛于 $2$。
样例解释 #2
$199648870\equiv -0.6\pmod {998244353},99824435\equiv -0.3\pmod {998244353}$。
$\forall i\ge n,a_i-0.6\times a_{i-1}-0.3\times a_{i-2}=0$ 即 $a_i=0.6\times a_{i-1}+0.3\times a_{i-2}$。经计算,其和收敛于 $14$。
本题使用子任务捆绑/依赖
对于所有子任务,$1\le n\le5\times 10^3$, $0\le a_i,b_i< 998244353$。特别地,$b_0\neq 0$。
| 子任务编号 | 分值 | $n\le$ | 依赖 |
|---|---|---|---|
| $1$ | $30$ | $1$ | 无 |
| $2$ | $30$ | $2$ | $1$ |
| $3$ | $40$ | $5\times 10^3$ | $1,2$ |
题解
将序列 $a$ 写成生成函数:
$$ F(x) = \sum_{i=0}^{+\infty} a_i x^i $$
根据题面给出的递推式:
$$ \sum_{j=0}^{n} b_j a_{i-j} = 0, \quad \forall i \ge n $$
可以得出一个经典构造。以 $n = 3$ 为例:
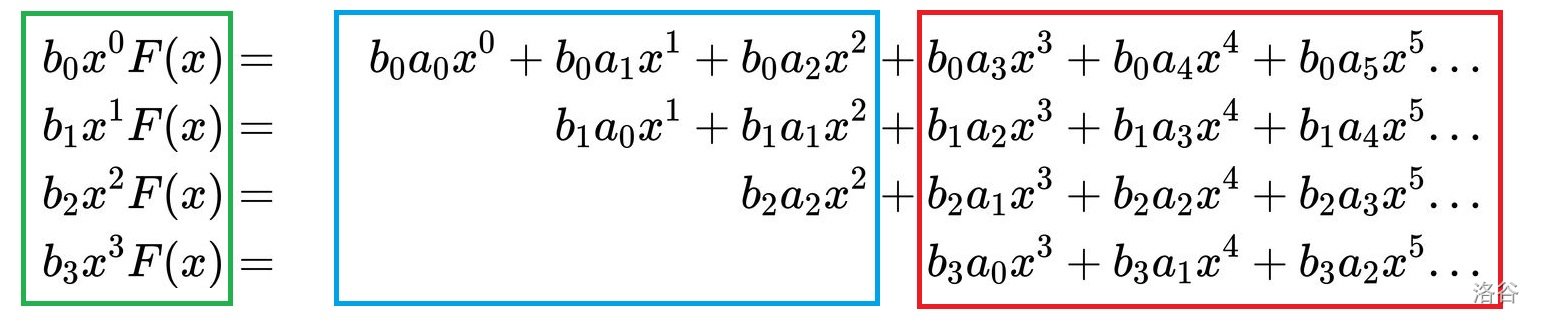
由递推式,红色部分(即每列 $x^k$ 中 $k \geq n$ 的系数项)的和均为 0。因此,绿色部分(等式左边低阶项的和)等于蓝色部分(截断有限和)的和。即:
$$ \sum_{i=0}^{n} b_i x^i \times F(x) = \sum_{i=0}^{n-1} \sum_{j=0}^{n-i-1} b_i a_j x^{i+j} $$
将 $\sum_{i=0}^{n} b_i x^i$ 除到右边即可得到 $F(x)$ 的封闭式。
本题要求 $S = \sum_{i=0}^{+\infty} a_i$。发现 $S = F(1)$,直接代入 $x = 1$ 计算:
$$ S = F(1) $$
使用前缀和优化右侧求和过程,时间复杂度为 $O(n)$。

